In this article, we will study what is a divide and conquer algorithm and will also go through the examples and their python code with output. And lastly, we will learn the advantages, disadvantages, and applications of the divide and conquer algorithm. So, let's get started!
What is a Divide and Conquer Algorithm?
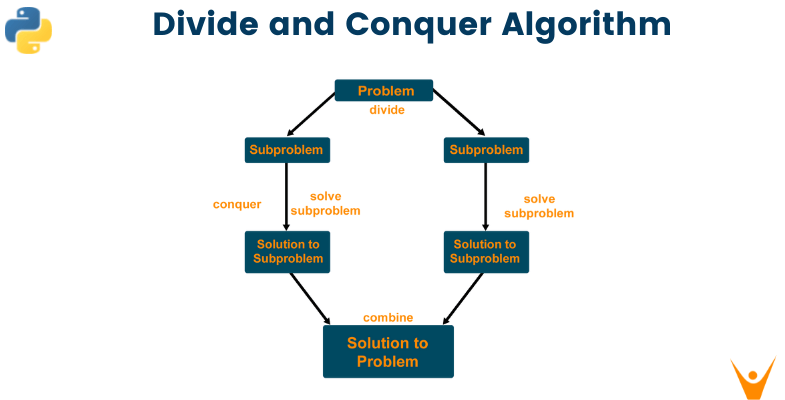
Many useful algorithms are recursive in structure, i.e., to solve the given problem, they call themselves recursively one or more times to deal with closely related sub-problems. These algorithms typically follow a divide-and-conquer algorithm. The divide and conquer algorithm involves three steps at each level of recursion.
- Divide: Break the problem into several sub-problems that are similar to the original problem but smaller,
- Conquer: Solve the sub-problem recursively, and if the sub-problem sizes are small enough, just straightforwardly solve the sub-problems.
- Combine: Combine this solution to create a solution to the original problem
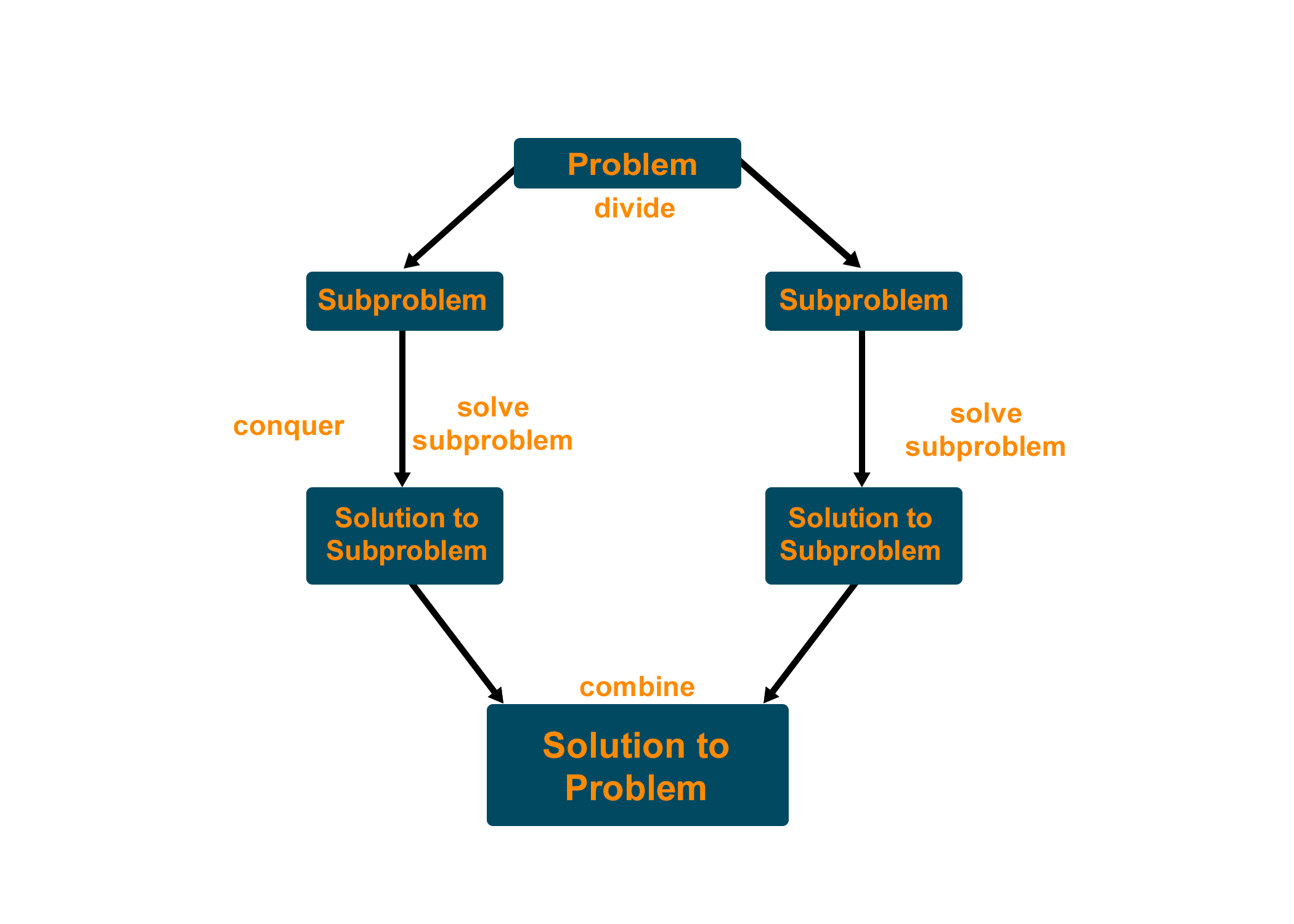
Algorithm Of Divide and Conquer
Consider an arbitrary problem, and let adhoc be a simple algorithm capable of solving the problem. We call adhoc a basic sub-algorithm such that it can be efficient in solving small instances, but its performance on large instances is of no concern.
DivideAndConquer(a, m, n)
{
if(subProblem(a, m, n))
return(solution(a, m, n))
else
p = divide(a, m, n)
b = DivideAndConquer(a, m, mid)
c = DivideAndConquer(a, mid+1, n)
d = combine(b, c)
return(d)
}
Time Complexity
The time complexity for the divide and conquer algorithm is calculated using the master theorem.
T(n) = aT(n/b) + f(n),
where 'n' is the input size, 'a' is the number of sub-problems in the recursion, and ‘n/b’ is the size of each sub-problem where all sub-problems are assumed to have the same size. We can say that f(n) is the work done outside the recursive call.
Divide and Conquer Algorithm Examples
Divide and conquer approach is widely used to solve many problem statements like merge Sort, quick sort, finding closest pair of points, etc. Below we have mentioned 2 such examples which are most important for any programmer to learn.
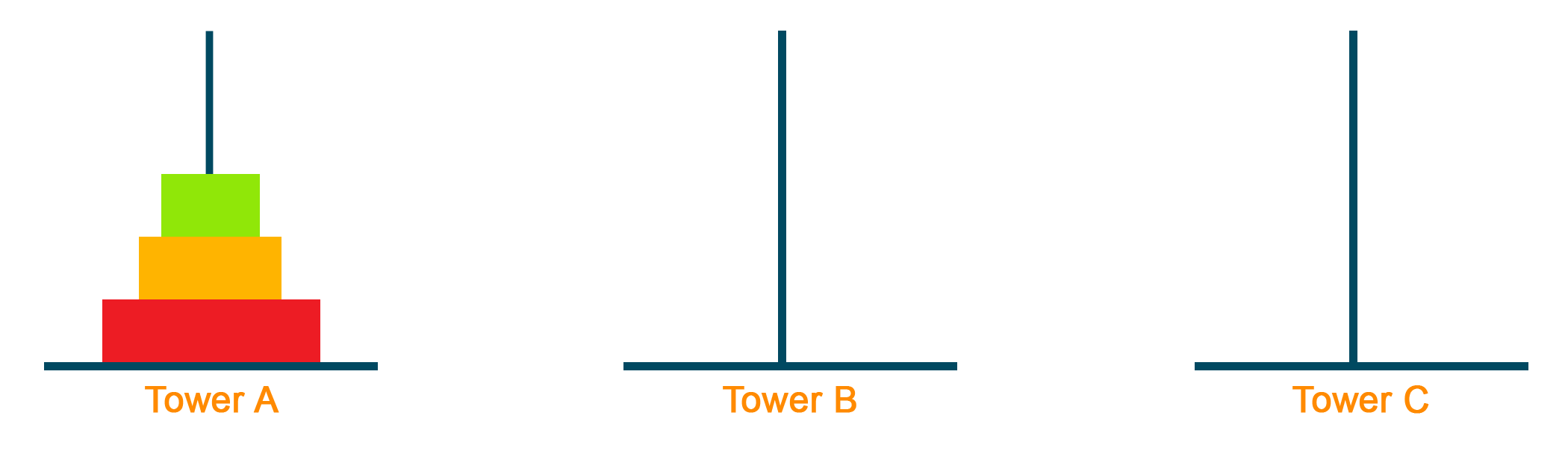
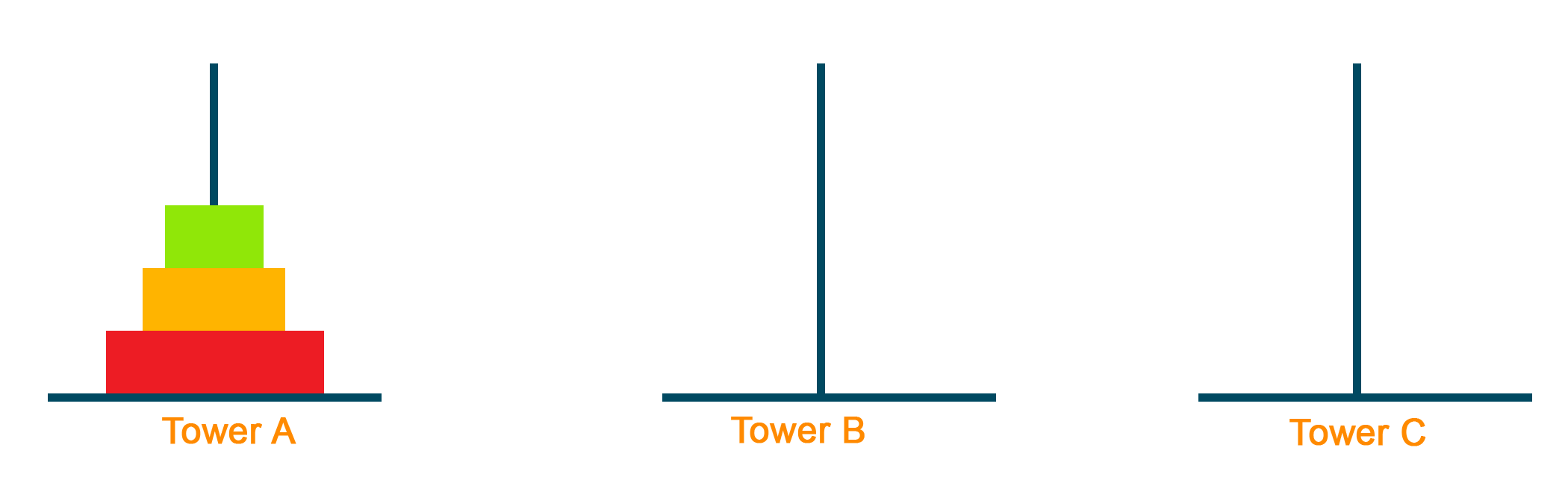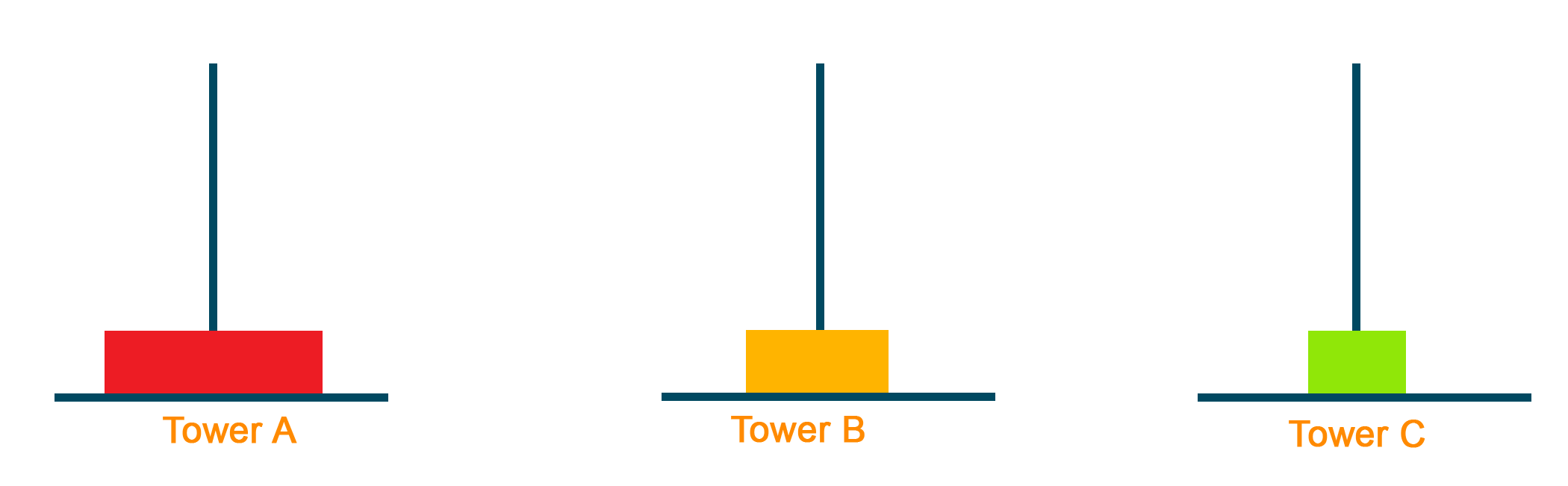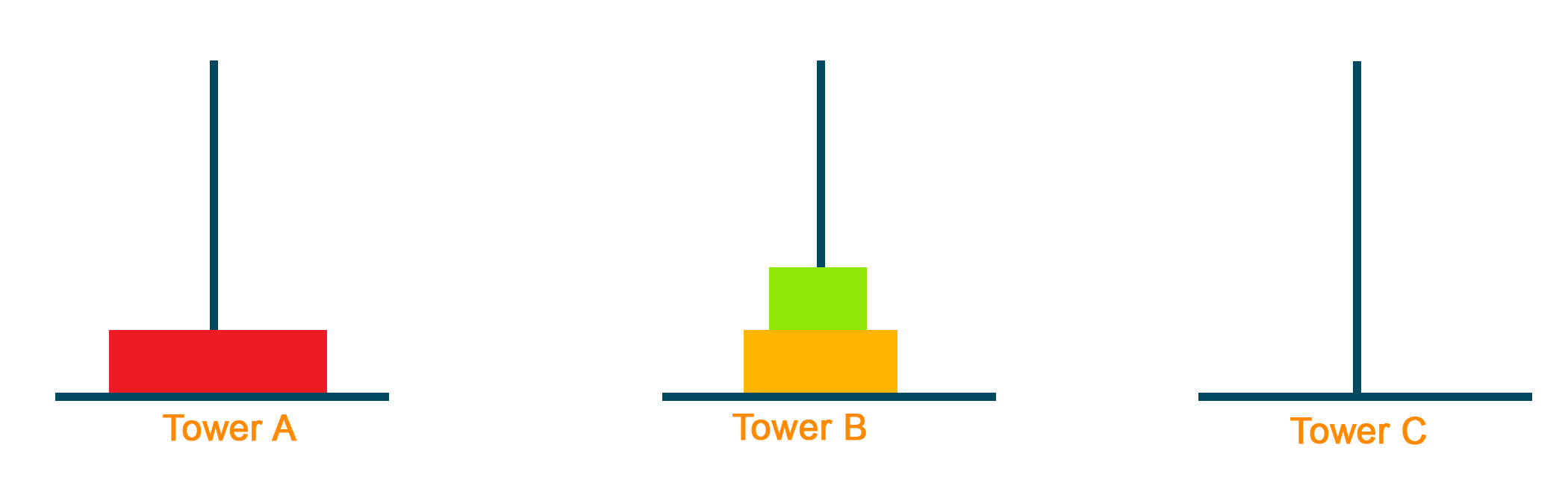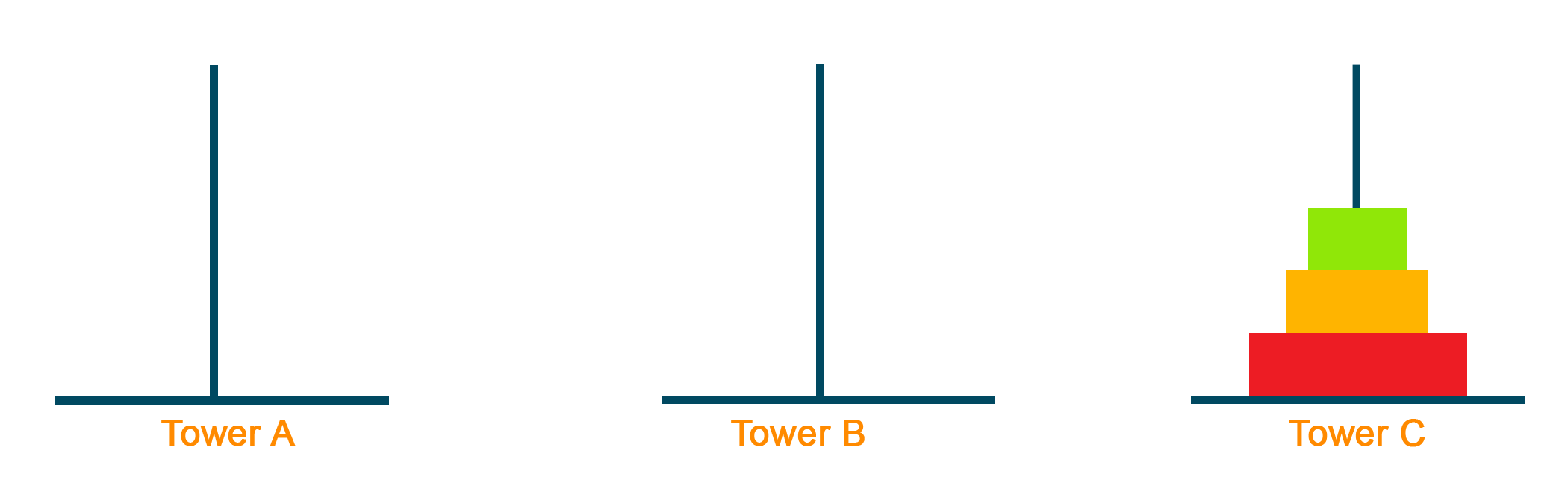
Example 1 - Tower of Hanoi problem
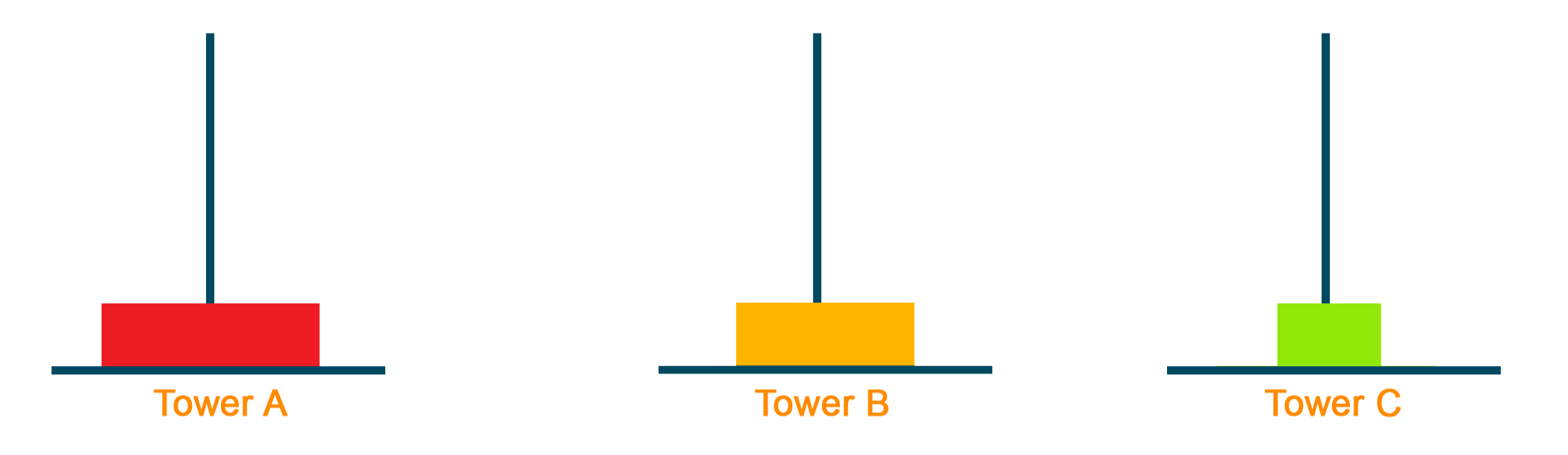
Problem Statement: In the Tower of Hanoi problem, you are given N blocks in decreasing order of size on Tower A and you want to move all these blocks to Tower C with the help of Tower B. Remember that you can move only one block at a time and block can never be on top of a smaller block.
Suppose we take some blocks let, N = 3, the process of moving the blocks from Tower A to Tower C would be as given below:
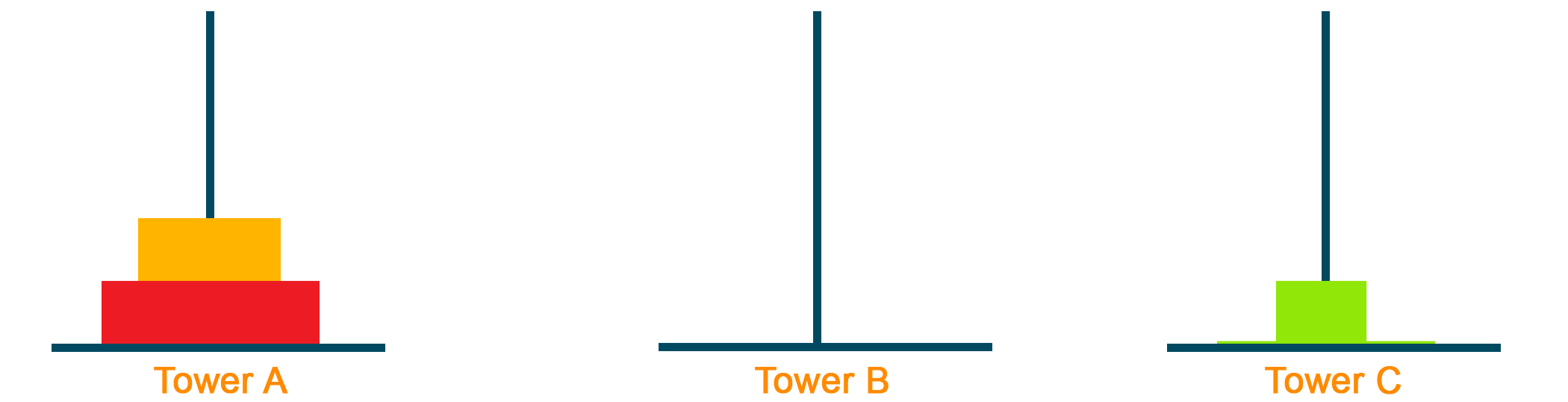
First, move the smallest block to Tower C. This step shows the division of the problem by dividing the number of blocks from N=3 to N=2. Therefore, now we can assume our sub-problem to be moving 2 blocks from Tower A to Tower C.
Then move the middle block to Tower B as given in the figure below. Similar to the above step, we further divided the sub-problem from N=2 to N=1 at the source point.
In this step, we start solving the sub-problems by replacing the smallest block over the middle block in Tower B as given below:

Later, move the biggest block to Tower C from Tower A and move the smallest block to empty Tower A from Tower B.

Lastly, we combine the solution and get the final result by moving the middle block over the biggest block from Tower B to Tower C and moving the smallest block from Tower A to Tower C as shown in the figure below:
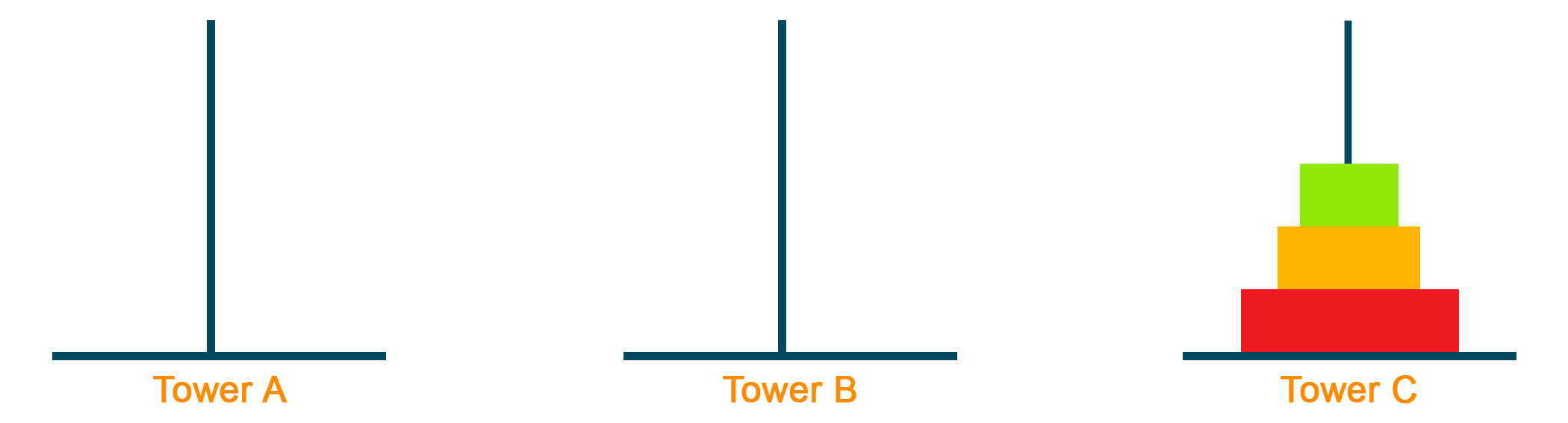
Here's the illustration of the solution for Tower of Hanoi
Python Code For A Tower Of Hanoi
def towerOfHanoi(N , source, destination, auxiliary): if N==1: print("Move disk 1 from source",source,"to destination",destination) return towerOfHanoi(N-1, source, auxiliary, destination) print("Move disk",N,"from source",source,"to destination",destination) towerOfHanoi(N-1, auxiliary, destination, source) # Driver code N = 3 towerOfHanoi(N,'A','B','C') # A, C, B are the name of rods
Output
Move disk 1 from source A to destination B
Move disk 2 from source A to destination C
Move disk 1 from source B to destination C
Move disk 3 from source A to destination B
Move disk 1 from source C to destination A
Move disk 2 from source C to destination B
Move disk 1 from source A to destination B
Example 2: Find the minimum and maximum elements in an array.
Problem Statement: In this problem, we are given an array of elements and we have to find the minimum and maximum element from the given array. We will solve the given problem by the divide and conquer algorithm. Here, we divide the elements as the first step of the divide and conquer algorithm, find the minimum and maximum elements from the array as conquering the solution and finalize the answer at the end by combining the results.
Python Code For Finding Minimum And Maximum Element In Array
def divideAndConquer_Max(arr, ind, len): maximum = -1; if (ind >= len - 2): if (arr[ind] > arr[ind + 1]): return arr[ind]; else: return arr[ind + 1]; maximum = divideAndConquer_Max(arr, ind + 1, len); if (arr[ind] > maximum): return arr[ind]; else: return maximum; def divideAndConquer_Min(arr, ind, len): minimum = 0; if (ind >= len - 2): if (arr[ind] < arr[ind + 1]): return arr[ind]; else: return arr[ind + 1]; minimum = divideAndConquer_Min(arr, ind + 1, len); if (arr[ind] < minimum): return arr[ind]; else: return minimum; if __name__ == '__main__': minimum, maximum = 0, -1; # array initialization arr = [6, 4, 8, 90, 12, 56, 7, 1, 63]; maximum = divideAndConquer_Max(arr, 0, 9); minimum = divideAndConquer_Min(arr, 0, 9); print("The minimum number in the array is: ", minimum); print("The maximum number in the array is: ", maximum);
Output
The minimum number in the array is: 1
The maximum number in the array is: 90
Divide and Conquer vs Dynamic Programming Algorithm
|
Divide and Conquer
|
Dynamic Programming
|
|
It includes 3 steps to reach the solution: Divide: Dividing the original problem into a smaller sub-problem Conquer: Solving sub-problem recursively Combine: Combine the solution of the sub-problem to find a final solution |
It includes 4 steps to reach the solution: Characterizing the structure of an optimal solution Define the value of an optimal solution recursively Using the bottom-up algorithm, calculate the value of an optimal solution Using computed information, construct an optimal solution |
|
It is recursive in nature |
It is non-recursive in nature |
|
It recursively works on sub-problems and hence consumes more time |
It solves the sub-problem only once, and therefore it consumes less time |
|
It is a top-down algorithm |
It is a bottom-up algorithm |
|
Sub-problems are independent in nature |
Sub-problems are interdependent in nature |
|
Example: Linear search and Merge sort |
Example: Matrix Multiplication
|
Advantages of Divide and Conquer Algorithm
- The divide and conquer algorithm is easy and effective to solve difficult problems by breaking them into sub-problems
- The divide and conquer algorithm helps to solve the sub-problem independently
- The divide and conquer algorithm makes effective and efficient use of memory caches
- The divide and conquer algorithm is often used in sorting algorithms like merge sort, quick sort, etc
- It is also used in searching algorithms like a linear search and binary search
- The round of control in such an algorithm is very efficient and therefore, it is better to use the divide and conquer algorithm while dealing with floating numbers.
- Divide and conquer algorithms does not require any modifications
Disadvantages of Divide and Conquer Algorithm
- In the divide and conquer algorithm, the recursion of the sub-problem is slow
- For some specific problems, the divide and conquer method becomes complicated in comparison to the iterative method
Applications
- The divide and conquer algorithm is used to find min and max
- The divide and conquer algorithm is used in the binary search algorithm
- It is used to find the power of the element
- Divide and conquer is the major algorithm in merge sort and quick sort
- Merge sort is used in selection procedures
- It is used Strassen's algorithm for matrix multiplication
- It is used in karatsuba Algorithm
- Merge sort is used in the cooley-Tukey Algorithm
Conclusion
As we studied, the divide and conquer algorithm has many benefits that make it a very useful and important problem-solving algorithm. It helps to solve difficult problems in 3 simple steps using the top-down algorithm recursively. This basic idea of the divide and conquer algorithm can be related to everyday life with lots of practical applications and hence it is important to learn and understand the divide and conquer algorithm.