Solving Tower of Hanoi using Stack & Recursion (with C++ code)

The Tower of Hanoi problem is a classic mathematical puzzle that has intrigued mathematicians, and puzzle enthusiasts. In this article, we will delve into the intricacies of the Tower of Hanoi problem, exploring its history, rules, strategies, and applications.

Tower of Hanoi Problem

The Tower of Hanoi puzzle consists of three pegs (often represented by rods) and a set of disks of different sizes. The disks can be stacked onto the pegs, with the largest disk at the bottom and the smallest disk at the top. The objective is to move the entire stack from one peg, known as the source peg, to another peg, known as the target peg, using the third peg, called the auxiliary peg, as temporary storage.

The puzzle follows three simple rules:

• Only one disk can be moved at a time: You can only move the topmost disk from any stack of disks on a peg.
• Larger disks cannot be placed on top of smaller disks: At no point during the puzzle can you place a larger disk on top of a smaller one
• Use the auxiliary peg for temporary storage: You can utilize the auxiliary peg to temporarily store disks while moving them from the source peg to the target peg.

Let's consider an illustrative example of the Tower of Hanoi problem with 3 disks.

We have three pegs: A, B, and C. The initial configuration of the disks is as follows:

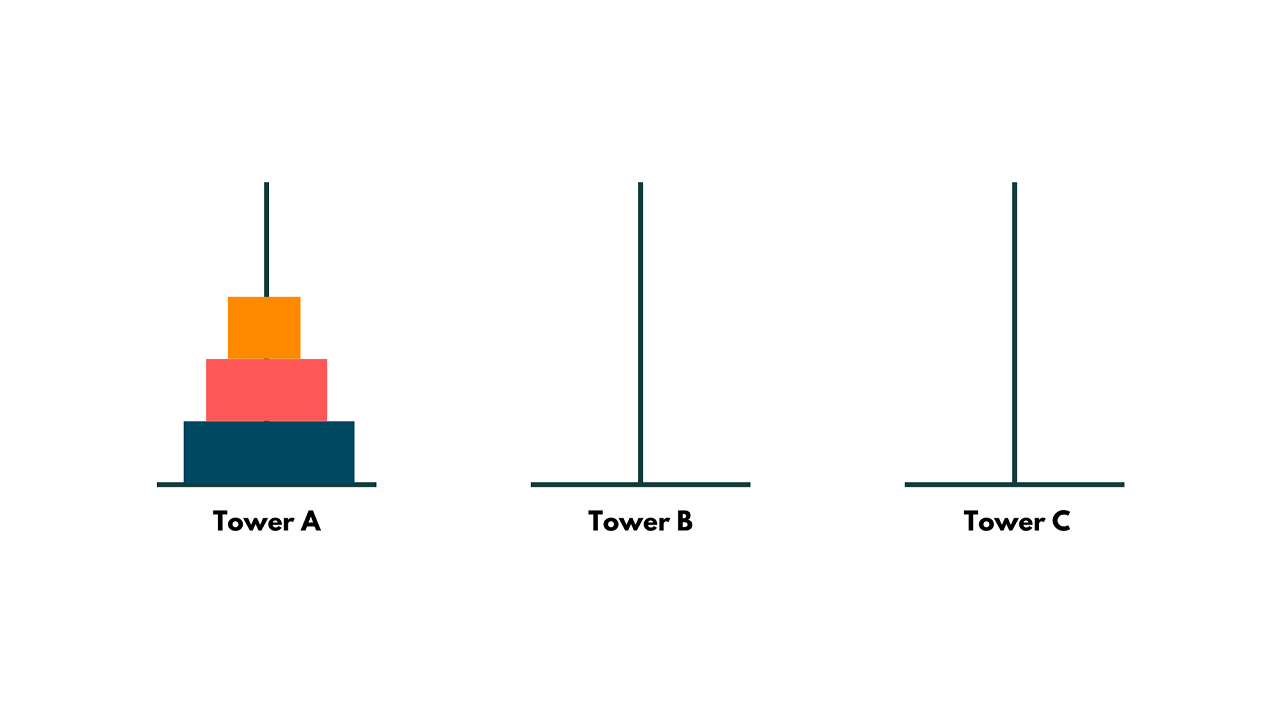
The smallest block should be moved to Tower C first. In this stage, the number of blocks is reduced from N = 3 to N = 2, illustrating how the issue has been divided. We may now imagine that our secondary issue is traveling from Tower A to Tower C over a distance of two blocks. 

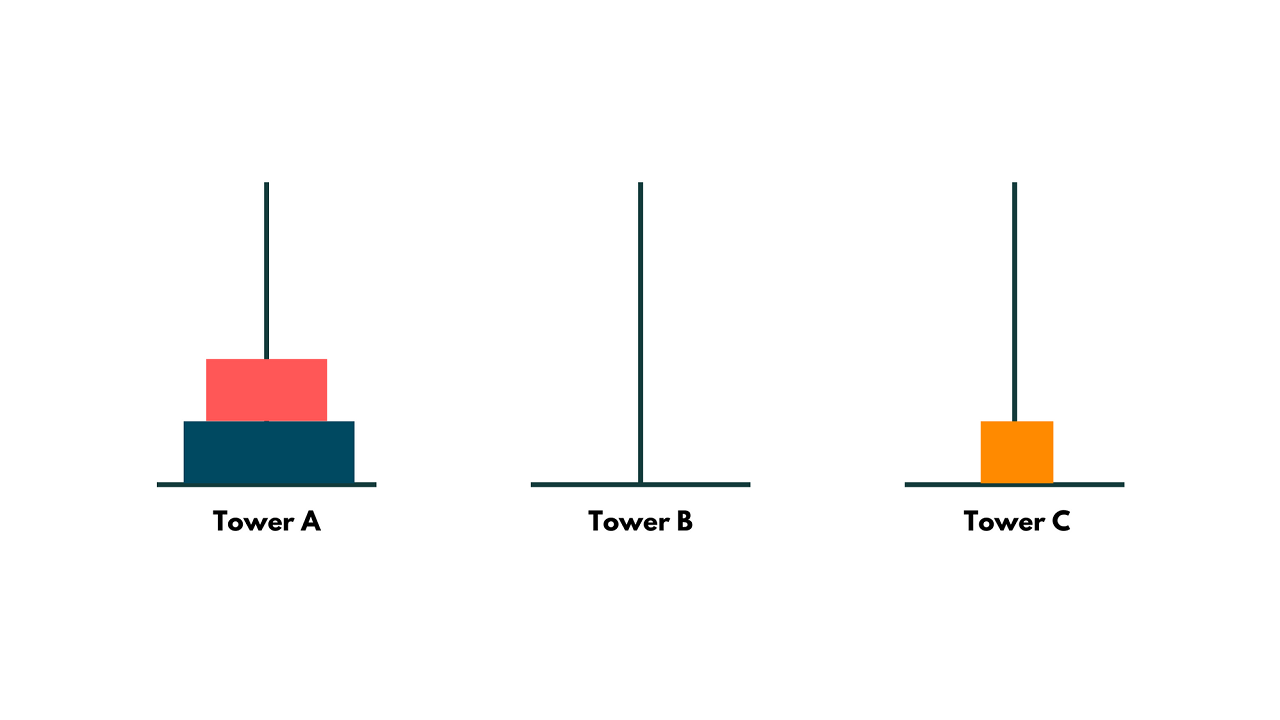
Then, as seen in the diagram below, transfer the center block to Tower B. At the source point, we further separated the sub-problem from N=2 to N=1 in a manner similar to the previous phase.

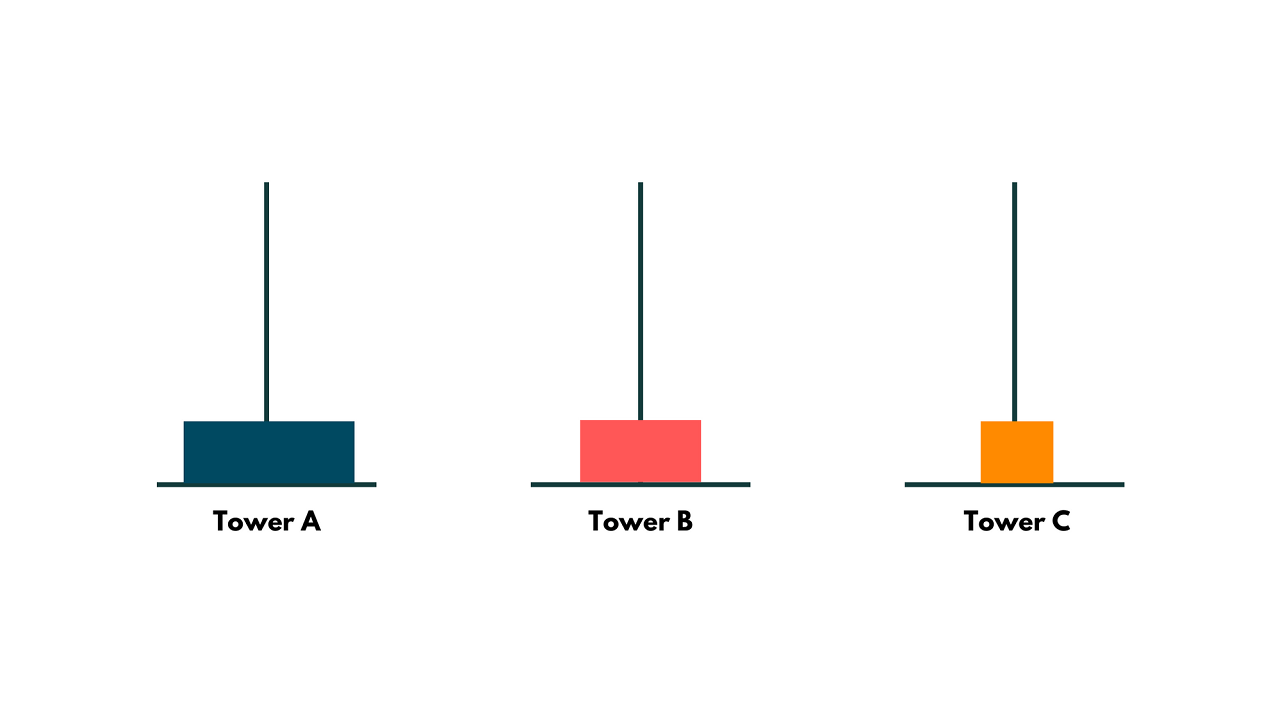
By moving the smallest block in Tower B over the middle block, we may begin to solve the subproblems in this phase, as shown below:

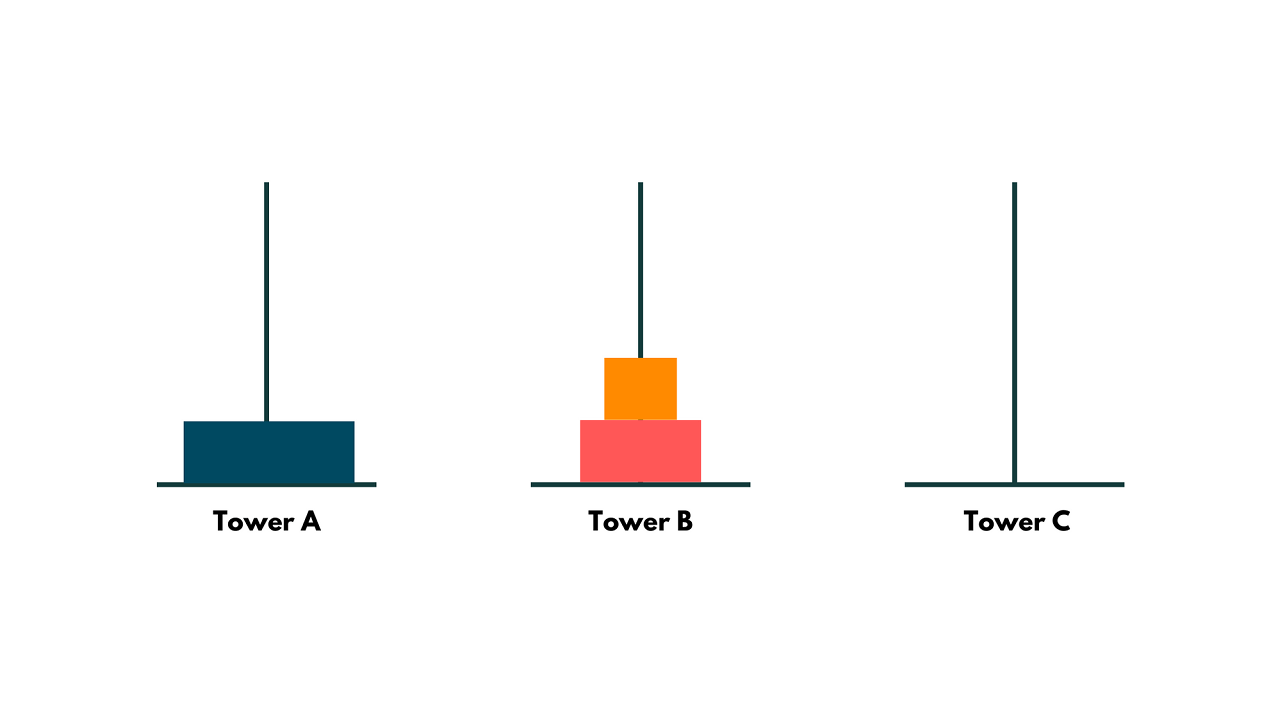
Later, transfer the largest block from Tower A to Tower C and the smallest block from Tower B to the vacant Tower A.

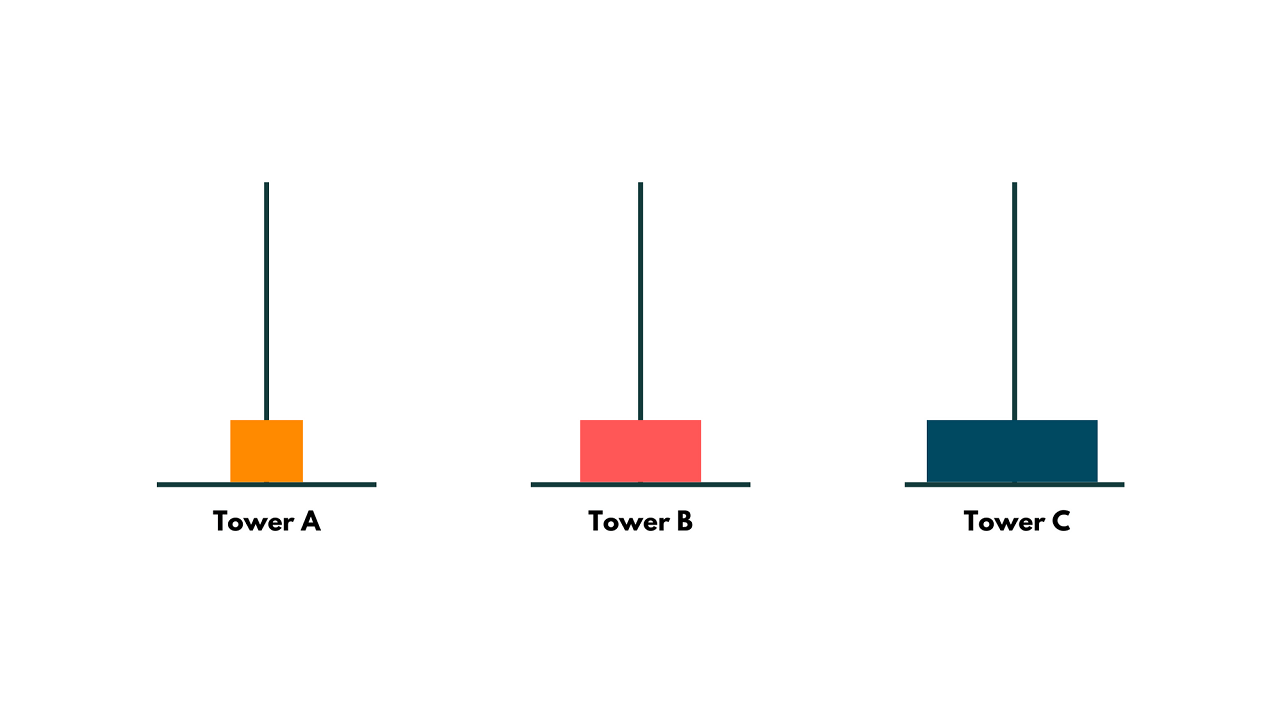
Then, as illustrated in the following diagram, we combine the solution to arrive at the ultimate outcome by moving the middle block over the largest block from Tower B to Tower C and transferring the smallest block from Tower A to Tower C.

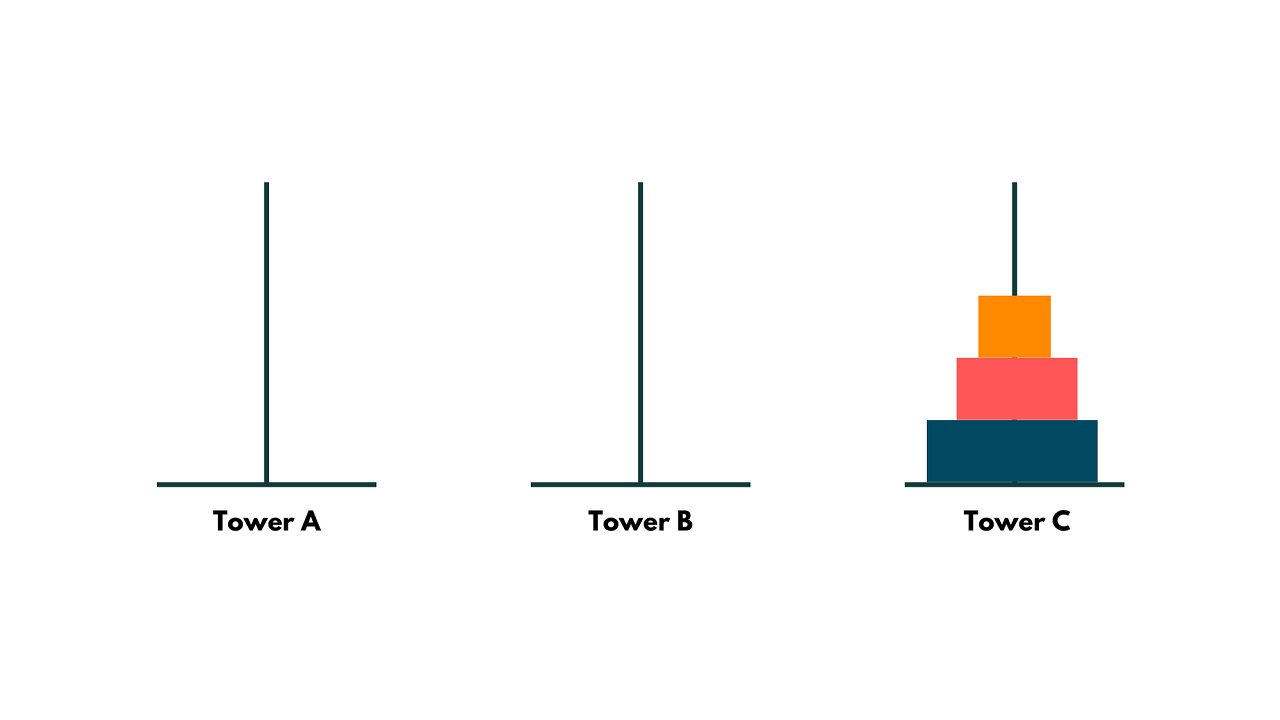
Now you understood the problem, let's move forward to solve it.

Tower Of Hanoi Using Recursion

To solve the Tower of Hanoi problem using recursion, we can break it down into smaller subproblems. Here is the recursive algorithm for solving the Tower of Hanoi problem:

void TowerOfHanoi(int n, char source, char target, char auxiliary) {
    if (n > 0) {
        // Move n-1 disks from source to auxiliary using target as the temporary peg
        TowerOfHanoi(n - 1, source, auxiliary, target);
        
        // Move the nth disk from source to target
        std::cout << "Move disk " << n << " from " << source << " to " << target << std::endl;
        
        // Move n-1 disks from auxiliary to target using source as the temporary peg
        TowerOfHanoi(n - 1, auxiliary, target, source);
    }
}

In the above algorithm, the TowerOfHanoi function takes four parameters: n (the number of disks), source (the peg from which to move the disks), target (the peg to which the disks should be moved), and auxiliary (the temporary peg used for storage during the moves).

The base case of the recursion occurs when n is 0, in which case no moves need to be made. Otherwise, the recursive steps involve:

1. Moving n-1 disks from the source peg to the auxiliary peg using the target peg as temporary storage.
2. Moving the nth disk from the source peg to the target peg.
3. Moving the n-1disks from the auxiliary peg to the target peg using the source peg as temporary storage.

Let's implement the Tower of Hanoi problem in C++ using the recursive algorithm mentioned above:

#include <iostream>

void TowerOfHanoi(int n, char source, char target, char auxiliary) {
    if (n > 0) {
        TowerOfHanoi(n - 1, source, auxiliary, target);
        std::cout << "Move disk " << n << " from " << source << " to " << target << std::endl;
        TowerOfHanoi(n - 1, auxiliary, target, source);
    }
}

int main() {
    int numDisks;
    std::cout << "Enter the number of disks: ";
    std::cin >> numDisks;

    TowerOfHanoi(numDisks, 'A', 'C', 'B');

    return 0;
}

Output:

Enter the number of disks: 3
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C

In this implementation, the main function prompts the user to enter the number of disks they want to solve the Tower of Hanoi problem for. It then calls the TowerOfHanoi function with the appropriate arguments.

The time complexity of solving the Tower of Hanoi problem is exponential, O(2^n), where n is the number of disks. The space complexity is linear, O(n), where n is the number of disks.

Tower of Hanoi using Stack

To solve the Tower of Hanoi problem using stacks, we can simulate the movement of disks between pegs by keeping track of the current state using three stacks: source, target, and auxiliary.

Here is an implementation of the Tower of Hanoi problem in C++ using stacks:

#include <iostream>
#include <stack>
#include <bits/stdc++.h>

void TowerOfHanoi(int numDisks, std::stack<int>& source, std::stack<int>& target, std::stack<int>& auxiliary) {
    int totalMoves = pow(2, numDisks) - 1;
    
    for (int move = 1; move <= totalMoves; move++) {
        if (move % 3 == 1) {
            if (!source.empty() && (auxiliary.empty() || source.top() < auxiliary.top())) {
                auxiliary.push(source.top());
                source.pop();
                std::cout << "Move disk from source to auxiliary" << std::endl;
            }
            else {
                source.push(auxiliary.top());
                auxiliary.pop();
                std::cout << "Move disk from auxiliary to source" << std::endl;
            }
        }
        else if (move % 3 == 2) {
            if (!source.empty() && (target.empty() || source.top() < target.top())) {
                target.push(source.top());
                source.pop();
                std::cout << "Move disk from source to target" << std::endl;
            }
            else {
                source.push(target.top());
                target.pop();
                std::cout << "Move disk from target to source" << std::endl;
            }
        }
        else {
            if (!auxiliary.empty() && (target.empty() || auxiliary.top() < target.top())) {
                target.push(auxiliary.top());
                auxiliary.pop();
                std::cout << "Move disk from auxiliary to target" << std::endl;
            }
            else {
                auxiliary.push(target.top());
                target.pop();
                std::cout << "Move disk from target to auxiliary" << std::endl;
            }
        }
    }
}

int main() {
    int numDisks;
    std::cout << "Enter the number of disks: ";
    std::cin >> numDisks;
    
    std::stack<int> source, target, auxiliary;
    
    // Initialize the source stack with disks
    for (int i = numDisks; i >= 1; i--) {
        source.push(i);
    }
    
    TowerOfHanoi(numDisks, source, target, auxiliary);
    
    return 0;
}

Output:

Enter the number of disks: 3
Move disk from source to auxiliary
Move disk from source to target
Move disk from auxiliary to target
Move disk from source to auxiliary
Move disk from target to source
Move disk from target to auxiliary
Move disk from source to auxiliary

In this implementation, we define a TowerOfHanoi function that takes the number of disks, along with three stacks: source, target, and auxiliary. We calculate the total number of moves required based on the number of disks.

Within the main loop, we use the modulo operator to determine the type of move to be made based on the current iteration. The logic ensures that the disks are moved according to the Tower of Hanoi rules, taking into account the current state of the stacks.

The time complexity of the Tower of Hanoi solution using stacks is O(2^n), where n is the number of disks. This is because the number of moves required to solve the Tower of Hanoi problem grows exponentially with the number of disks. For each disk, there are two possible moves, leading to a total of 2^n moves.

The space complexity of the Tower of Hanoi solution using stacks is O(n), where n is the number of disks. This is because the space required by the algorithm is directly proportional to the number of disks. In the worst case, each stack can hold all the disks, resulting in a space requirement of O(n) for the stacks. 

Conclusion

We have studied two ways to solve the Tower of Hanoi problem using Stack and Recursion in C++. It is a problem that requires logical thinking, strategic planning, and a deep understanding of recursive algorithms.