Searching Algorithms - Linear and Binary Search (Python)

In this article, we will study what searching algorithms are and the types of searching algorithms i.e linear search and binary search in detail. We will learn their algorithm along with the python code and examples of the searching algorithms in detail. Lastly, we will understand the time complexity and application of the searching algorithm. So, let's get started!

What is a searching algorithm?

There is not even a single day when we don’t want to find something in our daily life. The same thing happens with the computer system. When the data is stored in it and after a certain amount of time the same data is to be retrieved by the user, the computer uses the searching algorithm to find the data. The system jumps into its memory, processes the search of data using the searching algorithm technique, and returns the data that the user requires. Therefore, the searching algorithm is the set of procedures used to locate the specific data from the collection of data. The searching algorithm is always considered to be the fundamental procedure of computing. And hence it is always said that the difference between the fast application and slower application is often decided by the searching algorithm used by the application.

There are many types of searching algorithms possible like linear search, binary search, jump search, exponential search, Fibonacci search, etc. In this article, we will learn linear search and binary search in detail with algorithms, examples, and python code.

What is Linear Search?

Linear search is also known as a sequential searching algorithm to find the element within the collection of data. The algorithm begins from the first element of the list, starts checking every element until the expected element is found. If the element is not found in the list, the algorithm traverses the whole list and return “element not found”. Therefore, it is just a simple searching algorithm.

Example:

Consider the below array of elements. Now we have to find element a = 1 in the array given below.

We will start with the first element of the array, compare the first element with the element to be found. If the match is not found, we will jump to the next element of the array and compare it with the element to be searched i.e ‘a’.

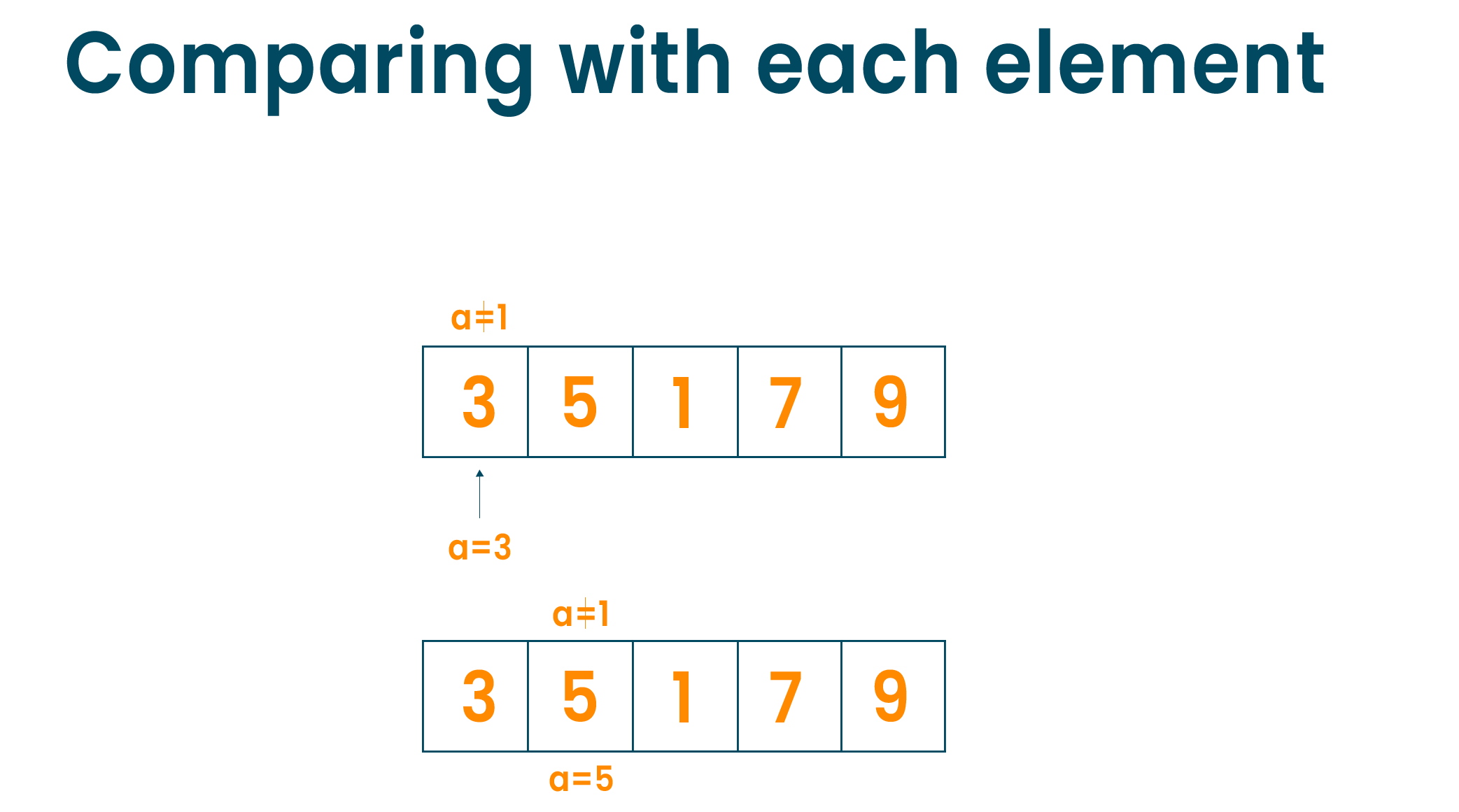
If the element is found, we will return the index of that element else, we will return 'element not found'.

Linear Search Algorithm

LinearSearch(array, key)
    for each element in the array
        if element == value
            return its index

Python Program for Linear Search

def LinearSearch(array, n, k):

    for j in range(0, n):

        if (array[j] == k):

            return j

    return -1

 
array = [1, 3, 5, 7, 9]

k = 7
n = len(array)

result = LinearSearch(array, n, k)

if(result == -1):

    print("Element not found")

else:

    print("Element found at index: ", result)

Output

Element found at index:  3 

Time Complexity of Linear Search

The running time complexity of the linear search algorithm is O(n) for N number of elements in the list as the algorithm has to travel through each and every element to find the desired element.

Applications of Linear Search

•  Used to find the desired element from the collection of data when the dataset is small
• The searching operations is less than 100 items

What is Binary Search?

Binary search is used with a similar concept, i.e to find the element from the list of elements. Binary search algorithms are fast and effective in comparison to linear search algorithms. The most important thing to note about binary search is that it works only on sorted lists of elements. If the list is not sorted, then the algorithm first sorts the elements using the sorting algorithm and then runs the binary search function to find the desired output. There are two methods by which we can run the binary search algorithm i.e, iterative method or recursive method. The steps of the process are general for both the methods, the difference is only found in the function calling.

Algorithm for Binary Search (Iterative Method)

do until the pointers low and high are equal.

    mid = (low + high)/2

    if (k == arr[mid])

        return mid

    else if (k > arr[mid])           // k is on right side of mid

        low = mid + 1

    else                            // k is on left side of mid

        high = mid - 1

 

Algorithm for Binary Search (Recursive Method)

BinarySearch(array, k, low, high)

    if low > high
        return False 

    else
        mid = (low + high) / 2 

        if k == array[mid]
            return mid

        else if k > array[mid]        // k is on the right side
            return BinarySearch(array, k, mid + 1, high)

        else                               // k is on the right side
            return BinarySearch(array, k, low, mid - 1)

Example

Consider the following array on which the search is performed. Let the element to be found is k=0

Now, we will set two pointers pointing the low to the lowest position in the array and high to the highest position in the array.

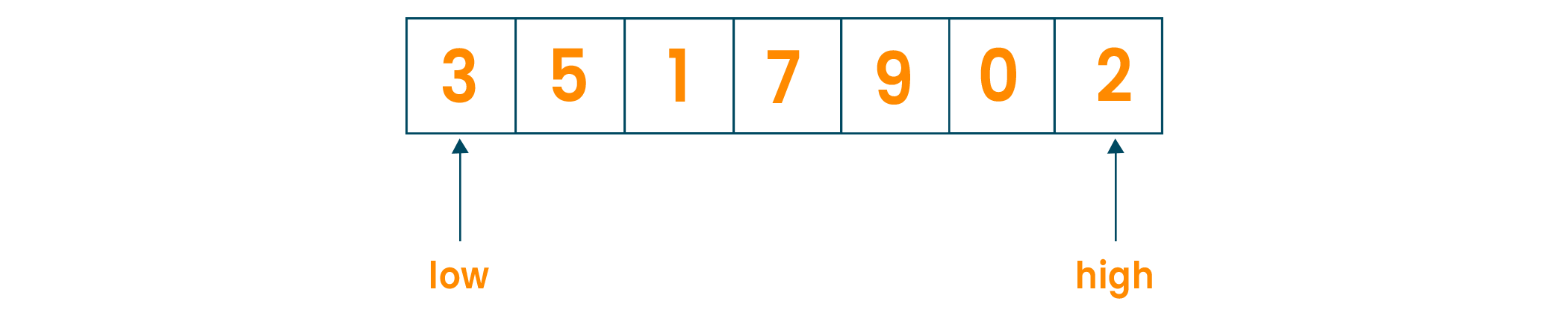
Now, we will find the middle element of the array using the algorithm and set the mid pointer to it.

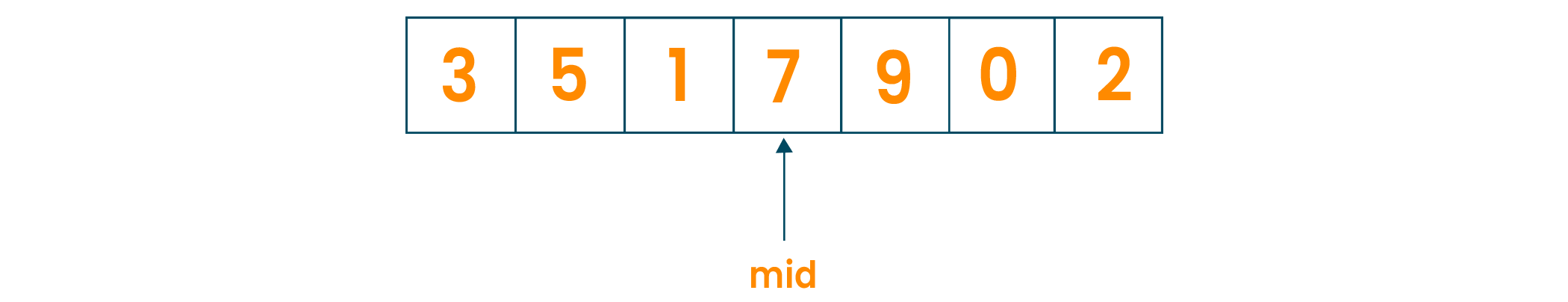
We will compare the mid element with the element to be searched and if it matches, we will return the mid element.

If the element to be searched is greater than the mid, we will set the low pointer to the "mid+1" element and run the algorithm again.

If the element to be searched is lower than the mid element, we will set the high pointer to the "mid-1" element and run the algorithm again.

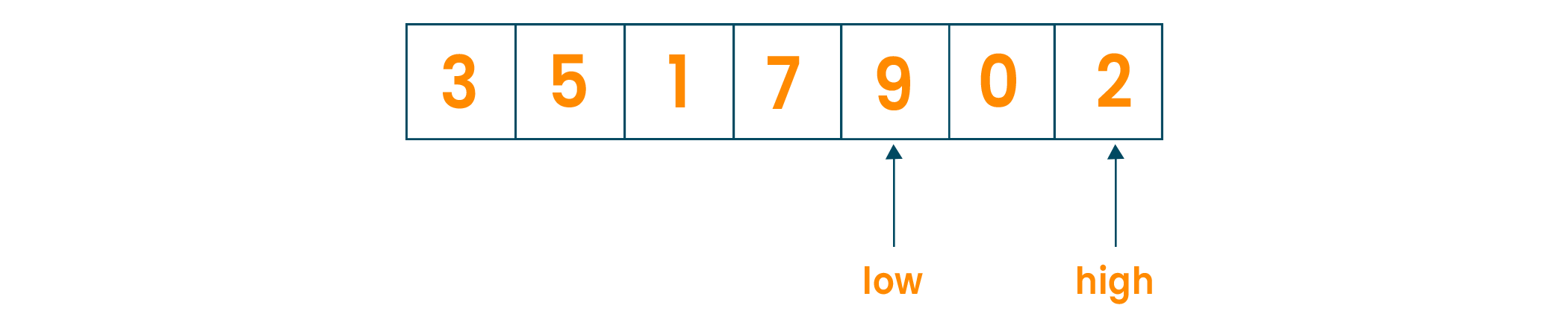
We will repeat the same steps until the low pointer meets the high pointer and we find the desired element.

Python Code for Binary Search (Iterative Method)

def binarySearch(arr, k, low, high):
   
    while low <= high:
        mid = low + (high - low)//2
        if arr[mid] == k:
            return mid
        elif arr[mid] < k:

            low = mid + 1
        else:

            high = mid - 1
    return -1

arr = [1, 3, 5, 7, 9]

k = 5
result = binarySearch(arr, k, 0, len(arr)-1)

if result != -1:

    print("Element is present at index " + str(result))

else:

    print("Not found")

Output

Element is present at index 2 

Python Code for Binary Search (Recursive Method)

def BinarySearch(arr, k, low, high):

    if high >= low:

        mid = low + (high - low)//2

        if arr[mid] == k:
            return mid

        elif arr[mid] > k:
            return BinarySearch(arr, k, low, mid-1)

        else:
            return BinarySearch(arr, k, mid + 1, high)

    else:
        return -1


arr = [1, 3, 5, 7, 9]
k = 5

result = BinarySearch(arr, k, 0, len(arr)-1)

if result != -1:
    print("Element is present at index " + str(result))
else:
    print("Not found")

Output

Element is present at index 2

Time complexity of Binary Search

The running time complexity for binary search is different for each scenario. The best-case time complexity is O(1) which means the element is located at the mid-pointer. The Average and Worst-Case time complexity is O(log n) which means the element to be found is located either on the left side or on the right side of the mid pointer. Here, n indicates the number of elements in the list.

The space complexity of the binary search algorithm is O(1).

Applications of Binary Search

• The binary search algorithm is used in the libraries of Java, C++, etc
• It is used in another additional program like finding the smallest element or largest element in the array
• It is used to implement a dictionary

Difference Between Linear Search and Binary Search

Conclusion

As studied, linear and binary search algorithms have their own importance depending on the application. We often need to find the particular item of data amongst hundreds, thousands, and millions of data collection, and the linear and binary search will help with the same.