While getting into the world of programming, a good many problems will include working with multiple instances of similar types of data. Generally, these data will take the help of arrays for their storage. The bigger question is how to optimize the solution for a particular problem to fit within a particular amount of time? The generalized answer is arranging the elements within the array in such a way that an order is maintained. This is the process of sorting, used in many programming languages like Java. Here are the 5 most popular and most used sorting algorithms in java, along with time complexity. These are the best sorting methods in java currently in the industry.
What is a Sorting Algorithm?
Sorting is a class of algorithms that are tasked with rearranging the positions of elements of an array such that all of its elements are either in ascending or descending order. A good sorting algorithm also needs to ensure that elements having the same value don’t change their locations in the sorted array. Sorting is necessary for getting a concrete understanding of data structures and algorithms.
5 Popular Sorting Algorithms in Java
Java is a flexible language in itself and supports the operation of a variety of sorting algorithms. Most of these algorithms are extremely flexible themselves and can be implemented with both a recursive as well as an iterative approach. Here are 5 most popular sorting algorithms in java:
- Merge Sort
- Heap Sort
- Insertion Sort
- Selection Sort
- Bubble Sort
Let’s learn about each of these java sorting algorithms in detail.
1) Merge Sort
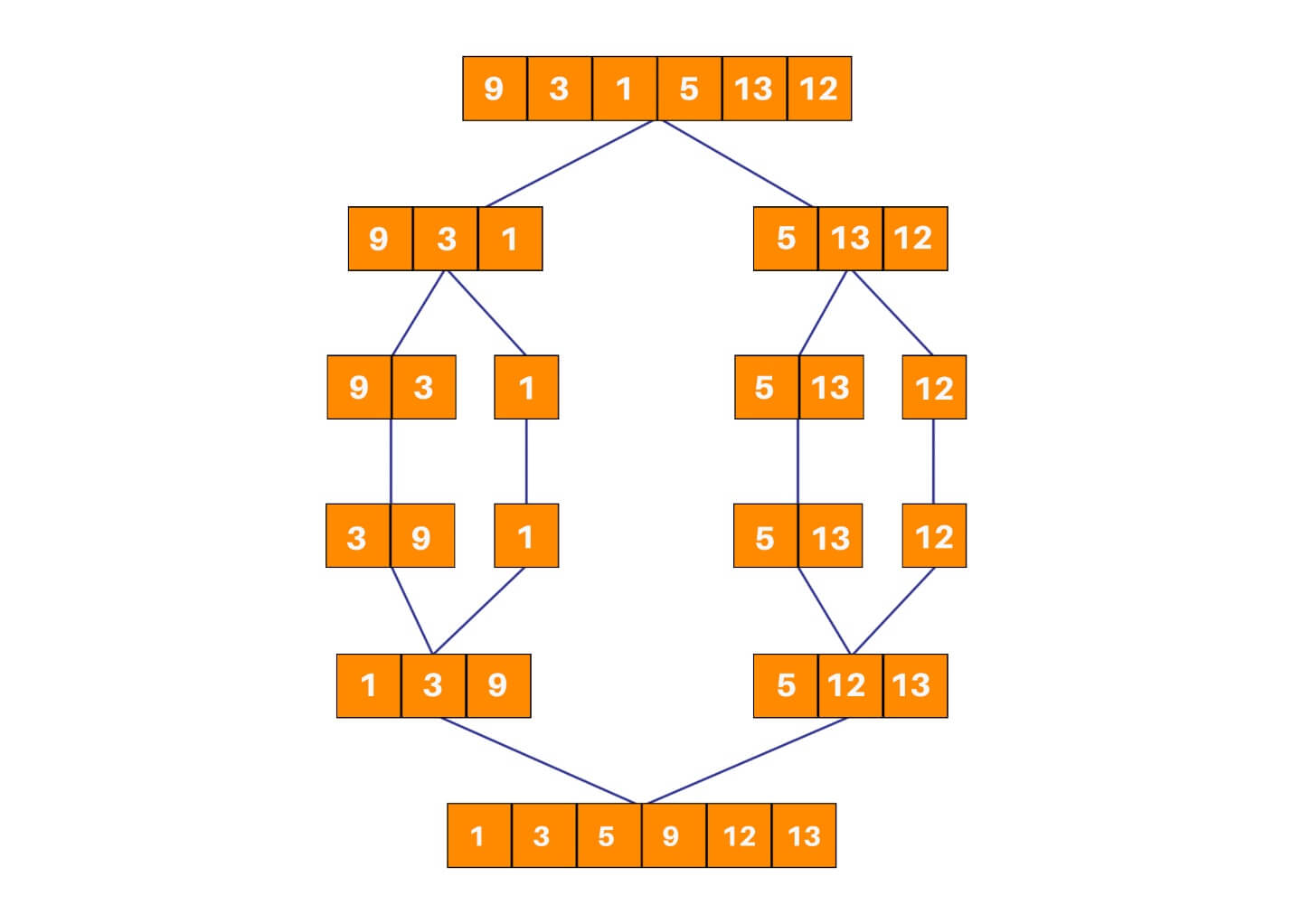
Merge sort in Java is one of the most flexible sorting algorithms in java known to mankind (yes, no kidding). It uses the divide and conquers strategy for sorting elements in an array. It is also a stable sort, meaning that it will not change the order of the original elements in an array concerning each other. The underlying strategy breaks up the array into multiple smaller segments till segments of only two elements (or one element) are obtained. Now, elements in these segments are sorted and the segments are merged to form larger segments. This process continues till the entire array is sorted.
This algorithm has two main parts:
- mergeSort() – This function calculates the middle index for the subarray and then partitions the subarray into two halves. The first half runs from index left to middle, while the second half runs from index middle+1 to right. After the partitioning is done, this function automatically calls the merge() function for sorting the subarray being handled by the mergeSort() call.
- merge() – This function does the actual heavy lifting for the sorting process. It requires the input of four parameters – the array, the starting index (left), the middle index (middle), and the ending index (right). Once received, merge() will split the subarray into two subarrays – one left subarray and one right subarray. The left subarray runs from index left to middle, while the right subarray runs from index middle+1 to right. This function then merges the two subarrays to get the sorted subarray.
Merge Sort Java Code:
class Sort { void merge(int arr[], int left, int middle, int right) { int low = middle - left + 1; //size of the left subarray int high = right - middle; //size of the right subarray int L[] = new int[low]; //create the left and right subarray int R[] = new int[high]; int i = 0, j = 0; for (i = 0; i < low; i++) //copy elements into left subarray { L[i] = arr[left + i]; } for (j = 0; j < high; j++) //copy elements into right subarray { R[j] = arr[middle + 1 + j]; } int k = left; //get starting index for sort i = 0; //reset loop variables before performing merge j = 0; while (i < low && j < high) //merge the left and right subarrays { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } while (i < low) //merge the remaining elements from the left subarray { arr[k] = L[i]; i++; k++; } while (j < high) //merge the remaining elements from right subarray { arr[k] = R[j]; j++; k++; } } void mergeSort(int arr[], int left, int right) //helper function that creates the sub cases for sorting { int middle; if (left < right) { //sort only if the left index is lesser than the right index (meaning that sorting is done) middle = (left + right) / 2; mergeSort(arr, left, middle); //left subarray mergeSort(arr, middle + 1, right); //right subarray merge(arr, left, middle, right); //merge the two subarrays } } void display(int arr[]) //display the array { for (int i=0; i<arr.length; ++i) { System.out.print(arr[i]+" "); } } public static void main(String args[]) { int arr[] = { 9, 3, 1, 5, 13, 12 }; Sort ob = new Sort(); ob.mergeSort(arr, 0, arr.length - 1); ob.display(arr); } }
Explanation of how it works
2) Heap Sort
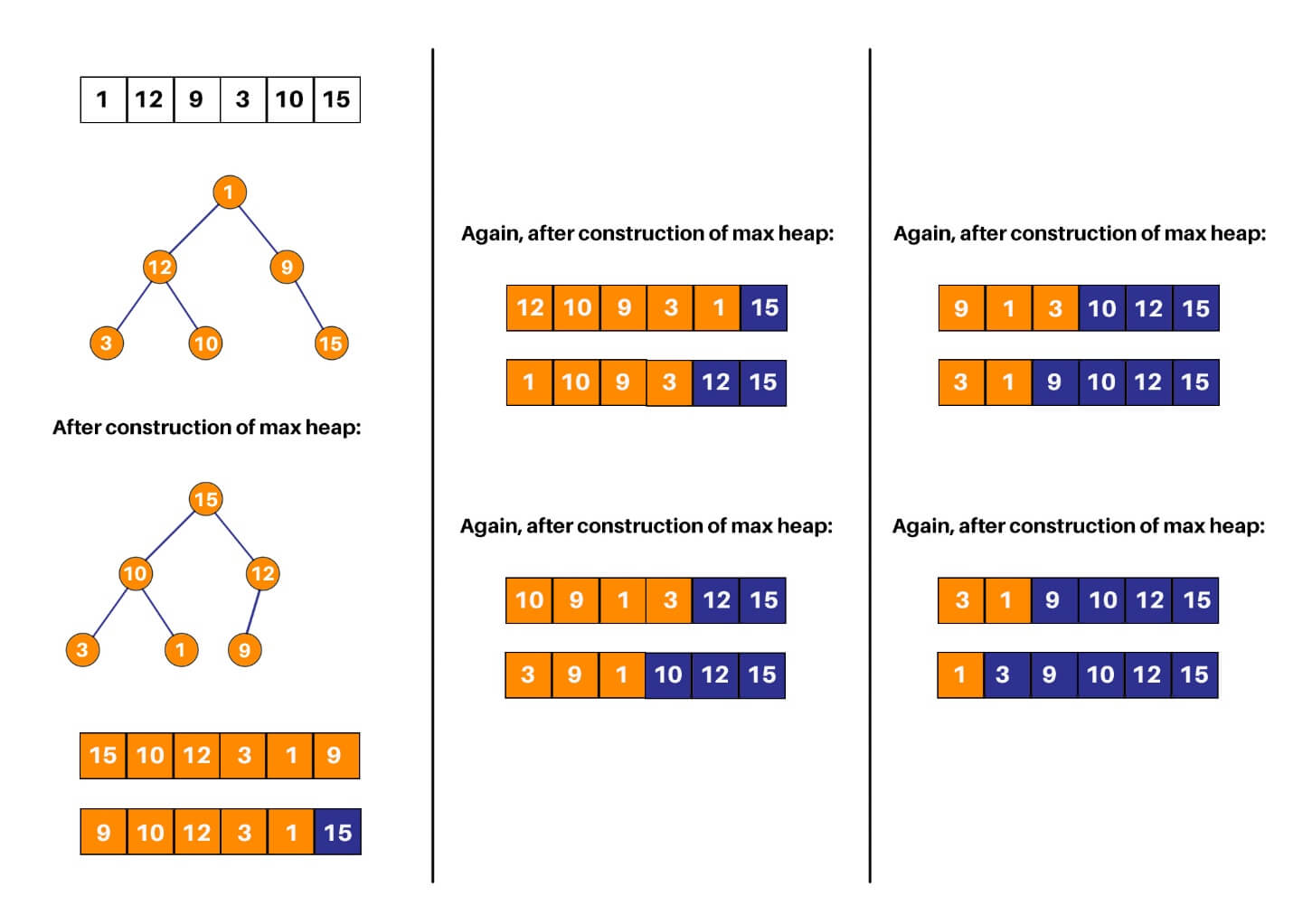
Heap sort is one of the most important sorting methods in java that one needs to learn to get into sorting. It combines the concepts of a tree as well as sorting, properly reinforcing the use of concepts from both. A heap is a complete binary search tree where items are stored in a special order depending on the requirement. A min-heap contains the minimum element at the root, and every child of the root must be greater than the root itself. The children at the level after that must be greater than these children, and so on. Similarly, a max-heap contains the maximum element at the root. For the sorting process, the heap is stored as an array where for every parent node at the index i, the left child is at index 2 * i + 1, and the right child is at index 2 * i + 2.
A max heap is built with the elements of the unsorted array, and then the maximum element is extracted from the root of the array and then exchanged with the last element of the array. Once done, the max heap is rebuilt for getting the next maximum element. This process continues till there is only one node present in the heap.
This algorithm has two main parts:-
- heapSort() – This function helps construct the max heap initially for use. Once done, every root element is extracted and sent to the end of the array. Once done, the max heap is reconstructed from the root. The root is again extracted and sent to the end of the array, and hence the process continues.
- heapify() – This function is the building block of the heap sort algorithm. This function determines the maximum from the element being examined as the root and its two children. If the maximum is among the children of the root, the root and its child are swapped. This process is then repeated for the new root. When the maximum element in the array is found (such that its children are smaller than it) the function stops. For the node at index i, the left child is at index 2 * i + 1, and the right child is at index 2 * i + 1. (indexing in an array starts from 0, so the root is at 0).
Heap Sort Java Code:
class Sort { public void heapSort(int arr[]) { int temp; for (int i = arr.length / 2 - 1; i >= 0; i--) //build the heap { heapify(arr, arr.length, i); } for (int i = arr.length - 1; i > 0; i--) //extract elements from the heap { temp = arr[0]; //move current root to end (since it is the largest) arr[0] = arr[i]; arr[i] = temp; heapify(arr, i, 0); //recall heapify to rebuild heap for the remaining elements } } void heapify(int arr[], int n, int i) { int MAX = i; // Initialize largest as root int left = 2 * i + 1; //index of the left child of ith node = 2*i + 1 int right = 2 * i + 2; //index of the right child of ith node = 2*i + 2 int temp; if (left < n && arr[left] > arr[MAX]) //check if the left child of the root is larger than the root { MAX = left; } if (right < n && arr[right] > arr[MAX]) //check if the right child of the root is larger than the root { MAX = right; } if (MAX != i) { //repeat the procedure for finding the largest element in the heap temp = arr[i]; arr[i] = arr[MAX]; arr[MAX] = temp; heapify(arr, n, MAX); } } void display(int arr[]) //display the array { for (int i=0; i<arr.length; ++i) { System.out.print(arr[i]+" "); } } public static void main(String args[]) { int arr[] = { 1, 12, 9 , 3, 10, 15 }; Sort ob = new Sort(); ob.heapSort(arr); ob.display(arr); } }
Explanation of how it works:
3) Insertion Sort
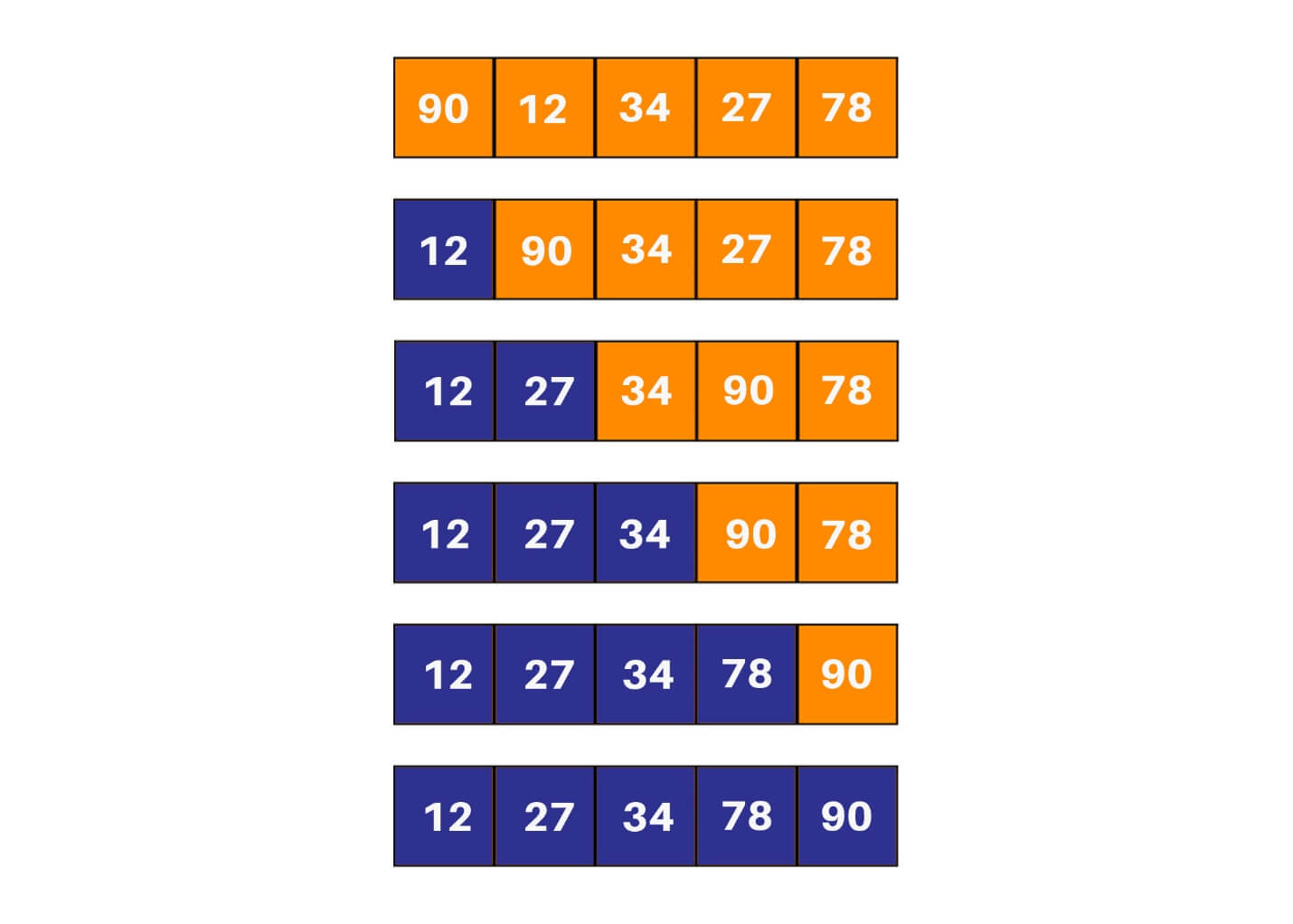
If you’re quite done with more complex sorting algorithms and want to move on to something simpler: insertion sort is the way to go. While it isn’t a much-optimized algorithm for sorting an array, it is one of the more easily understood ones. Implementation is pretty easy too. In insertion sort, one picks up an element and considers it to be the key. If the key is smaller than its predecessor, it is shifted to its correct location in the array.
Algorithm:
- START
- Repeat steps 2 to 4 till the array end is reached.
- Compare the element at current index i with its predecessor. If it is smaller, repeat step 3.
- Keep shifting elements from the “sorted” section of the array till the correct location of the key is found.
- Increment loop variable.
- END
Insertion Sort Java Code:
class Sort { static void insertionSort(int arr[], int n) { if (n <= 1) //passes are done { return; } insertionSort( arr, n-1 ); //one element sorted, sort the remaining array int last = arr[n-1]; //last element of the array int j = n-2; //correct index of last element of the array while (j >= 0 && arr[j] > last) //find the correct index of the last element { arr[j+1] = arr[j]; //shift section of sorted elements upwards by one element if correct index isn't found j--; } arr[j+1] = last; //set the last element at its correct index } void display(int arr[]) //display the array { for (int i=0; i<arr.length; ++i) { System.out.print(arr[i]+" "); } } public static void main(String[] args) { int arr[] = {22, 21, 11, 15, 16}; insertionSort(arr, arr.length); Sort ob = new Sort(); ob.display(arr); } }
Explanation of how it works:
4) Selection Sort
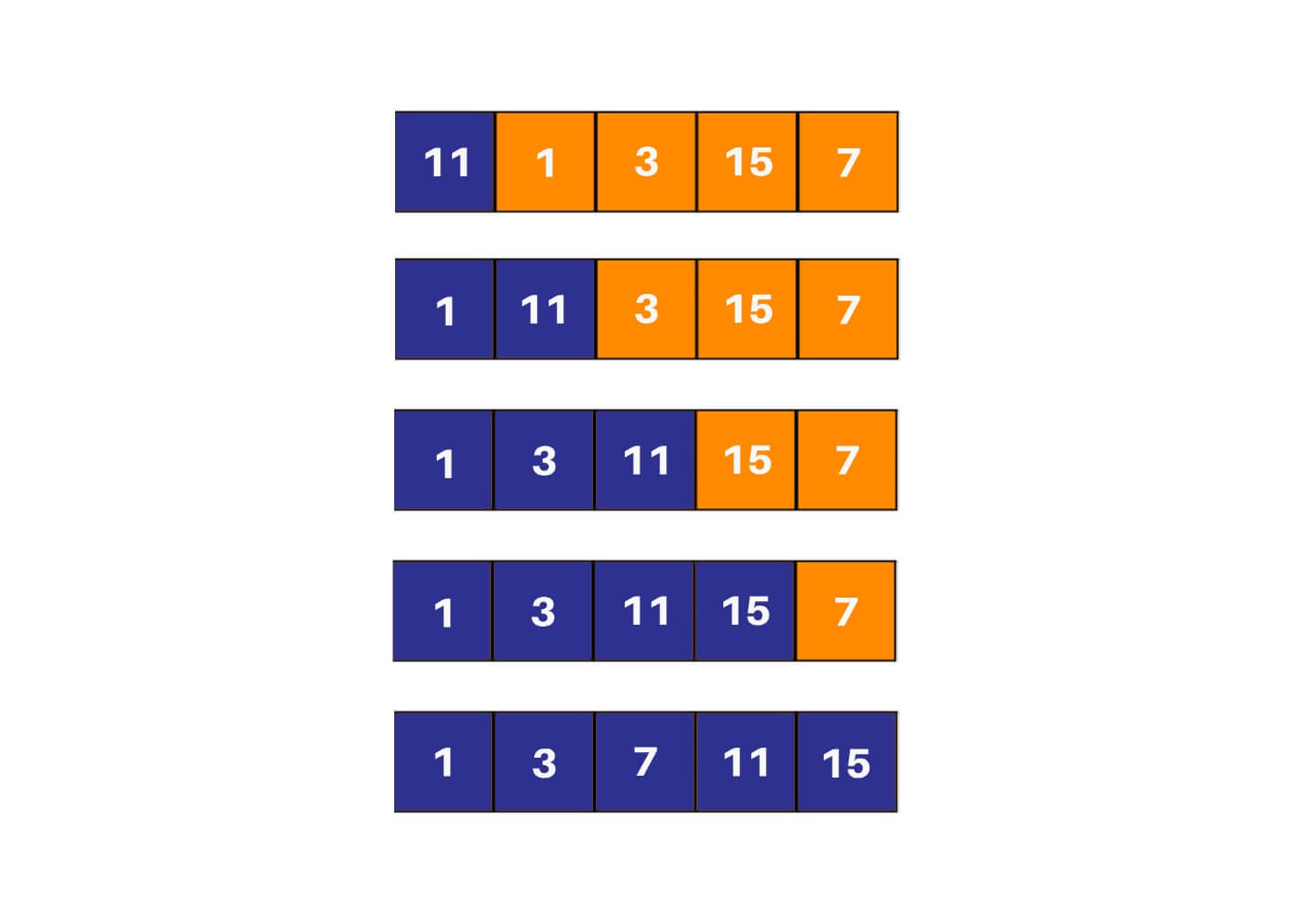
Quadratic sorting algorithms are some of the more popular sorting algorithms that are easy to understand and implement. These don’t offer a unique or optimized approach for sorting the array - rather they should offer building blocks for the concept of sorting itself for someone new to it. In selection sort, two loops are used. The inner loop one picks the minimum element from the array and shifts it to its correct index indicated by the outer loop. In every run of the outer loop, one element is shifted to its correct location in the array. It is a very popular sorting algorithm in python as well.
Algorithm:
- START
- Run two loops: an inner loop and an outer loop.
- Repeat steps till the minimum element are found.
- Mark the element marked by the outer loop variable as a minimum.
- If the current element in the inner loop is smaller than the marked minimum element, change the value of the minimum element to the current element.
- Swap the value of the minimum element with the element marked by the outer loop variable.
- END
Selection Sort Java Code:
class Sort { void selectionSort(int arr[]) { int pos; int temp; for (int i = 0; i < arr.length; i++) { pos = i; for (int j = i+1; j < arr.length; j++) { if (arr[j] < arr[pos]) //find the index of the minimum element { pos = j; } } temp = arr[pos]; //swap the current element with the minimum element arr[pos] = arr[i]; arr[i] = temp; } } void display(int arr[]) //display the array { for (int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } } public static void main(String args[]) { Sort ob = new Sort(); int arr[] = {64,25,12,22,11}; ob.selectionSort(arr); ob.display(arr); } }
Explanation of how it works:
5) Bubble Sort
The two algorithms that most beginners start their sorting career with would be bubble sort and selection sort. These sorting algorithms are not very efficient, but they provide a key insight into what sorting is and how a sorting algorithm works behind the scenes. Bubble sort relies on multiple swaps instead of a single like selection sort. The algorithm continues to go through the array repeatedly, swapping elements that are not in their correct location.
Algorithm:
- START
- Run two loops – an inner loop and an outer loop.
- Repeat steps till the outer loop are exhausted.
- If the current element in the inner loop is smaller than its next element, swap the values of the two elements.
- END
Bubble Sort Java Code:
class Sort { static void bubbleSort(int arr[], int n) { if (n == 1) //passes are done { return; } for (int i=0; i<n-1; i++) //iteration through unsorted elements { if (arr[i] > arr[i+1]) //check if the elements are in order { //if not, swap them int temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; } } bubbleSort(arr, n-1); //one pass done, proceed to the next } void display(int arr[]) //display the array { for (int i=0; i<arr.length; ++i) { System.out.print(arr[i]+" "); } } public static void main(String[] args) { Sort ob = new Sort(); int arr[] = {6, 4, 5, 12, 2, 11, 9}; bubbleSort(arr, arr.length); ob.display(arr); } }
Explanation of how it works:
Btw, here are some good Java project ideas for beginners for you to check and apply these algorithms in practice.
Time Complexity
Now, learn about the time complexity of each sorting algorithm in java. Merge sort is a divide and conquer algorithm - hence it offers a more optimized approach for sorting than the others. The time complexity of mergeSort() function is O(nlogn) while the time complexity of merge() function is O(n) - making the average complexity of the algorithm as O(nlogn). Heap sort, like merge sort, is an optimized sorting algorithm (even though it is not a part of the divide and conquer paradigm). The time complexity of heapify() is O(nlogn) while the time complexity of the heapSort() function is O(n) – making the average complexity of the algorithm as O(nlogn). Selection sort, bubble sort, and insertion sort all have the best case time complexity is O(n) and the worst-case time complexity is O(n2).
Java Sorting Algorithms Cheat Sheet
Here is a cheat sheet for all sorting algorithms in Java:
| Algorithm | Approach | Best Time Complexity |
| Merge Sort | Split the array into smaller subarrays till pairs of elements are achieved, and then combine them in such a way that they are in order. | O(n log (n)) |
| Heap Sort | Build a max (or min) heap and extract the first element of the heap (or root), and then send it to the end of the heap. Decrement the size of the heap and repeat till the heap has only one node. | O(n log (n)) |
| Insertion Sort | In every run, compare it with the predecessor. If the current element is not in the correct location, keep shifting the predecessor subarray till the correct index for the element is found. | O (n) |
| Selection Sort | Find the minimum element in each run of the array and swap it with the element at the current index is compared. | O(n^2) |
| Bubble Sort | Keep swapping elements that are not in their right location till the array is sorted. | O (n) |
Conclusion
Sorting in Java might seem like a difficult concept to grasp for beginners, but it is very rewarding when one gets a concrete understanding of the same. Our list of a few of the most commonly used sorting methods in Java will help you in your preparation. If you are stuck anywhere, our experts will be happy to provide you any type of Java help online.








