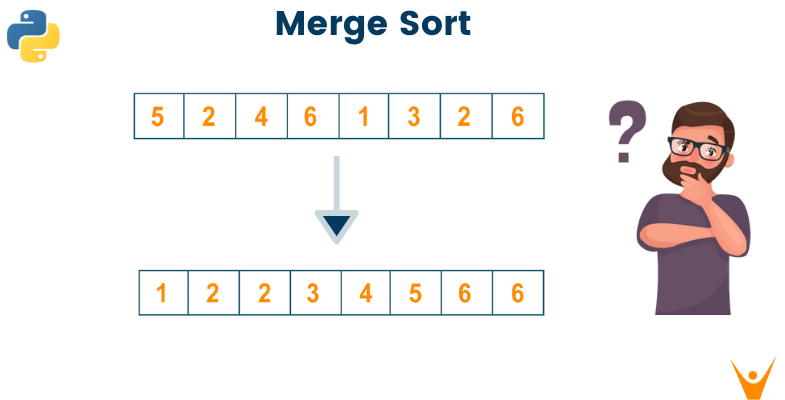
Sorting is a technique to rearrange the collection of data into a specific order.. In this article, we will how the Merge Sort algorithm works using an example along with its Python Program to implement it practically. So, let's get started!
What is Merge Sort?
There are many sorting algorithms possible to sort the data like bubble sort, quick sort, counting sort, etc. All these algorithms have their own techniques to sort the data, along with some advantages and disadvantages. Merge sort is one of these sorting algorithms based on the divide and conquer technique.
The principle working of merge sort is that it divides the list of data into two halves and again calls these subparts to further divide it into two halves. It keeps repeating the process until each subpart of the list contains only one element.
Later, it will join these sub-parts of one element into two elements by sorting them. Again, the subpart containing two elements will be joined with the other two elements after sorting. This process keeps repeating by calling the function recursively until we get the final sorted list of elements.
Merge sort is very popular for its efficiency to sort the data in a small amount of time. It is one of the best examples of applications for divide and conquer approach in Python. If you don't know, Divide and conquer is a famous algorithmic strategy in computer science that involves dividing a problem down into smaller subproblems until the subproblems become simple enough to be addressed directly.
Algorithm for Merge Sort
The divide and conquer approach to sorting n numbers using merge sort consists of separating the array T into two parts where the sizes are almost the same. These two parts are sorted by recursive calls and then merged with the solution of each part while preserving the order.
The algorithm considers two temporary arrays U and V, into which the original array T is divided. When the number of elements to be sorted is small, a relatively simple algorithm is used. ‘mergeSort’ separates the instance into two halves sized sub instances, solves them recursively, and then combines the two sorted half arrays to obtain the solution to the original instance.
Merge(U[1,....,m+1], V[1,....,n+1], T[1,....,m+n]) i,j <- 1 U[m+1], V[n+1] <- infinite for k <- 1 to m+n do if U[i] < V[j] then T[k] <- U[i]; i <- i + 1 else T[k] <- V[j]; j <- j + 1 mergeSort(T[1,....,n]) if n is sufficiently small then insert(T) else array U[1,...1+(n/2)], V[1,....1+(n/2)] U[1,...(n/2)] <- T[1,...(n/2)] V[1,...(n/2)] <- T[(n/2)+1,...n] mergeSort(U[1,...(n/2)]) mergeSort(V[1,...(n/2)]) Merge(U, V, T)
Merge Sort Example
Here we take the given unsorted list of elements.
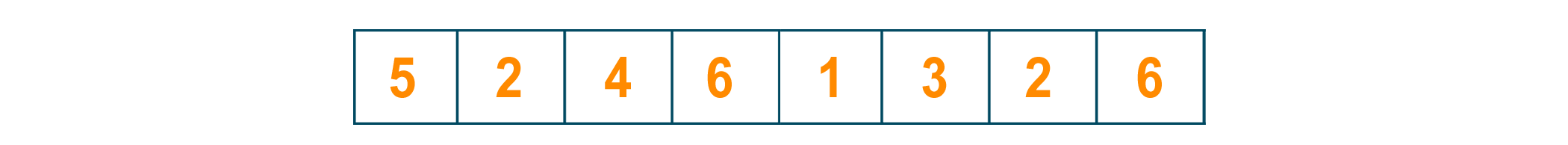
We divide it into two halves as given below

We keep dividing it until the subpart of the list consists of only one element

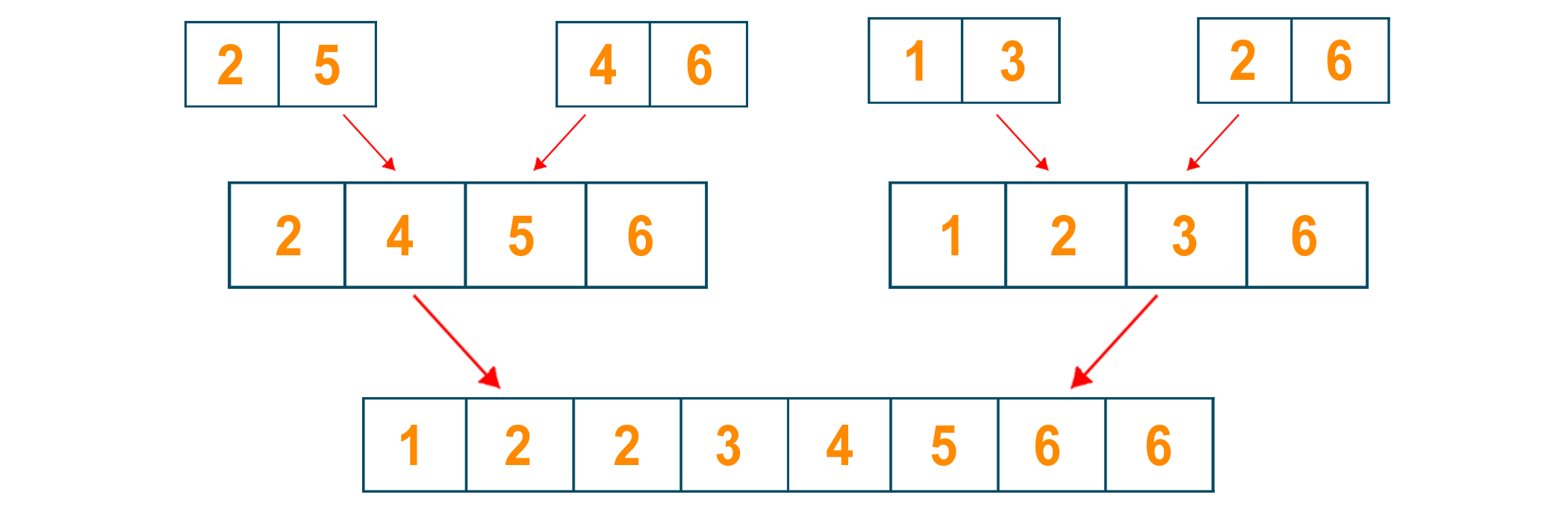
Later, we will combine the two elements in the given sorted manner

Again, we will combine the two lists of two elements and convert them into a list of four elements after sorting. We will keep repeating the process until we find the final sorted sequence of the array
The final sorted sequence of data is given
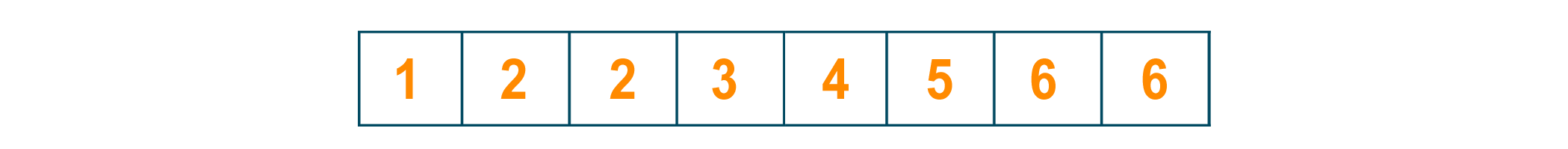
Python Program For Merge Sort
We have given the complete Python program to implement Merge Sort:
def mergeSort(arr): if len(arr) > 1: a = len(arr)//2 l = arr[:a] r = arr[a:] # Sort the two halves mergeSort(l) mergeSort(r) b = c = d = 0 while b < len(l) and c < len(r): if l[b] < r[c]: arr[d] = l[b] b += 1 else: arr[d] = r[c] c += 1 d += 1 while b < len(l): arr[d] = l[b] b += 1 d += 1 while c < len(r): arr[d] = r[c] c += 1 d += 1 def printList(arr): for i in range(len(arr)): print(arr[i], end=" ") print() # Driver program if __name__ == '__main__': arr = [0,1,3,5,7,9,2,4,6,8] mergeSort(arr) print("Sorted array is: ") printList(arr)
Output:
0,1,2,3,4,5,6,7,8,9
Time and Space Complexity
The running time complexity for best-case, worst-case, and average-case scenarios is O(n*log n) where n is the number of elements to be sorted. The space complexity of the algorithm is O(n) where we need an array of size n to place the sorted element.
Why Is Merge Sort Fast?
Because of its efficiency in handling huge datasets, Merge Sort is recognized to be the fastest algorithm in Python.
Python's built-in sort() function uses Timsort, a Merge Sort version optimized for the peculiarities of Python's data types and memory model. Timsort makes use of the fact that Python's lists are implemented as dynamic arrays, allowing them to be resized as needed. Timsort achieves high performance even on very big datasets by dynamically resizing the arrays during the merge process.
It is considered quick because it is a "divide-and-conquer" algorithm, which means that it divides the problem into smaller sub-problems that are easier to solve. As a result, the algorithm can operate on fewer bits of data at a time, reducing overall time complexity.
Another reason for considering it is fast because it employs a technique known as "sorting by merging." Two sorted arrays are joined into a single sorted array using this technique. This procedure is done indefinitely until the full dataset has been sorted.
The approach can take advantage of the fact that merging two already-sorted arrays is a relatively fast process by dividing the problem down into smaller chunks and sorting them independently.
Advantages & Disadvantages of Merge Sort
The biggest advantage of Merge sort is that it can sort large data sets easily because it has faster time complexity. It is also a stable sorting algorithm which means it maintains the relative order of equal elements. Also, merge sort works when sorting linked lists because of its divide-and-conquer approach.
But there are some limitations as well. First, merge sort requires an array of the same size as the original list to store the final sorted array which consumes the large memory space. It is also slower when it comes to sorting smaller data sets.
Overall, it is an amazing sorting algorithm that is used in different domains of the industry. It is a part of many programming languages, libraries, and frameworks for sorting because of its efficiency. A sector which it is a big part of is Database Systems for query processing, result merging, and indexing. It is also utilized in Google PageRank results, E-commerce algorithm, and External sorting.
Conclusion
Merge Sor is one of the most important sorting algorithms that every programmer must learn and understand how it works. You should also try our Python Program for Merge Sort to practice it yourself. If you find anything difficult, we have expert Python Tutors to teach you online.