In this article, we will study what is recursion and how actually the recursion works. We will also learn the characteristic of recursive function along with some recursive programs which are most frequently asked in the interviews along with their C++ code. So, let’s get started!
What Is Recursion?
Recursion is the process of calling the function by itself as its subroutine to solve the complex program. Recursion uses the method of dividing the program into sub-tasks and calling it repeatedly instead of the iterative method which takes lots of effort and time to solve the same problem. Therefore, the function which calls itself is called the recursive function, and the process of calling a function by itself is called recursion. The most important thing about the recursion is it should have the base case to terminate the recursion. As the recursive function calls itself continuously, it is always possible that the program goes into the infinite loop. So if we create the terminate base case using the if..else statement, the program will check the base case condition every time and prevent going into the infinite loop.
How Does Recursion Work?
The function of the recursion approach is to solve the problem effectively in comparison to another problem-solving approach. The recursion process divides the problem into the subtask as a function and continuously calls the same function again to get one step closer to the final solution. This process continues until we find the final solution to the problem. Each time the part of the solution is found, it is stored in the form of stack data structure in the memory and at last, popped out to get the final solution. As we approach the final solution, there is a base condition that should be checked to get out of the recursion process. This base condition is checked using the conditional statement and hence avoids the recursion process to get into the infinite loop. If for any reason the base case fails to work, the program will fall into an infinite loop and we will never reach the solution of the program. Below is the working of recursion in C++.
void recursion() { ... .. ... recursion(); ... .. ... } int main() { ... .. ... recursion(); ... .. ... }
The figure below shows how recursion works by calling the recursive function again and again.
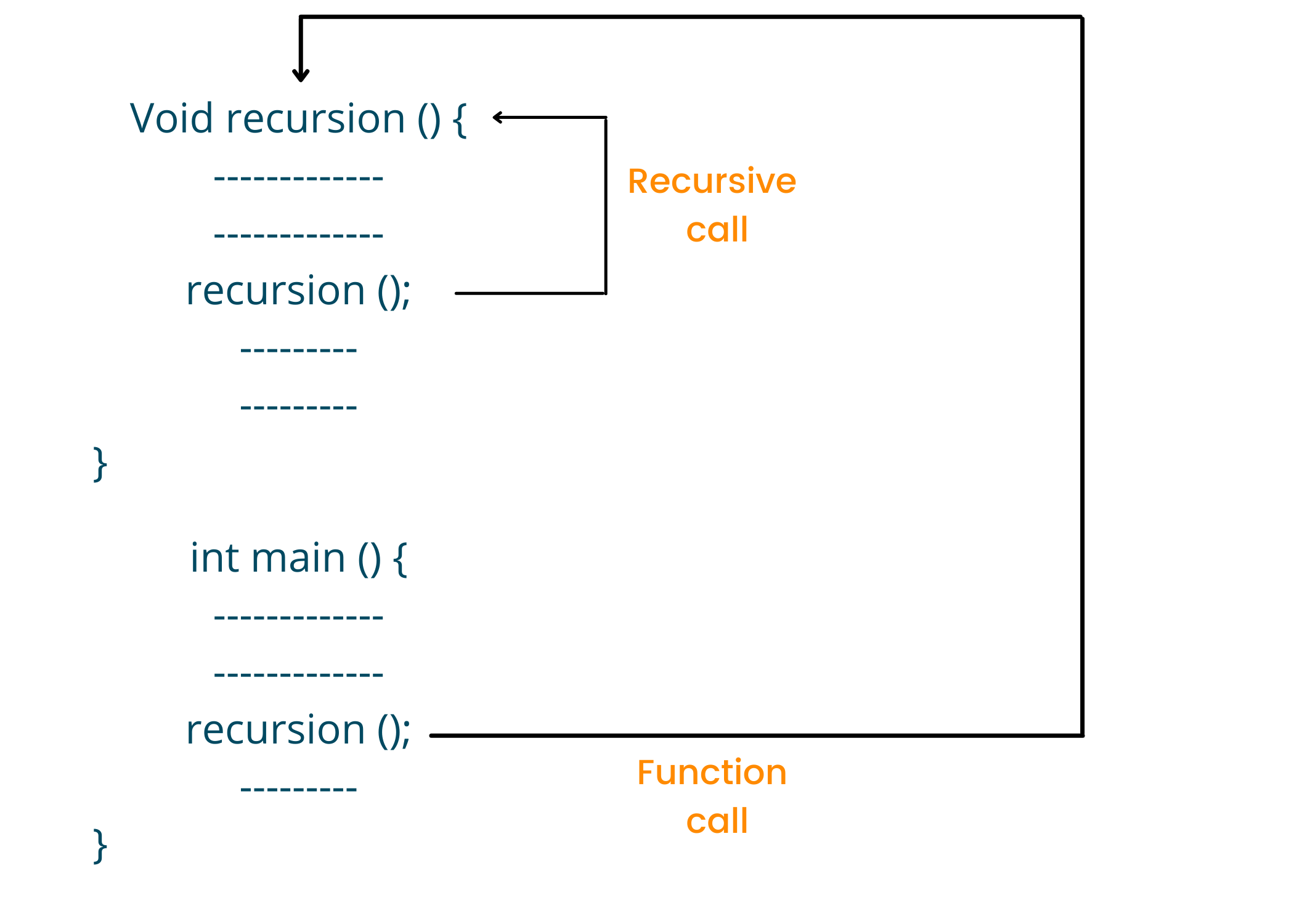
There are two types of recursive function i.e. direct recursion and indirect recursion. Direct recursion is when the function calls itself just like we saw in the above program. Indirect recursion is when the function calls another function and then that function calls the calling function.
Advantages of C++ Recursion
- Less number code lines are used in the recursion program and hence the code looks shorter and cleaner.
- Recursion is easy to approach to solve the problems involving data structure and algorithms like graph and tree
- Recursion helps to reduce the time complexity
- It helps to reduce unnecessary calling of the function
- It helps to solve the stack evolutions and prefix, infix, postfix evaluation
- Recursion is the best method to define objects that have repeated structural forms
Disadvantages of C++ Recursion
- It consumes a lot of stack space
- It takes more time to process the program
- If an error is accrued in the program, it is difficult to debug the error in comparison to the iterative program.
The recursion approach is the most important method to solve any program and therefore, there are many popular problem statements which are asked in technical interviews to test your level of understanding of the concept of recursion.
Top 5 Recursion C++ Examples
Below, we will study some of that recursive programs as an example along with their C++ code.
1) Fibonacci Series Using Recursion in C++
Fibonacci number series is the sequence of numbers such that each number is the sum of the two preceding ones starting from zero(0) and one(1).
C++ program
#include <iostream> using namespace std; int fibonnaci(int x) { if((x==1)||(x==0)) { return(x); }else { return(fibonnaci(x-1)+fibonnaci(x-2)); } } int main() { int x , i=0; cout << "Enter the number of terms of series : "; cin >> x; cout << "\nFibonnaci Series : "; while(i < x) { cout << " " << fibonnaci(i); i++; } return 0; }
Output
Enter the number of terms of series : 15
Fibonnaci Series : 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
Here in the above program, the "fibonacci" function is the recursive function which calls itself and finds the Fibonacci series.
The time complexity by the recursive Fibonacci program is O(n^2) or exponential.
2) Factorial Program Using Recursion In C++
Factorial is the product of an integer and all other integers below it. For example, the factorial of 5 (5!) is equal to 5x4x3x2x1 i.e. 120.
C++ program
#include <iostream> using namespace std; int fact(int n); int main() { int n; cout << "Enter a positive integer: "; cin >> n; cout << "Factorial of " << n << " = " << fact(n); return 0; } int fact(int n) { if(n > 1) return n * fact(n - 1); else return 1; }
Output
Enter an positive integer: 6
Factorial of 6 = 720
Here the recursive function "fact" will take a number as a parameter for which we want to find the factorial. And then recursively call the function until the base condition becomes true which is when the number as a parameter becomes 1.
The time complexity for the recursive factorial program is O(n) because only one loop is executed at a time while finding the factorial of the number using the recursive function. Also, there is no extra space required during recursive calls and therefore, the space complexity is also O(n).
3) Program To Calculate Number Power Using Recursion In C++
In this program, we will calculate the power of the number using the recursion approach where the base and exponent is taken as input by the user.
C++ Program
#include <iostream> using namespace std; int calculate(int, int); int main() { int base, power, result; cout << "Enter base number: "; cin >> base; cout << "Enter power number(positive integer): "; cin >> power; result = calculate(base, power); cout << base << "^" << power << " = " << result; return 0; } int calculate(int base, int power) { if (power != 0) return (base*calculate(base, power-1)); else return 1; }
Output
Enter base number: 3
Enter power number(positive integer): 4
3^4 = 81
Here the recursice function "calculate" calls itself again and again with the base condition to check the power until 0 because the exponent is always the positive integer.
The running time complexity for the program to find the power of the number using recursion is O(logn) because every time the recursive function is called, the parameter of the next call is increased by exponential times. Therefore, the time complexity is the function of the log.
4) Reverse A Number Using Recursion In C++
In this program, we will take input from the user as an integer number and reverse it using the recursive function.
C++ program
#include <iostream.h> using namespace std; int reverseNumber(int n) { static temp,sum; if(n>0){ temp = n%10; sum = sum*10 + temp;
reverseNumber(n/10); } else { return sum; } } int main() { int n,reverse; cout<<"Enter number"; cin >> n; reverse = reverseNumber(n); cout << "Reverse of number is" << reverse; return 0; }
Output
Enter number : 3456
Reverse of number is : 6543
In this program, we will recursively call the "reverseNumber" function with the parameter that the user entered.
The running time complexity of the program is O(log(n)) because every time the function is called recursively, it takes 1/10 of the number as a parameter for the next call. Therefore, the time complexity for reversing the number using the recursive function is O(log(n)).
5) Checking Whether The Number Is Prime Or Not Using Recursion In C++
A prime number is a number that is divisible only by itself and 1. In this program, we will check whether the given number is a prime number or not.
C++ program
#include <bits/stdc++.h> using namespace std; bool isprime(int n, int i = 2) { if (n <= 2) return (n == 2) ? true : false; if (n % i == 0) return false; if (i * i > n) return true; return isprime(n, i + 1); } int main() { int n = 18; if (isprime(n)) cout << "Yes, Number is Prime Number"; else cout << "No, Number is not Prime Number"; return 0; }
Output
No, Number is not Prime Number
Here, we create the recursive function "isprime" and all it recursively and then check the prime number condition using conditional statements.
The running time complexity of the program to check whether the number is prime or not is O(sqrt(n)) because when we recursively call the function isPrime we check whether it is less than the square root of the given number.
Conclusion
Even though the recursion approach consumes a lot of memory storage because of the use of stack data structure, it is widely used to solve various problem statements to reduce the time complexity and lines of codes in the program. Check out one such application of the recursive function to reverse the linked list. It is one of the most frequently asked interview questions while clearing the technical rounds and hence, it is recommended to have a strong understanding of the recursion concept.
