Binary trees are fundamental data structures in computer science, allowing efficient storage and retrieval of data. Traversing a binary tree is a common operation that provides insights into the tree's structure and contents. In this article, we will explore the concept of reverse-level order traversal of a binary tree, understand its algorithm, and provide a detailed, non-plagiarized explanation.
Reverse Level Order Traversal
Reverse level order traversal is a variation of the regular level order traversal, where we traverse the binary tree level by level from right to left instead of left to right. In other words, we start traversing from the deepest level (the last level) and move upwards toward the root level. This traversal helps us explore the binary tree in a bottom-up fashion.
Let's visualize the reverse level order traversal with an example binary tree:
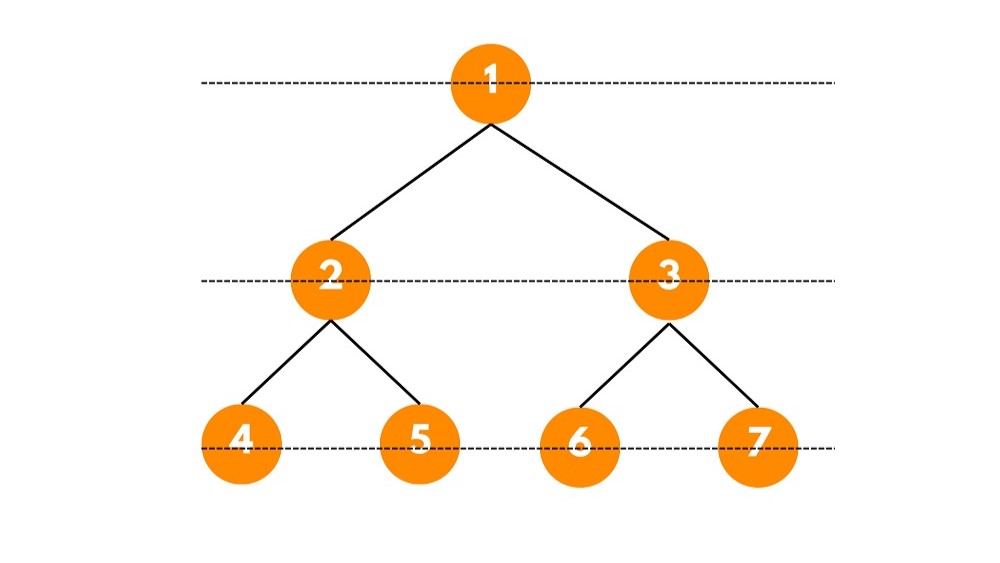
The reverse level order traversal of this binary tree will be: 4 -> 5 -> 6 -> 7 -> 2 -> 3 -> 1
Let us explore the approaches to solve the reverse level order of a binary search tree.
Iterative BFS Method for Reverse Order Traversal
The Iterative Breadth-First Search (BFS) method for reverse order traversal is a clever approach to traverse a BST from the deepest level (rightmost nodes) to the root level in reverse. It utilizes a queue data structure to keep track of nodes at each level while traversing the tree. By processing the nodes in a last-in-first-out (LIFO) manner, we achieve the reverse order traversal.
The algorithm for the iterative BFS method to achieve reverse order traversal is as follows:
- Create an empty queue to store the nodes for traversal.
- Start with the root node of the BST and enqueue it into the queue.
- While the queue is not empty: a. Dequeue a node from the queue. b. Process or print the value of the dequeued node. c. Enqueue its left child (if exists) and then its right child (if exists).
- Continue the process until all nodes have been traversed in reverse order.
Below is a C++ code implementing the iterative BFS method for the reverse order traversal of a BST:
#include <bits/stdc++.h> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; //iterative bfs void reverseOrderTraversal(TreeNode* root) { if (!root) return; queue<TreeNode*> q; stack<int> reverseTraversal; // Use a stack for reverse order q.push(root); while (!q.empty()) { TreeNode* curr = q.front(); q.pop(); reverseTraversal.push(curr->val); if (curr->right) q.push(curr->right); if (curr->left) q.push(curr->left); } // Print the reverse order traversal while (!reverseTraversal.empty()) { cout << reverseTraversal.top() << " "; reverseTraversal.pop(); } } int main() { // Build the binary search tree as shown in the example TreeNode* root = new TreeNode(10); root->left = new TreeNode(5); root->right = new TreeNode(15); root->left->left = new TreeNode(3); root->left->right = new TreeNode(7); root->right->left = new TreeNode(12); root->right->right = new TreeNode(20); root->left->left->left = new TreeNode(2); root->left->left->right = new TreeNode(4); // Perform reverse level order traversal reverseOrderTraversal(root); return 0;
}
Output:
2 4 3 7 12 20 5 15 10
The time complexity of the iterative BFS approach for reverse level order traversal of a BST is O(N), where N is the number of nodes in the BST. This is because, in the worst case, we need to visit all nodes in the BST once to perform the BFS traversal.
The space complexity of the iterative BFS approach is O(W), where W is the maximum width (maximum number of nodes at any level) of the BST. In the worst case, the queue used for BFS traversal can contain all the nodes at the maximum width level. For a balanced BST, the maximum width would be approximately N/2, and for a skewed BST, the maximum width would be N.
Recursive BFS Method for Reverse Order Traversal
The Recursive Breadth-First Search (BFS) method for reverse order traversal is an innovative approach to explore a BST in a bottom-up manner, starting from the deepest level and moving towards the root level. Unlike the traditional iterative BFS approach that uses a queue, the recursive method utilizes recursive function calls to achieve the reverse order traversal.
The algorithm for the recursive BFS method to achieve reverse order traversal is as follows:
- Perform a recursive BFS traversal of the right subtree (if exists) to explore the deepest nodes first.
- Process or print the current node's value.
- Perform a recursive BFS traversal of the left subtree (if exists) to explore the left children.
- Continue the recursive calls until all nodes have been traversed in reverse order.
Below is a C++ code implementing the recursive BFS method for the reverse order traversal of a BST:
#include <bits/stdc++.h> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; //recursive dfs void reverseOrderTraversal(TreeNode* root) { if (!root) return; // Recur to the right subtree to explore deepest nodes first reverseOrderTraversal(root->right); // Process or print the current node's value cout << root->val << " "; // Recur to the left subtree to explore left children reverseOrderTraversal(root->left); } int main() { // Build the binary search tree as shown in the example TreeNode* root = new TreeNode(10); root->left = new TreeNode(5); root->right = new TreeNode(15); root->left->left = new TreeNode(3); root->left->right = new TreeNode(7); root->right->left = new TreeNode(12); root->right->right = new TreeNode(20); root->left->left->left = new TreeNode(2); root->left->left->right = new TreeNode(4); // Perform reverse level order traversal reverseOrderTraversal(root); return 0; }
Output:
20 15 12 10 7 5 4 3 2
The time complexity of the recursive BFS approach for reverse level order traversal of a BST is also O(N), where N is the number of nodes in the BST. In the worst case, we need to visit all nodes in the BST once to perform the BFS traversal.
The space complexity of the recursive BFS approach is O(H), where H is the height of the BST. In the worst case, the maximum height of the call stack during recursion would be equal to the height of the BST. For a balanced BST, the height would be log(N), and for a skewed BST, the height would be N.








