Counting Sort in Python (with Algorithm & Program)

Sorting is one of the most basic things that every programmer must learn and understand to get a job. In this article, we will study the Counting Sort, its Algorithm, and its implementation in Python. So, let’s get started!

What is Counting Sort?

First, we all know what sorting is. It is the process of ranking elements either in ascending or descending order from the collection of elements. There are many Sorting Algorithms available to sort the data in an array or list and some of them are Bubble sort, Selection sort, Insertion sort, Merge sort, etc.

Counting sort is a sorting algorithm that sorts the elements with the technique of counting the number of occurrences of each unique element in an array or list. It is basically a hashing technique with the keys between a specific range and then counting the number of objects having distinct key values.

We will get the output sequence by doing some arithmetic calculations for positioning each object using its key values. Counting sort uses the partial hashing technique to count the occurrence of the element in O(1). Let us study an example of counting sort for a clear understanding. 

Counting Sort Example

Consider a given array to be sorted. Firstly, we will find the largest element from the array and initialize it as max.

Now we will initialize the new array named count array with length “max+1” with all the elements 0 to store the sorted data.

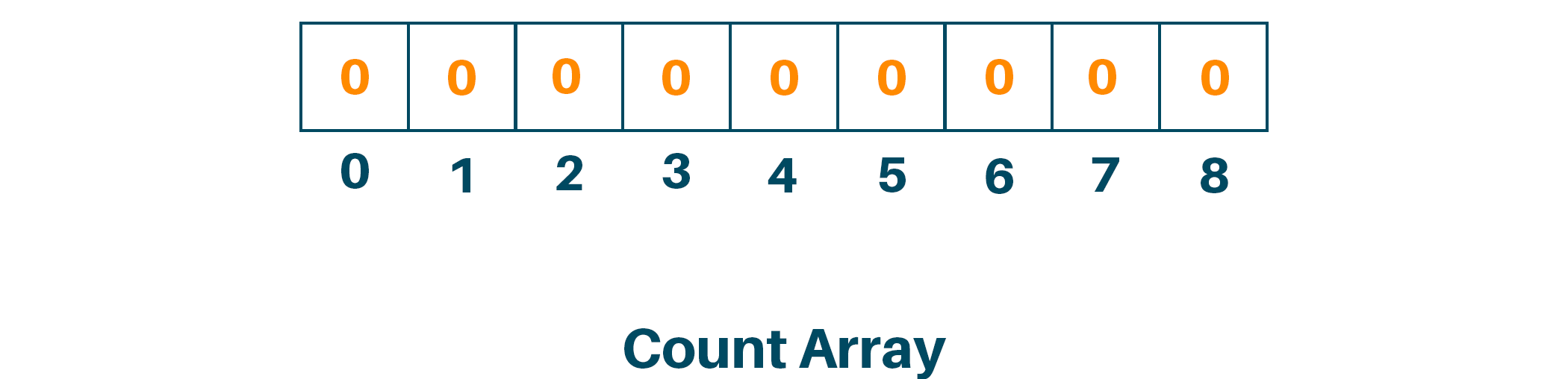
Later, we will store elements of the given array with the corresponding index in the count array as shown in the figure. 

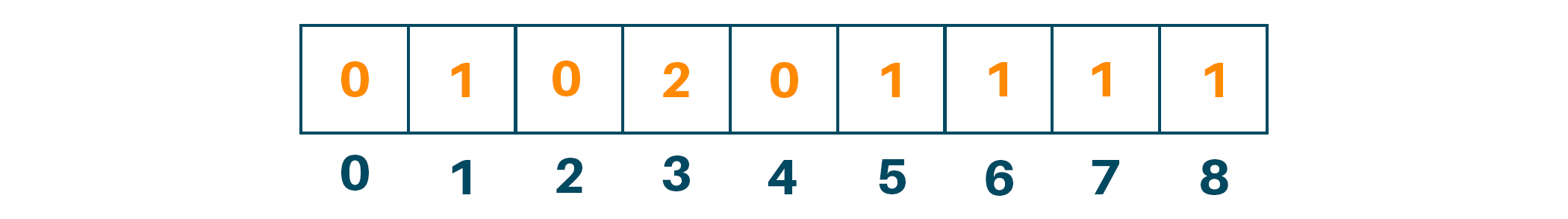
Now, we will modify the count array by adding the previous counts and creating the cumulative sum of an array as shown below:

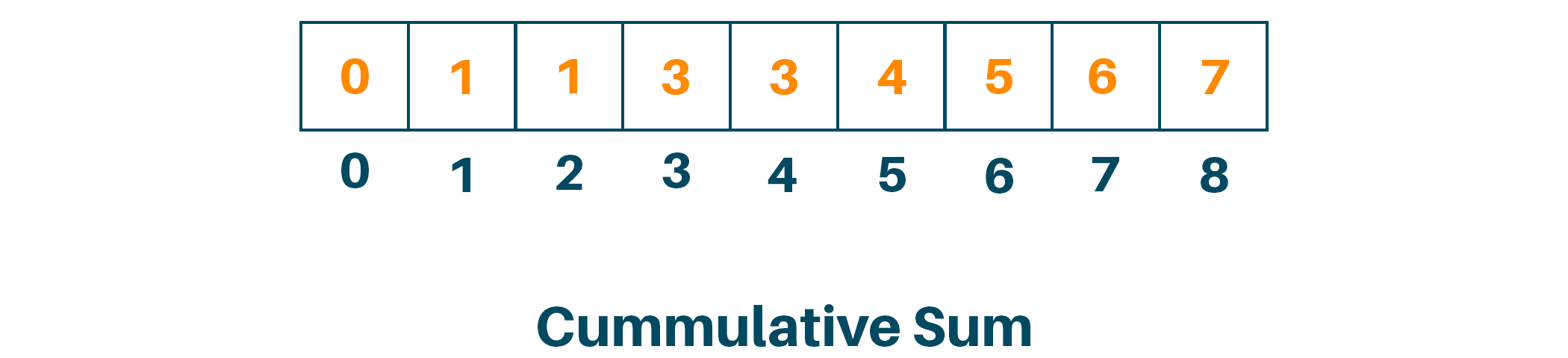
Since we have 7 inputs in the original array, we will create another empty array with 7 places to store the sorted data and place the elements in their correct positions and decrease the count by one.

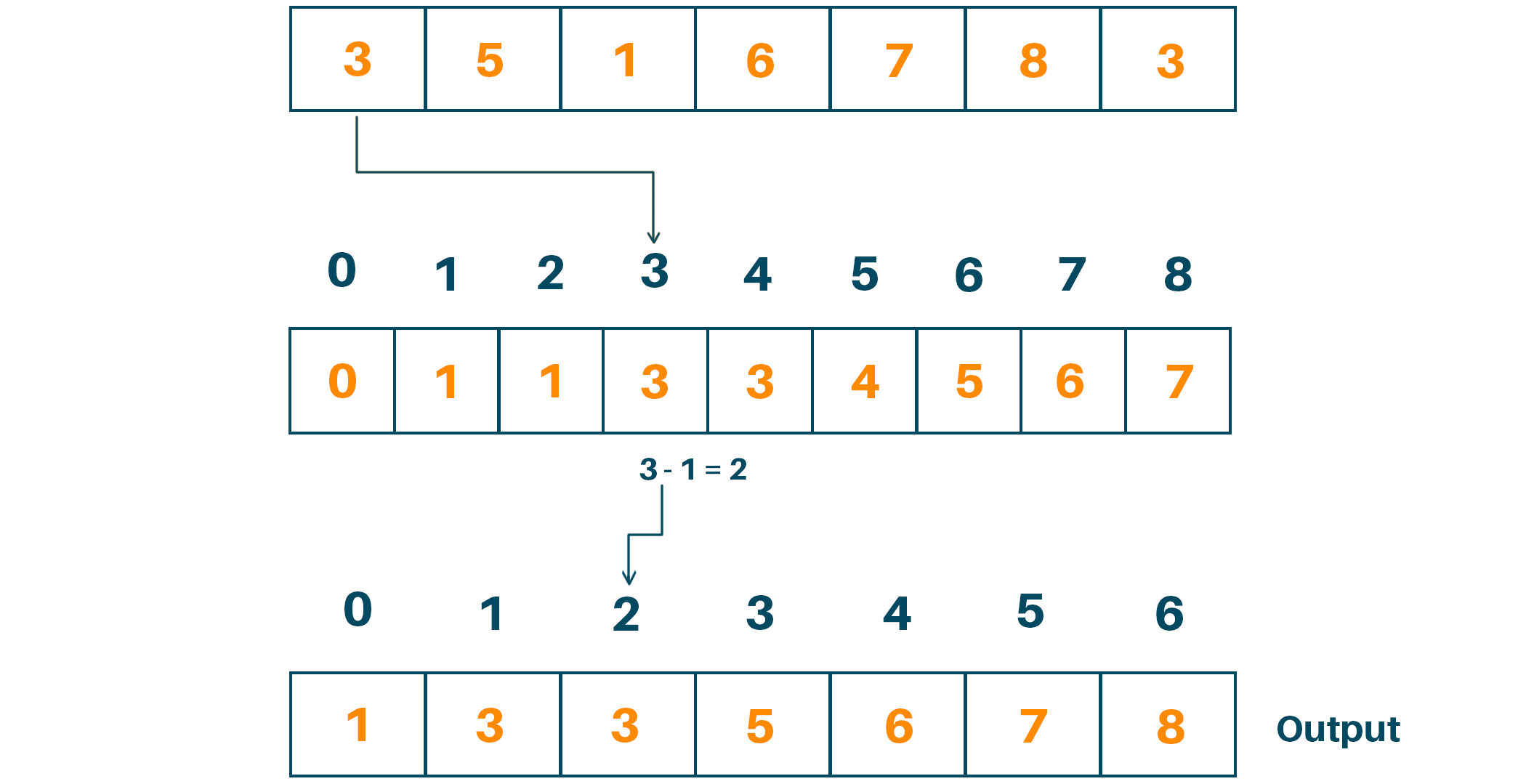
Therefore, the sorted array is:

Algorithm for Counting Sort

Here is the complete algorithm to implement Counting Sort:

countingSort(array, size)

  max <- find maximum element in the array

  initialize count array with all 0s

  for m <- 0 to size

    find the total count of each unique element and

    store the count at mth index in count array

  for n <- 1 to max

    find the cumulative sum and store it in a count array

  for m <- size down to 1

    restore the elements to the array

    decrease count of each element by 1

Python Code for Counting Sort 

Now that you know the algorithm, you can easily do its implementation in Python. Below is the Python code for Counting Sort:

# python program for counting sort

def countingSort(arr):
    size = len(arr)
    output = [0] * size

    # count array initialization
    count = [0] * 10

    # storing the count of each element 
    for m in range(0, size):
        count[arr[m]] += 1

    # storing the cumulative count
    for m in range(1, 10):
        count[m] += count[m - 1]

    # place the elements in output array after finding the index of each element of original array in count array
    m = size - 1
    while m >= 0:
        output[count[arr[m]] - 1] = arr[m]
        count[arr[m]] -= 1
        m -= 1

    for m in range(0, size):
        arr[m] = output[m]

data = [3,5,1,6,7,8,3]
countingSort(data)
print("Sorted Array: ")
print(data)

Output:

Sorted Array:

[1, 3, 3, 5, 6, 7, 8]

Counting Sort Time Complexity

In the above algorithm, we have 4 loops in total. The first loop is to find the largest element in the given array, the second is to store the count of each element. Third loop stores the cumulative sum of each element in the count array and the fourth loop stores the sorted array in the new array using the indexing method of the count array.

The time complexity of the Counting Sort algorithm is O(m+n) where m is the number of elements in the input array and n is the range of input. In all the cases whether it be the best case, worst case, or average case the time complexity of the algorithm is the same because the time complexity of the counting sort algorithm is not dependent on how many elements we store in the array.

Why is Counting Sort not used?

This sorting method has some drawbacks that make it not so useful despite the fact that it is an efficient technique for sorting a restricted range of integer values. The following are some of the main reasons:

• Memory specifications: In order to store the counting array, that has a size proportional to the variety of the input values, the counting sort needs additional RAM. Due to its propensity to quickly run out of memory, the algorithm is inappropriate for large datasets containing a diverse range of input values. 
• Little Application: Counting Only data that fits within a finite range can be sorted. For instance, irrespective of the actual number of elements in the array, if the information is supplied has a maximum value of 100, the counting array is going to have a size of 101. This means that datasets having a range that is too broad or poorly specified cannot be used with the technique.
• Performance: Counting Sort has an O(m+n) time complexity, where m is the input value range and n is the total quantity of elements in the array that is input. Despite having a linear time complexity, the algorithm's performance can suffer with a wide range of input values.

Is Counting Sort space efficient?

The algorithm Counting Sort is not regarded as being space-efficient. The counting array, whose size is proportionate according to the range of input values, requires more memory to be stored. This indicates that the approach is inadequate for huge datasets because its memory consumption grows as the size of the input data does.

The sorting of huge datasets is better suited for algorithms with reduced memory requirements, like Quick Sort and Heap Sort. The number of items in the input array, n, and the range of input values, k, can be used to calculate the space complexity of the counting sort as O(n+k).

Despite having a linear complexity of space, the counting array that must be stored by the algorithm demands additional memory, which may quickly turn into a bottleneck when the input value range is very wide.

Is a Counting Sort stable?

Yes, Counting Sort is a stable algorithm. This indicates that it keeps the input array's equal items' relative positions in the same order. For instance, counting sort will guarantee that x appears before y within the output array if the given input array contains two components x and y that are equal and appear in that order in the input array. 

Practical Applications

The Counting Sort is useful when we have a finite and limited domain of variables. It is also commonly used when the range of input elements is known in advance. This is because it has linear complexity is required.

By comparing the execution time of Counting Sort with other sorting algorithms, one can assess the efficiency and practicality of those algorithms for particular data distributions and ranges.

Conclusion

So far, we have learned Counting Sort in Python with its algorithm an example, and a program. Besides the linear time complexity, it is very useful for finding the smaller integer with multiple counts. Happy Learning :)