Selection Sort in C++ (Code with Example)

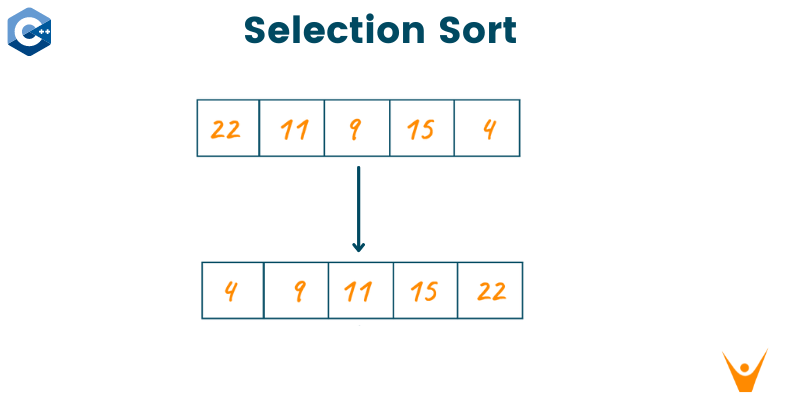
Sorting algorithms take input data in the form of lists of items, conduct specified operations on those lists, and produce an ordered list. Selection sort is a sorting method that uses in-place comparisons to sort data. The array or list is separated into two parts during the selection sort algorithm: the sorted part on the left end and the unsorted part on the right end. The sorted component is initially empty, while the unsorted part is the complete array or list. In this article, we'll look at what selection sort is and how to use it in C++.

What is Selection Sort?

Selection sort is a sorting algorithm that selects the smallest element from an unsorted list and sets it at the beginning of the unsorted list in each iteration. The selection sort algorithm sorts an array by repeatedly choosing the smallest member from the unsorted segment and placing it at the beginning (in ascending order).

Pseudocode for selection sort

selectionSort(array, size)
  repeat (size - 1) times
  set the first unsorted element as the minimum
  for each of the unsorted elements
    if element < currentMinimum
      set element as new minimum
  swap minimum with first unsorted position
end selectionSort

Why is selection sort used?

The following are some uses of  Selection Sort:

• Bubble sort and gnome sort are virtually always outperformed by selection sort.
• When memory writing is a time-consuming procedure, this can be advantageous.
• In terms of the number of writes (0(n)) swaps versus O(n2) swaps), selection sort is preferable to insertion sort.
• It almost always considerably outnumbers the number of writes that cycle sort generates, despite the fact that cycle sort is technically the most efficient in terms of the number of writes.
• This is crucial if writes are much more expensive than reads, as they are in EEPROM or Flash memory, where each write reduces the memory's lifespan.
• In contrast to the Insertion sort, which executes O(n2) number of swaps, the selection sort performs a maximum of n swaps. As a result, when it comes to memory writes, selection sort is less expensive. When compared to other stable sorting algorithms, the sorting approach also gives performance benefits.

How does Selection Sort Algorithm Works?

Let’s understand the working of selection sort step by step with an example:

Step1: Set the array's first element as the minimum.

Step2: Compare the first and second elements. Assign the second element as a minimum if it is smaller than the first.

Step3: Compare the third element to the minimum. If the third element is smaller, assign it as a minimum; otherwise, don’t do any changes. The process continues until the final element of the array.

Step4: Minimum is moved to the front of the unsorted list after each iteration.

Step5: Indexing begins with the first unsorted element in each iteration. Steps are repeated until all the elements are placed at their correct positions.

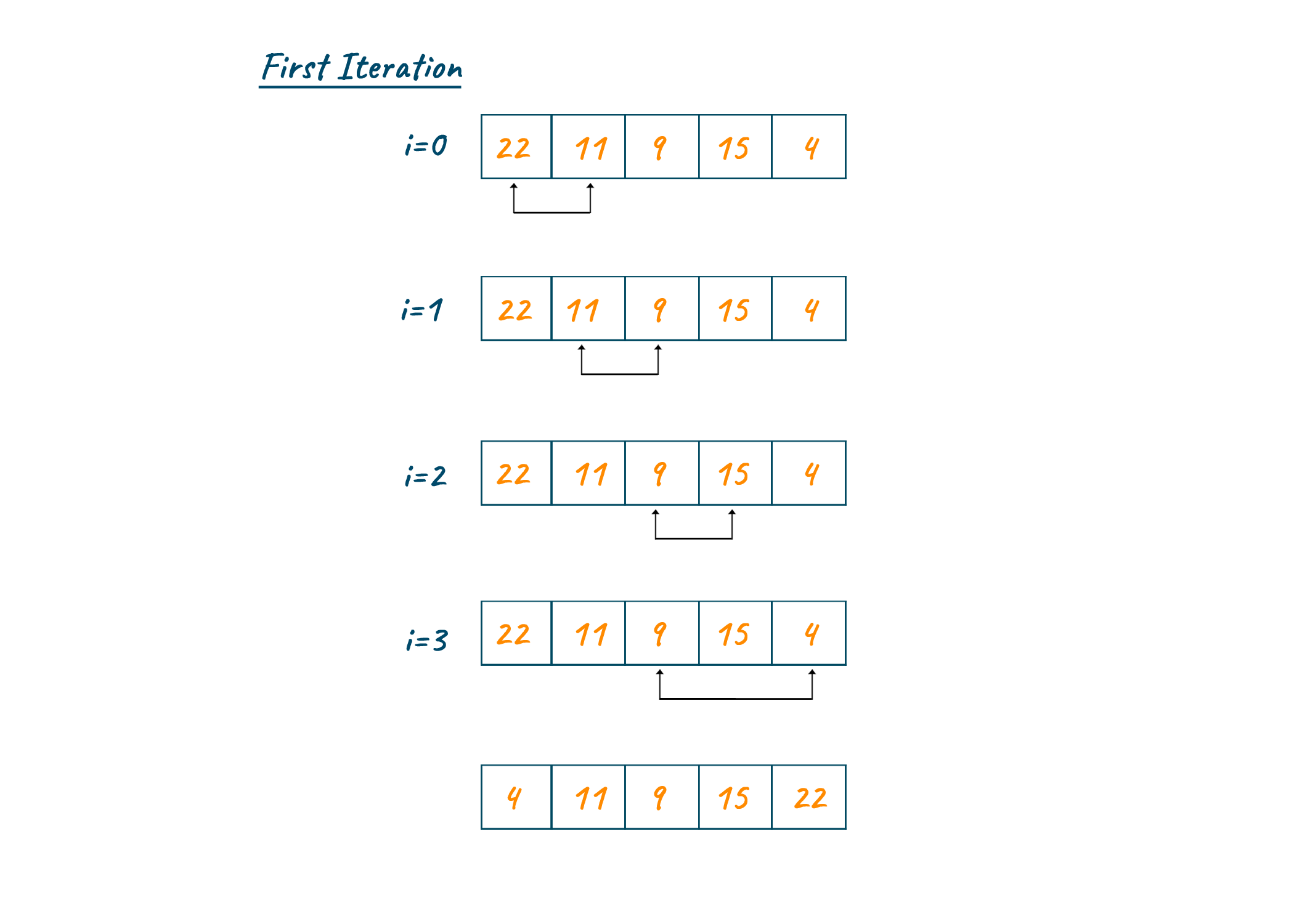
Example:

Looking at the below image you can see that we will compare each element throughout the array and find the first minimum. Assign the first minimum to the first index of an array after the completion of the first pass.

Repeating the same process, we will traverse the array and find the second minimum. Later assign the second minimum to the second index of an array as shown in the below image.

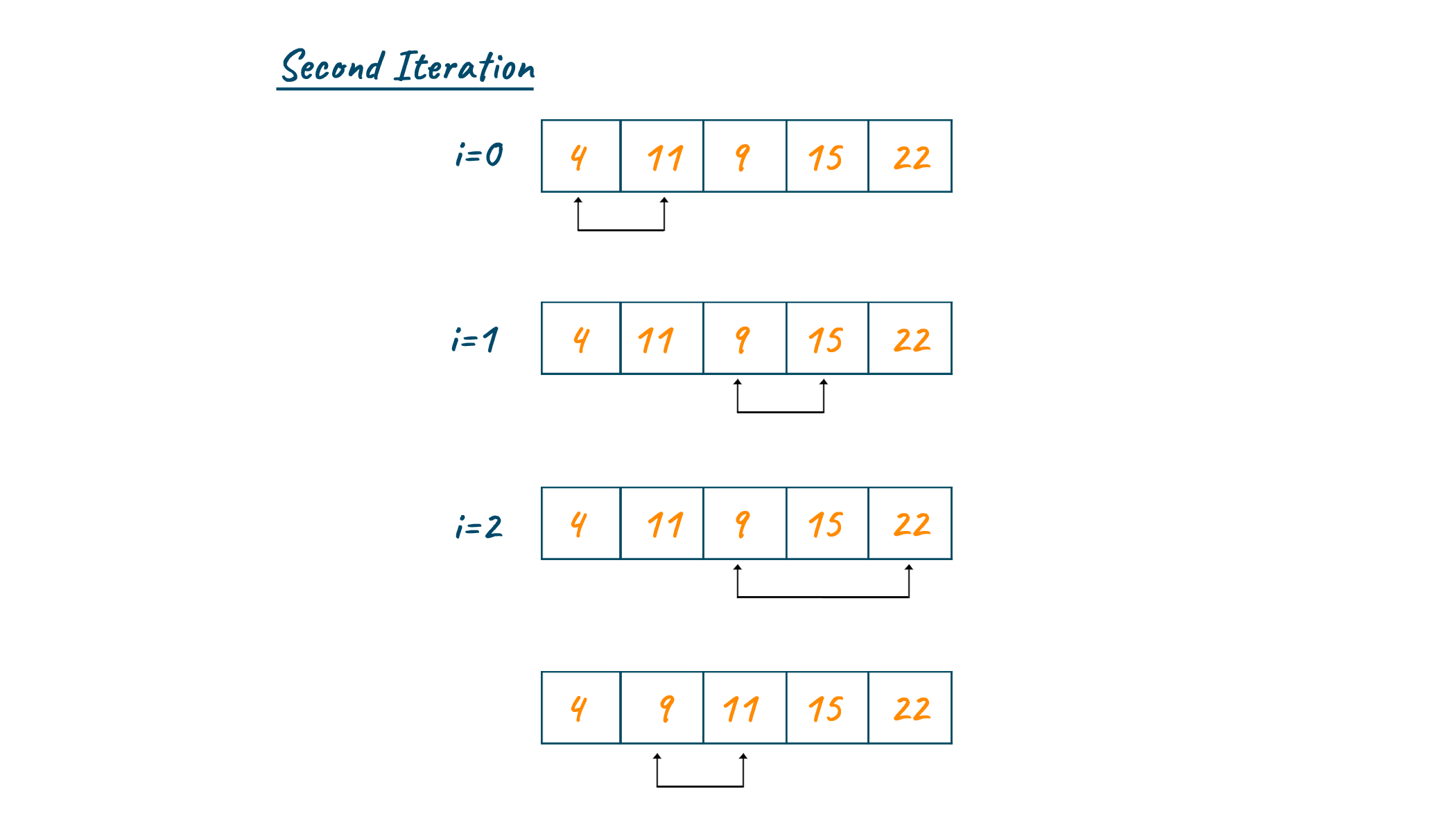
Keep repeating the same process. In our example, the elements are already in the right position and therefore no need for swapping is required.

C++ Program for Selection Sort

Let’s understand the implementation of selection sort in C++ by the following code:

#include<bits/stdc++.h>
using namespace std;
void print(int arr[], int n)
{
    for(int i=0;i<n;i++)
        cout<<arr[i]<<" ";
    cout<<endl;
}
void selectionSort(int arr[], int n)
{
    int i,j,min_in;
    for(i=0;i<n;i++)
    {
        min_in = i;
        for(j=i+1;j<n;j++)
            if (arr[j] < arr[min_in])
                min_in = j;
        swap(arr[i],arr[min_in]);
    }
}
int main(int argv, char* argc[])
{
    int arr[] = {5,4,10,1,6,2};
    int i,j,n,temp;
    n = sizeof(arr)/sizeof(int);
    cout<<"Unsorted Array :";
    print(arr,n);
    selectionSort(arr,n);
    cout<<"Sorted Array :";
    print(arr,n);
    return(0);
}

Output:

Unsorted Array :5 4 10 1 6 2 
Sorted Array :1 2 4 5 6 10

Time Complexity of Selection Sort

Following are the time complexities associated with selection sort:

1. Best Case Complexity - It occurs when there is no need to sort the array because it is already sorted. The time complexity of selection sort in the best-case scenario is O(n2).
2. Average Case Complexity -It happens when the array elements are in a jumbled sequence that isn't ascending or descending properly. The temporal complexity of the selection sort in the average scenario is O(n2).
3. Worst Case Complexity -This comes in the picture when the array elements must be sorted in reverse order. Assume you need to sort the array elements in ascending order, but the elements themselves are sorted in descending order. The selection sort's worst-case time complexity is O(n2).

Conclusion

In summary, we've gone over selection sort in great detail in this article, including how to implement it in C++. It is another sorting approach that can be easily implemented. The principle of the selection sort is to find the smallest element in the array and place it in the correct position every time. When the range of the values to be sorted is known, selection sort works best. As a result, while using selection sort to sort data structures, we can only sort data structures that are linear and finite in size.