Sorting techniques help you arrange the given objects in a specific order. Today we are going to learn one of these sorting techniques, Insertion Sort in Java. While playing a game of cards with your friends, after the cards get distributed, you arrange them in order. How do you do that? Which sorting technique do you use?
What is Insertion Sort?
Insertion sort is a comparison-based sorting algorithm that inserts each element at its correct position in a single journey or iteration. First, the sorted part contains only the first element, while the rest of them are in the sorted part. We then iterate through the unsorted by taking one element at a time and inserting it into its correct position in the sorted part.
This works in the same way as how we arrange the cards in the game. We can also understand from the example of boxes where you need to arrange boxes having different numbers written on them according to the numbers on them. We will use the insertion sort algorithm here.
We assume that the first box is already at its position (or sorted) and then we start from other boxes which aren't at their position according to the prescribed position. If the number on that box is greater than the no. on the box which is sorted it is placed on the right of that box otherwise left. This way, each unsorted box is compared with sorted boxes and put in its right position.
How does Insertion Sort work?
Given with an array say arr of size 4. We need to sort this array using the insertion sort algorithm. Remember that in each journey we put each element at its correct position. And we already assume that the first element i.e. element at the 0th index is already at its correct position.
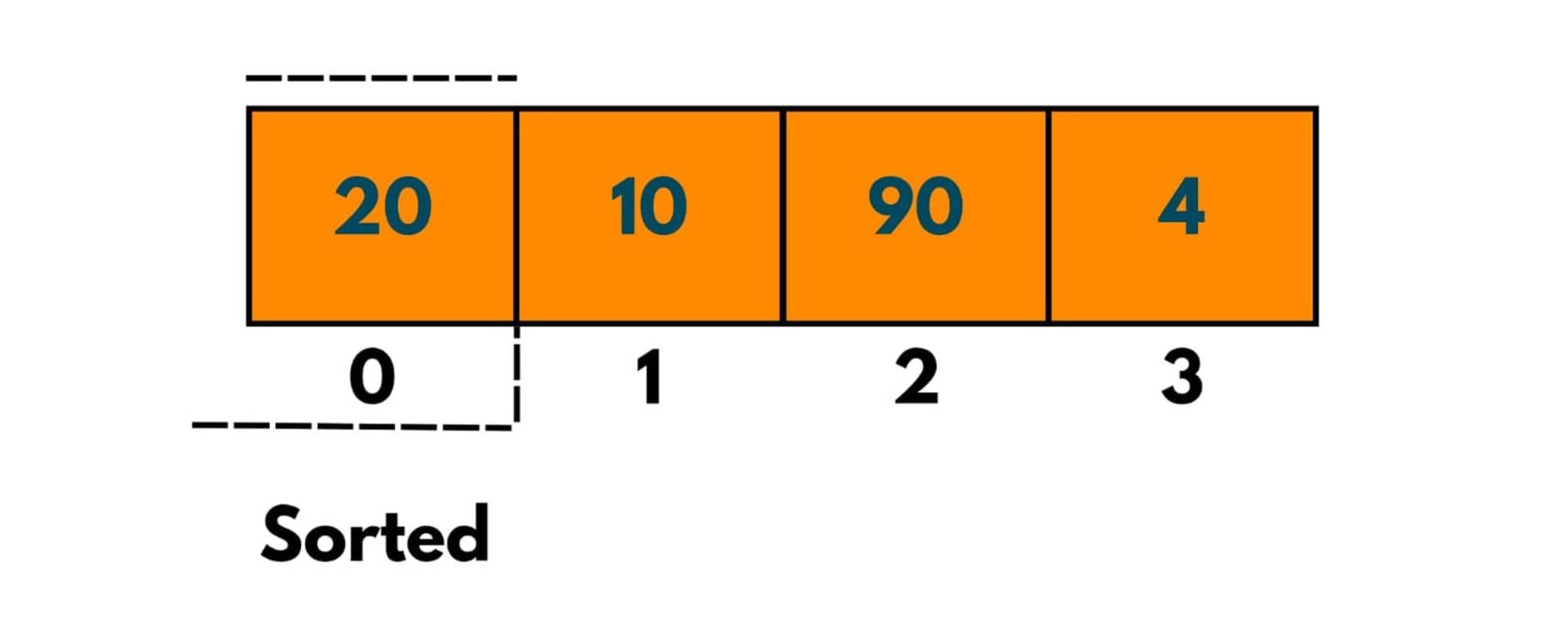
Journey 1: The element next to the last sorted element, i.e. element at index 1 is compared with each element in the sorted part, so as only 1 element exists in the sorted part, the Element at index1 will be compared to the Element at index0.
Pass 1:
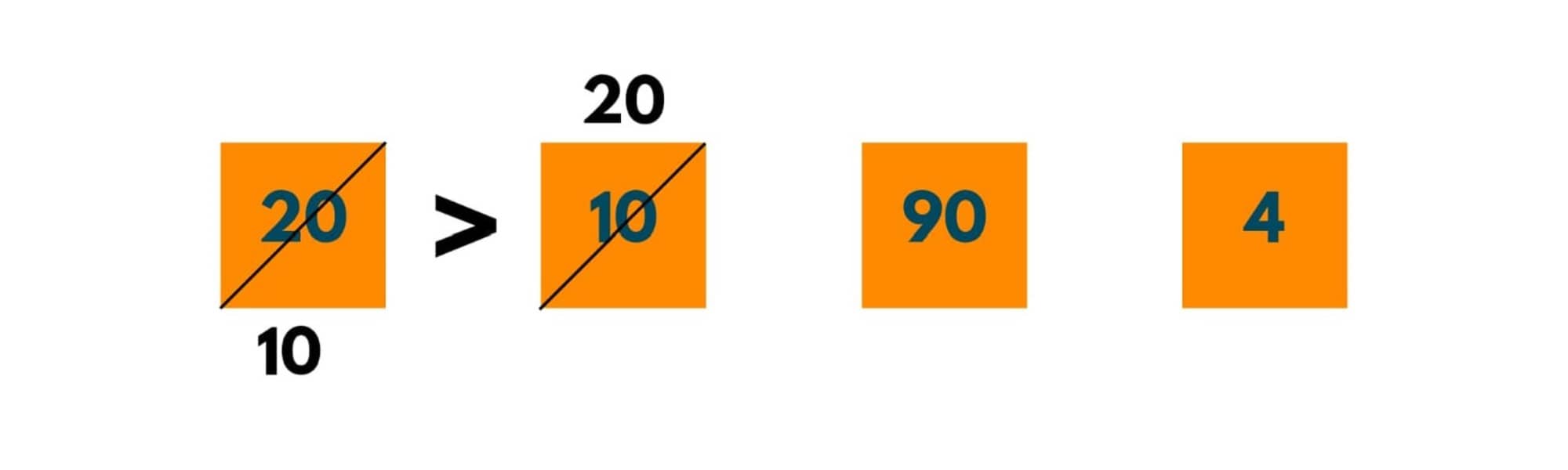
We store the element to be compared as Ele. Here Ele (or 10) < 20, therefore we swap 10 and 20. But as there is no other element except 20 in the sorted part, we stop.
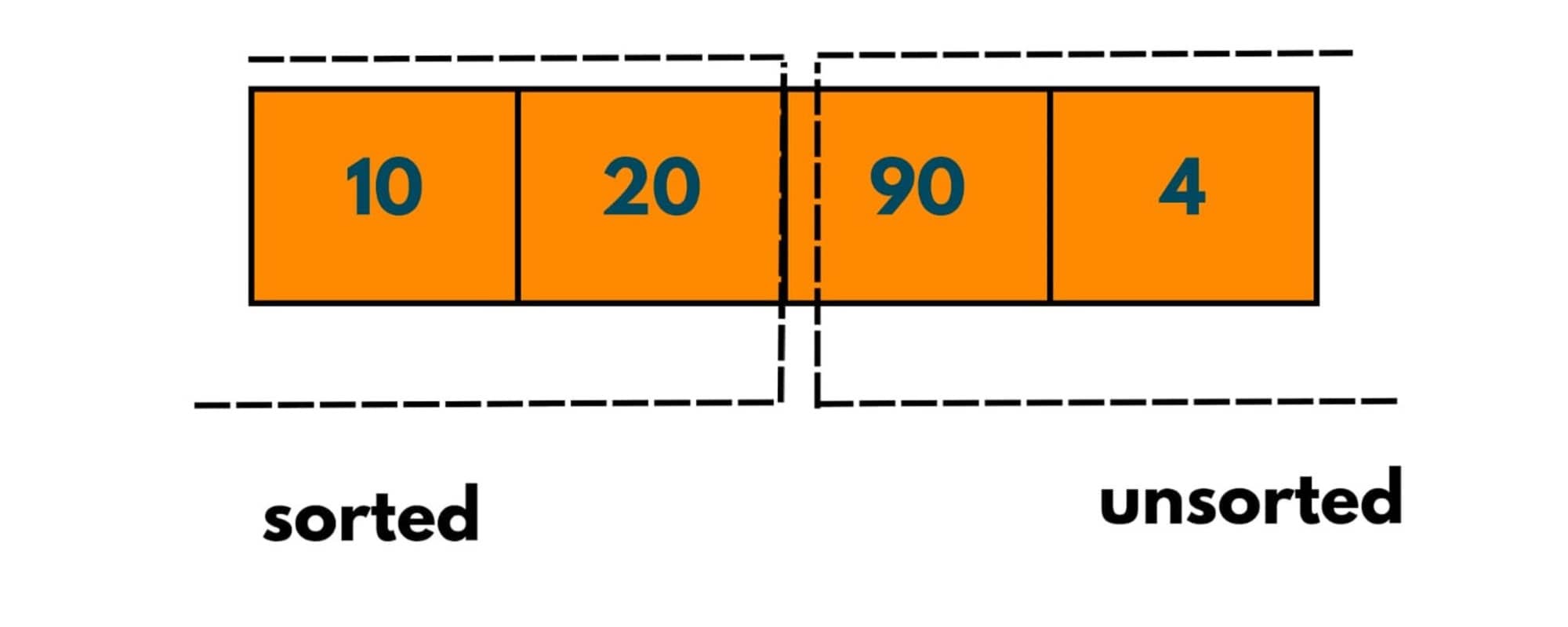
And 2 elements have been sorted. Notice for each Ele or element in an unsorted array, at max no. of passes = no. of comparisons with Ele with sorted elements.
Journey 2:
Pass 1:
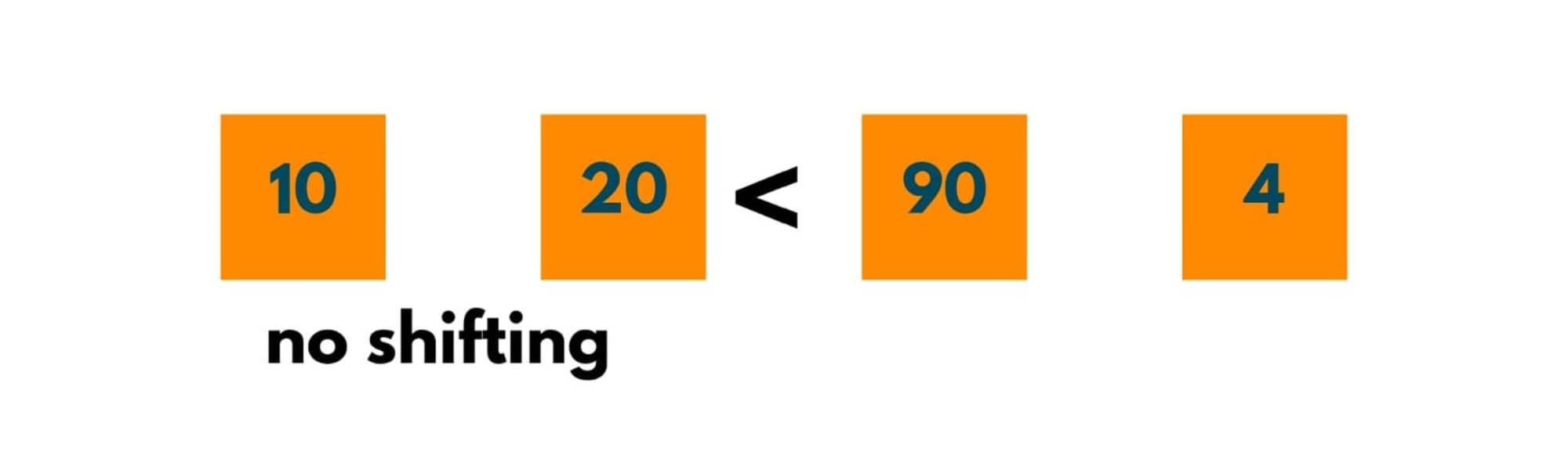
As 90 > 20, implies that 90 is at its correct position and no more comparisons are done. Therefore no. of comparisons = 1.
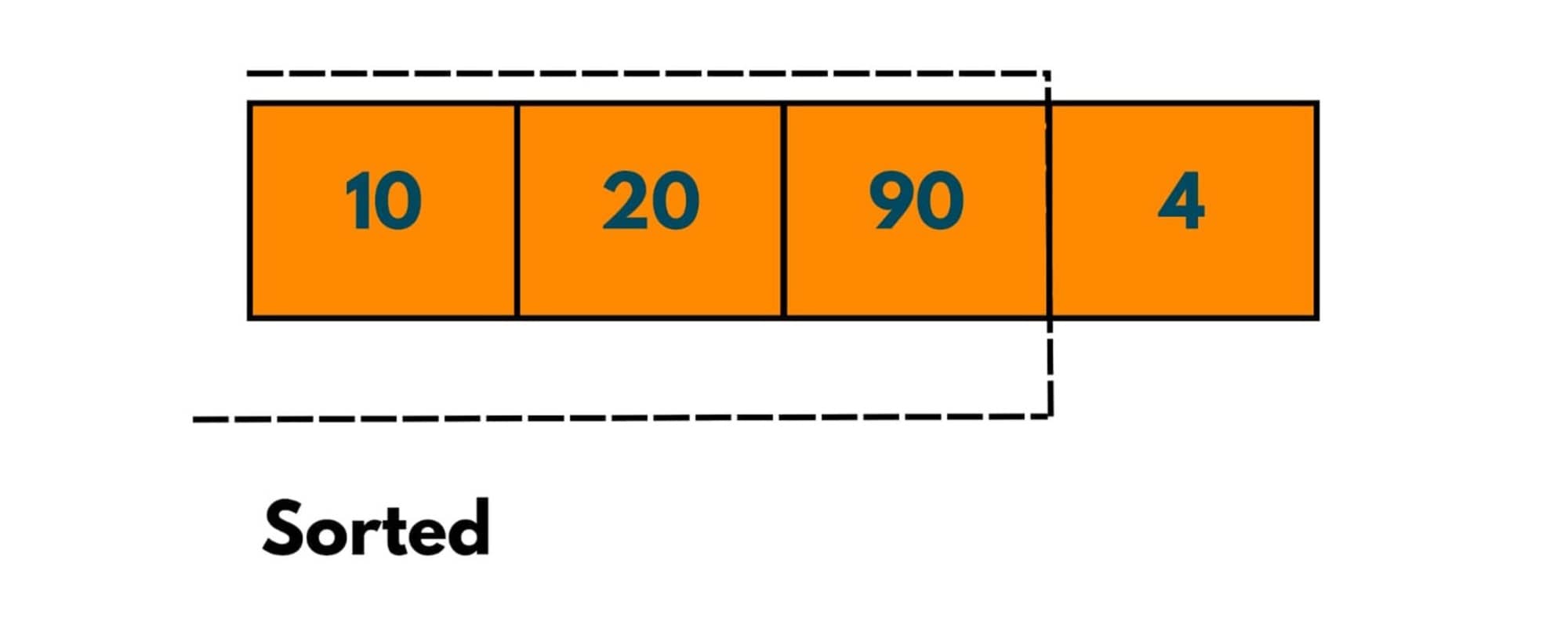
3 elements have been sorted after journey 3. We notice that in each journey we place an element at its correct position. Therefore journeys needed to put these 4 elements at the correct position is 3, i.e. no. of elements in array -1. We used -1 as we initially assumed 1 element to be sorted.
Journey 2:
Pass 1:
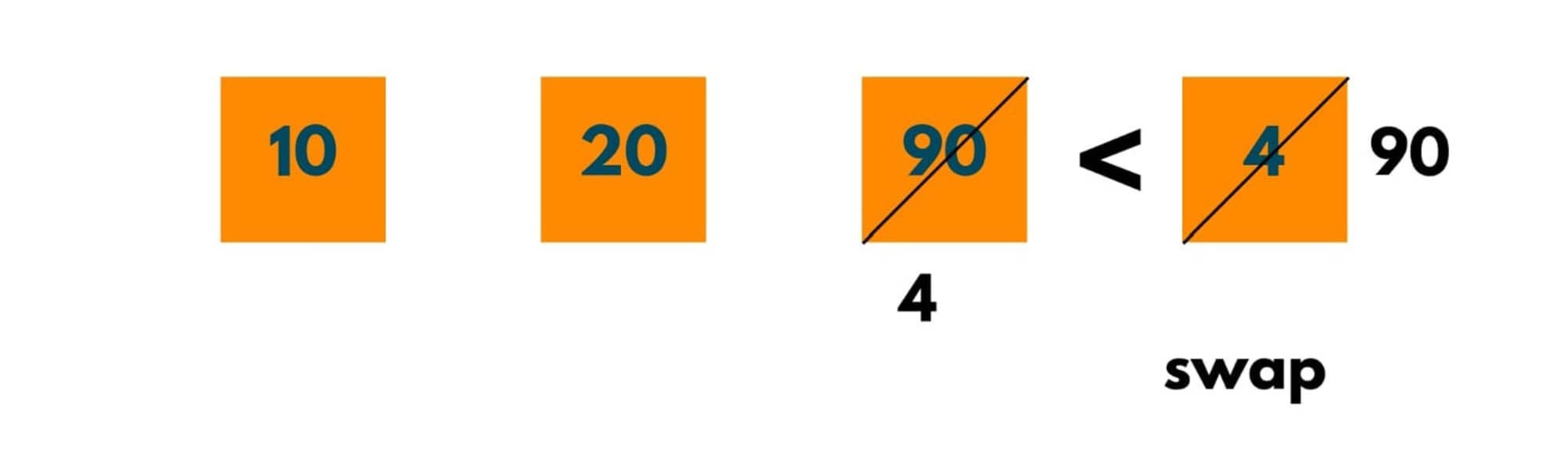
The next element to be compared is 4. As 4 < 90, swapping happens.
Pass 2:
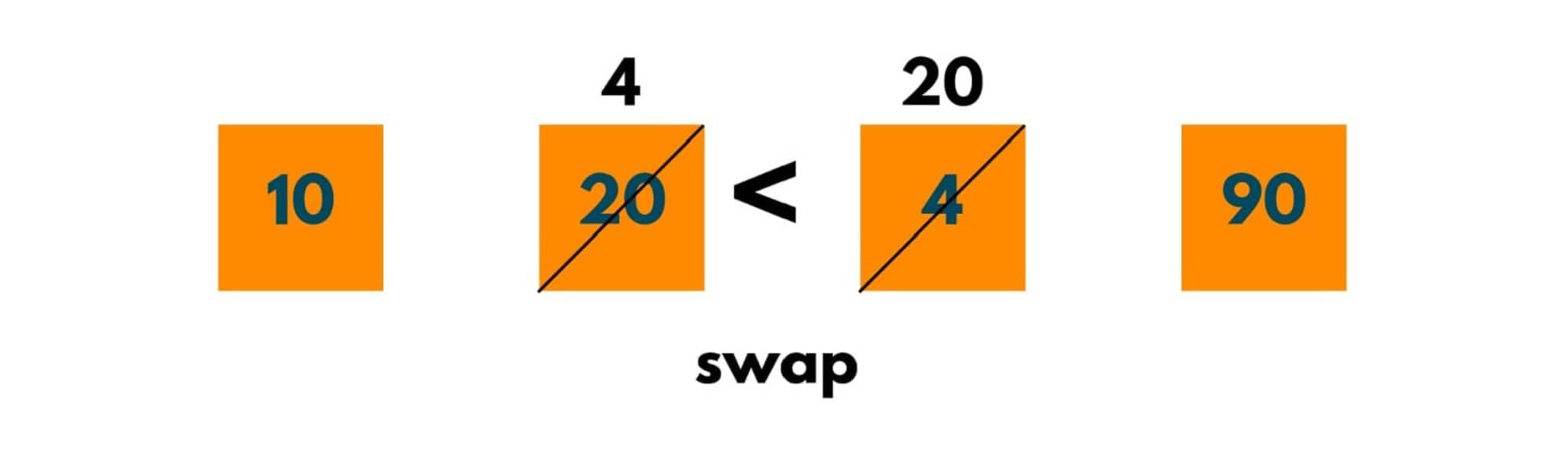
As 4 < 20, swapping happens.
Pass 3:
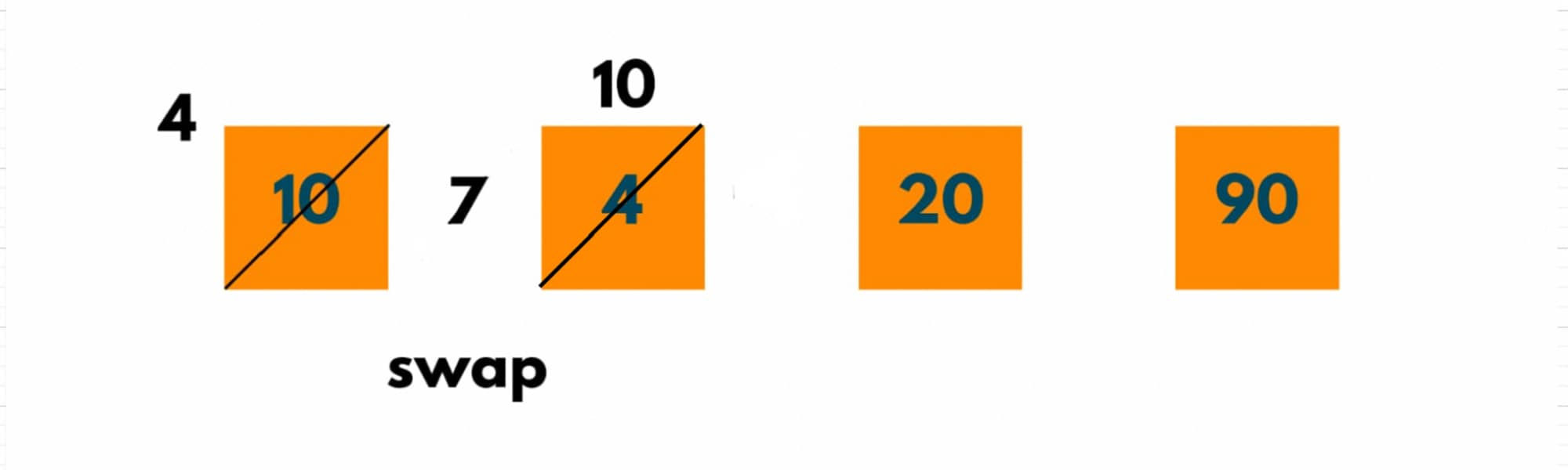
As 4 < 10, swapping happens.
Now all the journeys and no. of passes have been completed and we notice that we are left with the sorted array. Please note these 3 points every time:
- We assume 1st element to always be sorted.
- No. of Journeys = no. of elements - 1.
- No. of passes = Elements in sorted part.
Iterative Insertion Sort Algorithm in Java
Here is the algorithm for insertion sort with the iterative approach in ascending order:
- Run an outer for loop, say i, that keeps track of no. of journeys. It basically points to an element that has to be shifted to its correct position.
- The inner for loop, say j, starts from the last element of the sorted part i.e. i -1, and goes till the first element.
- If the element at i th index < element at j th index, we swap. Else break the loop.
Here is the code to implement iterative insertion sort in Java:
import java.util.*; public class InsertionSort { public static void main(String[] args) { int [] arr = {20, 10, 90, 4}; insertionSort(arr); System.out.println("Sorted Array is ->"); for(int var:arr) { System.out.print(var + " "); } } public static int [] insertionSort(int [] arr) { // outer loop keeping a track of no. of journeys for (int i = 1; i < arr.length; i++) { System.out.println("Journey "+ i); // maximum no. of passes for each element for(int j = i-1;j >= 0; j--) { // to define the pass number int pass = i-j; System.out.println("Pass "+ pass); System.out.println("Comparing " + arr[i]+ " and "+arr[j]); // if element is not at its correct position if(arr[j] > arr[j+1]) { swap(arr, j, j+1); }else { // the element is already at its correct position break; } } System.out.println(); } return arr; } public static void swap(int [] arr, int i ,int j) { System.out.println("Swapping " + arr[i]+ " and "+arr[j]); int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
Output:
Journey 1 Pass 1 Comparing 10 and 20 Swapping 20 and 10 Journey 2 Pass 1 Comparing 90 and 20 Journey 3 Pass 1 Comparing 4 and 90 Swapping 90 and 4 Pass 2 Comparing 90 and 20 Swapping 20 and 4 Pass 3 Comparing 90 and 10 Swapping 10 and 4 Sorted Array is -> 4 10 20 90
Now, to arrange the array in descending order we only change the condition of comparing the elements for swapping. If the element at j is less than the element at j+1 swapping occurs. Here is the Java code to implement iterative insertion sort in descending order:
import java.util.*; public class InsertionSort { public static void main(String[] args) { int [] arr = {20, 10, 90, 40, 30}; insertionSort(arr); System.out.println("Sorted Array is ->"); for(int var:arr) { System.out.print(var + " "); } } public static int [] insertionSort(int [] arr) { // outer loop keeping a track of no. of journeys for (int i = 1; i < arr.length; i++) { System.out.println("Journey "+ i); // maximum no. of passes for each element for(int j = i-1;j >= 0; j--) { // to define the pass number int pass = i-j; System.out.println("Pass "+ pass); System.out.println("Comparing " + arr[i]+ " and "+arr[j]); // if element is not at its correct position if(arr[j] < arr[j+1]) { swap(arr, j, j+1); }else { // the element is already at its correct position break; } } System.out.println(); } return arr; } public static void swap(int [] arr, int i ,int j) { System.out.println("Swapping " + arr[i]+ " and "+arr[j]); int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
Output:
Journey 1 Pass 1 Comparing 10 and 20 Journey 2 Pass 1 Comparing 90 and 10 Swapping 10 and 90 Pass 2 Comparing 10 and 20 Swapping 20 and 90 Journey 3 Pass 1 Comparing 40 and 10 Swapping 10 and 40 Pass 2 Comparing 10 and 20 Swapping 20 and 40 Pass 3 Comparing 10 and 90 Journey 4 Pass 1 Comparing 30 and 10 Swapping 10 and 30 Pass 2 Comparing 10 and 20 Swapping 20 and 30 Pass 3 Comparing 10 and 40 Sorted Array is -> 90 40 30 20 10
Time and Space Complexity
- Worst Case Scenario: When the whole array is in reverse order, to sort the array or for iteration of N-1, the total no. of passes goes like 1 + 2+ 3, and so on. This forms an arithmetic progression that sums up to n(n+1)/2. Therefore the time complexity is O( N^2).
- Best Case Scenario: When the complete array is sorted already, for the iteration of N-1, the no. of passes comes out to be 1 + 1+ 1 ---- N times. This Sums to N. Therefore time complexity is O(N).
- Average Case scenario: When the array elements are in random order, it still takes O(N^2) time complexity.
As no extra space is being used, the space complexity is O(1).
Recursive Insertion Sort Algorithm in Java
Now, we will discuss the algorithm for insertion sort with the recursive approach in ascending order:
- We create a function called recursiveInsertionSort() that takes up the array and the index value of the element that is to be placed at its correct position or the value of i.
- We implement the for loop of journeys recursively. The inner for loop remains as it is.
- As we are assuming the element at the 0th index to be sorted, we pass the index value or i as 1.
- We call the function recursiveInsertionSort() by incrementing the value of i by 1 till i = arr.length.
Here is the code to implement recursive insertion sort in Java:
import java.util.*; public class InsertionSort { public static void main(String[] args) { int [] arr = {20, 10, 90, 40,30}; recursiveinsertionSort(arr, 1); System.out.println("Sorted Array is ->"); for(int var:arr) { System.out.print(var + " "); } } public static void recursiveinsertionSort(int[] arr, int i) { // if i becomes equal to array's length, this implies all elements have been placed at their correct position if(i == arr.length) { return; } System.out.println("Journey "+ i); for(int j = i - 1; j >= 0; j--) { int pass = i-j; System.out.println("Pass "+ pass); System.out.println("Comparing " + arr[i]+ " and "+arr[j]); // if element is not at its correct position if(arr[j] > arr[j+1]) { swap(arr, j, j+1); }else { // the element is already at its correct position break; } } System.out.println(); recursiveinsertionSort(arr, i + 1); } public static void swap(int [] arr, int i ,int j) { System.out.println("Swapping " + arr[i]+ " and "+arr[j]); int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
Output:
Journey 1 Pass 1 Comparing 10 and 20 Swapping 20 and 10 Journey 2 Pass 1 Comparing 90 and 20 Journey 3 Pass 1 Comparing 40 and 90 Swapping 90 and 40 Pass 2 Comparing 90 and 20 Journey 4 Pass 1 Comparing 30 and 90 Swapping 90 and 30 Pass 2 Comparing 90 and 40 Swapping 40 and 30 Pass 3 Comparing 90 and 20 Sorted Array is 10 20 30 40 90
Is the Insertion Sort in place and stable?
A stable sorting technique is one in which the relative order of elements is maintained. As swapping takes place in insertion sort, no relative order of elements is changed, hence it is a stable sorting algorithm.
An in-place algorithm is one in which the changes happen in the input array only and no additional memory is used except for the input array. As insertion sort uses no extra space, it is an in-place algorithm.
Advantages & Applications
Insertion sort is best used when a small no. of elements are there in an array or only a few elements are left to be sorted in the array. It is mostly used in computer applications that construct complex programs like data compression or path-finding.
It is an online sorting algorithm, which means it can sort a list as it receives elements one by one. This can be useful in scenarios where new data continuously arrives and needs to be sorted incrementally. Also in situations like when given an array that is nearly sorted, insertion sort performs exceptionally well in such cases.
However, it becomes inefficient when the items in the input sequence are greater than 100 as it takes too much of time.
Conclusion
Despite having a time complexity of O( N^2), the algorithm sorts in place and takes no extra space as seen in the case of merge sort. Both bubble sort and insertion sort have the same time complexity but still insertion is better as it doesn't execute too many swaps as in bubble sort. Insertion sort in Java follows an incremental approach and sorts the array in an efficient way.








