When a large amount of data is to be dealt with, the most efficient way is to store it in an optimized manner, where it is arranged in either ascending or descending format. There are many sorting techniques like Merge Sort, Quick Sort, Bubble Sort, etc. In this article, we will study the Bubble Sort Algorithm, and understand how it works, with its implementation in C++.
What is Bubble Sort?
The Bubble Sort, also called Sinking Sort, is a sorting algorithm that compares each pair of adjacent elements. The basic technique of bubble sort is that the first element of the list is compared to the second, the second to the third element, and so on. Each iteration moves each element of the array closer to the end, similar to how air bubbles rise to the surface of the water.
This is how bubble sort gets its name. Here, the sorting is done in the form of passes or iterations. As a result, the largest element is placed in its rightful place in the list at the end of each iteration.
If you are new to programming this might be the first sorting technique you will learn because it is easy to understand, and simple to code. Sorting is one of the most basic concepts that programmers need to learn and Bubble Sort is your entry point in this new world. You can store and optimize a huge amount of data when you will work in the real world.
Algorithm of Bubble Sort
Here is the basic algorithm for Bubble Sort:
Step1: for k = 0 to n-1 repeat Step 2 Step2: for j = k + 1 to n – k repeat Step3: if A[j] > A[k] Swap A[j] and A[k] [end of inner for loop] [end if outer for loop] Step4: end
Optimized Bubble Sort
Although bubble sort is simple to understand and implement, it can be optimized to improve its efficiency. The optimization involves checking whether any swaps were made in each pass. If no swaps were made, it means that the array is already sorted, and the algorithm can terminate early.
To optimize bubble sort, we introduce an additional variable called swapped. This variable keeps track of whether any swaps were made in a pass. If no swaps were made, swapped remains false, and the algorithm terminates.
How Does Bubble Sort Work?
- If the order of adjacent elements is incorrect, we compare them ( a[k] > a[j] ) and swap them.
- Assume we have an array of length 'n'. Therefore, to sort 'n' elements using the previous step, we require an 'n-1' pass.
- After following these steps, the largest element goes to the end of the array. The next largest is one place behind the last. The 'kth' largest element is swapped to its rightful place in the array in the 'kth' pass.
- So basically, at least one element from 'n - k + 1' will appear at its right place at the end of the ith pass. It will be the 'kth' largest element (for 1 *= k *= n - 1) of the array. Because in the 'kth' pass of the array, in the 'jth' iteration (for 1 <= j <= n - k), we are checking if 'a[j] > a[j + 1]', and 'a[j]' will always be greater than 'a[j + 1]' when it is the largest element in range '[1, n - k + 1]'. We'll now swap it.
- The process will continue until the largest element in the array is at the '(n - k + 1)th' position.
Following is the pseudocode of Bubble Sort Algorithm:
begin bubbleSort(array): N <- length(array) for j = 0 to N: for i = 0 to N-1: if array[i] > array[i+1] temp <- array[i] array[i+1] <- array[i] array[i] <- temp end if end for end for return array
end bubbleSort
begin modifiedbubbleSort(array): N <- length(array) for j = 0 to N: flag = False for i = 0 to N-1: if array[i] > array[i+1] temp <- array[i] array[i+1] <- array[i] array[i] <- temp flag = True end if end for if flag == False: break end for return array end modifiedbubbleSort
Here, we traverse the array using two iterative loops.
We begin with the '0th' element in the first loop, then we begin with an adjacent element in the second loop. We compare each of the neighboring components in the inner loop body and swap them if they are out of order. The heaviest element bubbles up at the end of each iteration of the outer loop.
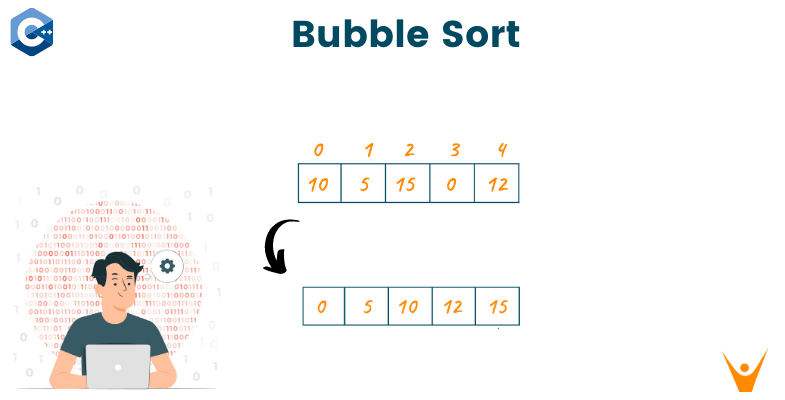
Bubble Sort Example
Let us consider the below array of elements to sort.
As we can see from the above illustration, the greatest element bubbles up to the last with each pass, sorting the list. Each element is compared to its adjacent element and switched with one another if they are not in order.
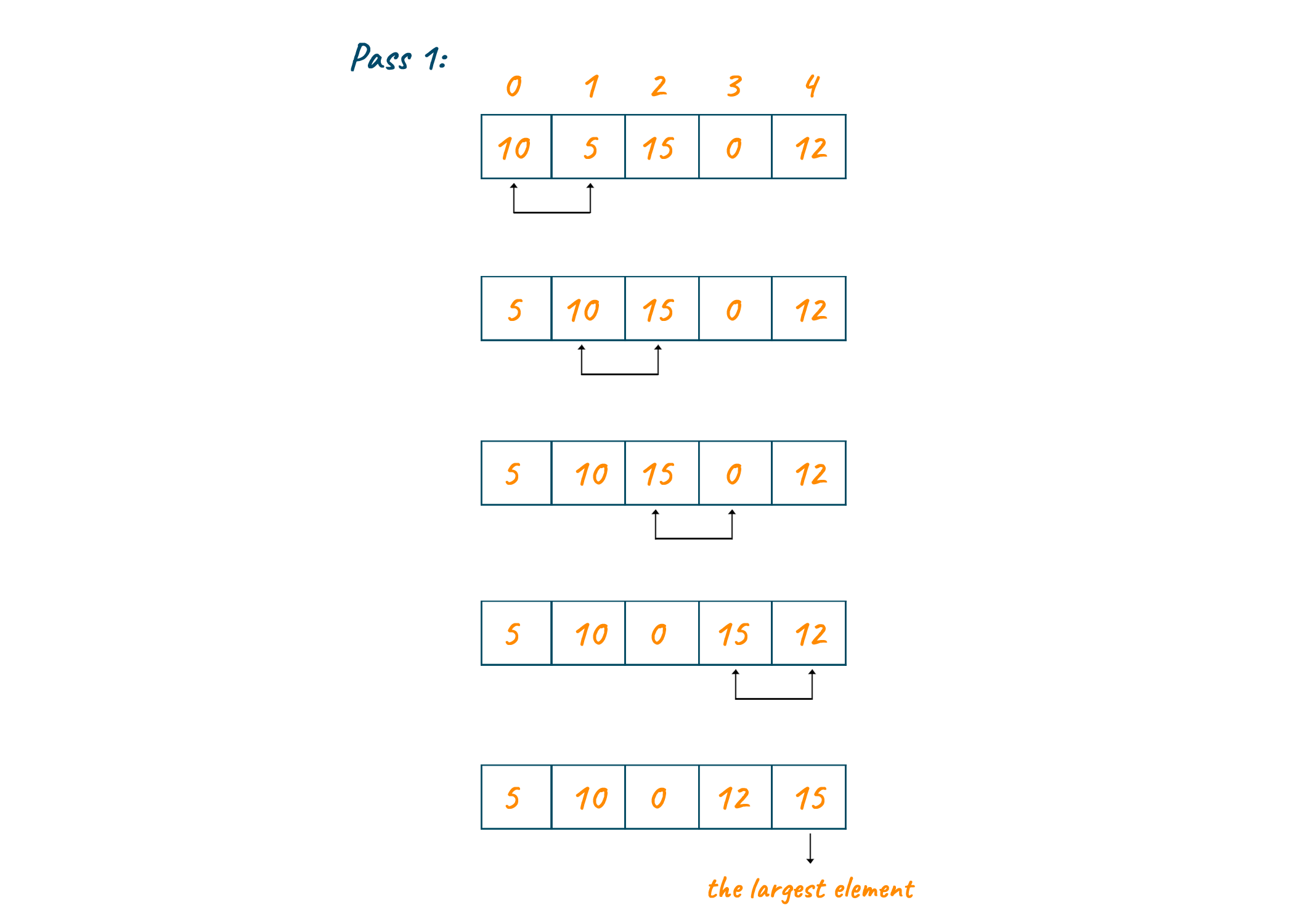
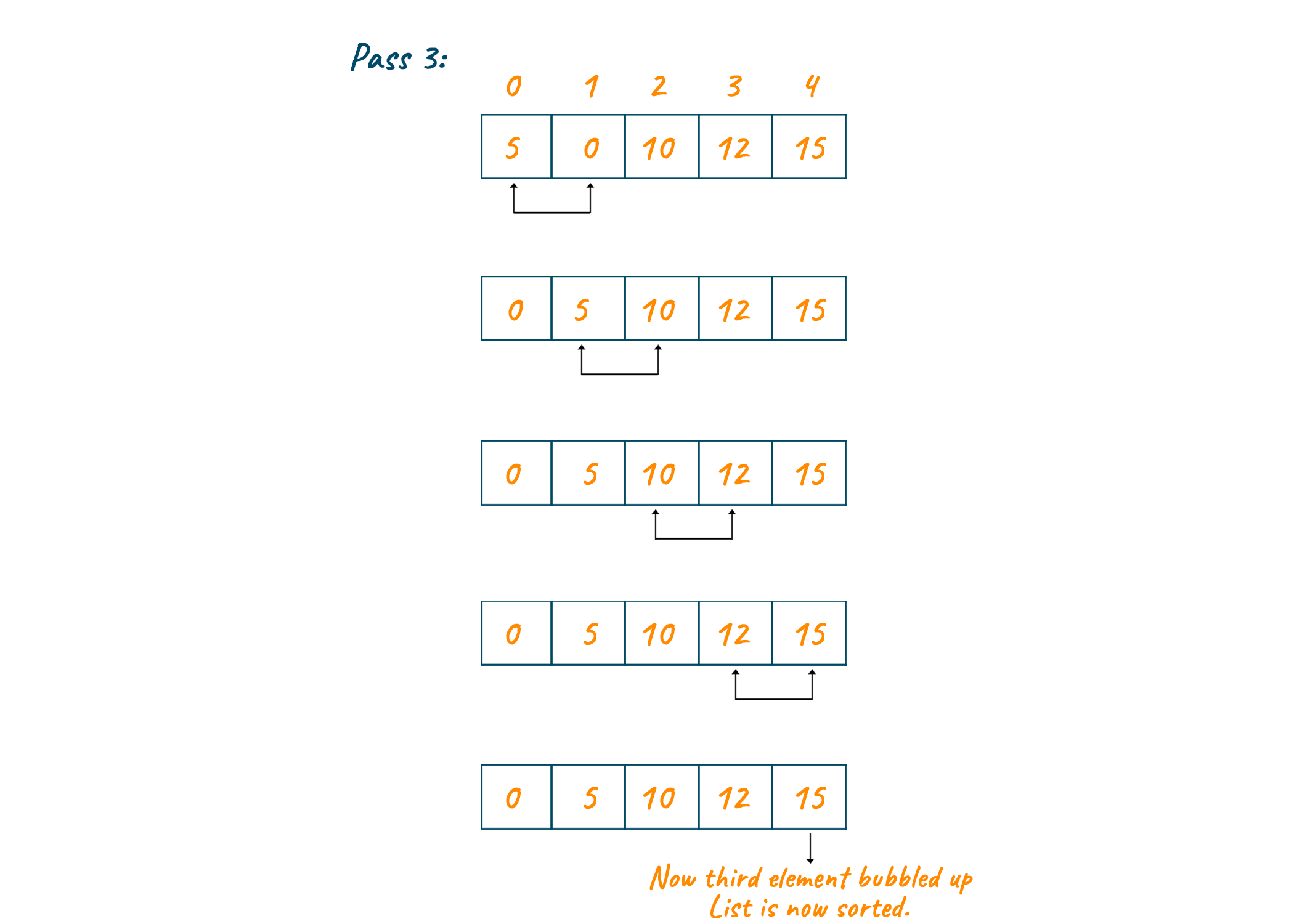
If the array is to be sorted in ascending order at the end of the first pass, the largest element is placed at the end of the list. The second largest element is placed at the second last position in the list for the second pass, and so on.

At last, we will have sorted the entire list when n-1 (where n is the total number of entries in the list) passes. The final output of the bubble sort will be as shown below.
C++ Program for Bubble Sort
Here is the C++ Program with complete code to implement Bubble Sort:
#include<bits/stdc++.h> #define swap(x,y) { x = x + y; y = x - y; x = x - y; } using namespace std; /** * Function to Sort the array using Modified Bubble Sort Algorithm * @param arr: Array to be Sorted * @param n: Size of array * @return : None */ void bubbleSort(int arr[], int n) { int i, j; bool flag; // Outer pass for(i = 0; i < n; i++) { flag = false; // Set flag as false for(j = 0; j < n-i-1; j++) { // Compare values if( arr[j] > arr[j+1]) { swap(arr[j],arr[j+1]); flag = true; } } // If no to elements are swapped then // array is sorted. Hence Break the loop. if(!flag) { break; } } } int main(int argv, char* argc[]) { int arr[] = {1,5,6,8,3,4,7,2,9}; int n = sizeof(arr)/sizeof(int); cout<<"Unsorted Array :"; for(int i=0;i<n;i++) // Print the Original Array cout<<arr[i]<<" "; cout<<endl; bubbleSort(arr,n); // Call for Bubble Sort Function cout<<"Sorted Array :"; for(int i=0;i<n;i++) // Print the Sorted Array cout<<arr[i]<<" "; return(0); }
Output:
Unsorted Array :1 5 6 8 3 4 7 2 9 Sorted Array :1 2 3 4 5 6 7 8 9
Time Complexity
The time complexity of bubble sort can be analyzed by considering the number of comparisons and swaps performed during the sorting process.
Best Case
The best case occurs when the array is already sorted. In this case, bubble sort still performs the comparisons but does not need to perform any swaps. The time complexity in the best case is O(n).
Average Case
The average case occurs when the array is in random order. In this case, bubble sort performs both comparisons and swaps. The time complexity in the average case is O(n^2).
Worst Case
The worst case occurs when the array is sorted in reverse order. In this case, bubble sort performs the maximum number of comparisons and swaps. The time complexity in the worst case is O(n^2).
Space Complexity
The space complexity of bubble sort is O(1) because it only requires a few extra variables to perform the sorting and does not require any additional memory proportional to the input size.
Recursive Implementation of Bubble Sort
A recursive version of Bubble sort is a variant of the Bubble sort algorithm that sorts an array using recursion. In recursive bubble sort, the first n-1 elements of the array are sorted, and then the remaining n-1 elements of the array are sorted recursively. When we reach an array of size one, the recursion ends.
We have given below the example code for recursive implementation:
// Recursive Bubble Sort function void bubbleSortRecursive(int arr[], int n) { // Base case if (n == 1) return;
for (int i=0; i<n-1; i++) if (arr[i] > arr[i+1]) swap(arr[i], arr[i+1]); // Recursively sort the remaining n-1 elements bubbleSortRecursive(arr, n-1); }
Is the Bubble Sort algorithm stable?
A sorting algorithm is said to be stable when the relative order of equal elements in the sorted output remains the same as it did in the original input. This means that if two elements in the input array have the same value and appear in a given order, the algorithm will keep that order in the final output.
The bubble sort is a stable sorting algorithm because it guarantees that the relative order of equal components is maintained. Since it swaps neighboring elements only if they are out of order and not if they are equivalent, there is no change in order.
Why is Bubble Sort not efficient?
The main reason why Bubble sort is not considered efficient since it has a time complexity of O(n2), which implies that the time required to sort the input array grows quadratically as the size of the array grows. This makes sorting huge arrays impractical since it becomes progressively sluggish and resource intensive.
Furthermore, it requires several swaps between neighboring items, which can be expensive in terms of memory access, especially when the input data is stored in an external memory such as a hard disc or flash drive.
Advantages of Bubble Sort
Bubble sort has some advantages that make it useful in certain scenarios:
- Simplicity: Bubble sort is one of the simplest sorting algorithms to understand and implement. It is an excellent algorithm for beginners to learn about sorting techniques.
- In-place Sorting: Bubble sort operates on the original array, without requiring any additional memory. This makes it memory-efficient and useful in situations with limited memory resources.
- Stable Sorting: Bubble sort is a stable sorting algorithm, meaning that elements with equal values maintain their relative order in the sorted array. This property is crucial in certain applications where the order of equal elements matters.
Disadvantages of Bubble Sort
Despite its simplicity, bubble sort also has some disadvantages:
- Inefficiency: Bubble sort has a time complexity of O(n^2), which makes it highly inefficient for large data sets. It performs a large number of unnecessary comparisons and swaps, leading to slow performance.
- Lack of Adaptability: Bubble sort does not adapt to the input data's initial order. It performs the same number of iterations and comparisons regardless of whether the array is already sorted or partially sorted.
- Not Suitable for Complex Data Structures: Bubble sort is not suitable for sorting complex data structures such as linked lists or trees, where accessing elements requires more than simple indexing.
Conclusion
We studied Bubble Sort in this blog with how it works and the C++ program to implement it. It is not commonly used compared to other sorting algorithms but still has its own importance in the technical world. Learning bubble sort is well worth the effort because it acts as a bridge to understanding higher-level concepts and makes it easier.