Used in database systems, AVL Trees are very important to learn for a Python programmer. In this article, we will study all about AVL Tree in Python and why we should use it. We will learn the rotation operations, along with the insertion and deletion operations with code. So, let's get started!
What Is an AVL Tree?
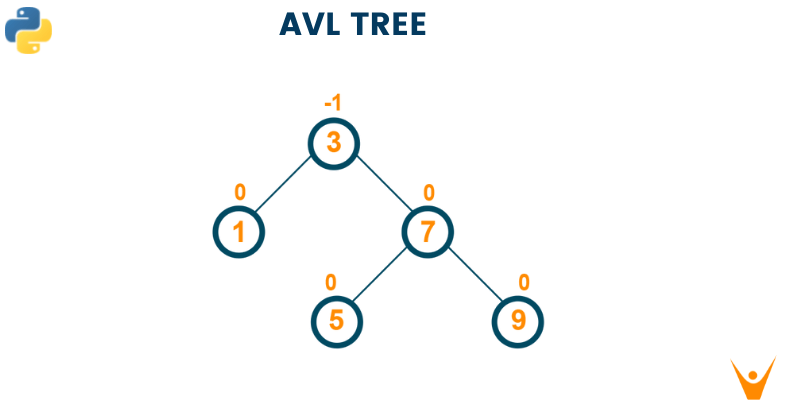
The full form of an AVL is Adelson-Velskii and Landis also known as a height binary tree. A tree is called an AVL tree if each node of the tree possesses one of the following properties:
- A node is called left heavy if the longest path in its left subtree is one longer than the longest path of its right subtree
- A node is called right heavy if the longest path in the right subtree is one longer than the path in its left subtree
- A node is called balanced if the longest path in both the right and left subtree are equal.
AVL tree is a height-balanced tree where the difference between the heights of the right subtree and left subtree of every node is either -1, 0, or 1. The difference between the heights of the subtree is maintained by a factor named as balance factor. Therefore, we can define AVL as it is a balanced binary search tree where the balance factor of every node in the tree is either -1, 0, or +1.
Here, the balance factor is calculated by the formula:
Balance Factor = Height Of Left Subtree - Height Of Right Subtree
As AVL is the height-balanced tree, it helps to control the height of the binary search tree and further helps the tree to prevent skewing. When the binary tree gets skewed, the running time complexity becomes the worst-case scenario i.e. O(n) but in the case of the AVL tree, the time complexity remains O(logn). Therefore, it is always advisable to use an AVL tree rather than a binary search tree.
Remember that every AVL Tree is a binary search tree but every Binary Search Tree need not be AVL Tree.
AVL Rotation
When certain operations like insertion and deletion are performed on the AVL tree, the balance factor of the tree may get affected. If after the insertion or deletion of the element, the balance factor of any node is affected then this problem is overcome by using rotation.
Therefore, rotation is used to restore the balance of the search tree. Rotation is the method of moving the nodes of trees either to left or to right to make the tree heightened balance tree. There are total two categories of rotation which are further divided into two further parts:
1) Single Rotation
Single rotation switches the roles of the parent and child while maintaining the search order. We rotate the node and its child, the child becomes a parent.
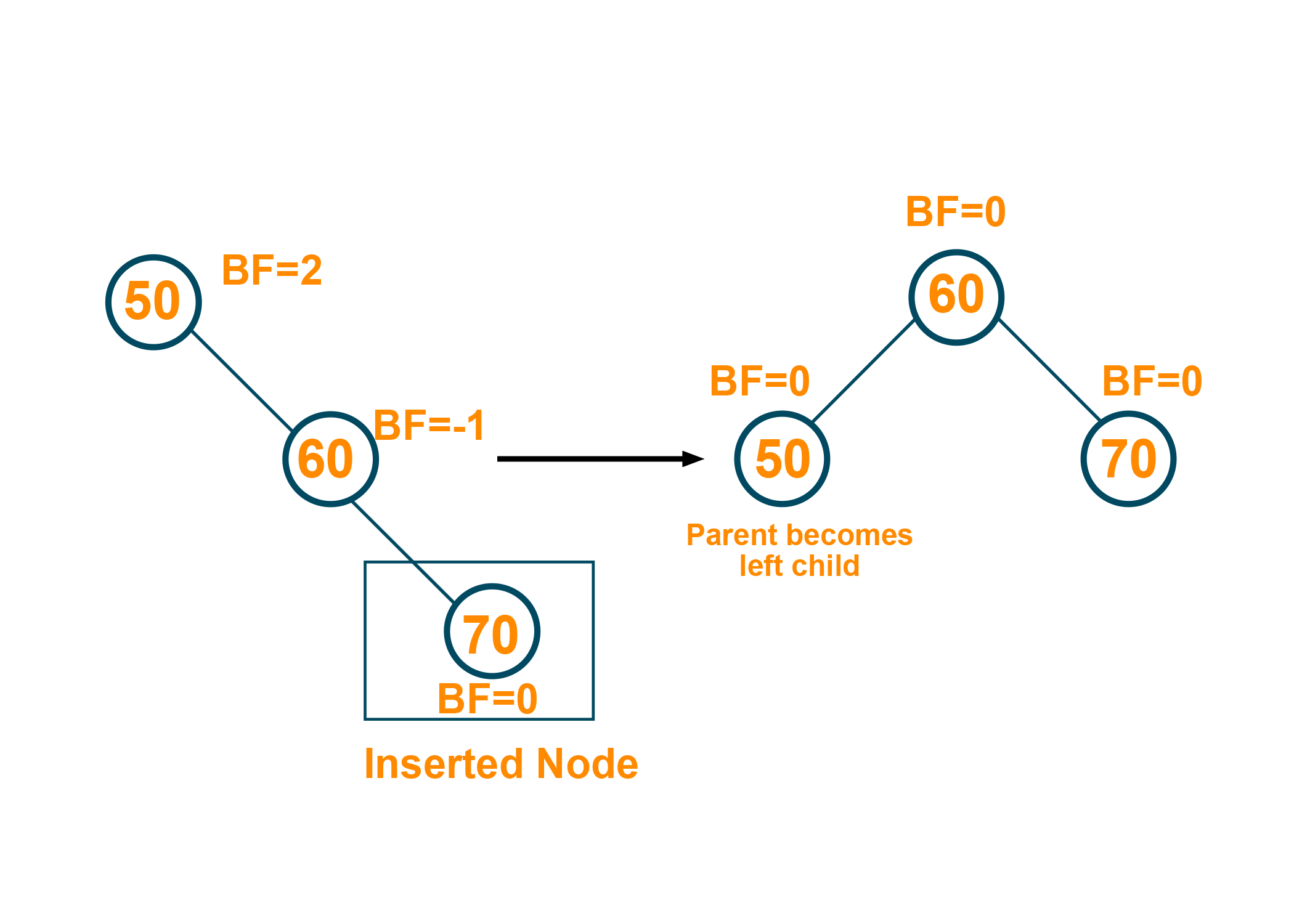
Single LL(Left Left) Rotation
Here, every node of the tree moves toward the left from its current position. Therefore, a parent becomes the right child in the LL rotation. Let us see the below examples:
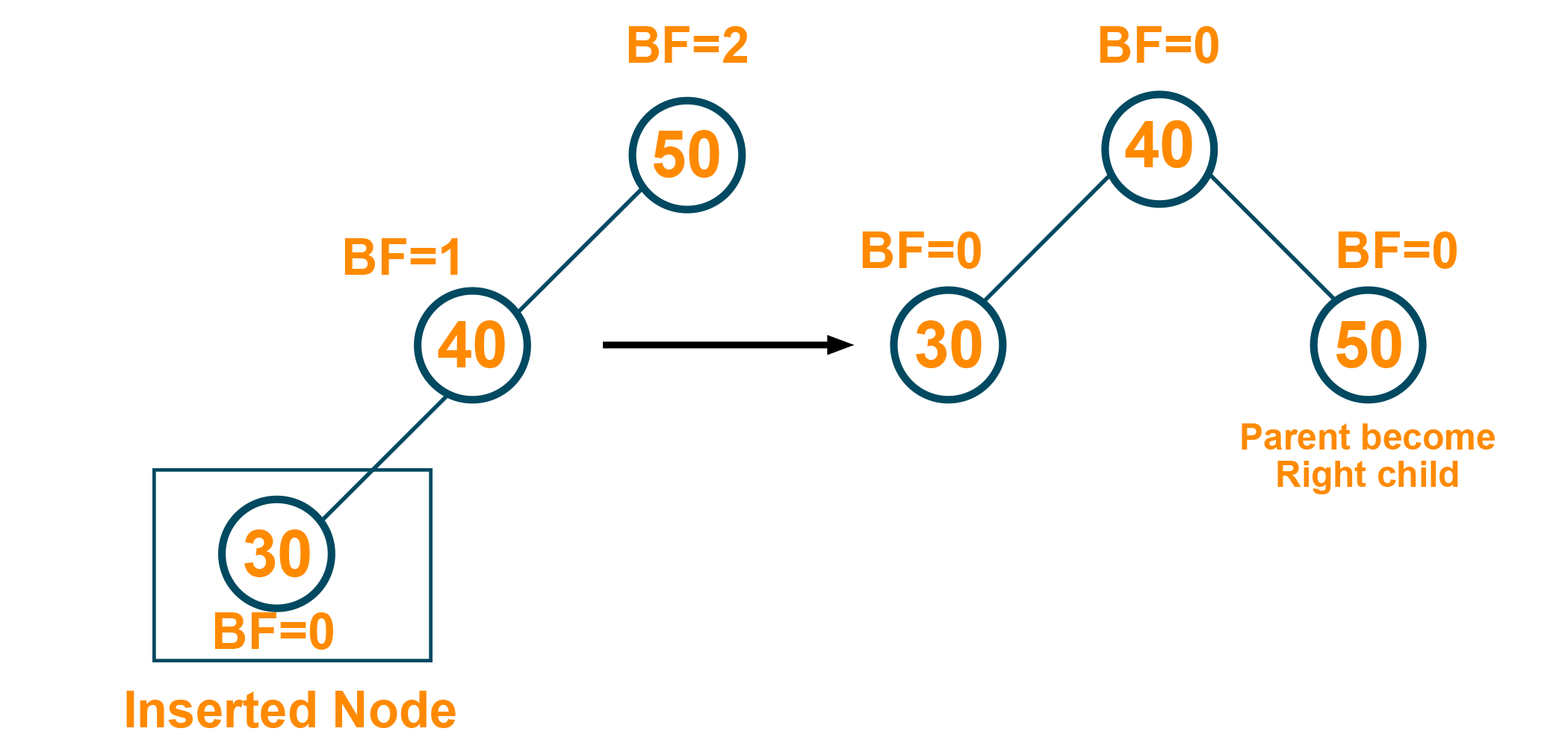
Single RR(Right Right) Rotation
Here, every node of the tree moves toward the right from the current position. Therefore, the parent becomes a left child in RR rotation. Let us see the below example:
2) Double Rotation
Single rotation does not fix the LR rotation and RL rotation. For this, we require double rotation involving three nodes. Therefore, double rotation is equivalent to the sequence of two single rotations.
LR(Left-Right) Rotation
The LR rotation is the process where we perform a single left rotation followed by a single right rotation. Therefore, first, every node moves towards the left and then the node of this new tree moves one position towards the right. Let us see the below example:

RL (Right-Left) Rotation
The RL rotation is the process where we perform a single right rotation followed by a single left rotation. Therefore, first, every node moves towards the right and then the node of this new tree moves one position towards the left. Let us see the below example:
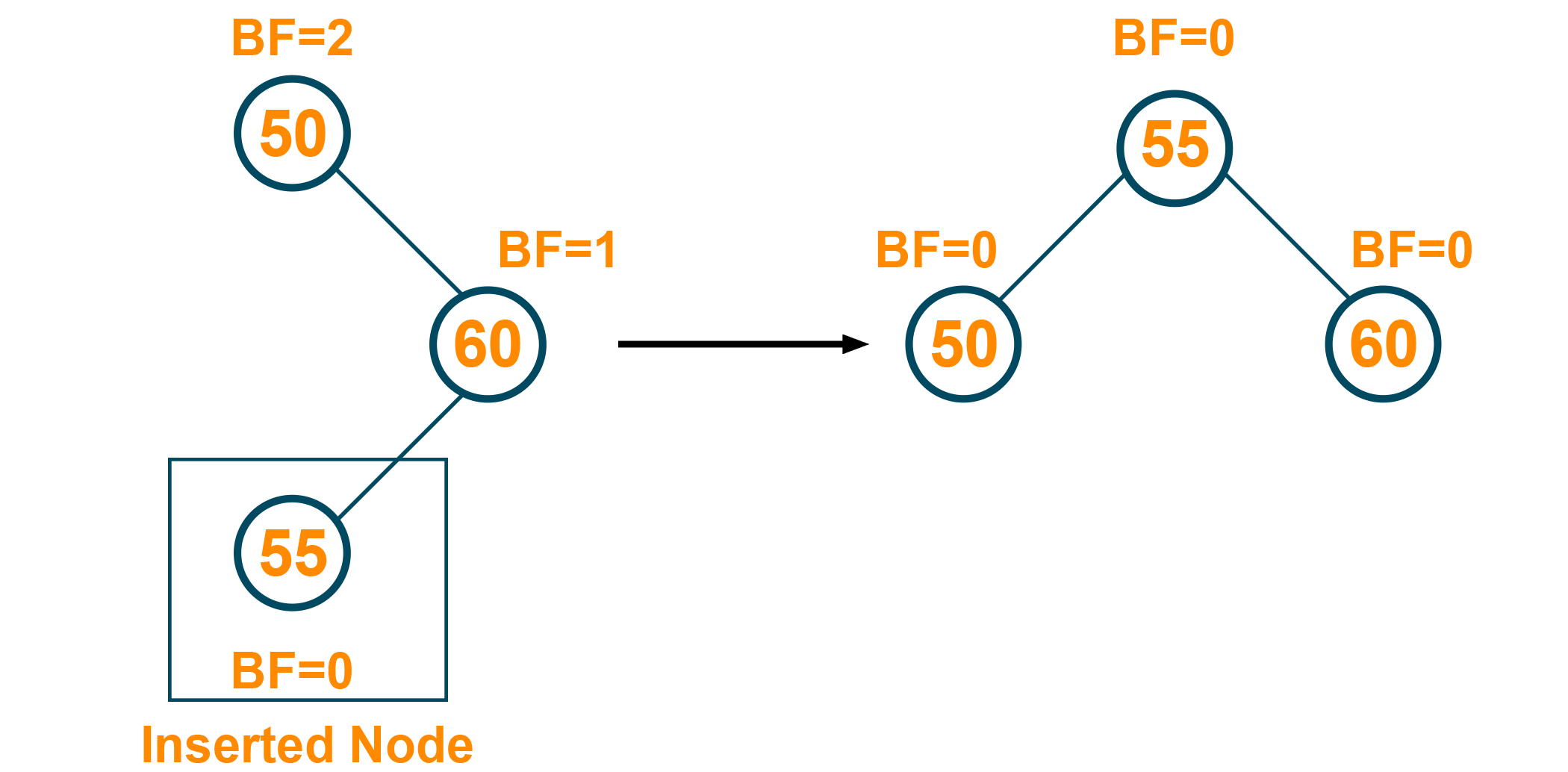
Insertion Operation In AVL Tree
In the AVL tree, the new node is always added as a leaf node. After the insertion of the new node, it is necessary to modify the balance factor of each node in the AVL tree using the rotation operations. The algorithm steps of insertion operation in an AVL tree are:
- Find the appropriate empty subtree where the new value should be added by comparing the values in the tree
- Create a new node at the empty subtree
- The new node is a leaf ad and thus will have a balance factor of zero
- Return to the parent node and adjust the balance factor of each node through the rotation process and continue it until we are back at the root. Remember that the modification of the balance factor must happen in a bottom-up fashion.
Example:
The root node is added as shown in the below figure:
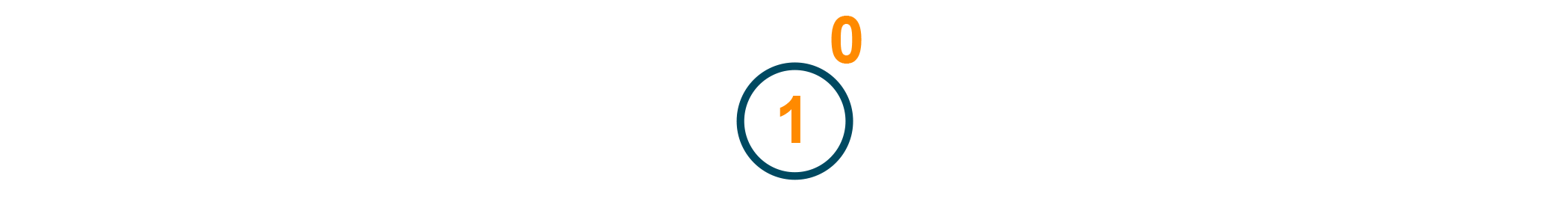
The node to the root node is added as shown below. Here the tree is balanced!
Then, The right child is added to the parent node. Here, the balance factor of the tree is changed, therefore, the LL rotation is performed and the tree becomes a balanced tree:

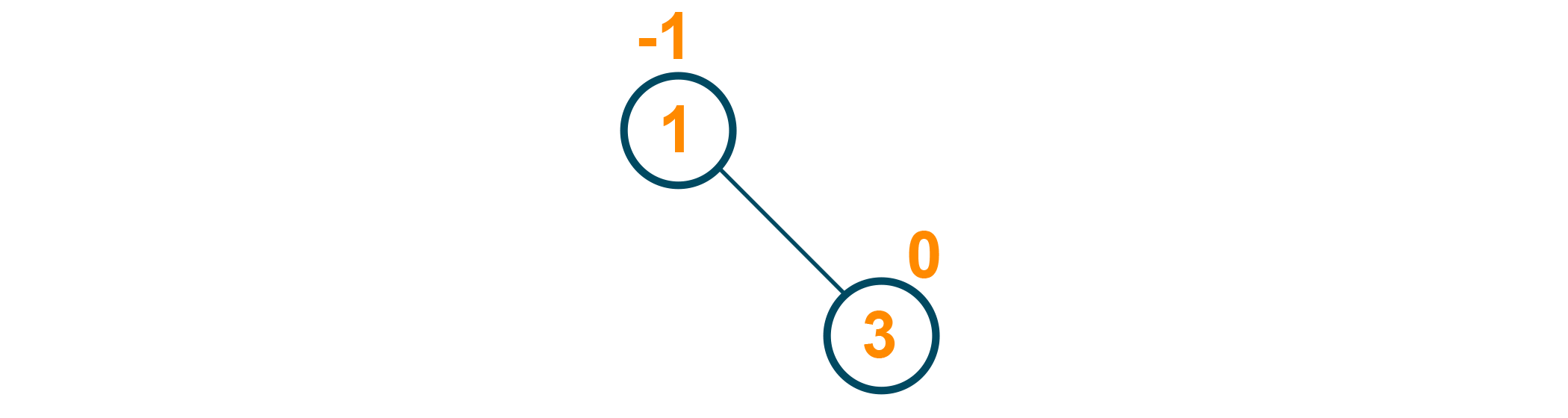
Later, one more right child is added to the new tree as shown below:
Again further, one more right child is added and the balance factor of the tree is changed. Therefore, again LL rotation is performed on the tree and the balance factor of the tree is restored as shown in the below figure
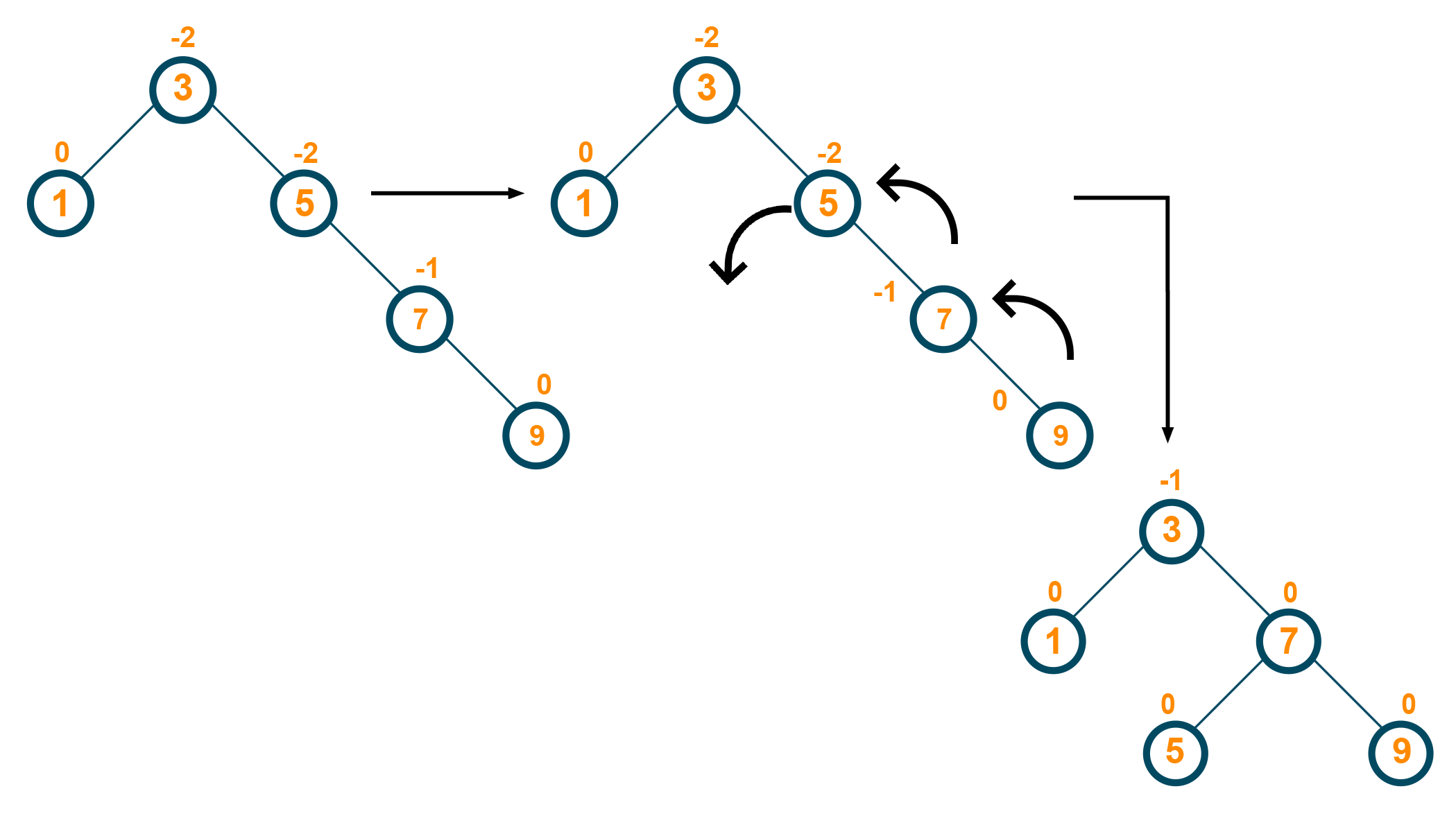
Deletion Operation In AVL
The deletion operation in the AVL tree is the same as the deletion operation in BST. In the AVL tree, the node is always deleted as a leaf node and after the deletion of the node, the balance factor of each node is modified accordingly. Rotation operations are used to modify the balance factor of each node. The algorithm steps of deletion operation in an AVL tree are:
- Locate the node to be deleted
- If the node does not have any child, then remove the node
- If the node has one child node, replace the content of the deletion node with the child node and remove the node
- If the node has two children nodes, find the inorder successor node ‘k' which has no child node and replace the contents of the deletion node with the ‘k’ followed by removing the node.
- Update the balance factor of the AVL tree
Example:
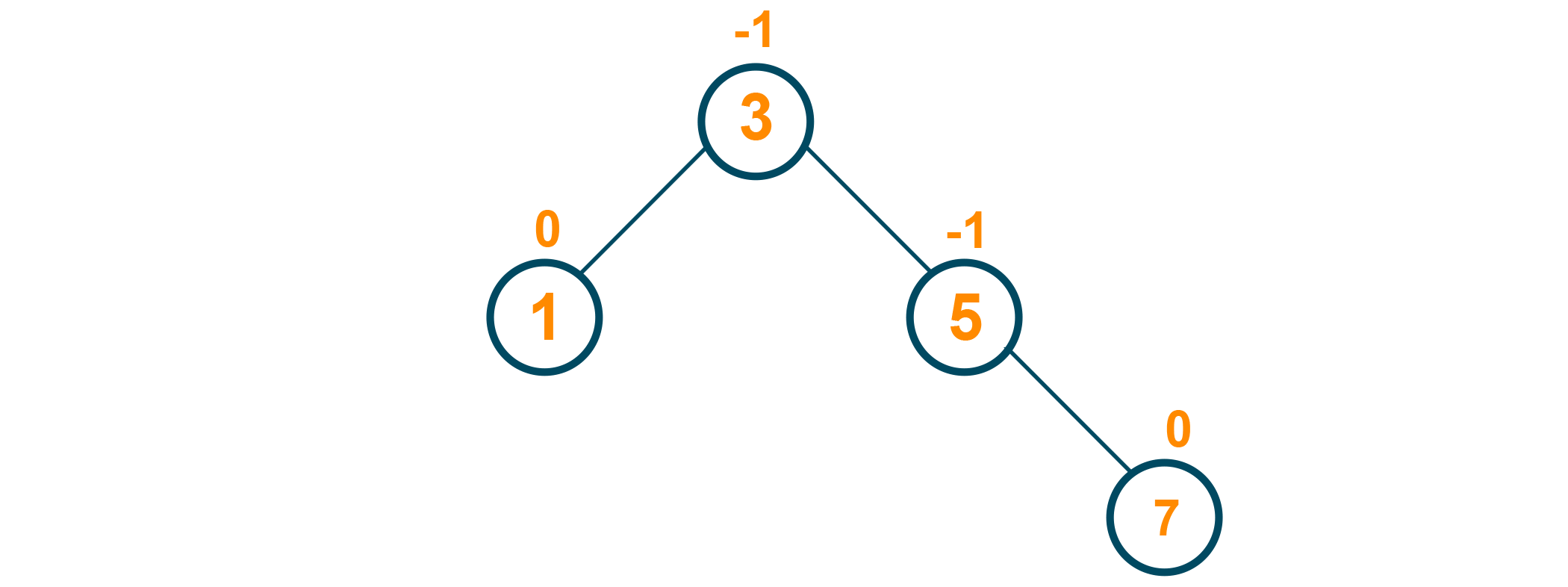
Let us consider the below AVL tree with the given balance factor as shown in the figure below:
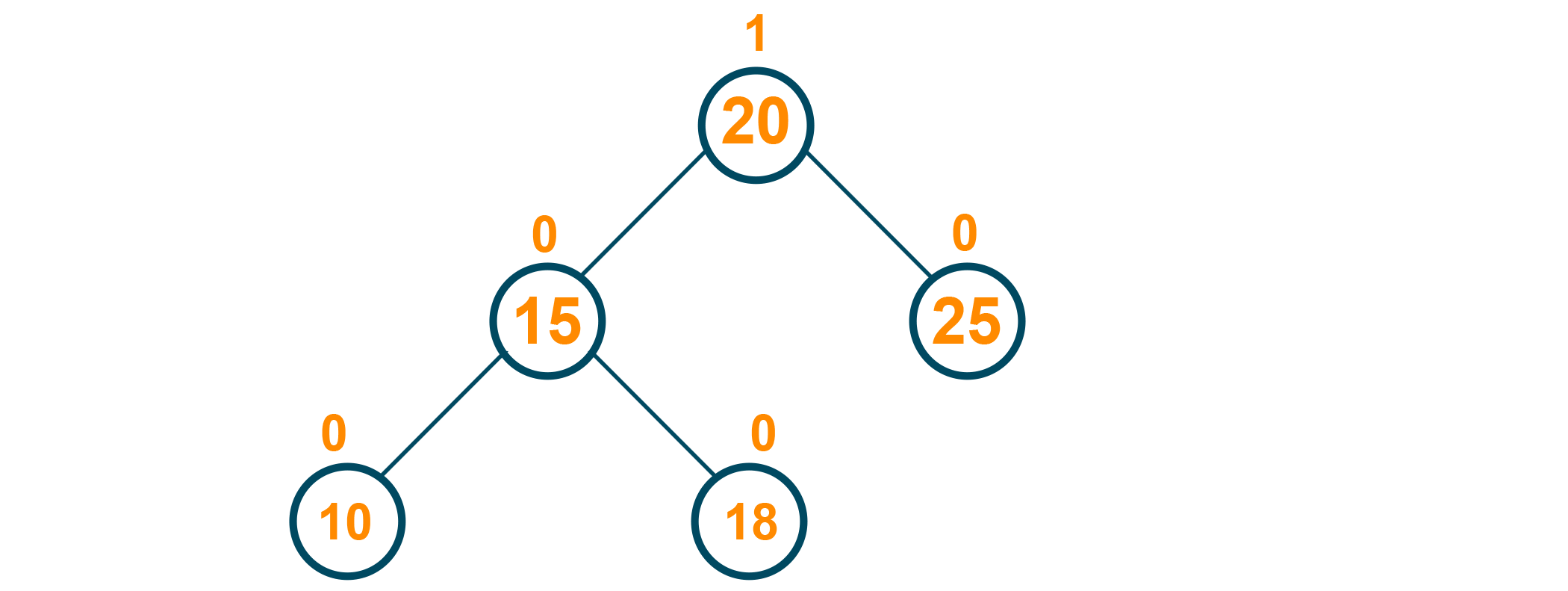
Here, we have to delete the node '25' from the tree. As the node to be deleted does not have any child node, we will simply remove the node from the tree:

After removal of the tree, the balance factor of the tree is changed and therefore, the rotation is performed to restore the balance factor of the tree and create a perfectly balanced tree:
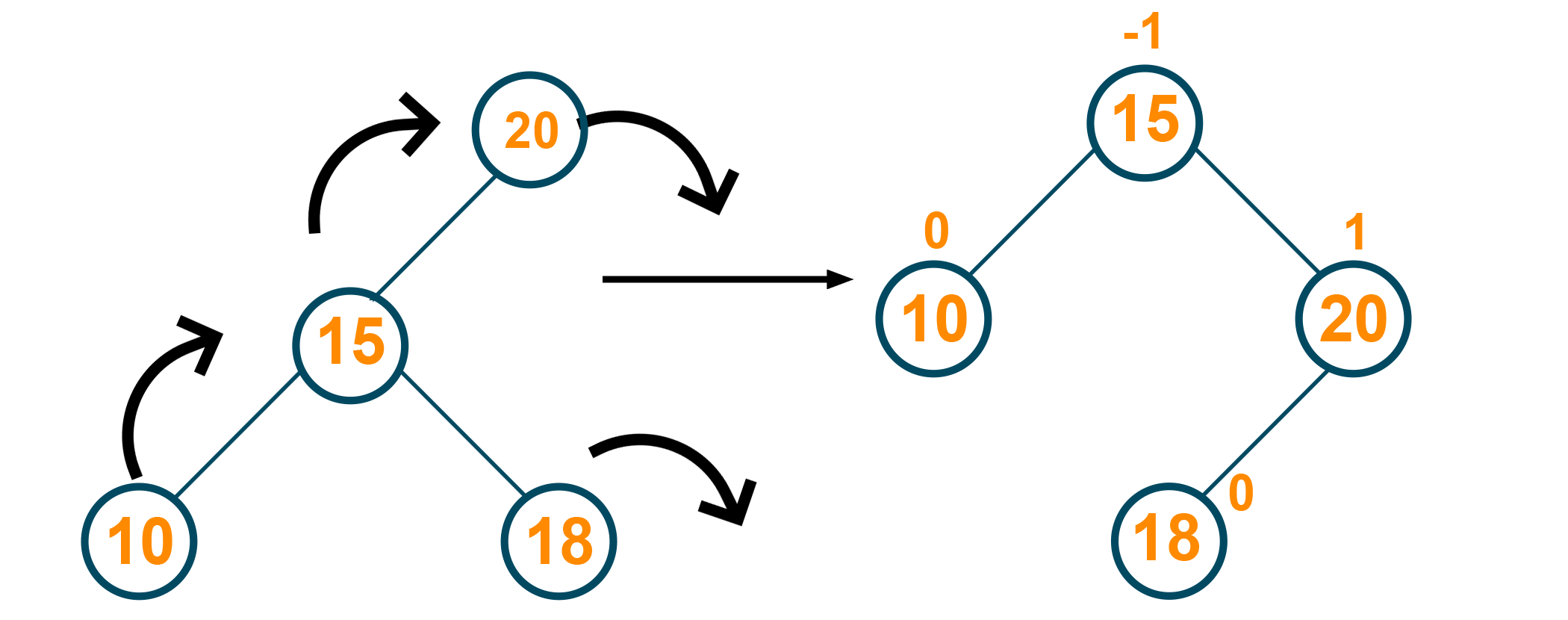
Does Python have an AVL tree?
Python's standard library does not include an AVL tree implementation. There are, however, a number of third-party libraries available that provide AVL tree functionality.
The 'avl tree' is a popular Python library for working with AVL trees, and it can be installed with pip: pip install avl_tree.
Here's an example of how to use the avl_tree library to create an AVL tree.
from avl_tree import AVLTree tree = AVLTree()?
tree.insert(1) tree.insert(3) tree.insert(9) tree.insert(2) tree.insert(1) tree.insert(6) tree.insert(5)
Balance Factor of AVL Tree in Python
The balance factor of an AVL tree is a measure of the tree's balance. It is defined as the difference in heights between a node's left and right subtrees. For an AVL tree to remain balanced, the balance factor of any node must be -1, 0, or 1.
If the balance factor is anything else, the tree needs to be rebalanced. Then, we need to rebalance an AVL tree and perform one or more rotations on the tree to restore the balance factor of each node.
Python Code For AVL Tree
Below is the complete code to implement AVL Tree in Python:
class treeNode(object): def __init__(self, value): self.value = value self.l = None self.r = None self.h = 1 class AVLTree(object): def insert(self, root, key): if not root: return treeNode(key) elif key < root.value: root.l = self.insert(root.l, key) else: root.r = self.insert(root.r, key) root.h = 1 + max(self.getHeight(root.l), self.getHeight(root.r)) b = self.getBal(root) if b > 1 and key < root.l.value: return self.rRotate(root) if b < -1 and key > root.r.value: return self.lRotate(root) if b > 1 and key > root.l.value: root.l = self.lRotate(root.l) return self.rRotate(root) if b < -1 and key < root.r.value: root.r = self.rRotate(root.r) return self.lRotate(root) return root def lRotate(self, z): y = z.r T2 = y.l y.l = z z.r = T2 z.h = 1 + max(self.getHeight(z.l), self.getHeight(z.r)) y.h = 1 + max(self.getHeight(y.l), self.getHeight(y.r)) return y def rRotate(self, z): y = z.l T3 = y.r y.r = z z.l = T3 z.h = 1 + max(self.getHeight(z.l), self.getHeight(z.r)) y.h = 1 + max(self.getHeight(y.l), self.getHeight(y.r)) return y def getHeight(self, root): if not root: return 0 return root.h def getBal(self, root): if not root: return 0 return self.getHeight(root.l) - self.getHeight(root.r) def preOrder(self, root): if not root: return print("{0} ".format(root.value), end="") self.preOrder(root.l) self.preOrder(root.r) Tree = AVLTree() root = None root = Tree.insert(root, 1) root = Tree.insert(root, 2) root = Tree.insert(root, 3) root = Tree.insert(root, 4) root = Tree.insert(root, 5) root = Tree.insert(root, 6) # Preorder Traversal print("Preorder traversal of the", "constructed AVL tree is") Tree.preOrder(root) print()
Output:
4 2 1 3 5 6
Search in AVL tree with Python
To search for a value in an AVL tree, you can use the search method provided by the AVL tree library. We will consider the same tree as mentioned in the previous example. Here is the code:
from avl_tree import AVLTree tree = AVLTree()?
tree.insert(1) tree.insert(3) tree.insert(9) tree.insert(2) tree.insert(1) tree.insert(6) tree.insert(5) # search for a value in the tree result = tree.search(4) if result is not None: print("Value found:", result) else: print("Value not found”)
We create an AVLTree object using the avl_tree library and then insert some values into the tree using the insert method. We then search for the value 4 using the search method and print out the result.
Output:
value not found
AVL Tree Time Complexity
For insertion operation, the running time complexity of the AVL tree is O(log n) for searching the position of insertion and getting back to the root.
Similarly, the running time complexity of the deletion operation of the AVL tree is also O(log n) for finding the node to be deleted and performing the operations later to modify the balance factor of the AVL tree. The time complexity of the AVL tree is faster and constant in comparison to the binary search tree.
Advantages & Disadvantages of AVL
AVL tree is a height-balanced tree and therefore, the height of the tree never grows more than N where N is the number of nodes in the tree. It has efficient search time complexity. Also, it is faster than the Red-Black tree in Python as the AVL tree is more strictly balanced.
But they are also very very difficult to implement and the constant factors for operations are very high.
Applications of AVL Tree
Following are some of its popular use cases:
- AVL tree is used when there are few operations of insertion and deletion are performed
- It is used when a short search time is needed.
- It is effective to search the data fast and efficiently in large databases.
- It is widely used for sorting sets and dictionary data.
- It is used in applications where the searching should be effective rather than in database applications.
Conclusion
We learned everything about AVL Tree in Python with code. It is used for faster and more efficient searching of data in a large dataset and therefore, it is always recommended to learn and understand it in detail. Happy Learning :)