In this article, we will study what is a red-black tree is and why it is useful. We will understand various operations of the red-black tree along with their algorithm, example, and python code. Later we will also go through various advantages, disadvantages, and applications of the red-black tree.
What is a Red-Black Tree?
A red-black tree is the variation of the binary search tree with the property of self-balancing. A red-black tree is also called symmetric binary B-Tree. Every node of the red-black tree contains an extra attribute denoting the color of the node, specifically, either red or black. The importance of these colors in the nodes of the tree ensures that the tree is balanced while insertion and deletion operations of the node. Therefore, the red-black tree follows the below properties:
- Tree Property: Red-Black tree should be a binary search tree.
- Red/Black Property: Every node of the tree is colored either red or black.
- Root Property: The color attribute of the root node is always black.
- Leaf Property: Every leaf of the tree is black.
- Red Property: The child node is always black if the parent node is red in color. Therefore, there should not be two consecutive red nodes.
- Depth Property: Every path from the root node to any leaf node should have the same number of black-colored nodes.
Remember that every node of the red-black tree consumes only 1 bit of memory storage to store the color information, hence the tree is identical to the classic binary search tree.
Why Use Red-Black Tree?
As you know that binary search tree maintains the natural order of the data inserted, but it does not restrict the size, length, or height of the tree. Consider the below image where the nodes inserted in the binary search tree are 10,20,30,40,50. Here, the height of the tree is 5 as the tree grows linearly when the new node is inserted. Hence, as the height of the tree grows linearly, the search operation in the tree becomes the worst-case scenario and takes O(n) time where n is the total number of nodes inserted.

This problem can be solved by using a red-black tree. As the red-black tree maintains its height of the tree after every insertion and deletion operation, the tree can be avoided from skewing. Therefore, the time complexity for search operation is reduced to O(log n) where n is the number of nodes in the tree.
Instead of a red-black tree, you can also use an AVL tree to balance the height of the tree. But it is noted, that the red-black tree makes fewer structural changes to balance the height of the tree in comparison to AVL trees. Hence, the red-black tree is potentially faster during insertion and deletion operations in comparison to AVL trees.
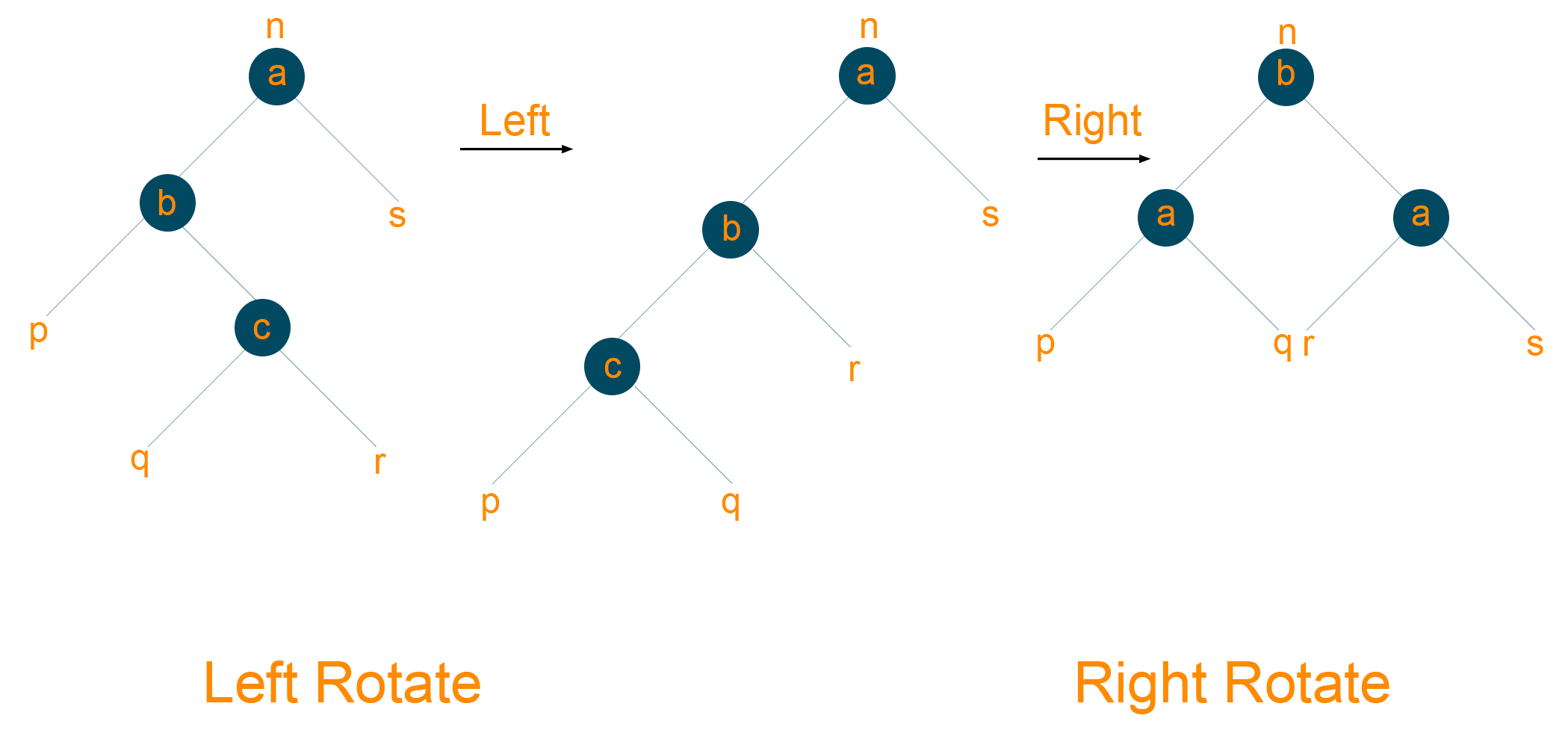
Rotations in Red Black Tree
The rotation is the process of adjusting or interchange the nodes of the subtrees inside the tree in such a way that the height of the tree is restored. It helps to maintain the red-black tree properties which are sometimes violated while insertion and deletion operations. Basically, there are two types of rotation in Red-Black Tree:
1) Left Rotation
The nodes on the right of the tree are transformed on the left node is called the left rotation. Look at the below algorithm for understanding.
Algorithm
- Consider the below red-black tree
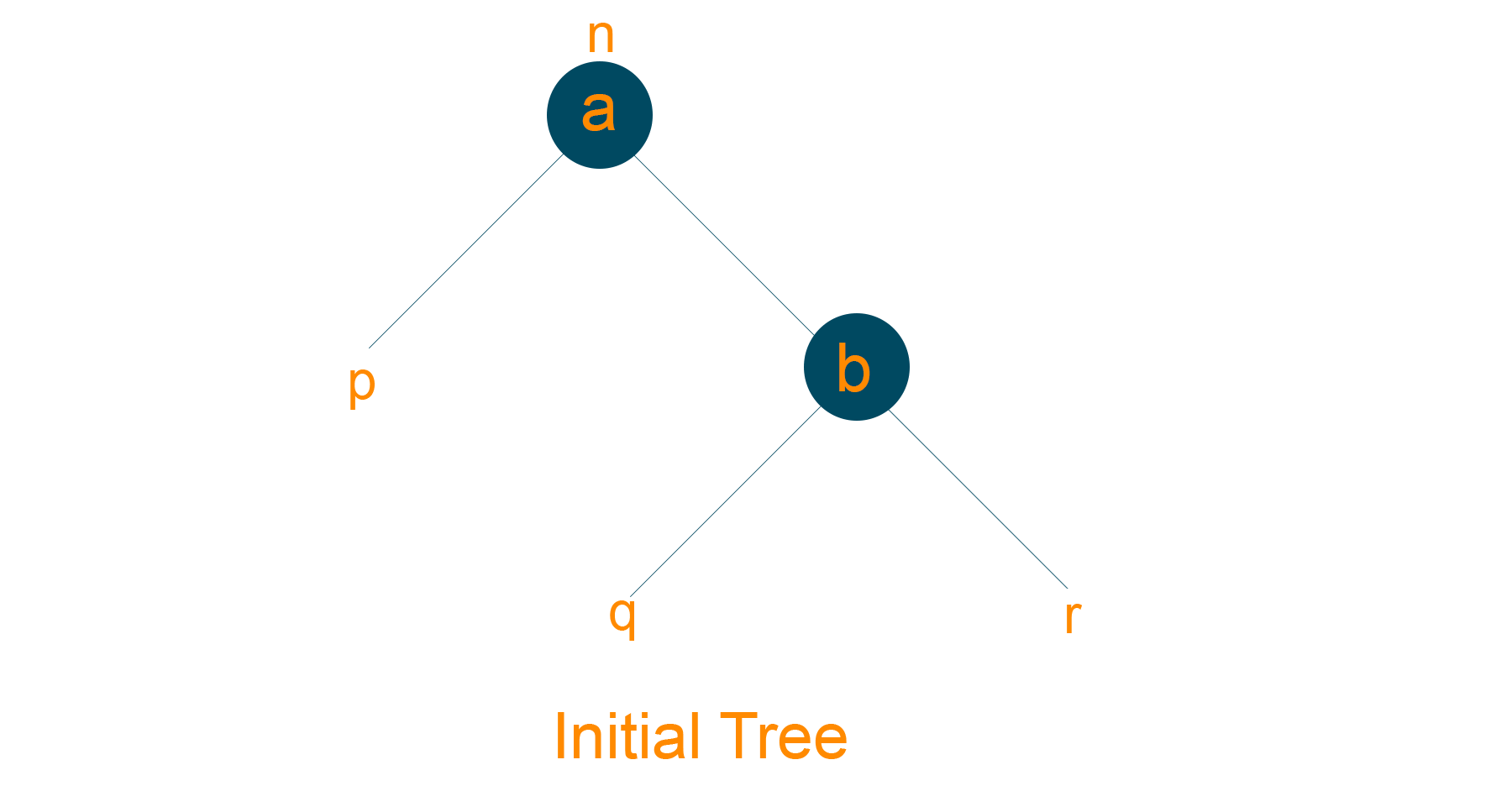
- Assign ‘a’ as a parent node of the left subtree of ‘b’, if ‘b’ has a left subtree.

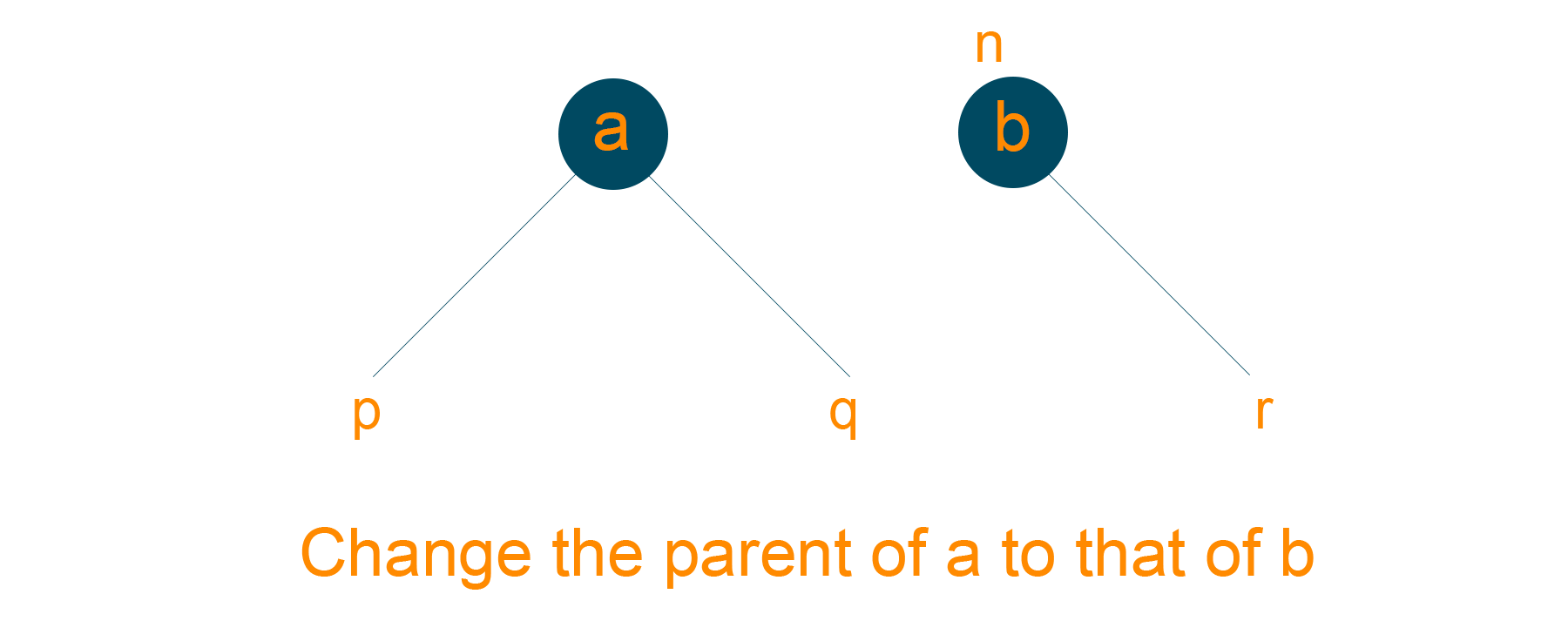
- Assign ‘b’ as the root of the tree if the parent node of ‘a’ is NULL
- Assign ‘b’ as the left child of ‘n’, if ‘a’ is the left child of ‘n’
- Assign ‘b’ as the right child of ‘n’, if ‘a’ is right child of ‘n’
- Make ‘b’ as the parent node of ‘a’

2) Right Rotation
The nodes on the left of the tree are transformed on the right node is called the left rotation. Look at the below algorithm for understanding.
Algorithm
- Consider the below given red-black tree

- Assign ‘b’ as the parent node of the right subtree of ‘a’, if ‘a’ has a right subtree

- Assign ‘a’ as the root of the tree if the parent of ‘b’ is NULL
- Assign ‘a’ as the right child of ‘n’, if ‘b’ is the right child of ‘n’.
- Assign ‘a’ as the left child of ‘n’, if ‘b’ is the right child of ‘n’
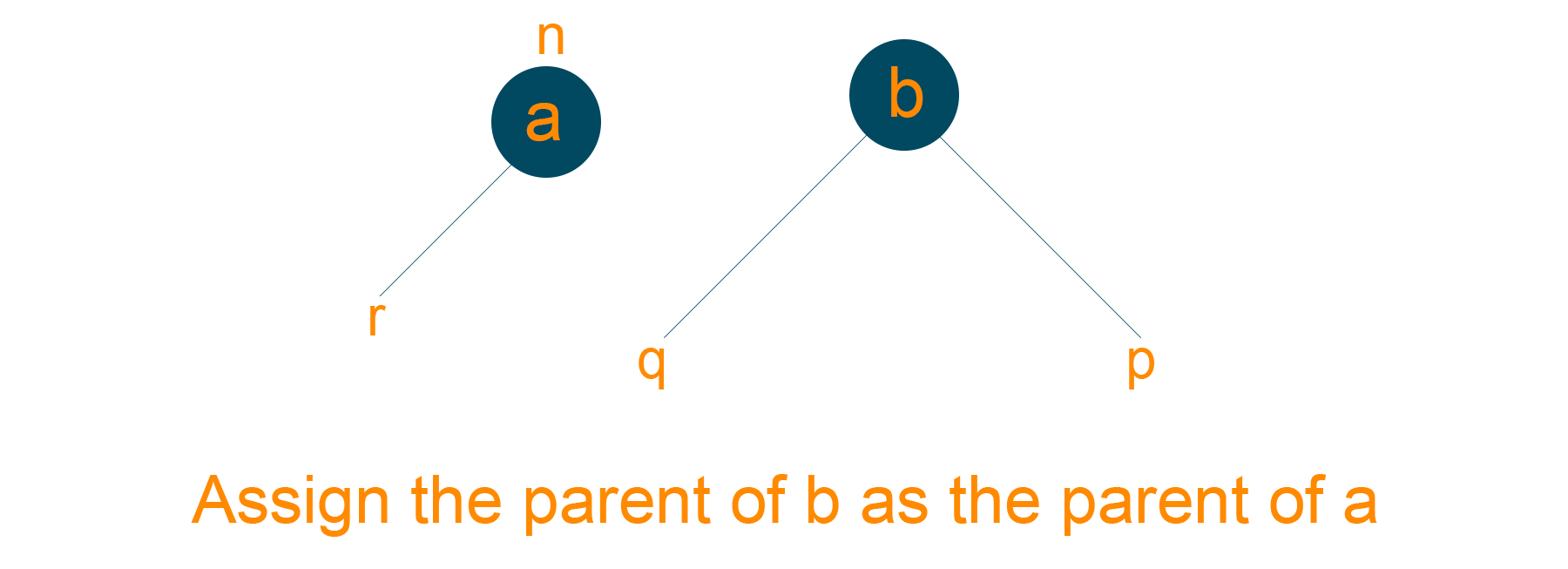
- Make ‘a’ as the parent node of ‘b’
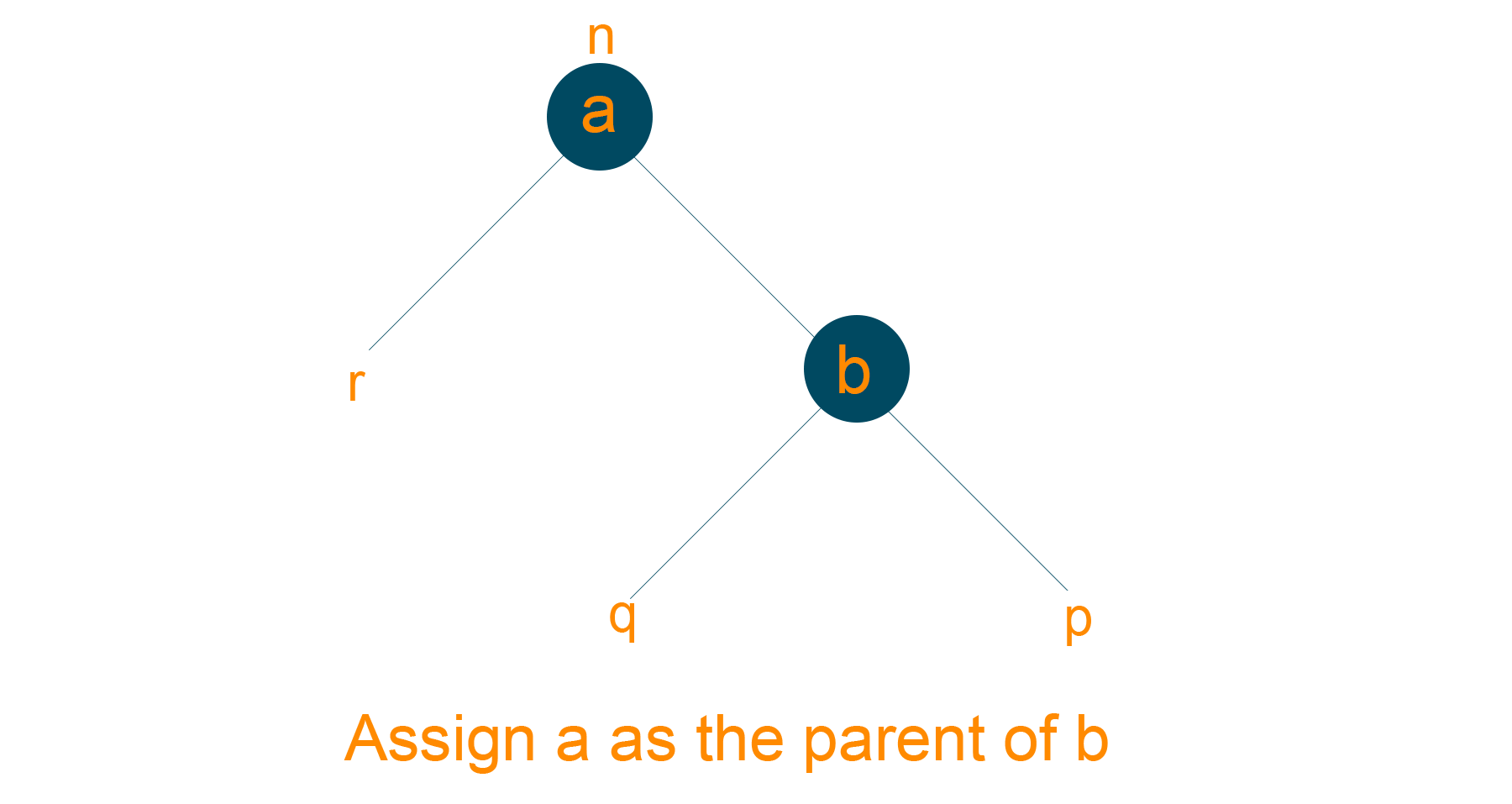
3) Right-Left and Left-Right Rotations
In right-left rotation, first, you perform right rotation followed by a left rotation.

In left-right rotation, first, you perform left rotation followed by right rotation
Operations in Red-Black Tree
There are two operations performed in Red-Black Tree:
- Insertion Operation
- Deletion Operation
1) Insertion Operation
When you insert a new node in the tree, it will always be inserted as Red Node. This is because the insertion of a new node does not violate the depth property of the red-black tree. But what if the red node gets attached to the red node? Well, this problem is easier to fix using rotation rather than violating the depth property of the tree. Later, if the tree properties are violated then the red-black tree undergoes the following operations:
- Recolor
- Rotation
Algorithm For Insertion of the Node
Let ‘x’ be the root node of the tree and ‘y’ be the leaf node If the tree is empty, add NewNode as the root node and black in color Else, repeat the below steps till we reach the leaf of the tree Compare NewNode with RootNode If NewNode is greater than RootNode, traverse to the right subtree Otherwise, traverse through the left subtree Assign parent of leaf to parent of NewNode If LeafNode is greater than NewNode, assign NewNode as RightChild Otherwise, assign NewNode as LeftChild Assign Null to LeftChild and RightChild of NewNode Assign NewNode as Red color Apply InsertionFix Algorithm if the property of the red-black tree is violated
InsertionFix Algorithm to Maintain the Red-Black Tree Property
If parent ‘n’ of NewNode is Red then: If ‘n’ is the LeftChild of GrandParent ‘gp’ of ‘m’ then Case 1: If RightChild of ‘gp’ is Red color, set color of both children of ‘gp’ as Black color and ‘gp’ as Red Color Assign ‘gp’ to NewNode Case 2: If NewNode is RightChild of ‘n’ then, assign ‘n’ to NewNode Left-Rotate NewNode Case 3: Assign ‘n’ as Black and ‘gp’ as Red Right-Rotate ‘gp’ Otherwise, do the following If LeftChild of ‘gp’ of ‘z’ is Red color, then set both children of ‘gp’ as Black color and ‘gp’ as Red color Assign ‘gp’ to NewNode If NewNode is LeftChild of ‘n’ then, assign ‘n’ to NewNode and Right Rotate NewNode Set ‘n’ as Black color and ‘gp’ as Red color Left-Rotate ‘gp’ Set Root of the tree as Black color
Example
Insert node ‘4’ inside an empty tree. As discussed, the first inserted element is always the root node and black in color

Now, insert node ‘20’ inside the tree. As 20 > 4, it will be inserted as the right subtree of the root node and red in color

Now, insert node ‘31’ inside the tree. As 31> 20, it will be the right child of parent node ‘20’. Node ’31’ is red in color and according to the property of the red-black tree, no two red color nodes can be together and therefore we undergo the RR rotation to regain the balance of the tree.
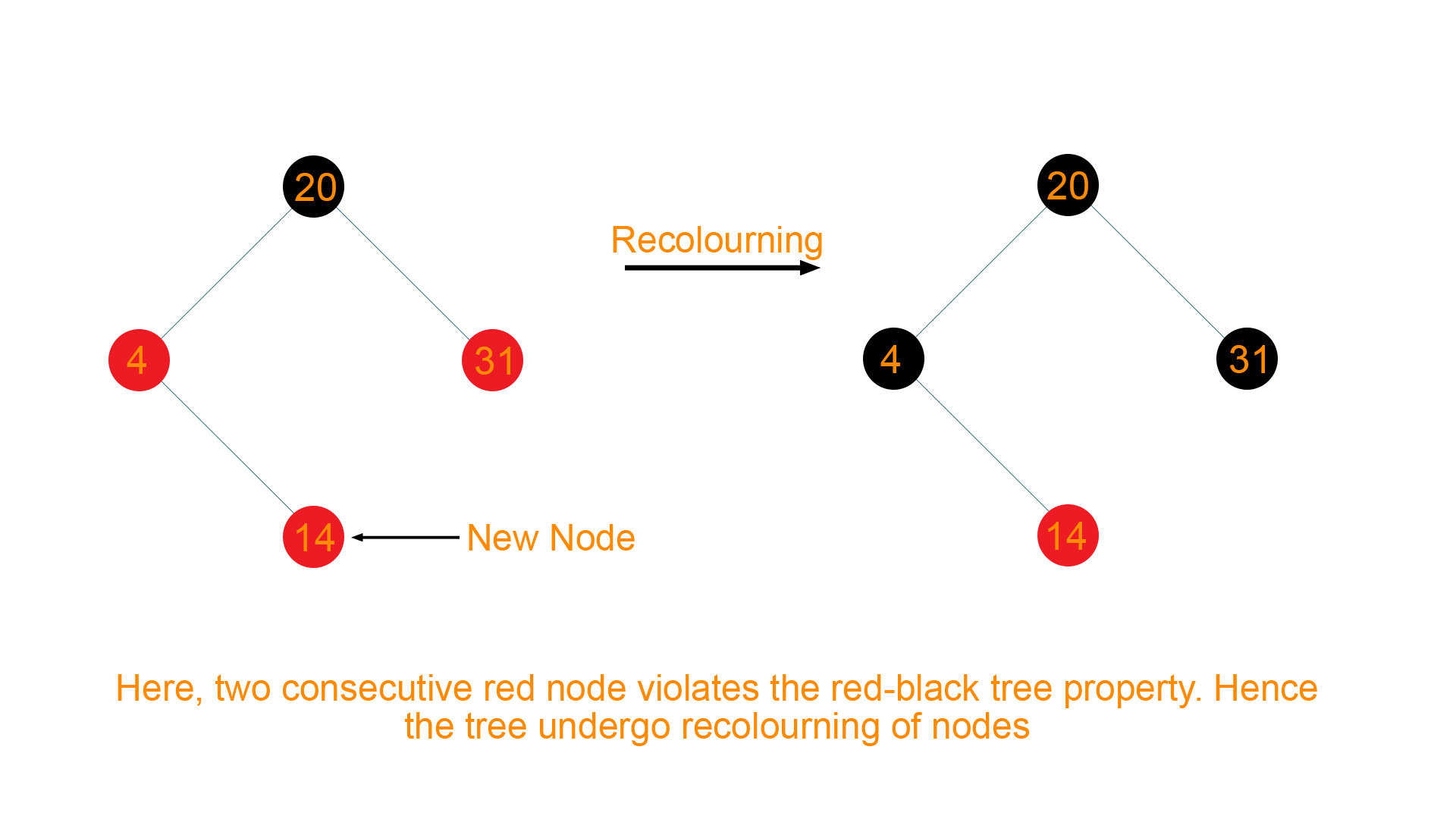
Now, insert node ‘14’ inside the tree. As 14> 4 but 14<20, node ‘14’ will be the right child of node ‘4’. Again, the red-black tree property is violated because you have two consecutive red color nodes. Hence, we perform the recoloring in the tree which results in a red-colored parent node. So we simple color it black colored as shown below
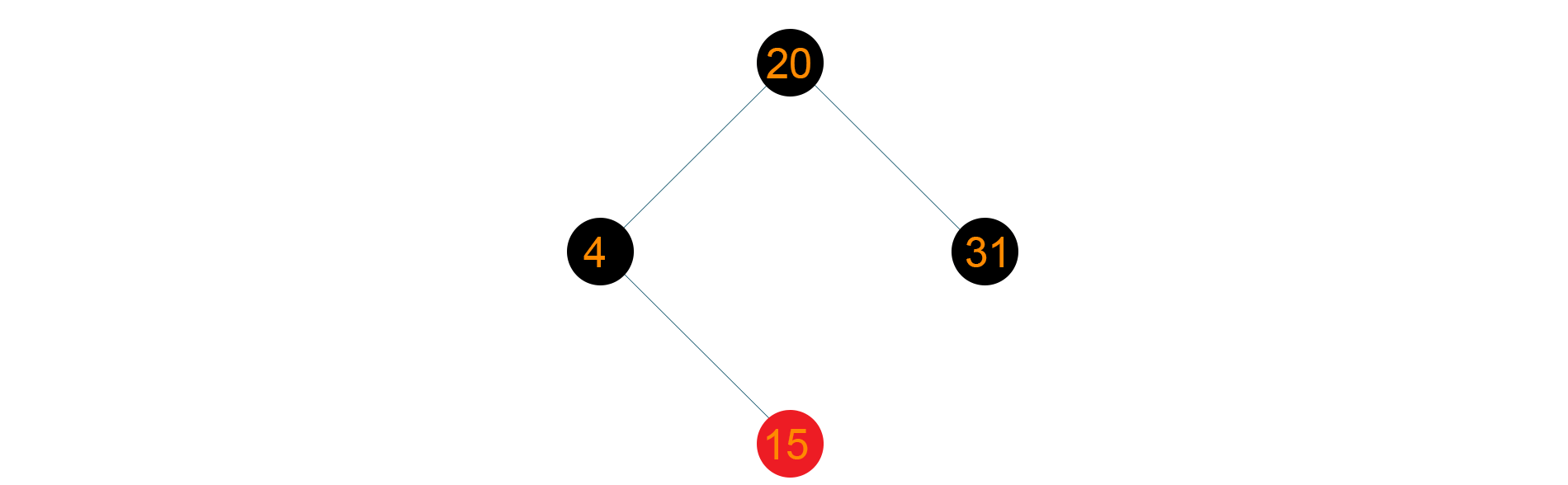
Therefore the final tree structure will be as given below:
Deletion Operation
When you delete a node from the tree, there are possibilities that you violate the red-black tree property. Therefore, after removing the node from the tree, make sure you balance the tree by following the properties of the tree.
Algorithm for Deleting a Node
Save the color of DeletingNode in OriginalColor If LeftChild of DeletingNode is Null Assign the RightChild of DeletingNode to be ‘a’ Transplant DeletingNode with ‘a’ Otherwise, if the RighChild of DeletingNode is Null Assign the LeftChild of DeletingNode into ‘a’ Transplant DeletingNode with ‘a’ Otherwise Assign the minimum of Right-Subtree of DeletingNode into ‘b’ Save the color of ‘b’ in OriginalColor Assign the RightChild of ‘b’ into ‘a’ If ‘b’ is a child of DeletingNode, then set the parent of ‘a’ as ‘b’ Otherwise, transplant ‘b’ with RightChild of ‘b’ Transplant DeletingNode with ‘b’ Set color of ‘b’ with OriginalColor Call DeletionFix if the OriginalColor is Black
When the DeletingNode is black in color, it violates the red-black tree property. This scenario can be corrected by assuming that the node ‘a’ is had extra black. Therefore, node ‘a’ is neither Red nor Black rather it is either double black or black and red at the same time. Hence, the red-black tree property is violated.
Therefore, the extra black can be removed if
- It reached the RootNode
- If ‘a’ points to the red-black node. In this case, ‘a’ is colored, Black
- Required rotations and recoloring is performed
DeletionFix Algorithm to Maintain the Red-Black Tree Property
Repeat the following until the ‘a’ is not the RootNode of the tree and ‘a’ is not the Black colored If ‘a’ is the LeftChild of its parent then, Assign ‘n’ to the sibling of ‘a’ If RightChild of the parent of ‘a’ is Red Case 1: Set RightChild of the parent of ‘a’ as Black color Set parent of ‘a’ as Red Color Left-Rotate the parent of ‘a’ Assign the RightChild of the parent of ‘a’ to ‘n’ If RightChild and the LeftChild of ‘n’ is Black in color Case 2: Set ‘n’ as Red color Assign parent of ‘a’ to ‘a’ Otherwise, if the RightChild of ‘n’ is Black in color Case 3: Set the LeftChild of ‘n’ as Black color Set ‘n’ as Red color Right-rotate ‘n’ Assign the RightChild of the parent of ‘a’ to ‘n’ If all of the above cases don’t occur, then do the following Case 4: Set color of ‘n’ as the color of the parent of ‘a’ Set parent of ‘a’ as Black color Set RightChild ‘n’ as Black color Left-rotate the parent of ‘a’ Set ‘a’ as RootNode of tree Repeat the same steps as above by interchanging the right to left and vice versa Set ‘a’ as Black color
Example
Consider the below given red-black tree
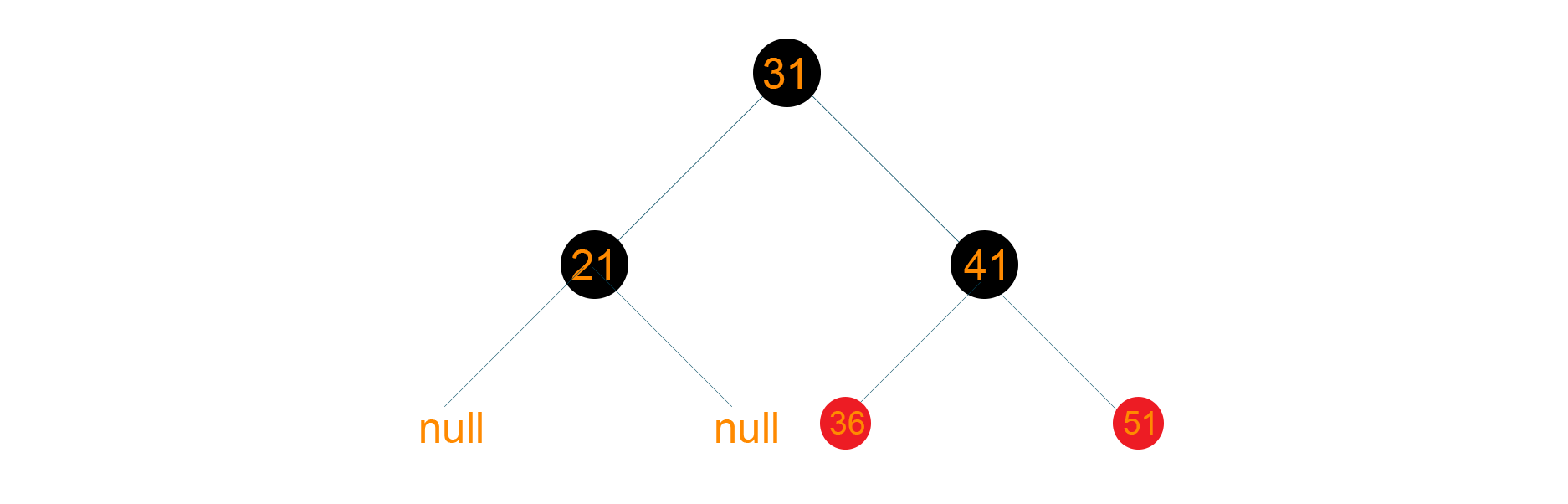
Now we want to delete 21 from the above tree. When node ‘21’ is deleted, it will be replaced by Null, so eventually Null will become double black as shown below
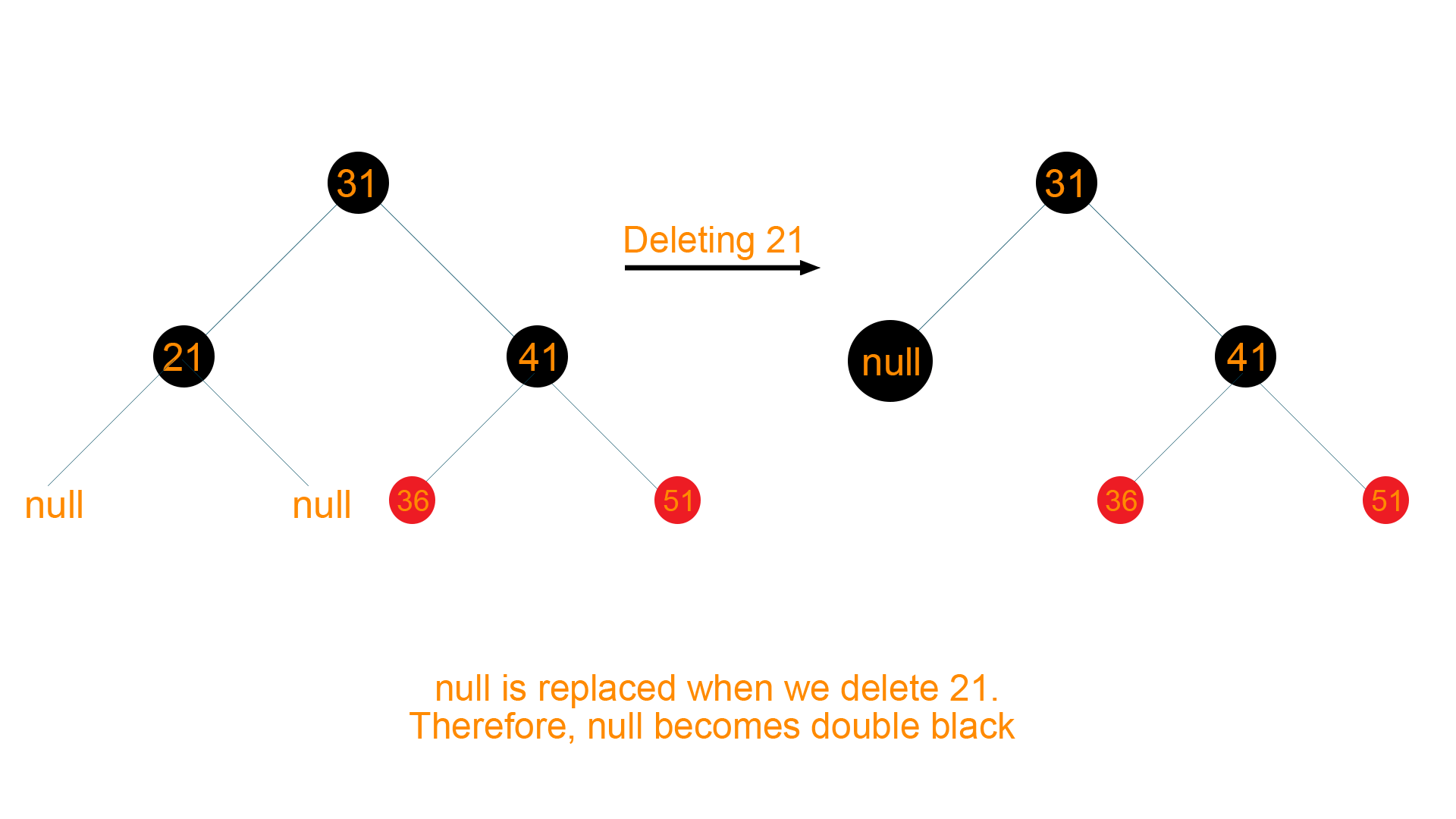
Now according to the algorithm of deletion, sibling of DeletingNode i.e Node ‘41’ is black colored with at least one red-colored child i.e. Node ‘36’ and Node ‘51’. Therefore, it will undergo RR rotation to retain the balance of the tree as shown below
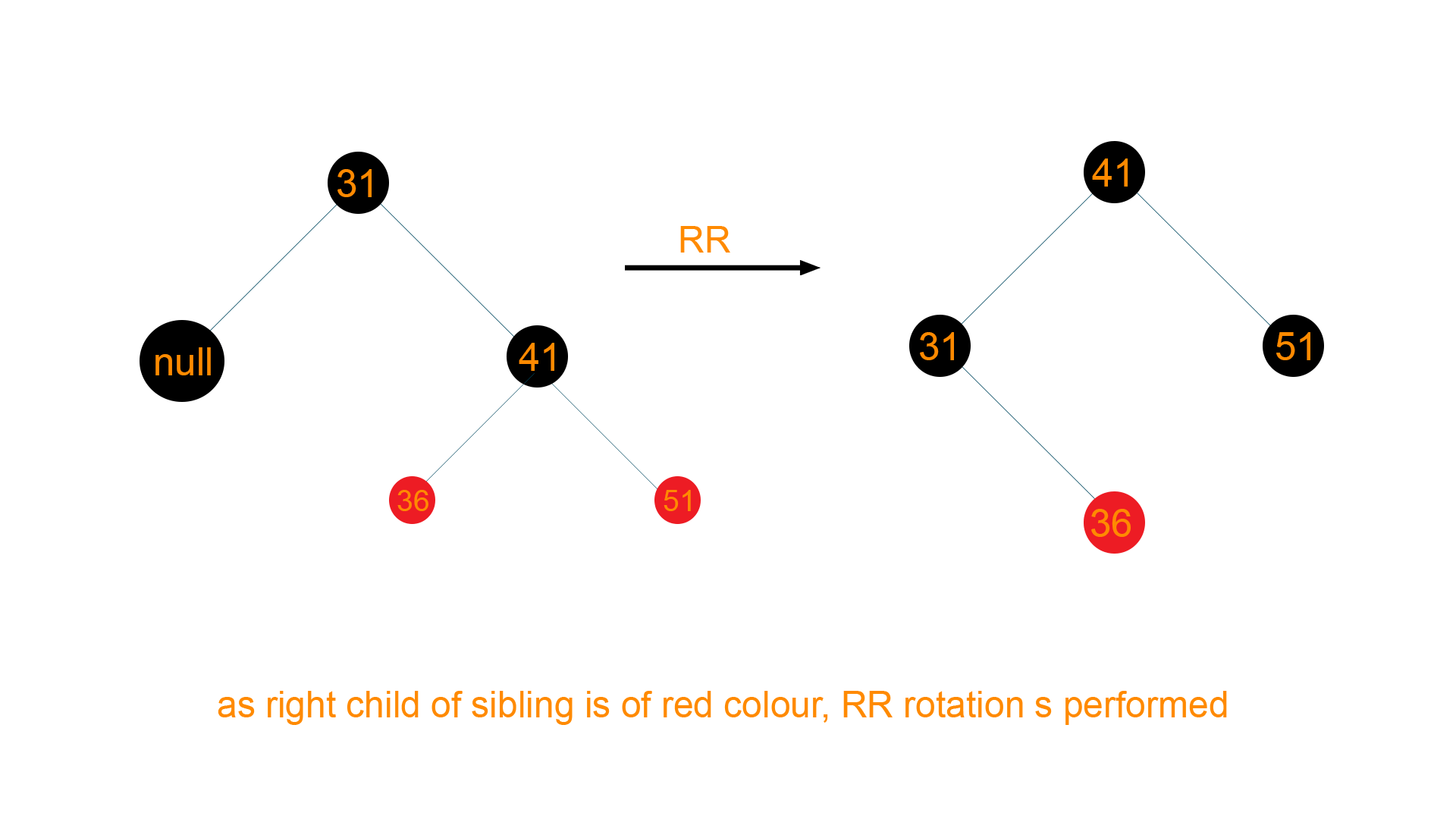
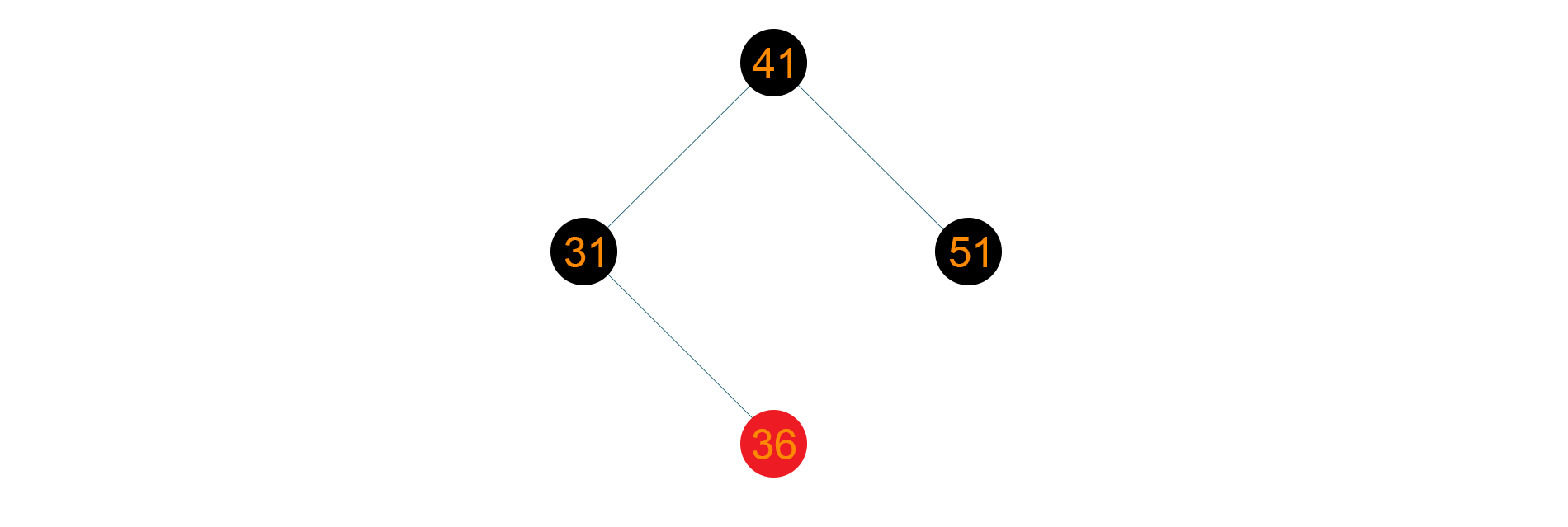
Hence, the final tree structure will be as given below
Python Code for Red-Black Tree
# Define Node class Node(): def __init__(self,val): self.val = val # Value of Node self.parent = None # Parent of Node self.left = None # Left Child of Node self.right = None # Right Child of Node self.color = 1 # Red Node as new node is always inserted as Red Node # Define R-B Tree class RBTree(): def __init__(self): self.NULL = Node ( 0 ) self.NULL.color = 0 self.NULL.left = None self.NULL.right = None self.root = self.NULL # Insert New Node def insertNode(self, key): node = Node(key) node.parent = None node.val = key node.left = self.NULL node.right = self.NULL node.color = 1 # Set root colour as Red y = None x = self.root while x != self.NULL : # Find position for new node y = x if node.val < x.val : x = x.left else : x = x.right node.parent = y # Set parent of Node as y if y == None : # If parent i.e, is none then it is root node self.root = node elif node.val < y.val : # Check if it is right Node or Left Node by checking the value y.left = node else : y.right = node if node.parent == None : # Root node is always Black node.color = 0 return if node.parent.parent == None : # If parent of node is Root Node return self.fixInsert ( node ) # Else call for Fix Up def minimum(self, node): while node.left != self.NULL: node = node.left return node # Code for left rotate def LR ( self , x ) : y = x.right # Y = Right child of x x.right = y.left # Change right child of x to left child of y if y.left != self.NULL : y.left.parent = x y.parent = x.parent # Change parent of y as parent of x if x.parent == None : # If parent of x == None ie. root node self.root = y # Set y as root elif x == x.parent.left : x.parent.left = y else : x.parent.right = y y.left = x x.parent = y # Code for right rotate def RR ( self , x ) : y = x.left # Y = Left child of x x.left = y.right # Change left child of x to right child of y if y.right != self.NULL : y.right.parent = x y.parent = x.parent # Change parent of y as parent of x if x.parent == None : # If x is root node self.root = y # Set y as root elif x == x.parent.right : x.parent.right = y else : x.parent.left = y y.right = x x.parent = y # Fix Up Insertion def fixInsert(self, k): while k.parent.color == 1: # While parent is red if k.parent == k.parent.parent.right: # if parent is right child of its parent u = k.parent.parent.left # Left child of grandparent if u.color == 1: # if color of left child of grandparent i.e, uncle node is red u.color = 0 # Set both children of grandparent node as black k.parent.color = 0 k.parent.parent.color = 1 # Set grandparent node as Red k = k.parent.parent # Repeat the algo with Parent node to check conflicts else: if k == k.parent.left: # If k is left child of it's parent k = k.parent self.RR(k) # Call for right rotation k.parent.color = 0 k.parent.parent.color = 1 self.LR(k.parent.parent) else: # if parent is left child of its parent u = k.parent.parent.right # Right child of grandparent if u.color == 1: # if color of right child of grandparent i.e, uncle node is red u.color = 0 # Set color of childs as black k.parent.color = 0 k.parent.parent.color = 1 # set color of grandparent as Red k = k.parent.parent # Repeat algo on grandparent to remove conflicts else: if k == k.parent.right: # if k is right child of its parent k = k.parent self.LR(k) # Call left rotate on parent of k k.parent.color = 0 k.parent.parent.color = 1 self.RR(k.parent.parent) # Call right rotate on grandparent if k == self.root: # If k reaches root then break break self.root.color = 0 # Set color of root as black # Function to fix issues after deletion def fixDelete ( self , x ) : while x != self.root and x.color == 0 : # Repeat until x reaches nodes and color of x is black if x == x.parent.left : # If x is left child of its parent s = x.parent.right # Sibling of x if s.color == 1 : # if sibling is red s.color = 0 # Set its color to black x.parent.color = 1 # Make its parent red self.LR ( x.parent ) # Call for left rotate on parent of x s = x.parent.right # If both the child are black if s.left.color == 0 and s.right.color == 0 : s.color = 1 # Set color of s as red x = x.parent else : if s.right.color == 0 : # If right child of s is black s.left.color = 0 # set left child of s as black s.color = 1 # set color of s as red self.RR ( s ) # call right rotation on x s = x.parent.right s.color = x.parent.color x.parent.color = 0 # Set parent of x as black s.right.color = 0 self.LR ( x.parent ) # call left rotation on parent of x x = self.root else : # If x is right child of its parent s = x.parent.left # Sibling of x if s.color == 1 : # if sibling is red s.color = 0 # Set its color to black x.parent.color = 1 # Make its parent red self.RR ( x.parent ) # Call for right rotate on parent of x s = x.parent.left if s.right.color == 0 and s.right.color == 0 : s.color = 1 x = x.parent else : if s.left.color == 0 : # If left child of s is black s.right.color = 0 # set right child of s as black s.color = 1 self.LR ( s ) # call left rotation on x s = x.parent.left s.color = x.parent.color x.parent.color = 0 s.left.color = 0 self.RR ( x.parent ) x = self.root x.color = 0 # Function to transplant nodes def __rb_transplant ( self , u , v ) : if u.parent == None : self.root = v elif u == u.parent.left : u.parent.left = v else : u.parent.right = v v.parent = u.parent # Function to handle deletion def delete_node_helper ( self , node , key ) : z = self.NULL while node != self.NULL : # Search for the node having that value/ key and store it in 'z' if node.val == key : z = node if node.val <= key : node = node.right else : node = node.left if z == self.NULL : # If Kwy is not present then deletion not possible so return print ( "Value not present in Tree !!" ) return y = z y_original_color = y.color # Store the color of z- node if z.left == self.NULL : # If left child of z is NULL x = z.right # Assign right child of z to x self.__rb_transplant ( z , z.right ) # Transplant Node to be deleted with x elif (z.right == self.NULL) : # If right child of z is NULL x = z.left # Assign left child of z to x self.__rb_transplant ( z , z.left ) # Transplant Node to be deleted with x else : # If z has both the child nodes y = self.minimum ( z.right ) # Find minimum of the right sub tree y_original_color = y.color # Store color of y x = y.right if y.parent == z : # If y is child of z x.parent = y # Set parent of x as y else : self.__rb_transplant ( y , y.right ) y.right = z.right y.right.parent = y self.__rb_transplant ( z , y ) y.left = z.left y.left.parent = y y.color = z.color if y_original_color == 0 : # If color is black then fixing is needed self.fixDelete ( x ) # Deletion of node def delete_node ( self , val ) : self.delete_node_helper ( self.root , val ) # Call for deletion # Function to print def __printCall ( self , node , indent , last ) : if node != self.NULL : print(indent, end=' ') if last : print ("R----",end= ' ') indent += " " else : print("L----",end=' ') indent += "| " s_color = "RED" if node.color == 1 else "BLACK" print ( str ( node.val ) + "(" + s_color + ")" ) self.__printCall ( node.left , indent , False ) self.__printCall ( node.right , indent , True ) # Function to call print def print_tree ( self ) : self.__printCall ( self.root , "" , True ) if __name__ == "__main__": bst = RBTree() bst.insertNode(10) bst.insertNode(20) bst.insertNode(30) bst.insertNode(5) bst.insertNode(4) bst.insertNode(2) bst.print_tree() print("\nAfter deleting an element") bst.delete_node(2) bst.print_tree()
Output
R---- 20(BLACK)
L---- 5(RED)
| L---- 4(BLACK)
| | L---- 2(RED)
| R---- 10(BLACK)
R---- 30(BLACK)
After deleting an element
R---- 20(BLACK)
L---- 5(RED)
| L---- 4(BLACK)
| R---- 10(BLACK)
R---- 30(BLACK)
Time Complexity
For insertion, deletion, and search operation, the time complexity for the red-black tree is logarithmic function i.e. O(log n) where n is the total number of nodes in the red-black tree. Whereas, the space complexity of the red-black tree is O(n).
Difference between Red-Black Tree and AVL Tree
|
Red-Black Tree |
AVL Tree |
|
It does not provide efficient searching as red-black tree are roughly balanced |
It provides efficient searching as AVL trees are strictly balanced
|
|
Insertion and deletion operation is easier as require less number of rotation to balance the tree |
Insertion and deletion operation is difficult as require more number of rotation to balance the tree |
|
The nodes are either red or black in color |
The nodes have no colors
|
|
It does not contain any balance factor to balance the height of the tree |
It contains the balance factor to maintain the difference in the height of the tree. |
|
Mostly used for insertion and deletion operations |
Mostly used for searching operations |
Advantages of Red-Black Tree
- Red-black tree balance the height of the binary tree
- Red-black tree takes less time to structure the tree by restoring the height of the binary tree
- The time complexity for search operation is O(log n)
- It has comparatively low constants in a wide range of scenarios
Disadvantages of Red-Black Tree
- Relatively complicated to implement
- The red-black tree is not rigidly balanced in comparison to the AVL tree
Applications of Red-Black Tree
- A red-black tree is used to implement the finite maps
- It is most important to implement the Java Libraries Packages like java.util.TreeSet and java.util.TreeMap
- A red-black tree is used while building the Linux kernel
- A red-black tree is used to implement the standard template library in C++
- It is used to implement the CPU scheduling algorithm like “completely fair scheduler” in Linux.
- A red-black tree is used in reducing the time complexity in the K-mean clustering algorithm
- It is used in MySQL for table indexing
- A red-black tree is used in Computation Geometry Data structure
- It is useful to keep track of the virtual memory segments for the process
- Hashmap data structure makes use of the red-black tree to store the key-value pair instead of linked-list for the faster search operation
Conclusion
The red-black tree is one of the members of the binary search tree which helps to maintain the height of the binary tree just like the AVL tree. Every node in the binary search tree is colored either red or black which further helps to maintain the properties of the tree and provides an effective and efficient method for insertion and deletion operations of the node in the binary tree by undergoing a fewer rotation. Therefore it is important to understand and make use of the red-black tree to enhance the searching time complexity of the binary search tree by preventing the tree from skewing. For more details, please refer to our extensive tutor program designed by experts at Favtutor.








