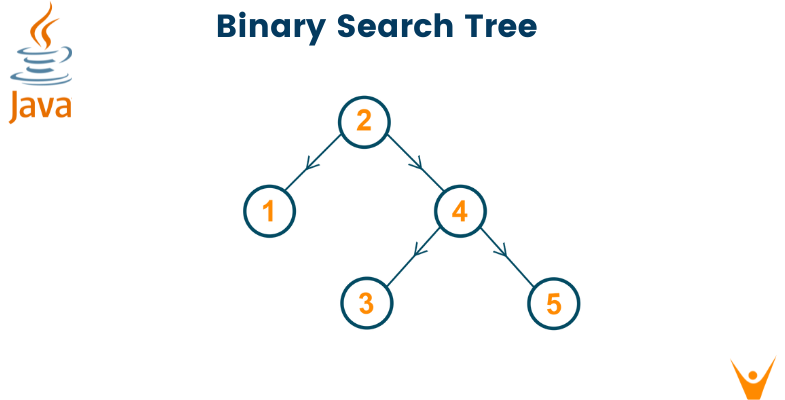
Trees might just be one of the most important topics that are asked during technical interviews. In fact, trees have some of the best applications amongst all of the data structures during software development (both while getting hired and when one is working on a technical project!). Trees themselves have many types, though the best known amongst them might probably be the binary tree. What are all of these terms? Well, let's clear them out one by one.
Some General Terminology of Trees
Some general terminology that one needs to understand to be able to follow the discussion on binary trees (and in turn, binary search trees) have been described below:-
Node - Every unit that makes up the tree is called a node. Each node holds some data and points towards other nodes in the tree. For a binary tree, each node has two children - one left child and one right child.
Children - The successors to some node in the tree. With the exception of leaves, all nodes in the binary tree generally have at least one or two children. All children are linked to its parent with a one-way pointer.
Parent - The predecessor to some node in the tree. With the exception of the root, all nodes in the binary tree have a parent.
Root - Like every real-world tree, trees in the digital world take stem from a root. The root is the starting node for a tree from which all of the nodes are added as children. The root does not have a parent since it is the "first node" in the tree.
Leaves - Like a real-world tree, every tree in the digital world has leaves. These leaves are the ultimate nodes in the tree, marking the terminals of the tree. Leaves do not have any children since they technically mark the "borders" for the points where the tree ends.
Intermediate node - All nodes other than the roots and the leaves in a tree are called intermediate nodes. This is so named because these nodes lie in between the root and the leaves of the tree.
Subtree - A subsection of the entire tree.
These terms are crucial for understanding the functionality of the tree as a data structure since they will be repeatedly used in the next few paragraphs.
What is a Binary Search Tree?
Well, binary search trees or BST are a special variant of trees that come with a very unique condition for filling in the left and right children of every node in the tree. In order to understand the basics of the binary search tree, one needs to understand the basics of a binary tree first. The binary tree is a tree where each node (except the leaves) has two children. Each node can have one parent and a maximum of two children.
A binary search tree extends upon the concept of a binary tree. A binary search tree is set such that:-
1) Every left node is always lesser than its parent node
2) Every right node is always greater than its parent node
At the time of insertion of nodes, the decision about the position of the node is made. These properties help solve a lot of algorithmic challenges, and as such was designed for that purpose. Binary search trees support all operations that can be performed on binary trees, allowing some of the tasks to be done in lesser time.
Java Code to Check if a Tree is a BST or Not
public class BinaryTree { static class Node { //instance variable of Node class public int data; public Node left; public Node right; //constructor public Node(int data) { this.data = data; this.left = null; this.right = null; } } // instance variable of binary tree class public Node root; // constructor for initialise the root to null BYDEFAULT public BinaryTree() { this.root = null; } // method to check the given tree is Binary search tree or not public boolean isBSTOrNot() { return isBSTOrNot(this.root, Integer.MIN_VALUE, Integer.MAX_VALUE); } private boolean isBSTOrNot(Node root, int minValue, int maxValue) { // check for root is not null or not if (root == null) { return true; } // check for current node value with left node value and right node value and recursively check for left sub tree and right sub tree if(root.data >= minValue && root.data <= maxValue && isBSTOrNot(root.left, minValue, root.data) && isBSTOrNot(root.right, root.data, maxValue)){ return true; } return false; } public static void main(String[] args) { // Creating the object of BinaryTree class BinaryTree bt = new BinaryTree(); bt.root= new Node(100); bt.root.left= new Node(90); bt.root.right= new Node(110); bt.root.left.left= new Node(80); bt.root.left.right= new Node(95); System.out.println(bt.isBSTOrNot()); } }
Output:
True
What is Tree Traversal?
All trees can be traversed in three main ways. Each particular approach gives us a different arrangement of nodes. The three main approaches used are:-
1) Preorder - This traversal involves printing the root, then recursively calling the function for the left subtree and the right subtree.
2) Postorder - This traversal involves recursively calling the function for the left subtree and the right subtree and then printing the root.
3) Inorder - This traversal involves recursively calling the function for the left subtree, printing the root, and then recursively calling the function for the right subtree.
All traversals have their own purpose - they are used for getting something done in particular. Preorder traversal helps us copy the contents of the tree which can be used to make a prefix expression. This is especially useful for parsing expression trees - a method used by compilers for segregating symbols and data inside the expression tree. The main use of postorder traversal is to delete a tree in its entirety - from root to the leaves.
Postorder traversal deletes the child nodes before hitting the root, making it ideal for deletion of the tree. Inorder traversal is perhaps one of the most used amongst all the traversal techniques. This is because it is used for printing all the nodes of the tree in ascending order. This can also be modified to print the nodes in descending order. For more details on tree traversals including working codes to put them into action, check out our detailed blog on tree traversal with recursion.
Insertion in a Binary Search Tree
Insertion in a tree should be such that it obeys the main properties of the binary search tree. The basic algorithm should be:-
1) If the node to be inserted is greater than the existing root, move down a level through the right pointer of the root.
2) If the node to be inserted is lesser than the existing root, move down a level through the left pointer of the root.
3) Repeat this process for all nodes till the leaves are reached.
4) Insert the node as the left or right pointer for the leaf (based on its value - if it is smaller than the leaf, it should be inserted as the left pointer; if it is larger than the leaf, it should be inserted as the right pointer)
Detailed Example
Let's say that we have to build a binary search tree from scratch. We can take an assortment of elements and try seeing how they are arranged to be in the exact order inside the tree.
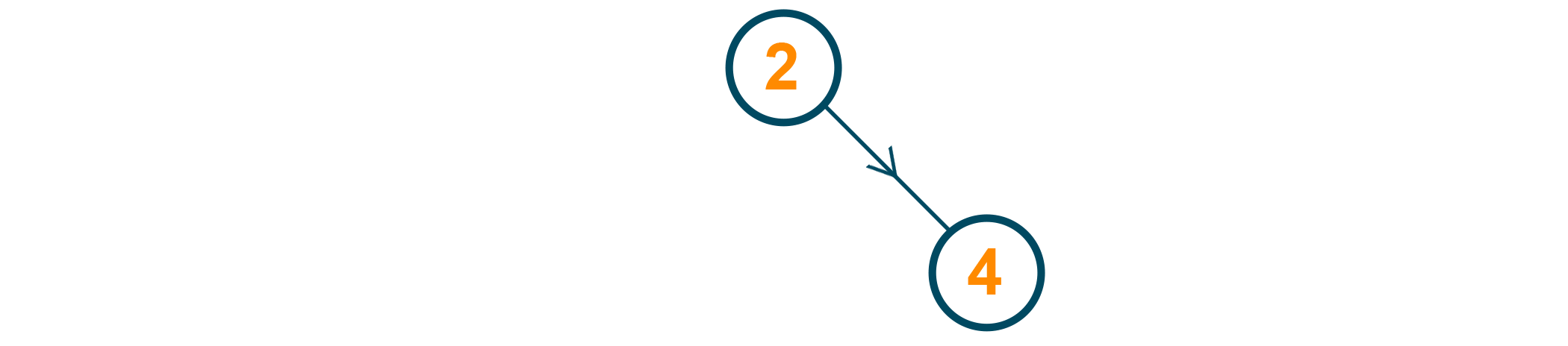
2 is the first node to be inserted, so both of its left and right pointers will be null. This is the root of our binary search tree.
4 is the second node to be inserted. Since 4 is greater than 2, 2's right pointer is attached to 4. Both of 4's pointers will be null. In this case, 2 is the root, while 4 is a leaf of the tree.
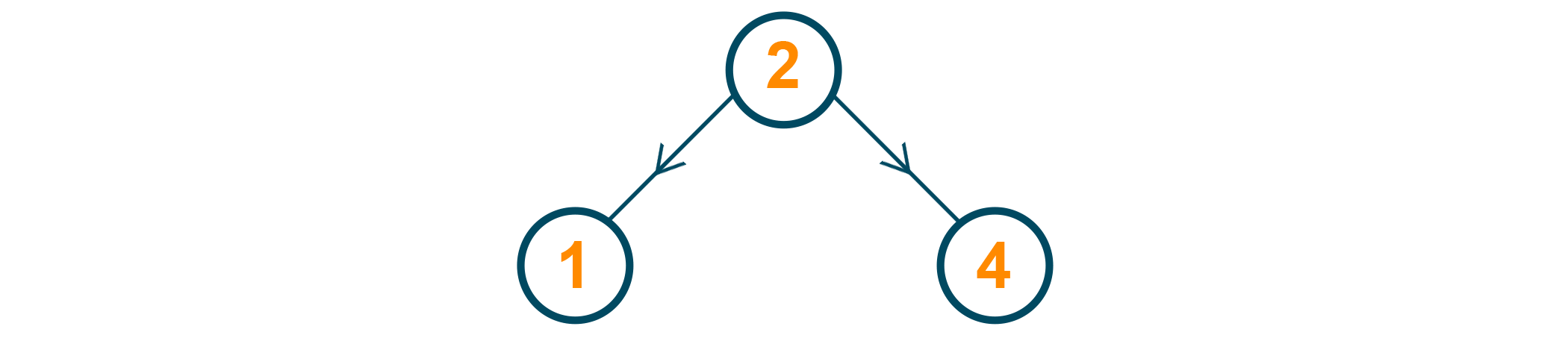
1 is the third node to be inserted. Since 1 is lesser than 2, 2's left pointer is attached to 1. Both of 1's pointers will be null. Both 2 and 4 are leaves now.
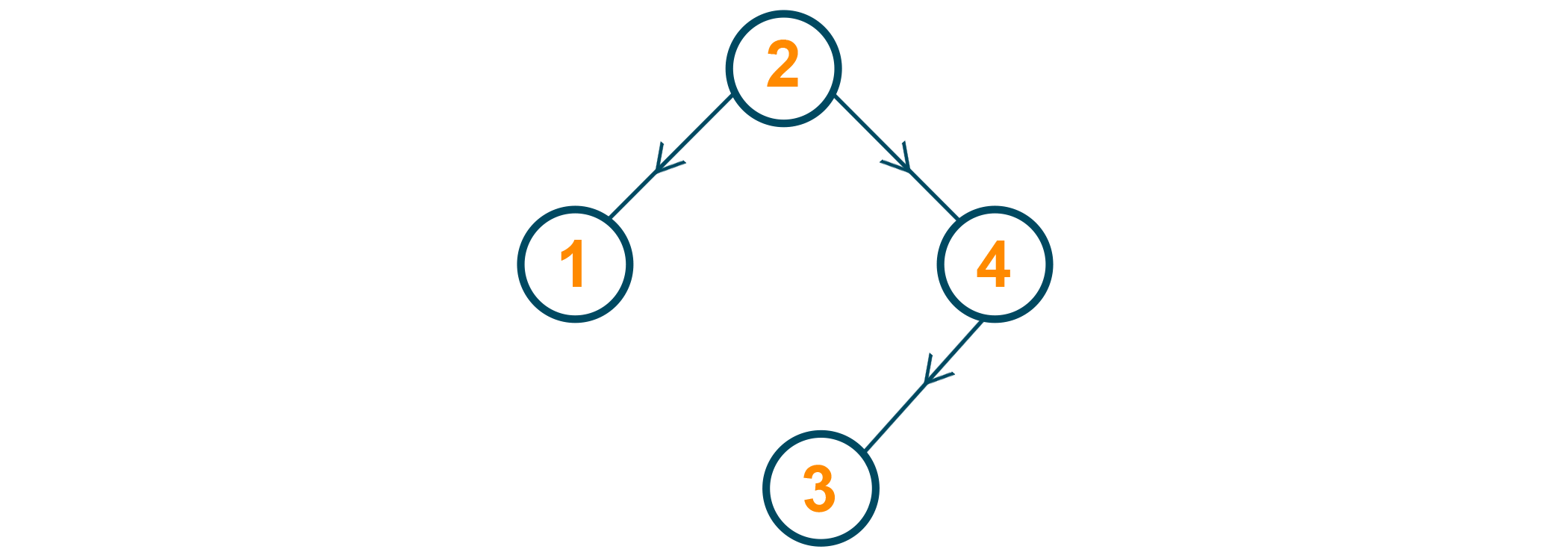
3 is the fourth node to be inserted. Since 3 is greater than 2 but lesser than 4, 3 is inserted as the left child for 4. 4 becomes an intermediate node now, while 3 is a leaf now.
5 is the fifth node to be inserted. Since 5 is greater than both 2 and 4, 5 is inserted as the right child for 4. 5 becomes a leaf in the tree after this step.
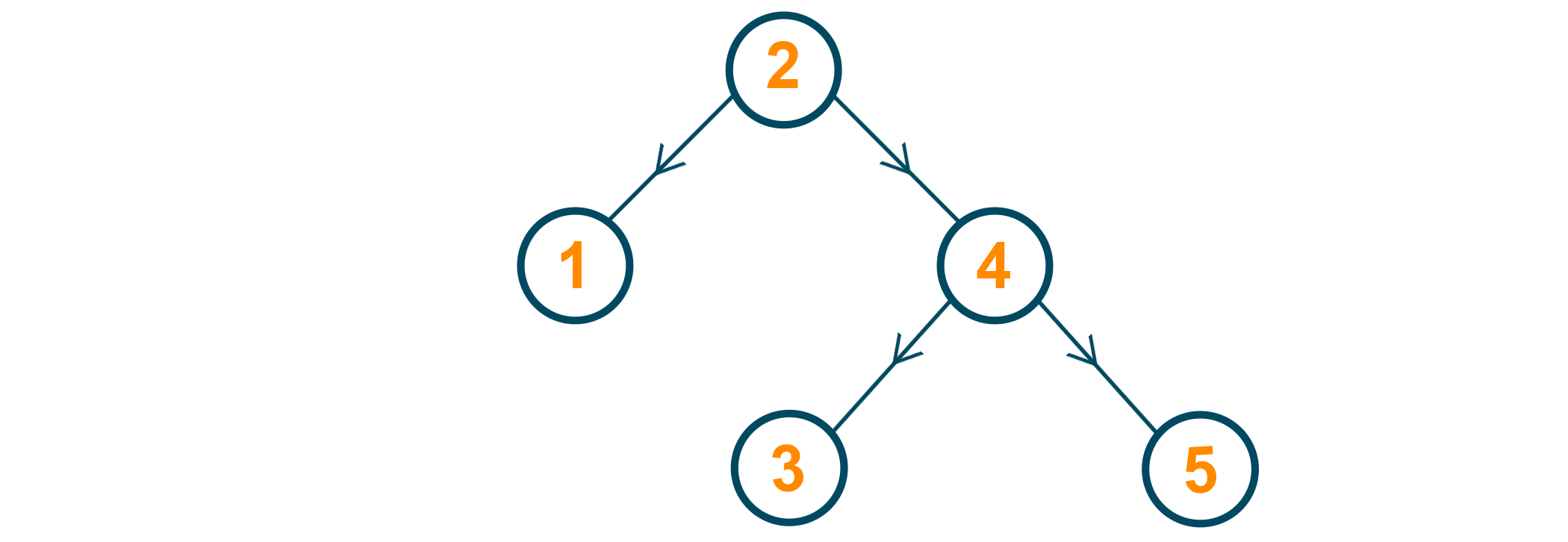
In this way, all of the steps are satisfied while constructing the tree. The left subtree always contains elements lesser than the root, while the right subtree always contains elements greater than the root. Now, this concept applies to both the root as well as the intermediate nodes in the trees as well (carefully think about it for a second!).
Java Program for Insertion in Binary Search Tree
public class BinarySearchTree { public class Node { //instance variable of Node class public int data; public Node left; public Node right; //constructor public Node(int data) { this.data = data; this.left = null; this.right = null; } } // instance variable public Node root; // constructor for initialise the root to null BYDEFAULT public BinarySearchTree() { this.root = null; } // insert method to insert the new Date public void insert(int newData) { this.root = insert(root, newData); } public Node insert(Node root, int newData) { // Base Case: root is null or not if (root == null) { // Insert the new data, if root is null. root = new Node(newData); // return the current root to his sub tree return root; } // Here checking for root data is greater or equal to newData or not else if (root.data >= newData) { // if current root data is greater than the new data then now process the left sub-tree root.left = insert(root.left, newData); } else { // if current root data is less than the new data then now process the right sub-tree root.right = insert(root.right, newData); } return root; } //Traversal public void preorder() { preorder(root); } public void preorder(Node root) { if (root == null) { return; } System.out.print(root.data + " "); preorder(root.left); preorder(root.right); } public static void main(String[] args) { // Creating the object of BinarySearchTree class BinarySearchTree bst = new BinarySearchTree(); // call the method insert bst.insert(2); bst.insert(4); bst.insert(1); bst.insert(3); bst.insert(5); bst.preorder(); } }
Output:
2 1 4 3 5
Deletion from a Binary Search Tree
Deletion is a bit more complicated than insertion because it varies depending on the node that needs to be deleted from the tree.
1) If the node has no children (that is, it is a leaf) - it can simply be deleted from the tree.
Here's an example of a tree-
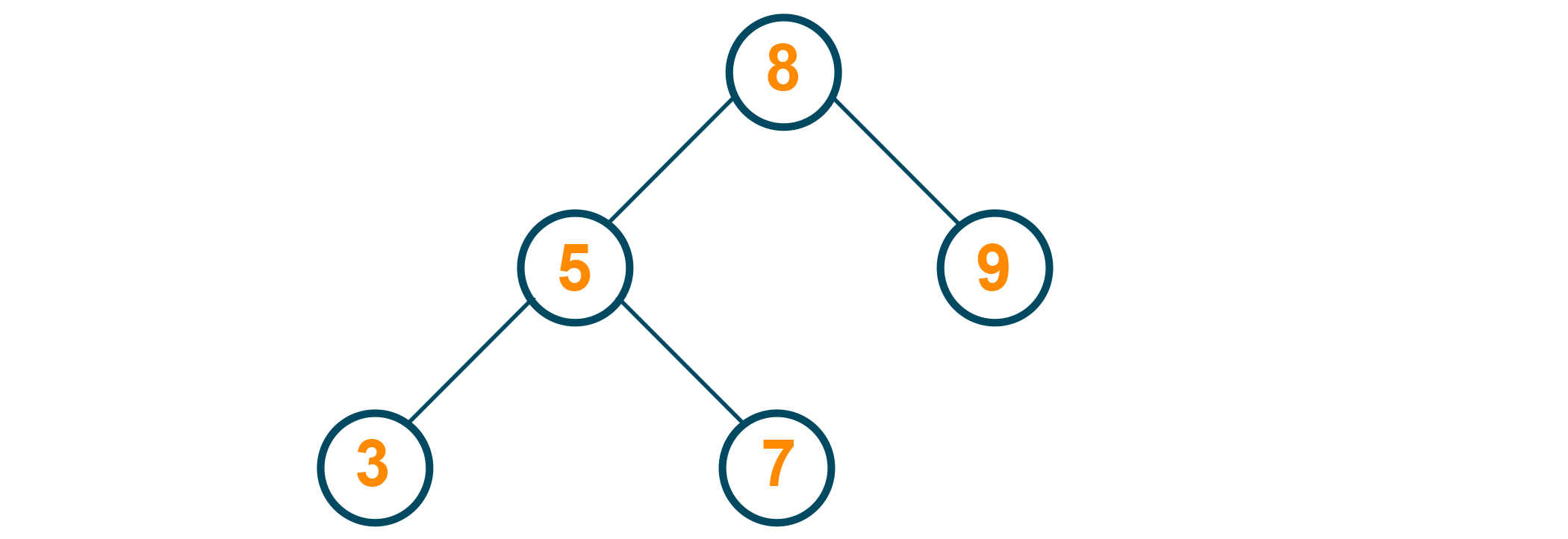
2) If the node has one child, simply delete the node and move the child up to replace it.
Here's an example of a tree-
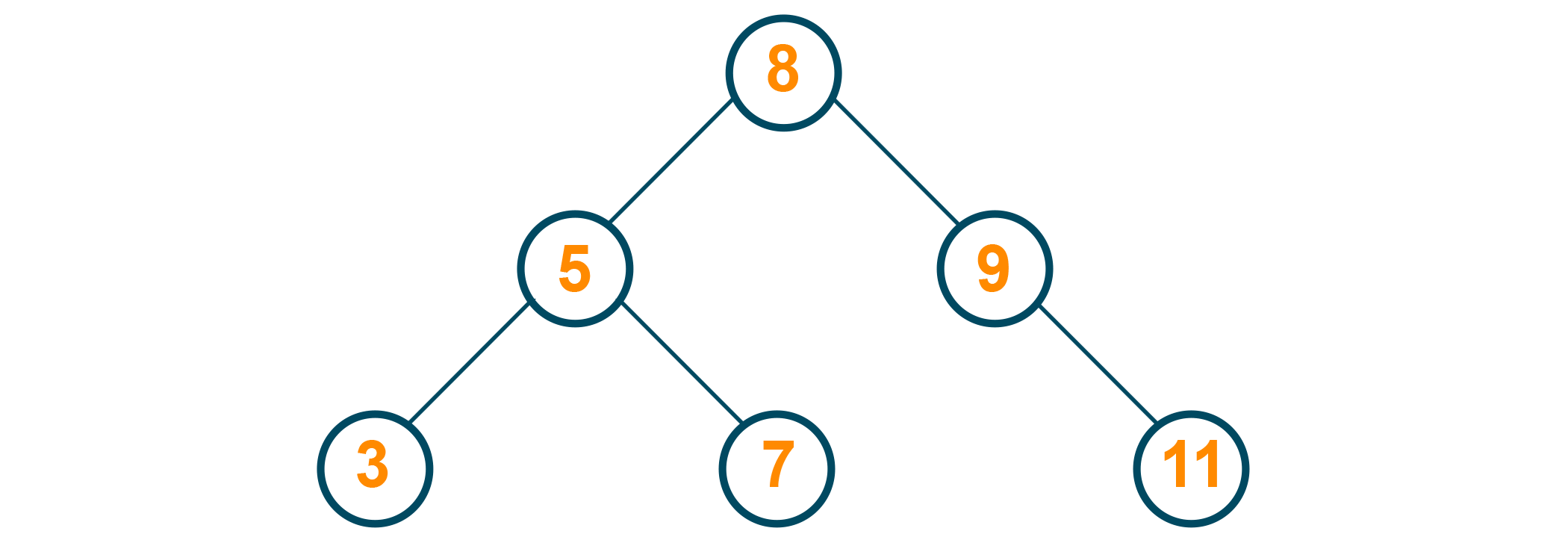
9 is to be deleted from the tree. Here, the successor of 9 (which is 11) is directly attached to 9's predecessor (which is the root)
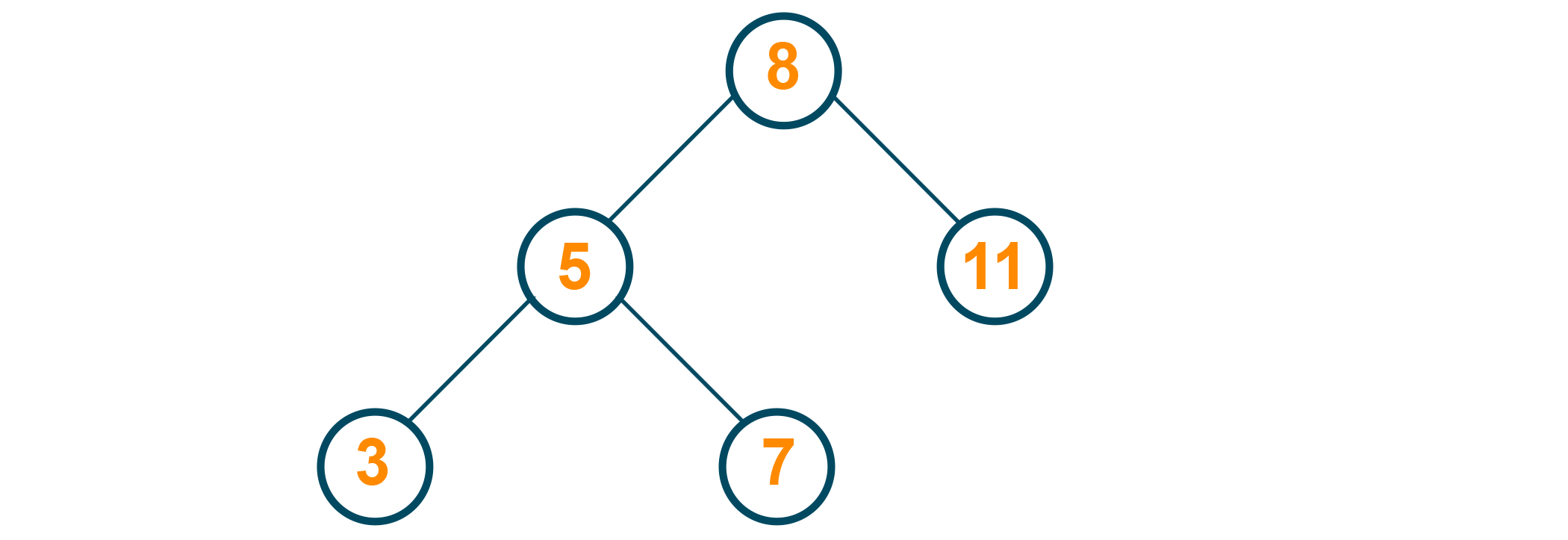
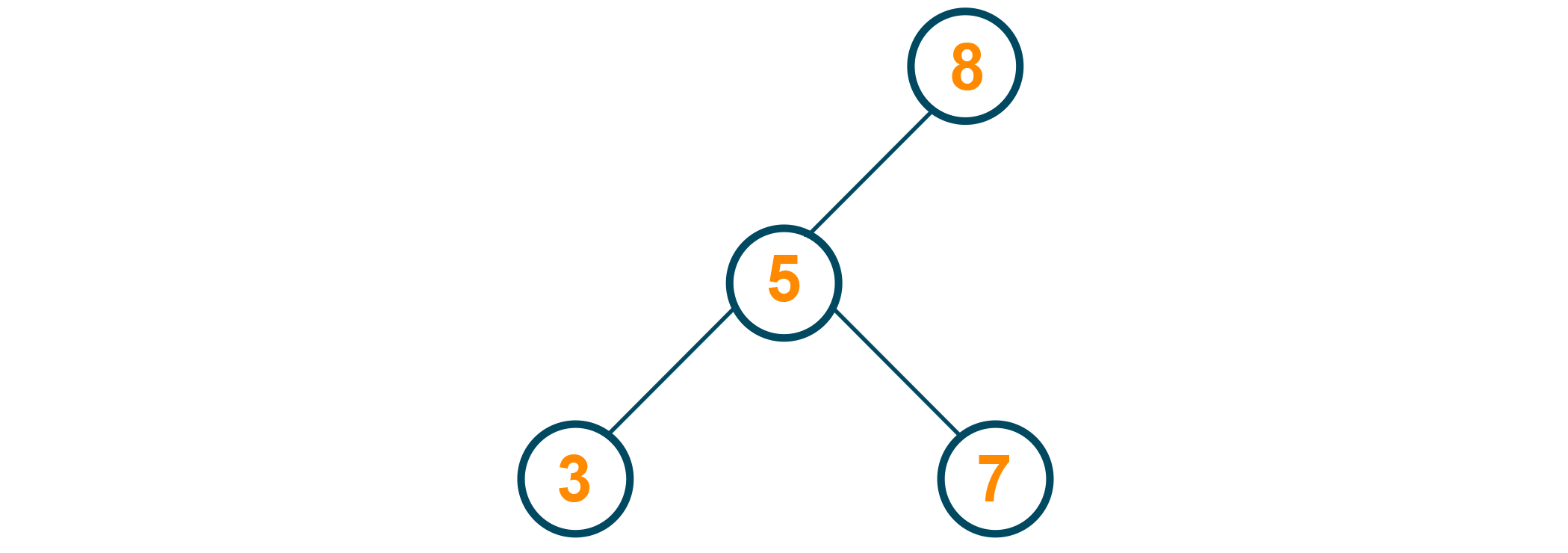
3) If the node has two children, it becomes a little tricky. We need to find the node which has the smallest value in the right subtree (among the elements that have a greater value than the node to be deleted) for the node and use that to replace the deleted node. (Note that the smallest value in the right subtree is the node that comes immediately after the node to be deleted, implying that it is the inorder successor for the node to be deleted).
Here's an example of a tree-
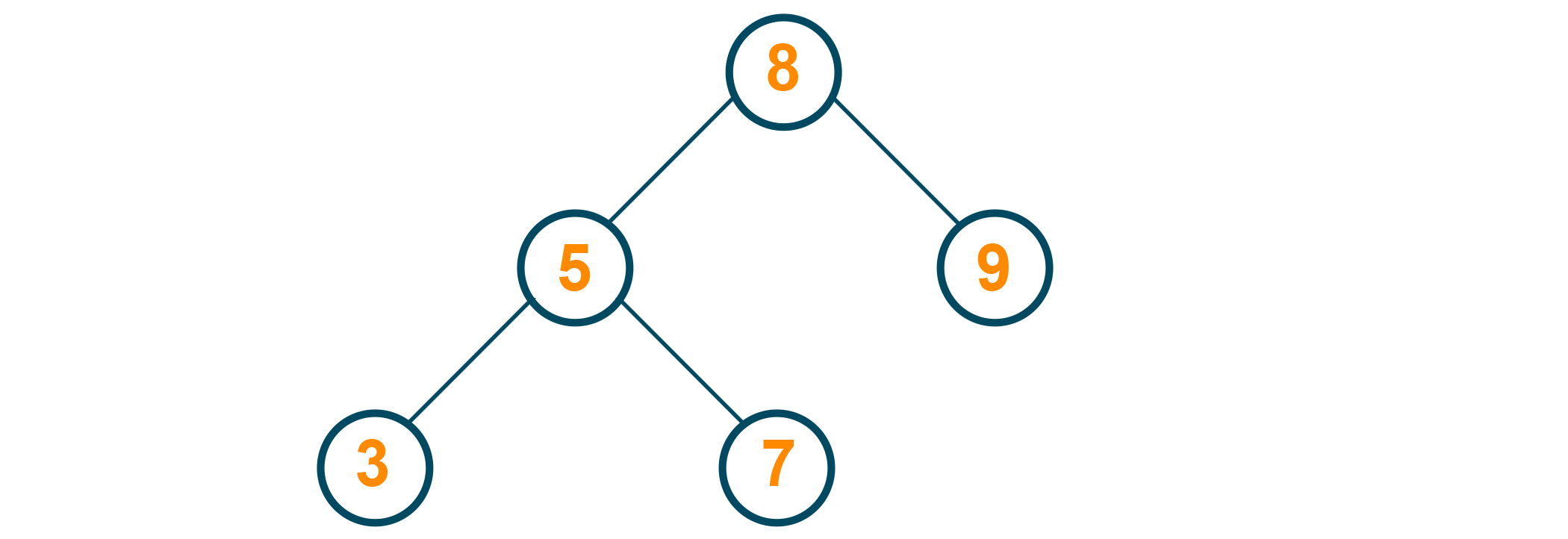
5 is to be deleted from the tree. In this case, the inorder successor of 5 (or the greatest element in the left subtree, which is 3) is to be attached to 5's predecessor (which is the root).
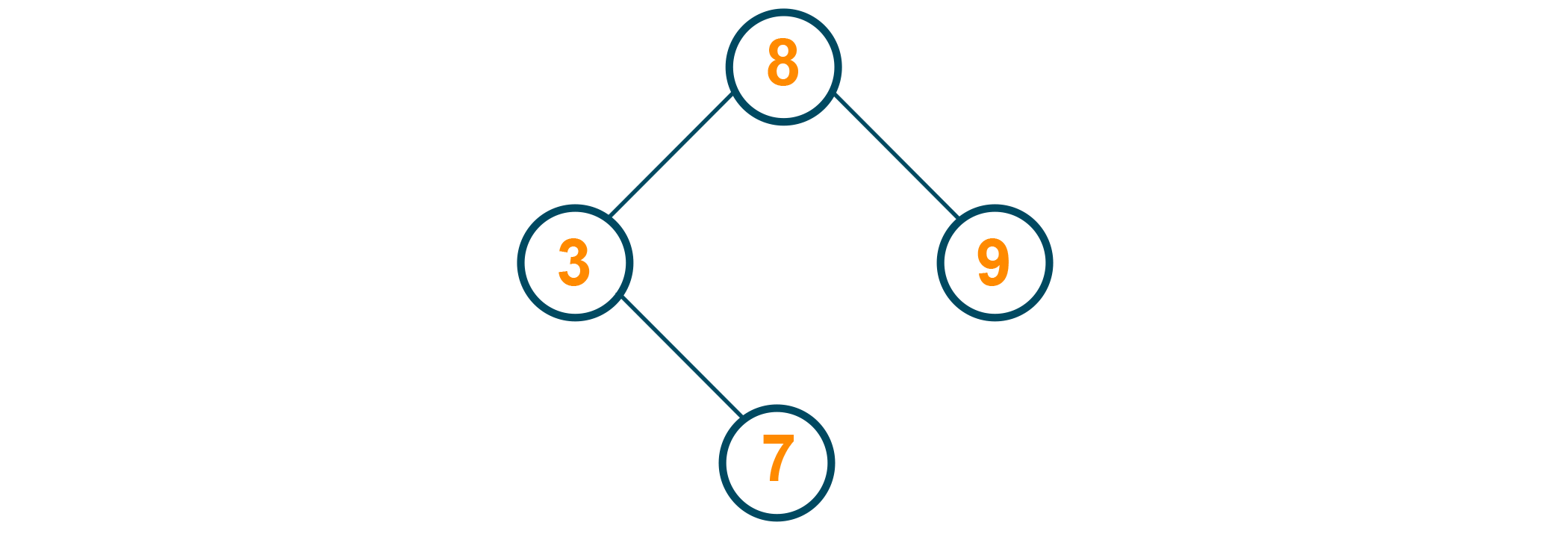
Java Program for Deletion in Binary Search Tree
public class BinarySearchTree { public static class Node { //instance variable of Node class public int data; public Node left; public Node right; //constructor public Node(int data) { this.data = data; this.left = null; this.right = null; } } // instance variable public Node root; // constructor for initialise the root to null BYDEFAULT public BinarySearchTree() { this.root = null; } // insert method to insert the new Date public void insert(int newData) { this.root = insert(root, newData); } public Node insert(Node root, int newData) { // Base Case: root is null or not if (root == null) { // Insert the new data, if root is null. root = new Node(newData); // return the current root to his sub tree return root; } // Here checking for root data is greater or equal to newData or not else if (root.data >= newData) { // if current root data is greater than the new data then now process the left sub-tree root.left = insert(root.left, newData); } else { // if current root data is less than the new data then now process the right sub-tree root.right = insert(root.right, newData); } return root; } /* * Case 1:- No child * Case 2:- 1 child * case 3:- 2 child * */ public void deleteANode(Node node) { deleteNode(this.root, node); } private Node deleteNode(Node root, Node node) { // check for node initially if (root == null) { return null; } else if (node.data < root.data) { // process the left sub tree root.left = deleteNode(root.left, node); } else if (node.data > root.data) { // process the right sub tree root.right = deleteNode(root.right, node); } else if(root.data==node.data){ // case 3: 2 child if (root.left != null && root.right != null) { int lmax = findMaxData(root.left); root.data = lmax; root.left = deleteNode(root.left, new Node(lmax)); return root; } //case 2: one child // case i-> has only left child else if (root.left != null) { return root.left; } // case ii-> has only right child else if (root.right != null) { return root.right; } //case 1:- no child else { return null; } } return root; } // inorder successor of given node public int findMaxData(Node root) { if (root.right != null) { return findMaxData(root.right); } else { return root.data; } } public void preorder(){ preorder(root); System.out.println(); } public void preorder(Node node){ if(node!=null){ System.out.print(node.data+" "); preorder(node.left); preorder(node.right); } } public static void main(String[] args) { // Creating the object of BinarySearchTree class BinarySearchTree bst = new BinarySearchTree(); // call the method insert bst.insert(8); bst.insert(5); bst.insert(9); bst.insert(3); bst.insert(7);
bst.preorder(); bst.deleteANode(new Node(9)); bst.preorder(); } }
Output :
8 5 3 7 9
8 5 3 7
Search for an Element in a Binary Search Tree
Because of the unique properties of a binary search tree, the algorithm used for searching in a binary search tree is much less complex and requires lesser time to execute. To search for an element, simply follow the below steps:-
1) If the given element is equal to the root, return the index of the root.
2) If the root is greater than the given element, move to the right subtree.
3) If the root is lesser than the given element, move to the left subtree.
4) Repeat till the element is found or till the leaves are reached. If the leaves are reached and the element still isn't found - it doesn't exist in the tree.
In the below example we are searching for element 7
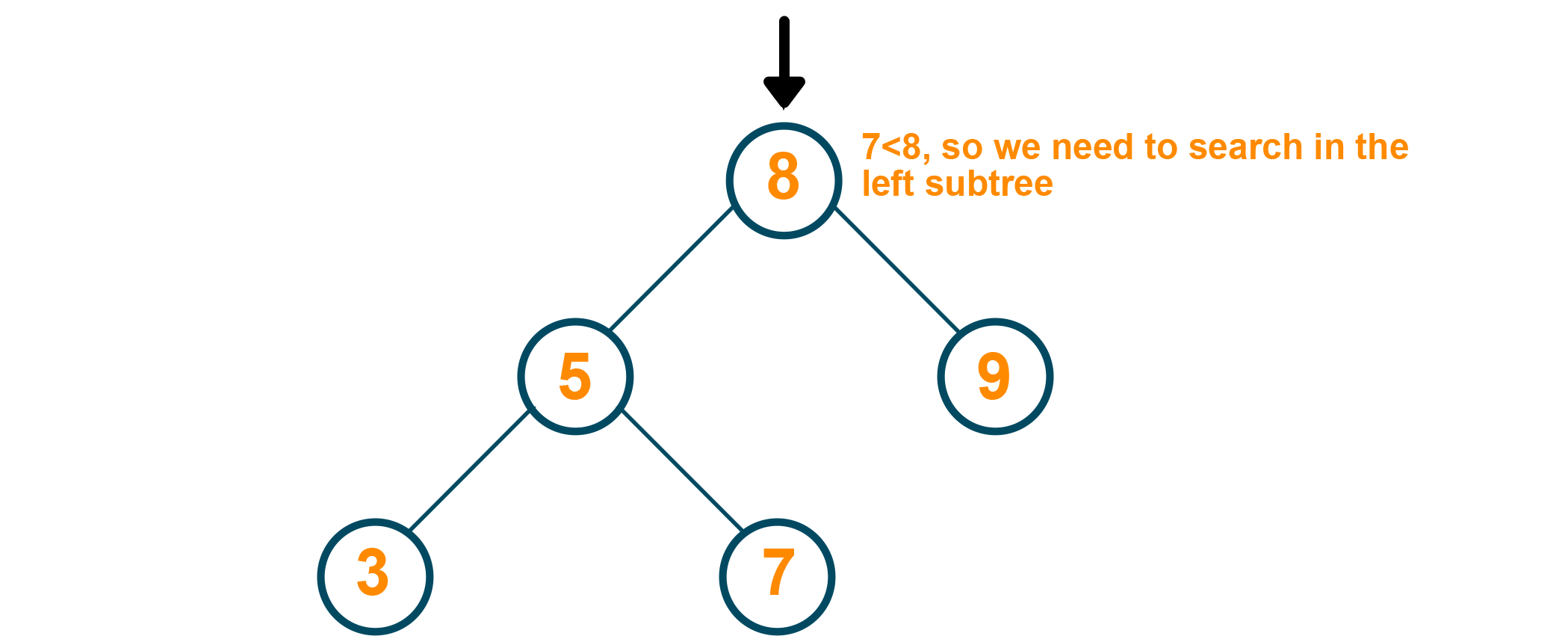
Since the root (which is 8 ) is greater than the element to be searched for, we need to search in the left subtree.
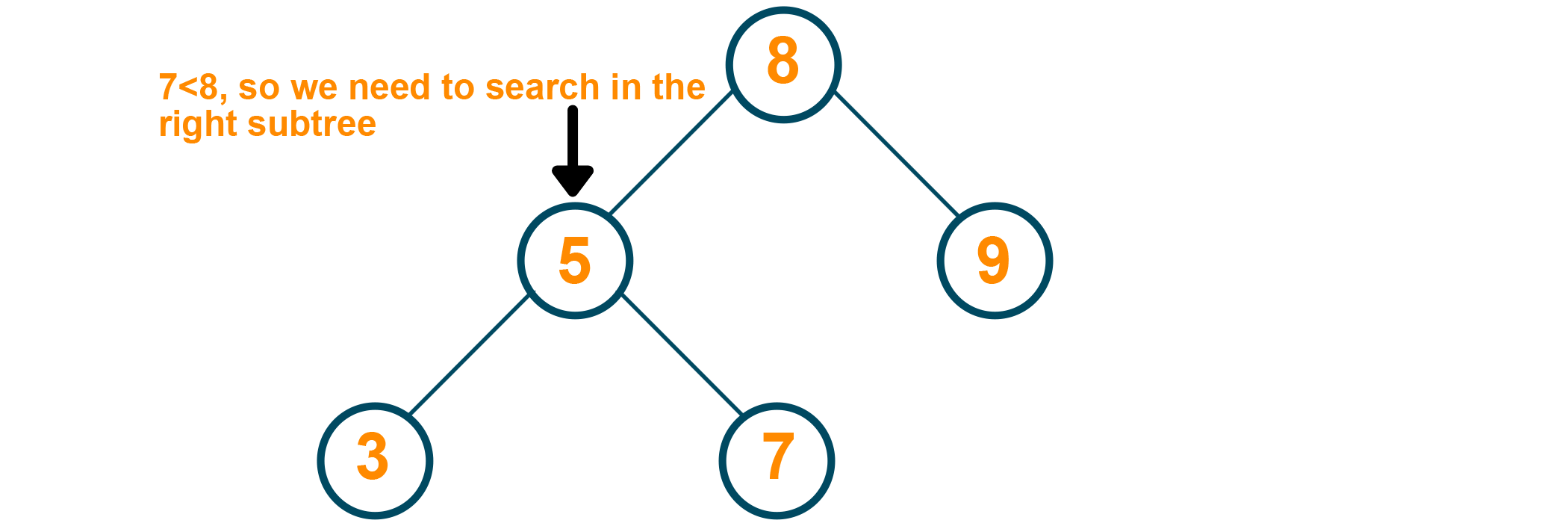
Since node 5 is of a lesser value than the element to be searched for, we need to search in the right subtree.
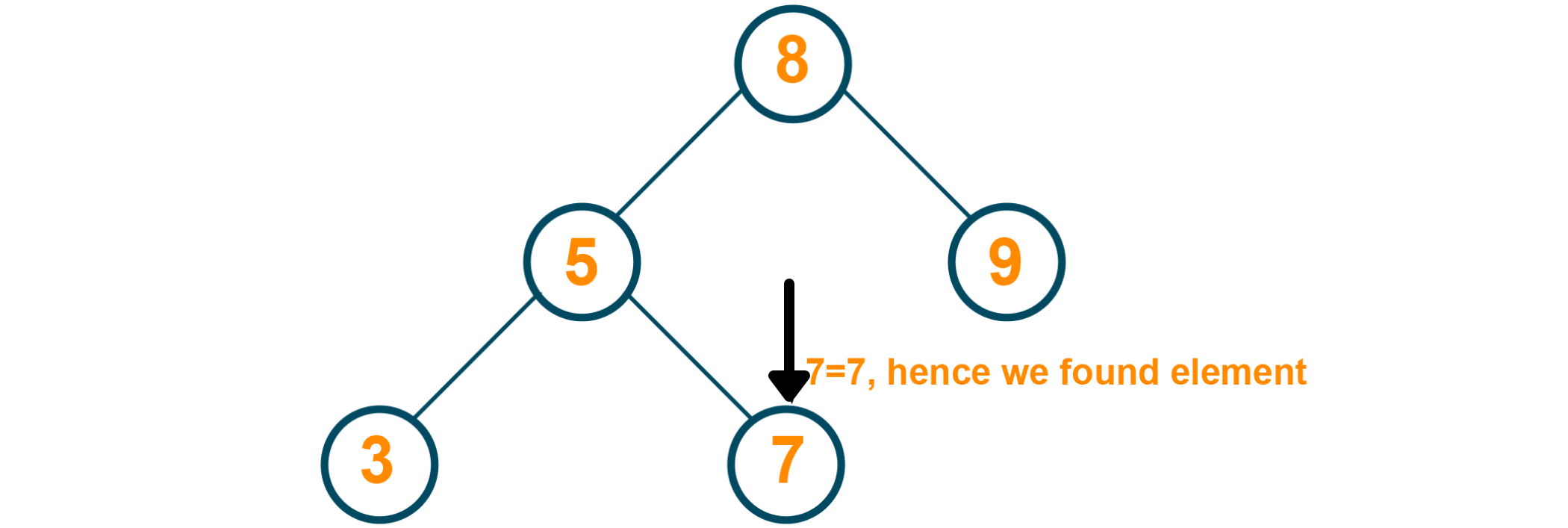
Java Program for Searching in Binary Search Tree
public class BinarySearchTree { public class Node { //instance variable of Node class public int data; public Node left; public Node right; //constructor public Node(int data) { this.data = data; this.left = null; this.right = null; } } // instance variable public Node root; // constructor for initialise the root to null BYDEFAULT public BinarySearchTree() { this.root = null; } // insert method to insert the new Date public void insert(int newData) { this.root = insert(root, newData); } public Node insert(Node root, int newData) { // Base Case: root is null or not if (root == null) { // Insert the new data, if root is null. root = new Node(newData); // return the current root to his sub tree return root; } // Here checking for root data is greater or equal to newData or not else if (root.data >= newData) { // if current root data is greater than the new data then now process the left sub-tree root.left = insert(root.left, newData); } else { // if current root data is less than the new data then now process the right sub-tree root.right = insert(root.right, newData); } return root; } // method for search the data , is data is present or not in the tree ? public boolean search(int data) { return search(this.root, data); } private boolean search(Node root, int data) { if (root == null) { return false; } else if (root.data == data) { return true; } else if (root.data > data) { return search(root.left, data); } return search(root.right, data); } //Traversal public void preorder() { preorder(root); System.out.println(); } public void preorder(Node root) { if (root == null) { return; } System.out.print(root.data + " "); preorder(root.left); preorder(root.right); } public static void main(String[] args) { // Creating the object of BinarySearchTree class BinarySearchTree bst = new BinarySearchTree(); // call the method insert bst.insert(8); bst.insert(5); bst.insert(9); bst.insert(3); bst.insert(7); bst.preorder(); System.out.println(bst.search(7)); } }
Output :
8 5 3 7 9
true
Find Maximum Element in a Binary Search Tree
The unique properties of a binary search tree make it very easy to find the maximum or minimum elements in the tree. In a binary tree, it becomes necessary to scour the entire tree for finding the maximum or minimum, which increases the time complexity of the algorithm. Since the elements greater than the root are always stored in the right subtree, one intelligent guess would be to check the right subtree continuously till the rightmost element (or more appropriately, rightmost leaf) is found. That is the greatest element in the binary search tree.
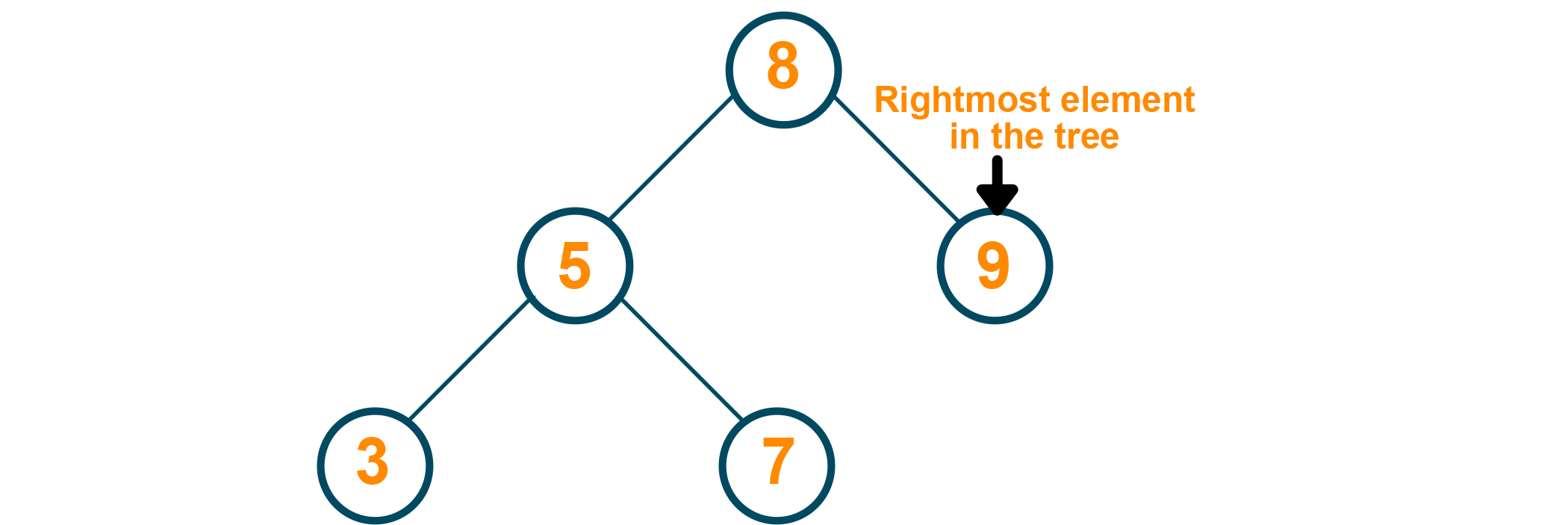
Java Program for Maximum Element in Binary Search Tree
public class BinarySearchTree { public class Node { //instance variable of Node class public int data; public Node left; public Node right; //constructor public Node(int data) { this.data = data; this.left = null; this.right = null; } } // instance variable public Node root; // constructor for initialise the root to null BYDEFAULT public BinarySearchTree() { this.root = null; } // insert method to insert the new Date public void insert(int newData) { this.root = insert(root, newData); } public Node insert(Node root, int newData) { // Base Case: root is null or not if (root == null) { // Insert the new data, if root is null. root = new Node(newData); // return the current root to his sub tree return root; } // Here checking for root data is greater or equal to newData or not else if (root.data >= newData) { // if current root data is greater than the new data then now process the left sub-tree root.left = insert(root.left, newData); } else { // if current root data is less than the new data then now process the right sub-tree root.right = insert(root.right, newData); } return root; } // method to get maximum value in the binary search tree // we are assured the maximum value is present is in root data if root is null otherwise // it is in right subtree of the binary search tree public int findMaximum() { if(root==null){ return -1; } // processing the right sub tree Node current = this.root; while (current.right != null) { current = current.right; } return (current.data); } public static void main(String[] args) { // Creating the object of BinarySearchTree class BinarySearchTree bst = new BinarySearchTree(); // call the method insert bst.insert(8); bst.insert(5); bst.insert(3); bst.insert(7); bst.insert(9); System.out.println(bst.findMaximum()); } }
Output:
9
Find Minimum Element in a Binary Search Tree
The arrangement of nodes in a binary search tree makes it algorithmically less complex to reach the minimum or maximum element in a tree. All elements lesser than the root are stored in the left subtree, so the approach would be to keep proceeding left along the binary search tree till the leftmost element is found. More appropriately, we are looking for the leftmost leaf in the tree.
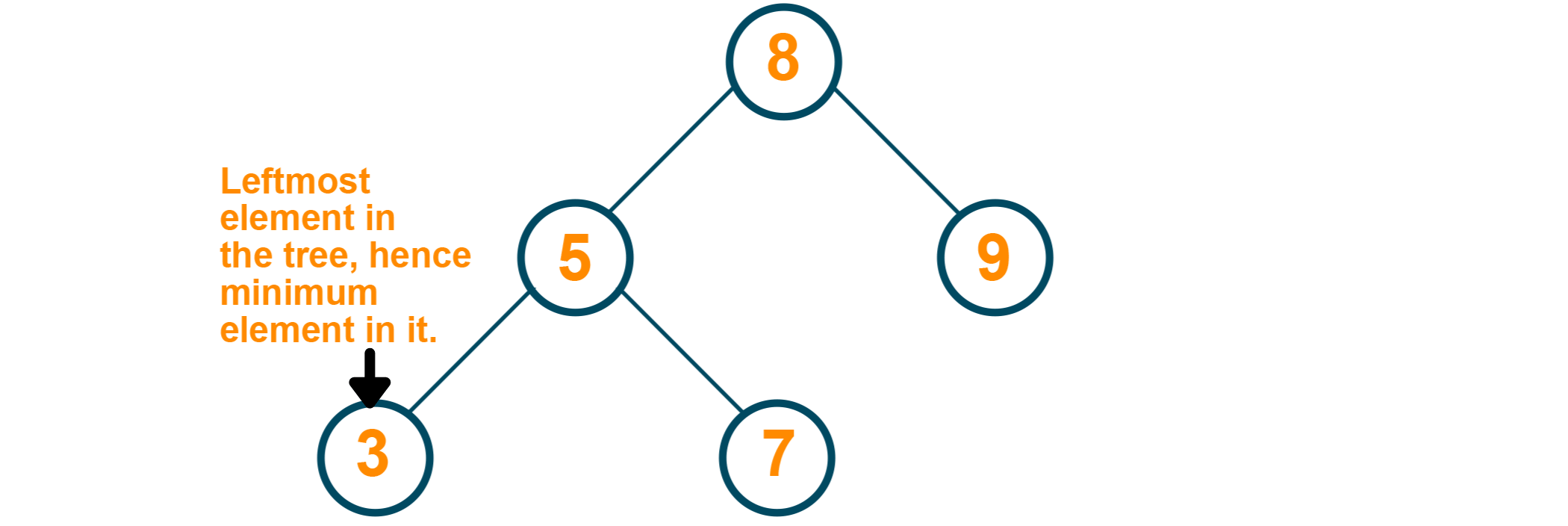
Java Program for Minimum Element in Binary Search Tree
public class BinarySearchTree { public class Node { //instance variable of Node class public int data; public Node left; public Node right; //constructor public Node(int data) { this.data = data; this.left = null; this.right = null; } } // instance variable public Node root; // constructor for initialise the root to null BYDEFAULT public BinarySearchTree() { this.root = null; } // insert method to insert the new Date public void insert(int newData) { this.root = insert(root, newData); } public Node insert(Node root, int newData) { // Base Case: root is null or not if (root == null) { // Insert the new data, if root is null. root = new Node(newData); // return the current root to his sub tree return root; } // Here checking for root data is greater or equal to newData or not else if (root.data >= newData) { // if current root data is greater than the new data then now process the left sub-tree root.left = insert(root.left, newData); } else { // if current root data is less than the new data then now process the right sub-tree root.right = insert(root.right, newData); } return root; } // method to get minimum value in the binary search tree // we are assured the minimum value is present is in root data if root is null otherwise // it is in left subtree of the binary search tree public int findMinimum() { if(root==null){ return -1; } // processing the left sub tree Node current = this.root; while (current.left != null) { current = current.left; } return (current.data); } public static void main(String[] args) { // Creating the object of BinarySearchTree class BinarySearchTree bst = new BinarySearchTree(); // call the method insert bst.insert(8); bst.insert(5); bst.insert(3); bst.insert(7); bst.insert(9); System.out.println(bst.findMinimum()); } }
Output:
3
Time Complexity of the Operations on a Binary Search Tree
The time complexity of the various operations in a binary search tree can be summarised using the table below:-
| Operation | Time Complexity | Space Complexity |
| Searching for an element | O(h), where h is the height of the tree. O(n) in the worst case. | O(1) |
| Insertion of an element | O(h), where h is the height of the tree. O(n) in the worst case. | O(1) |
| Deletion of an element | O(h), where h is the height of the tree. O(n) in the worst case. | O(1) |
| Finding the maximum element | O(h), where h is the height of the tree. O(n) in the worst case. | O(1) |
| Finding the minimum element | O(h), where h is the height of the tree. O(n) in the worst case. | O(1) |
Thus, a binary search tree maintains a unique homogeneity in all of its operations. While there aren't major gains in case of insertion or deletion of an element (since the conditions for a binary search tree always have to be satisfied), searching becomes much faster. It is also easier to find the maximum element or the minimum element in a binary search tree. There is a chance that the time complexity is increased, which happens in the case of a skewed tree (a tree where all elements occur in one subtree). However, for the most part, there is an increase in the searching speed if we are using a binary search tree, making it very useful for solving certain types of problems.
Drawbacks of a BST
The heading might sound slightly misleading since a binary search tree improves the fundamental design of a binary tree in many ways. A binary search tree was built to bridge the gap between arrays and trees, making the operations on a binary search tree slightly slower than the ones on an array. The main problem happens if a binary search tree does not have any regulatory mechanism for maintaining its height. With no such check in place, the tree may grow unabated in one direction - making it skewed by nature and increasing the time complexity of all operations being performed on it.
When regulatory mechanisms are put in place to keep the height of the tree in check, we obtain a special variant of the binary search tree called a self-balancing binary search tree.
Two main examples of self-balancing binary search trees include AVL trees and red-black trees. Both AVL trees and red-black trees have extensive uses in the solution of algorithmic problems.
Applications of Binary Search Tree
A binary search tree has many applications in real life:-
- Binary search trees are used when deletion and insertion of data from a dataset are very frequent. The unique homogeneity in the time complexities of the various operations of the binary search tree allows this to be done faster.
- Binary search trees form an essential part of search algorithms. These algorithms are used in many functions we use in our day-to-day lives, like map, filter, reduce, and so on.
- A special form of the binary search tree, called a self-balancing binary search tree, has many applications like maintaining a sorted stream of data. Self-balancing trees are also used if it is necessary to be able to extract the minimum element or the maximum element.
- Expression trees are a special form of binary search trees under the hood that is used for the evaluation of arithmetic and logical expressions.
- Virtual memory distribution and management are done by kernels with the help of binary search trees.
Also, check this article on how to validate binary search tree.
Conclusion
A binary search tree (BST) is a very useful data structure that is useful for doing a lot of work like searching, insertion, and deletion in lesser time. This article on the various operations on a binary search tree along with their codes in java should be enough to bring you to pace with the basics of the data structure and its practical uses. For more details, please refer to our extensive tutor program designed by experts (which should help you learn a lot more than just the basics!).
