A binary tree is a unique data structure adopted for data storage schemes in the field of computer science. It has the benefits of both an ordered array and a linked list, therefore, the time complexity for search is as fast as in a sorted array, and insertion/deletion operations are as swift as in a linked list. In this article, we will learn how to find the height of a binary tree in Python with code.
But before moving on, we must revise some basic concepts of binary trees.
What is a Binary Tree?
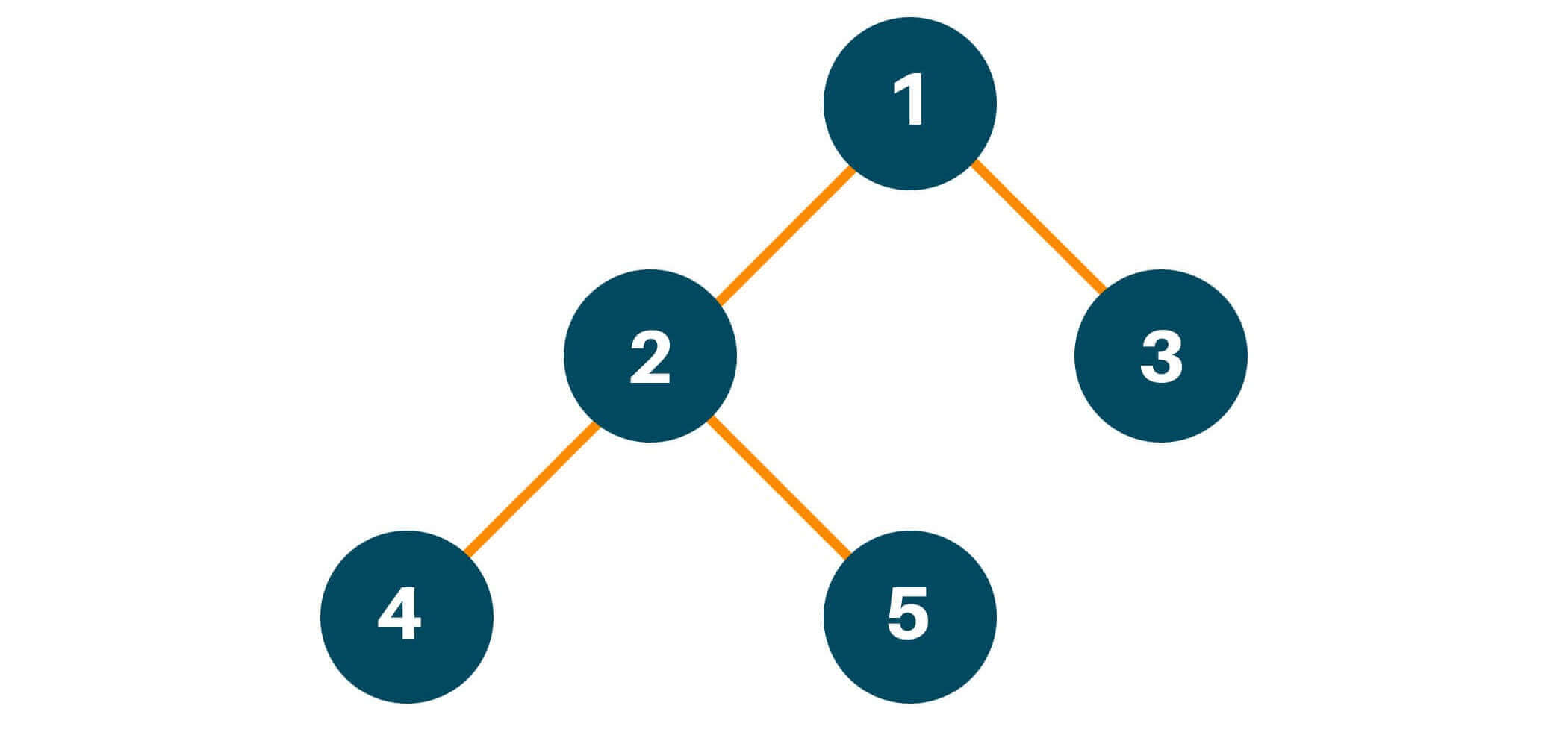
In computer science, a binary tree is a hierarchical data structure made up of nodes. Each node has no more than two children, referred to as the left and right children. The root is the initial node in a binary tree, and all other nodes are either the root's left or right children or their descendants.
Note that the binary tree is an ordered tree, with each node's location defined by the structure of its parent and children. In computer science, binary trees are frequently used to represent hierarchical data, such as file systems and syntax trees for programming languages.
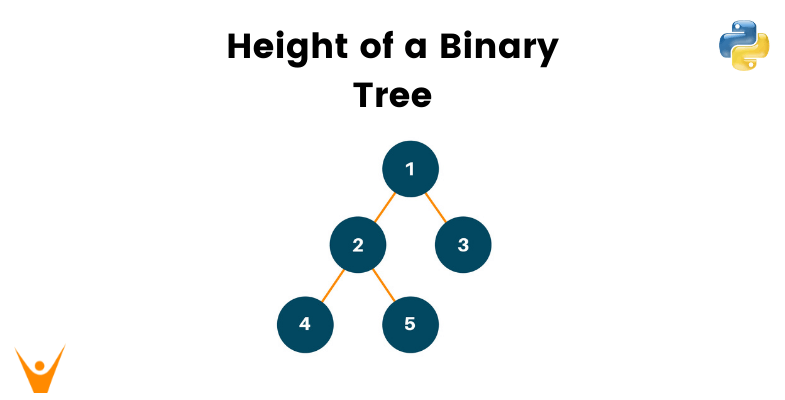
Here is an example for you to better understand:
What is the Height of a Binary Tree?
A binary tree's height is the number of edges that can be traveled from the root node to any leaf node. It's also known as the depth of the binary tree. The number of nodes in the tree is used to calculate the height of a binary tree.
Let h be the height of a binary tree and n be its number of nodes. The height of the binary tree is calculated as h = log2(n+1) - 1. This formula requires that the binary tree is a full binary tree, which means that all levels are entirely filled, except the last level, which is filled from left to right.
Consider a binary tree with a single node with a height of 0. This will help you comprehend the formula. h = log2(1+1) - 1 = 0 is the formula. Consider a binary tree with three nodes and a height of one. h = log2(3+1) - 1 = 1 is the formula. Similarly, a binary tree with seven nodes is two nodes tall, a binary tree with fifteen nodes is three nodes tall, and so on.
Assuming that the binary tree is complete, the formula sets an upper constraint on its height. If the binary tree is not full, the height may be less than the formula's upper bound.
How to find the Height of a Binary Tree?
As we studied before. the height of the binary tree is considered to be the longest path starting from the root node to any leaf node in the binary tree. If the target node for which we have to calculate the height, doesn’t have any other nodes connected to it, conclusively the height of that node would be 0.
Therefore, we can say that the height of a binary tree is the elevation from the root node in the entire binary tree. In layman's terms, the height of a binary tree is equivalent to the largest quantity of edges starting from the root to the most sparse leaf node in the binary tree.
A related concept in the binary tree data structure is the depth of the tree. According to the definition of depth of a node in the binary tree is the total amount of edges starting from the root node to the destination node.
The figure below shows a binary tree with 4 levels indicated.
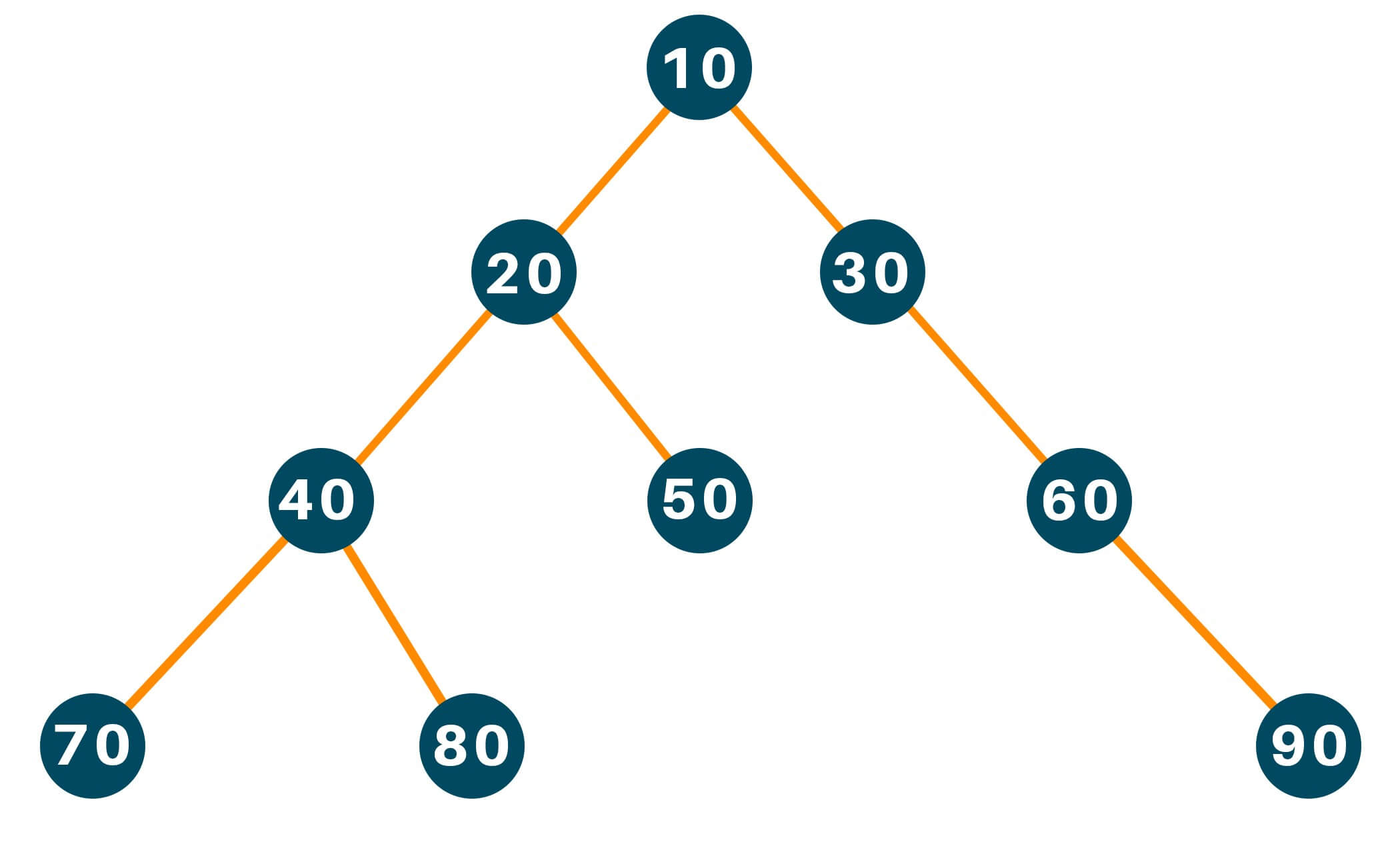
The leaf nodes of the binary tree are : [70, 80, 50, 90]
For the leaf node 70, the number of nodes along the edges is 4.
For the leaf node 80, the number of nodes along the edges is 4.
For the leaf node 50, the number of nodes along the edges is 3.
For the leaf node 90, the number of nodes along the edges is 4.
The maximum number of nodes from root to farthest leaf is: max(4, 4, 3, 4) is 4. Hence, the height of the binary tree is 4.
There are two methods to approach this problem statement. The first Approach is based on the Depth-first search using recursion, and the other method is based on the Breadth-first search using Level order traversal without using recursion.
Finding The Height With Recursion (Depth First search)
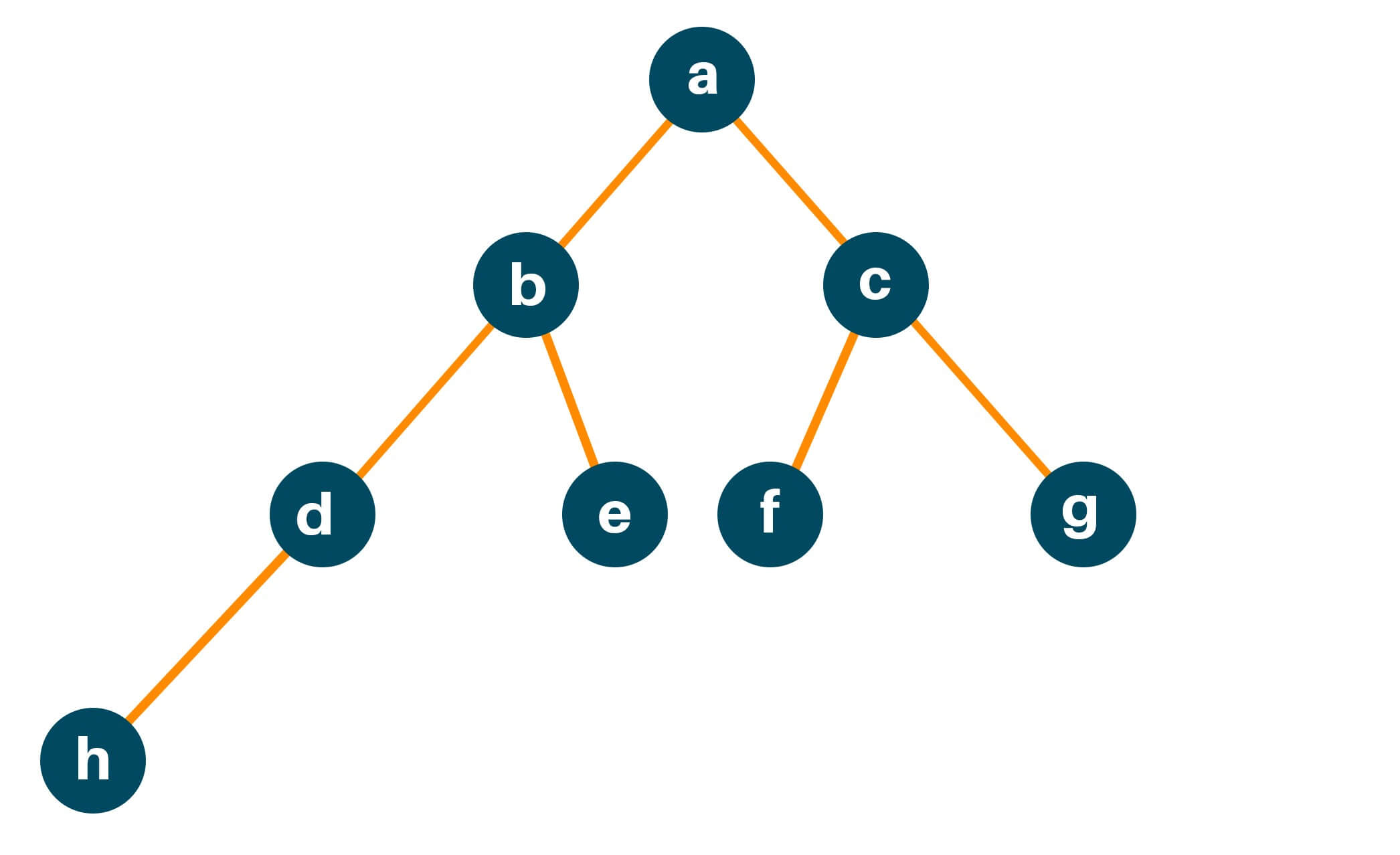
Let us consider an example to understand the approach in an easier way. Consider the following Binary Tree, with ‘a’ as the root node and ‘h’, ‘e’, ‘f’ and ‘g’ as the leaf node:
For the leaf node ‘h’, the number of nodes along the edges is 4.
For the leaf node ‘e’, the number of nodes along the edges is 3.
For the leaf node ‘f’, the number of nodes along the edges is 3.
For the leaf node ‘g’, the number of nodes along the edges is 3.
The maximum number of nodes from root to farthest leaf is: max(4, 3, 3, 3) 4. Hence, the height of the binary tree is 4.
Let us discuss the step-by-step implementation.
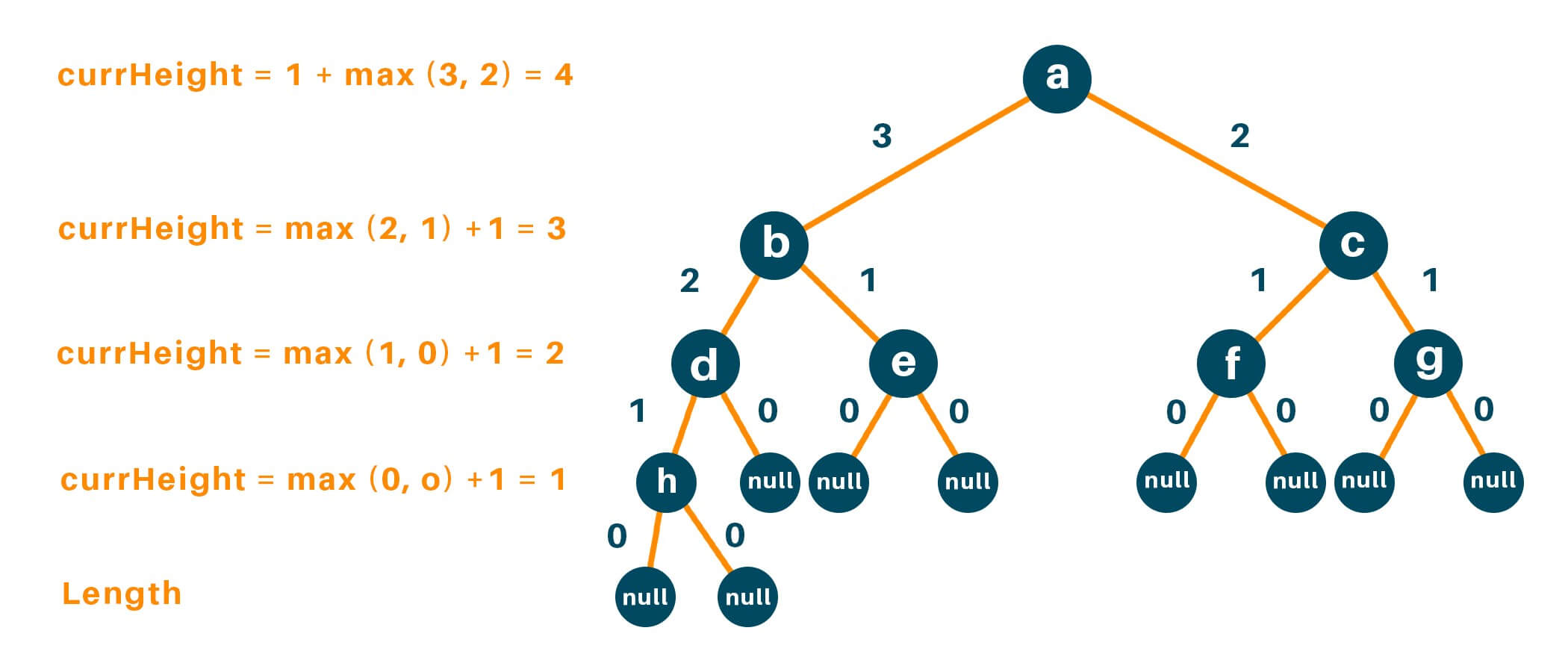
Step 1: Ask the root node, what is the height of the binary tree if the root node is ‘a’, and recursively the root node asks the same question to its left which is ‘b’, and the right child which is ‘c’. And so on.
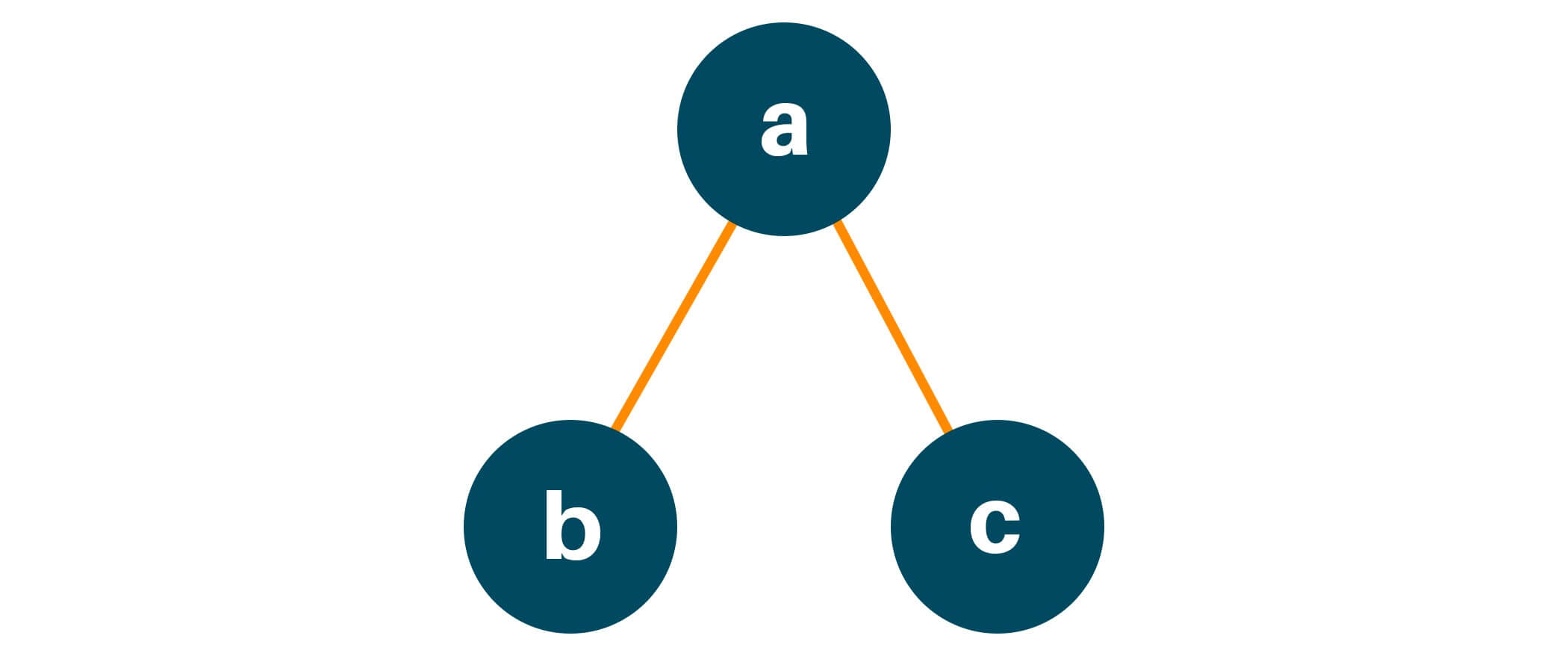
Step 2: Recursively ‘b’ will do the same as the node ‘a’ and ask its left child ‘d’ and the right child ‘e’ what will be the height if you are the root node of the current binary tree, ie.
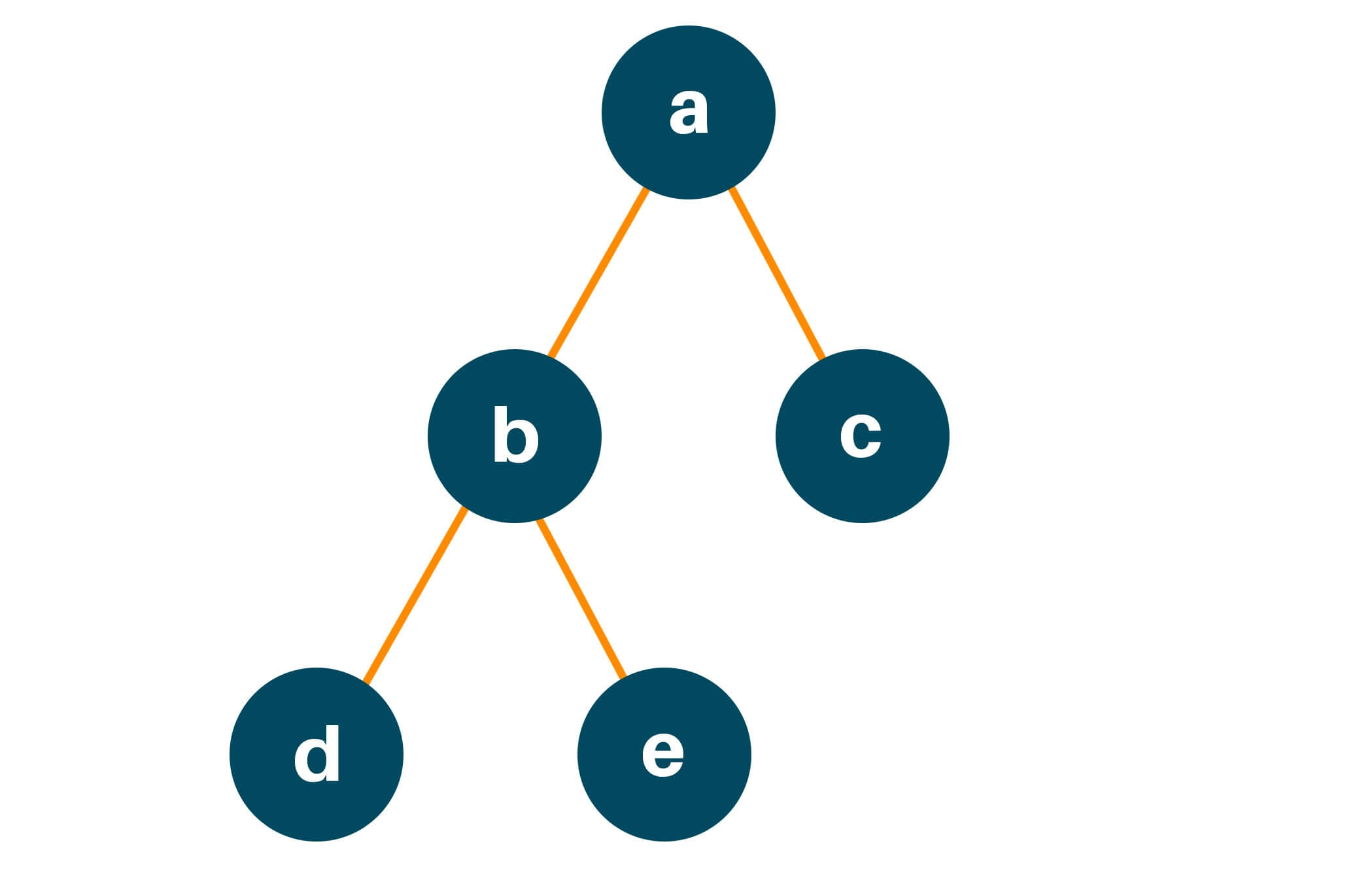
Step 3: The node ‘d’ asks the same questions to its left and right child ie.
The node ‘h’ does the same thing and now since the left node of ‘h’ is NULL it returns 0.
Step 4: The node ‘h’ gives out the result of its left and right child, and after we find the maximum length between the leftHeight and rightHeight, where :
leftHeight = 0
rightHeight = 0
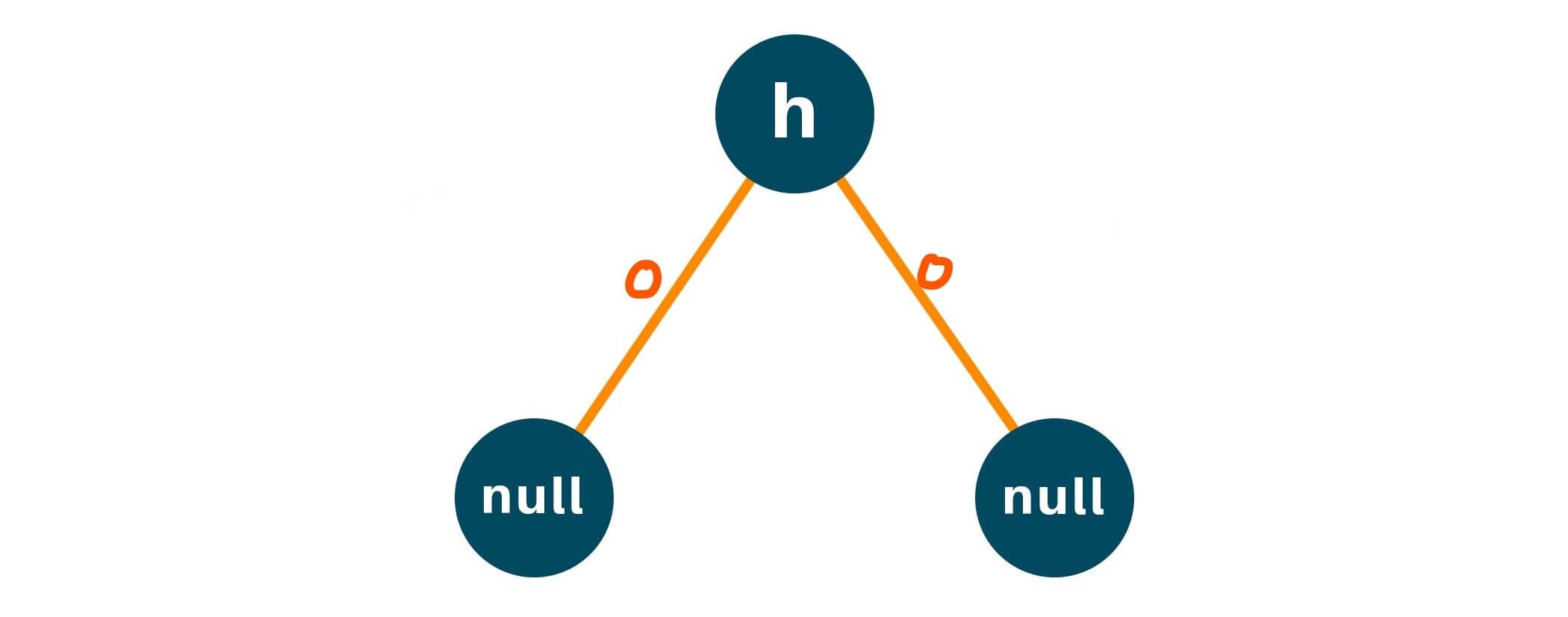
max(0, 0) = 0
Therefore, at each iteration the node will return length: 1 + max(leftHeight, rightHeight)
Step 5: To get a better intuition of the algorithm, refer to the following image:
Here is the Python code to find the height of a binary tree with recursion:
# define a Class Tree, to intiate the binary tree class TreeNode: def __init__(self, val): self.val = val self.left = None self.right = None def height(root): # Check if the binary tree is empty if root is None: # If TRUE return 0 return 0 # Recursively call height of each node leftAns = height(root.left) rightAns = height(root.right) # Return max(leftHeight, rightHeight) at each iteration return max(leftAns, rightAns) + 1 # Test the algorithm root = TreeNode(1) root.left = TreeNode(2) root.right = TreeNode(3) root.left.left = TreeNode(4) print("Height of the binary tree is: " + str(height(root)))
Output:
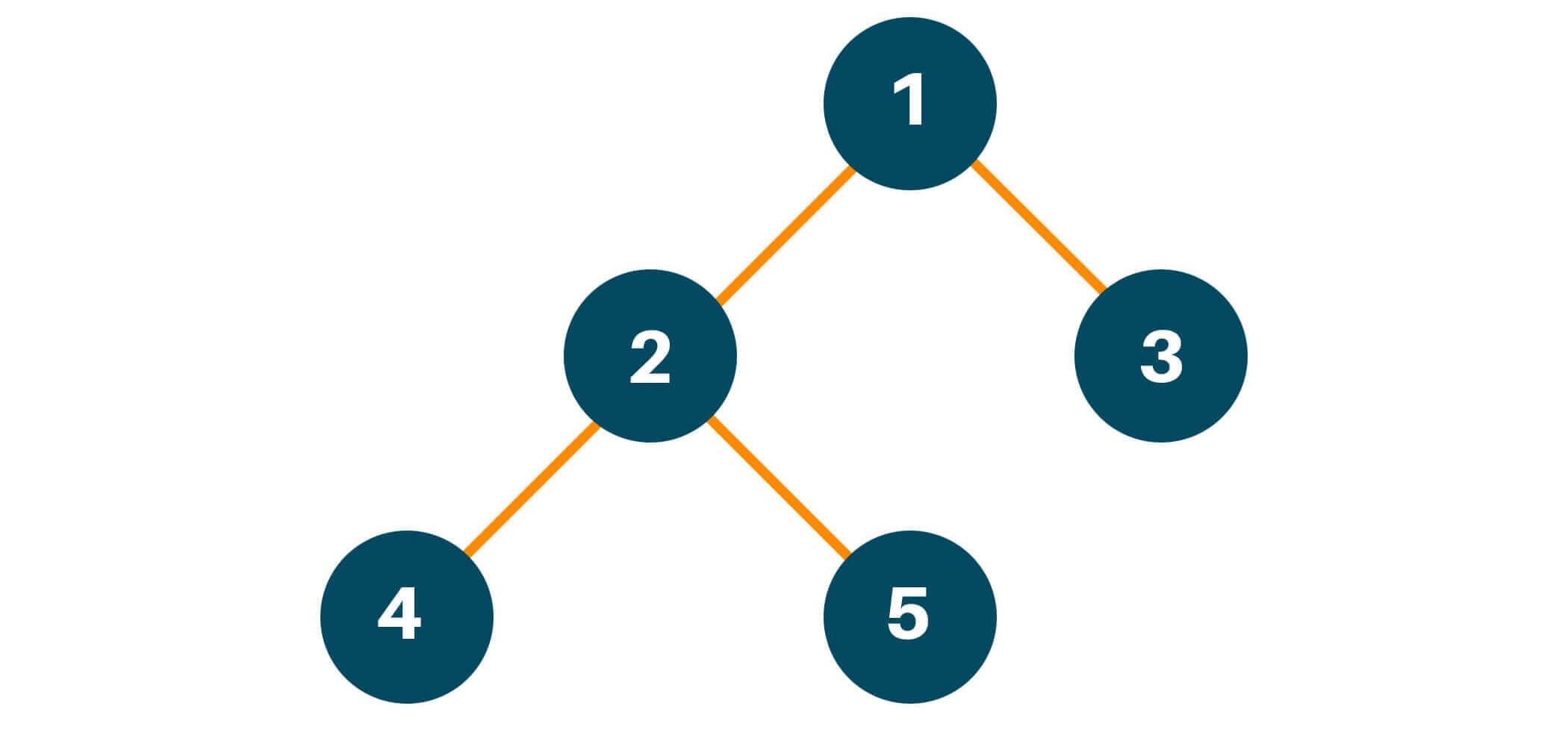
Height of the binary tree is: 3
The time complexity of the algorithm is O(n) as we iterate through node of the binary tree calculating the height of the binary tree only once.nd the space complexity is also O(n) as we are following recursion, where recursive stack can have upto n elements. Here n is the number of nodes in the binary tree.
Finding the Height Without Recursion (Breadth-First search)
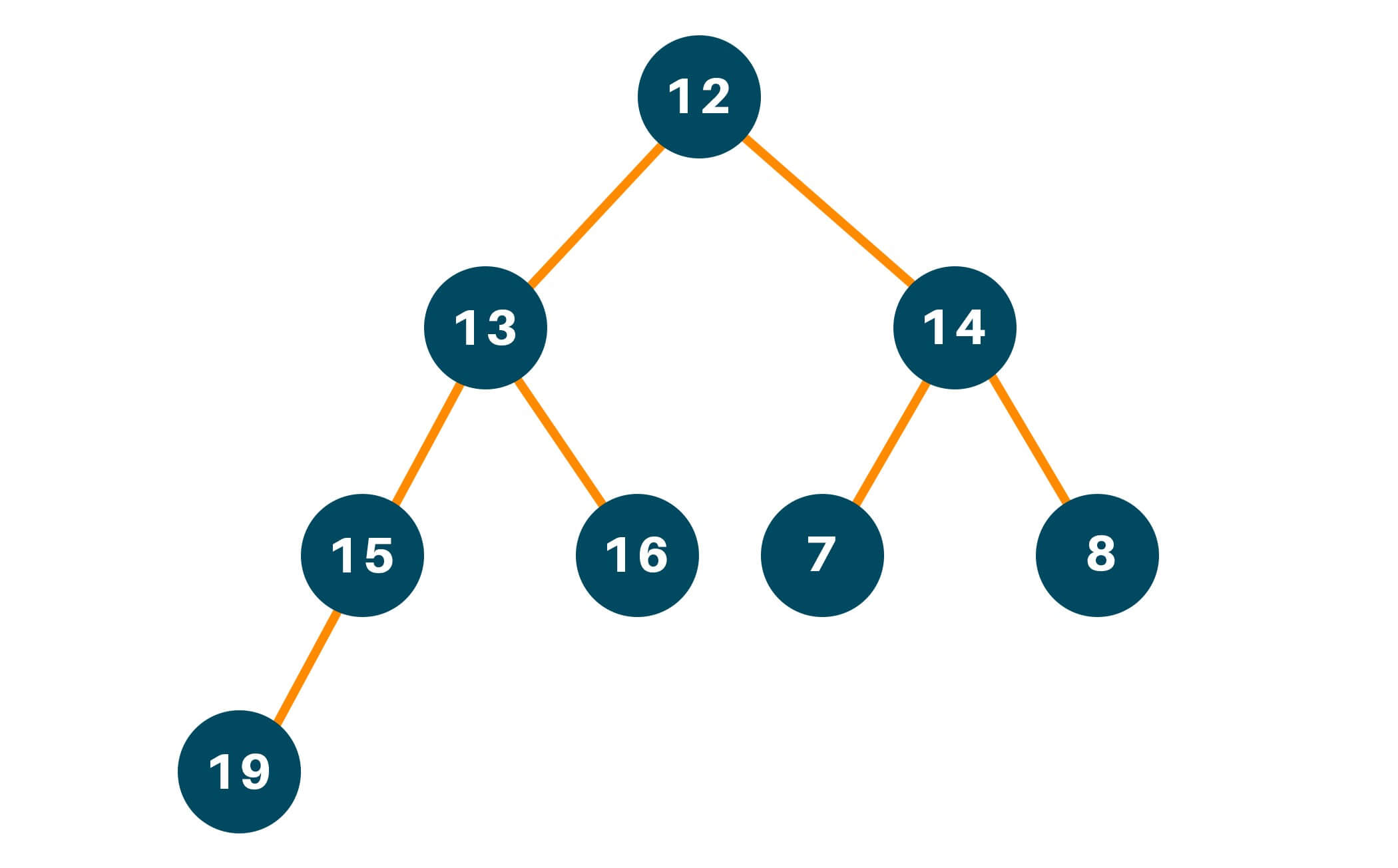
Let us consider an example to understand the approach in an easier way. Consider the following Binary Tree, with 12 as the root node and 19, 16, 7, and 8 as the leaf node:
For the leaf node 19, the number of nodes along the edges is 4.
For the leaf node 16, the number of nodes along the edges is 3.
For the leaf node 7, the number of nodes along the edges is 3.
For the leaf node 8, the number of nodes along the edges is 3.
The maximum number of nodes from root to farthest leaf is: max(4, 3, 3, 3) is 4. Hence, the height of the binary tree is 4.
Let us discuss the step-by-step implementation :
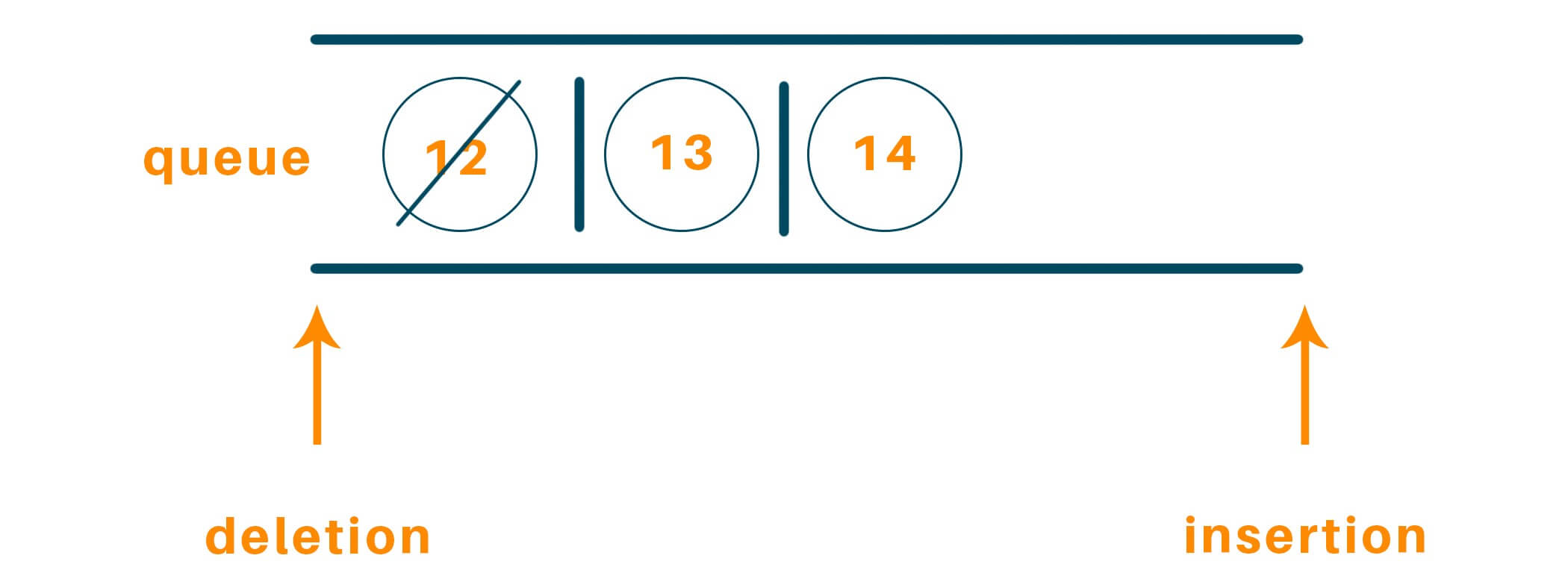
Step 1: Use a queue data structure to approach this problem statement, hence, initialize an empty queue data structure.

Set ‘ans’ variable to 0.
ans = 0
Step 2: Enqueue root node to the queue and process it in a while loop until there are no elements left and perform the same process for the other nodes, ie.
Enqueue root node 12

currSize = 1
Step 3: Run a while loop until currSize = 0, and till then keep dequeuing elements and after processing the elements when the value of currSize = 0, increment the value of ans
Therefore, dequeue 12, and check for its left child which is 13 and the right child which is 14, and enqueue them
Now:
currSize = 0
currNode = 12
Since, currSize = 0
ans = 1
At the next iteration currSize = 2
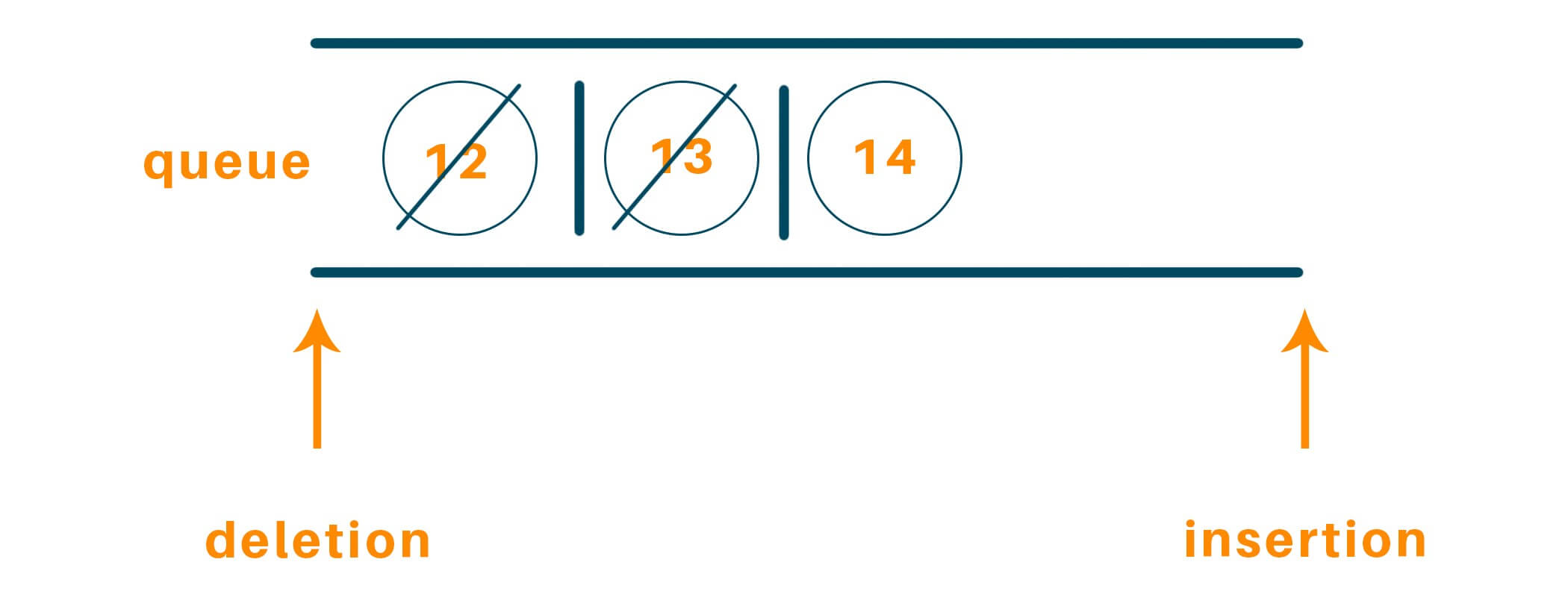
Dequeue 13 and repeat steps 2 and 3
Now:
currSize = 1
currNode = 13
Again, dequeue 14 and repeat steps 2 and 3
Now:
currSize = 0
currNode = 14
Since, currSize = 0
ans = 2

Follow, the steps repeatedly until there are no nodes to enqueue into the queue, after all the steps
ans = 4

Therefore, we receive ans = 4, the ie height of the binary tree is 4.
Here is the Python code to find the height of a binary tree without recursion:
# Import Collections libaray to use Queue Datastructure import collections # define a Class Tree, to intiate the binary tree class TreeNode: def __init__(self, val): self.val = val self.left = None self.right = None def height(root): # Set result variable to 0 ans = 0 # Initialise the queue queue = collections.deque() # Check if the tree has no nodes if root is None: return ans # Append the nodes to queue and process it in while loop until its empty queue.append(root) # Process in while loop until there are elements in queue while queue: currSize = len(queue) # Unless the queue is empty while currSize > 0: # Pop elements one-by-one currNode = queue.popleft() currSize -= 1 # Check if the node has left/right child if currNode.left is not None: queue.append(currNode.left) if currNode.right is not None: queue.append(currNode.right) # Increment ans when currSize = 0 ans += 1 return ans # Test the algorithm root = TreeNode(1) root.left = TreeNode(2) root.right = TreeNode(3) root.left.left = TreeNode(4) print("Height of the binary tree is: " + str(height(root)))
Output:
Height of the binary tree is: 3
The time complexity of the algorithm is O(n) as we iterate through nodes of the binary tree calculating the height of the binary tree only once. And the space complexity is also O(n) as we are using extra space for the queue. Here n is the number of nodes in the binary tree.
Conclusion
In this tutorial, we learned how to find the height of a binary tree with implementation in Python programming. First, we applied a recursive approach using depth-first search, and in the second approach, we apply breadth-first search without recursion using a queue data structure. Happy Learning :)