Heap in Python | Min Heap and Max Heap Implementation

In this article, we will learn what a heap is in python and its implementation. We will understand max heap and min heap concepts with their python program implementation and the difference between max-heap and min-heap. Lastly, we will learn the time complexity and applications of heap data structure. So, let's get started!

What is Heap?

Heap is a data structure that follows a complete binary tree's property and satisfies the heap property. Therefore, it is also known as a binary heap. As we all know, the complete binary tree is a tree with every level filled and all the nodes are as far left as possible. In the binary tree, it is possible that the last level is empty and not filled. Now, you must be wondering what is the heap property? In the heap data structure, we assign key-value or weight to every node of the tree. Now, the root node key value is compared with the children’s nodes and then the tree is arranged accordingly into two categories i.e., max-heap and min-heap. Heap data structure is basically used as a heapsort algorithm to sort the elements in an array or a list. Heapsort algorithms can be used in priority queues, order statistics, Prim's algorithm or Dijkstra's algorithm, etc. In short, the heap data structure is used when it is important to repeatedly remove the objects with the highest or the lowest priority.

As learned earlier, there are two categories of heap data structure i.e. max-heap and min-heap. Let us understand them below but before that, we will study the heapify property to understand max-heap and min-heap. 

What is Heapify?

Before moving forward with any concept, we need to learn what is heapify. So, the process of creating a heap data structure using the binary tree is called Heapify. The heapify process is used to create the Max-Heap or the Min-Heap. Let us study the Heapify using an example below:

Consider the input array as shown in the figure below:

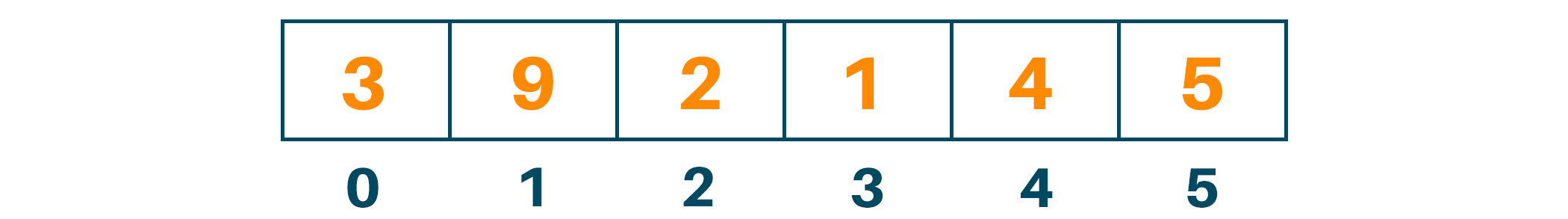
Using this array, we will create the complete binary tree

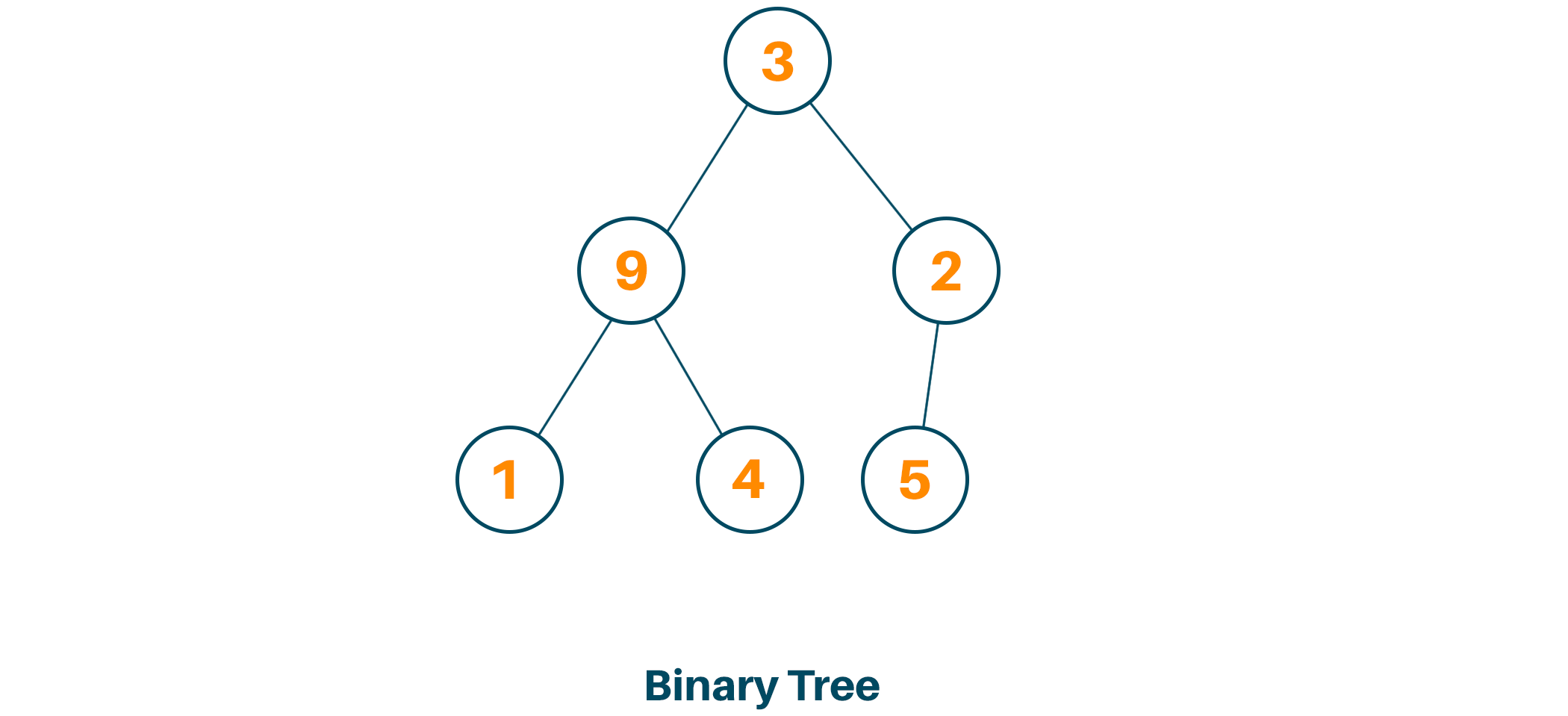
We will start the process of heapify from the first index of the non-leaf node as shown below:

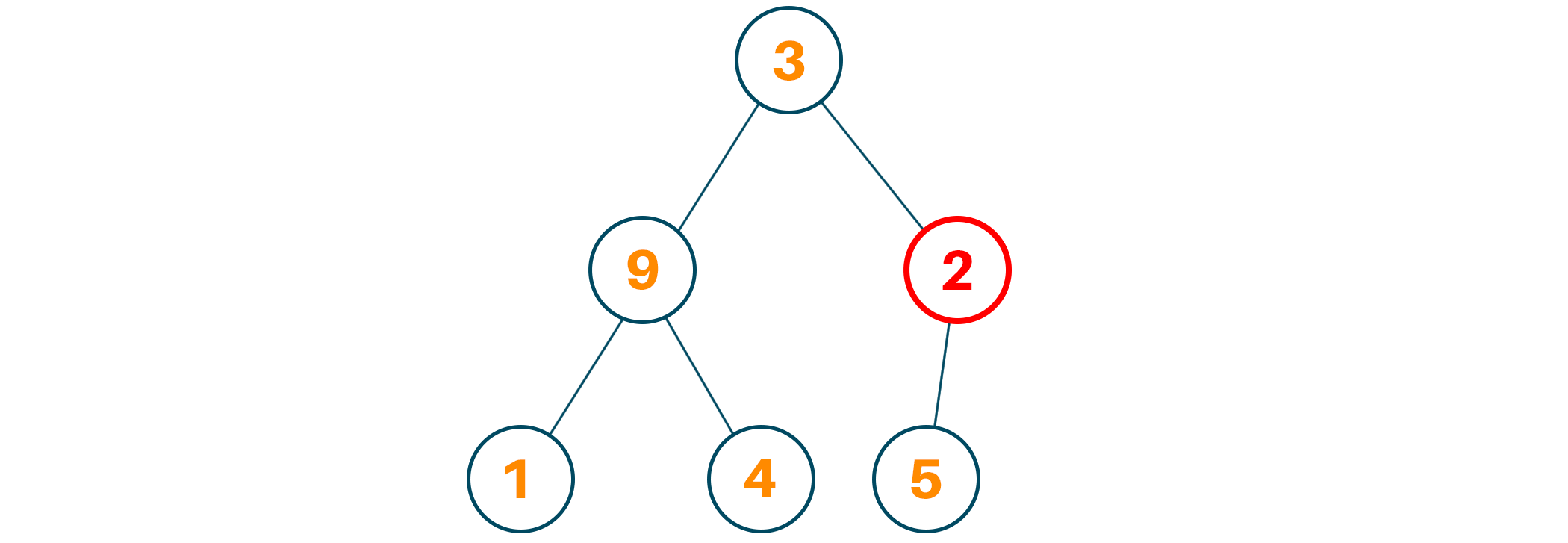
Now we will set the current element “k” as “largest” and as we know the index of a left child is given by “2k + 1” and the right child is given by “2k + 2”.

Therefore, if the left child is larger than the current element i.e. kth index we will set the “largest” with the left child’s index and if the right child is larger than the current element i.e., kth index then we will set the “largest” with right child’s index.

Lastly, we will swap the “largest” element with the current element(kth element).

We’ll repeat the above steps 3-6 until the tree is heaped.

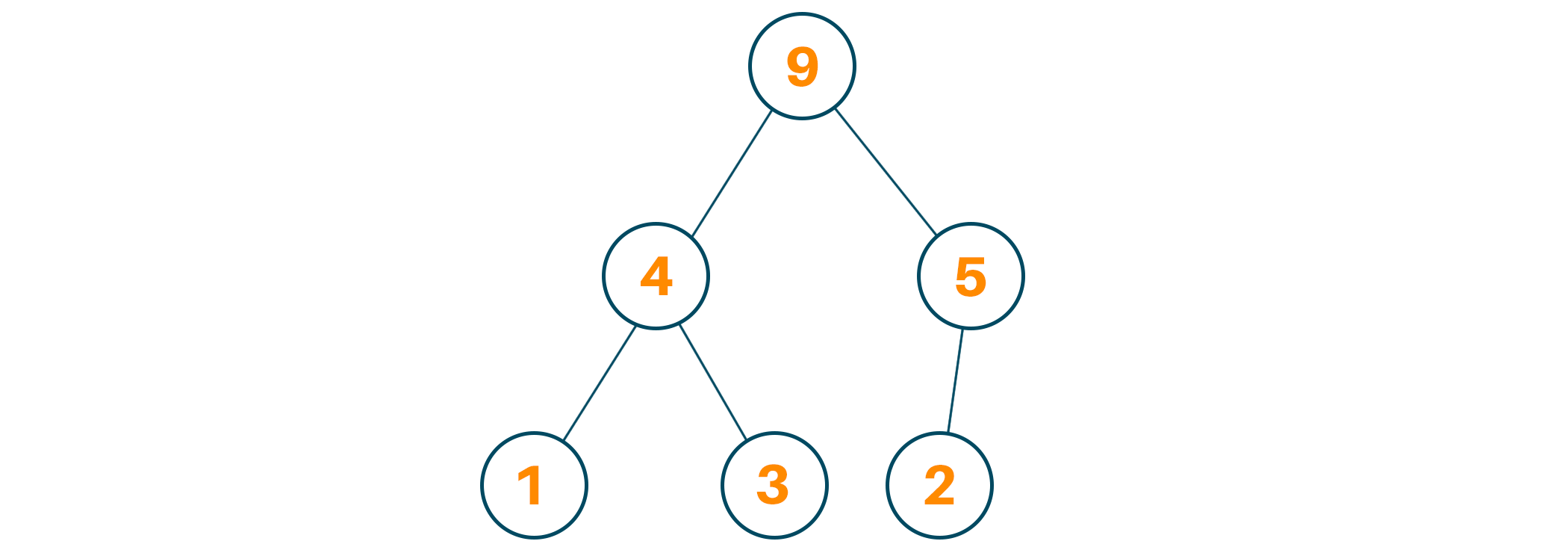
Algorithm for Max-Heapify

maxHeapify(array, size, k)
  set k as largest
  leftChild = 2k + 1
  rightChild = 2k + 2
  
  if leftChild > array[largest]
    set leftChildIndex as largest
  if rightChild > array[largest]
    set rightChildIndex as largest

  swap array[k] and array[largest]

Algorithm for Min-Heapify

minHeapify(array, size, k)
  set k as smallest
  leftChild = 2k + 1
  rightChild = 2k + 2
  
  if leftChild < array[smallest]
    set leftChildIndex as smallest
  if rightChild < array[smallest]
    set rightChildIndex as smallest

  swap array[k] and array[smallest]

What is Max Heap?

When the value of each internal node is larger than or equal to the value of its children node then it is called the Max-Heap Property. Also, in a max-heap, the value of the root node is largest among all the other nodes of the tree. Therefore, if “a” has a child node “b” then

Key(a) >= key(b)

represents the Max-Heap Property. Let us display the max-heap using an array. Therefore, the root node will be arr[0]. So, for kth node i.e., arr[k]:

arr[(k - 1)/2] will return the parent node

arr[(2*k) + 1] will return left child

arr[(2*k) + 2] will return right child

Algorithm for Max Heap

MaxHeap(array, size)
  loop from the first index down to zero
    call maxHeapify

Algorithm for Insertion in Max Heap

If there is no node, 
  create a new Node.
else (a node is already present)
  insert the new Node at the end 
  
maxHeapify the array

Algorithm for Deletion in Max Heap

If nodeDeleted is the leaf Node
  remove the node
Else swap nodeDeleted with the lastNode
  remove nodeDeleted
   
maxHeapify the array

Python Code for Max Heap Data Structure

def max_heapify(A,k):
    l = left(k)
    r = right(k)
    if l < len(A) and A[l] > A[k]:
        largest = l
    else:
        largest = k
    if r < len(A) and A[r] > A[largest]:
        largest = r
    if largest != k:
        A[k], A[largest] = A[largest], A[k]
        max_heapify(A, largest)

def left(k):
    return 2 * k + 1

def right(i):
    return 2 * k + 2

def build_max_heap(A):
    n = int((len(A)//2)-1)
    for k in range(n, -1, -1):
        max_heapify(A,k)

A = [3,9,2,1,4,5]
build_max_heap(A)
print(A)

Output

[9, 4, 5, 1, 3, 2]

What is Min Heap?

When the value of each internal node is smaller than the value of its children node then it is called the Min-Heap Property. Also, in the min-heap, the value of the root node is the smallest among all the other nodes of the tree. Therefore, if “a” has a child node “b” then

Key(a) < key(b)

represents the Min Heap Property. Let us display the max heap using an array. Therefore, the root node will be arr[0]. So, for kth node i.e., arr[k]:

arr[(k - 1)/2] will return the parent node

arr[(2*k) + 1] will return left child

arr[(2*k) + 2] will return right child

Algorithm for Min Heap

MinHeap(array, size)
  loop from the first index down to zero
    call minHeapify 

Algorithm for Insertion in Min Heap

If there is no node, 
  create a new Node.
else (a node is already present)
  insert the new Node at the end 
  
minHeapify the array

Algorithm for Deletion in Min Heap

If nodeDeleted is the leaf Node
  remove the node
Else swap nodeDeleted with the lastNode
  remove nodeDeleted
   
minHeapify the array

Python Code for Min Heap Data Structure

def min_heapify(A,k):
    l = left(k)
    r = right(k)
    if l < len(A) and A[l] < A[k]:
        smallest = l
    else:
        smallest = k
    if r < len(A) and A[r] < A[smallest]:
        smallest = r
    if smallest != k:
        A[k], A[smallest] = A[smallest], A[k]
        min_heapify(A, smallest)

def left(k):
    return 2 * k + 1

def right(k):
    return 2 * k + 2

def build_min_heap(A):
    n = int((len(A)//2)-1)
    for k in range(n, -1, -1):
        min_heapify(A,k)

A = [3,9,2,1,4,5]
build_min_heap(A)
print(A)

Output 

[1, 3, 2, 9, 4, 5]

Min Heap vs Max Heap 

Time complexity

The running time complexity of the building heap is O(n log(n)) where each call for heapify costs O(log(n)) and the cost of building heap is O(n). Therefore, the overall time complexity will be O(n log(n)).

Applications of Heap

• Heap is used while implementing priority queue
• Heap is used in Heap sort
• Heap data structure is used while working with Dijkstra's algorithm
• We can use max-heap and min-heap in the operating system for the job scheduling algorithm
• It is used in the selection algorithm
• Heap data structure is used in graph algorithms like prim’s algorithm
• It is used in order statistics
• Heap data structure is used in k-way merge

Conclusion

Heap data structure is a very useful data structure when it comes to working with graphs or trees. Heap data structure helps us improve the efficiency of various programs and problem statements. We can use min-heap and max-heap as they are efficient when processing data sets. As you get a good command of heap data structure, you are great to work with graphs and trees at the advanced level.