When you are working on a large amount of data, every data element is attached to other data elements. That’s where the non-sequential data structure such as trees, graphs, files, etc comes into the picture. Today, we will discuss one such aspect of Binary Trees and learn how to find the Diameter of a Binary Tree using two different approaches.
What is a Binary Tree?
Before moving forward, we must revise what are Trees and what makes them Binary. As we know, trees are widely used as an abstract data structure that simulates the hierarchical structure to store data. The tree consists of nodes to represent the data as shown in the below image. The topmost node is known as the root node.
A general tree data structure has no limitation for the number of child nodes and leaf nodes. But when it comes to a binary tree, the given condition changes.
A binary tree is a type of tree data structure that possesses a maximum of two children nodes for each parent node. Each of these children's nodes is generally referred to as the left child and right child respectively. The below image represents the binary tree data structure.
As the binary tree is a widely used data structure, you are most likely to face competitive questions related to it while cracking the interview of your dream company. One such question is calculating the diameter of this type of tree.
What is the Diameter of a Binary Tree?
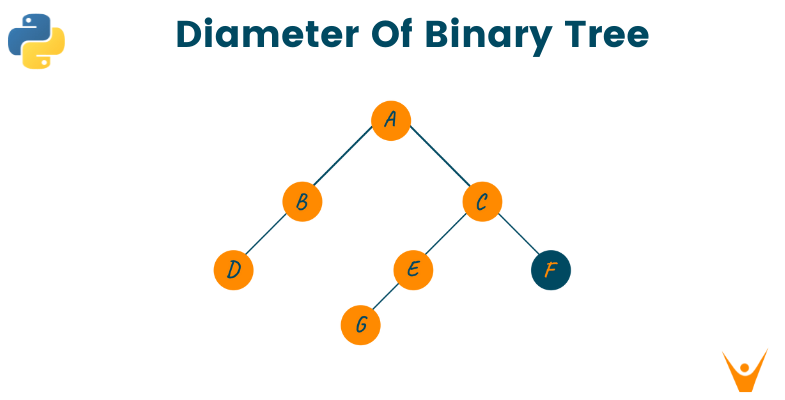
The diameter of the binary tree is defined as the total number of nodes on the longest path between two end nodes. Note that this path does not have to pass through the root node.
For example, the below image shows the diameter of the tree from the left side to the right side passing through the root node.
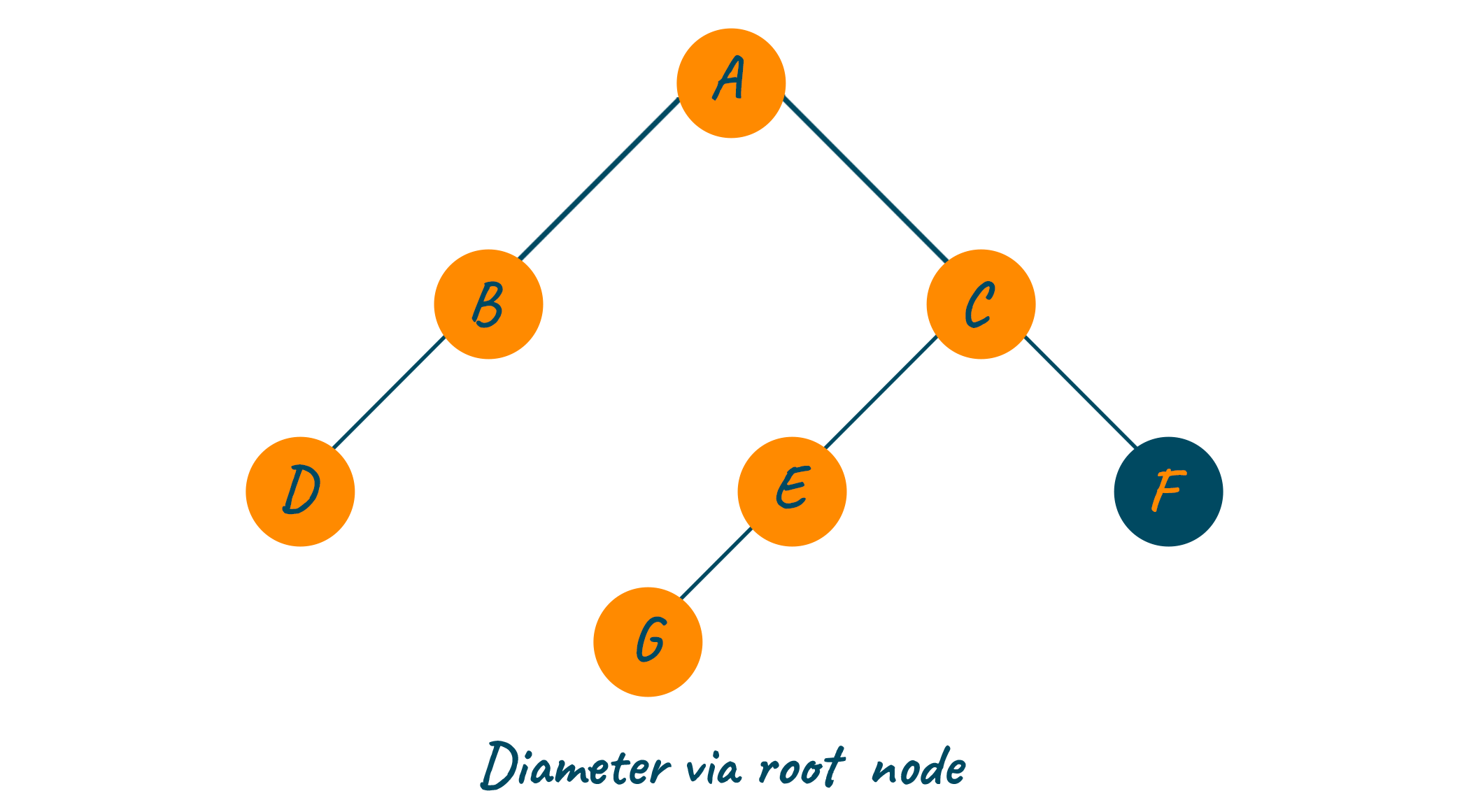
In the above image, the diameter of the binary tree is calculated via the root node i.e., D-B-A-C-E-G. Whereas the below image shows the diameter of the binary tree from the left side to the right side without passing through the root node i.e., G-E-C-F.
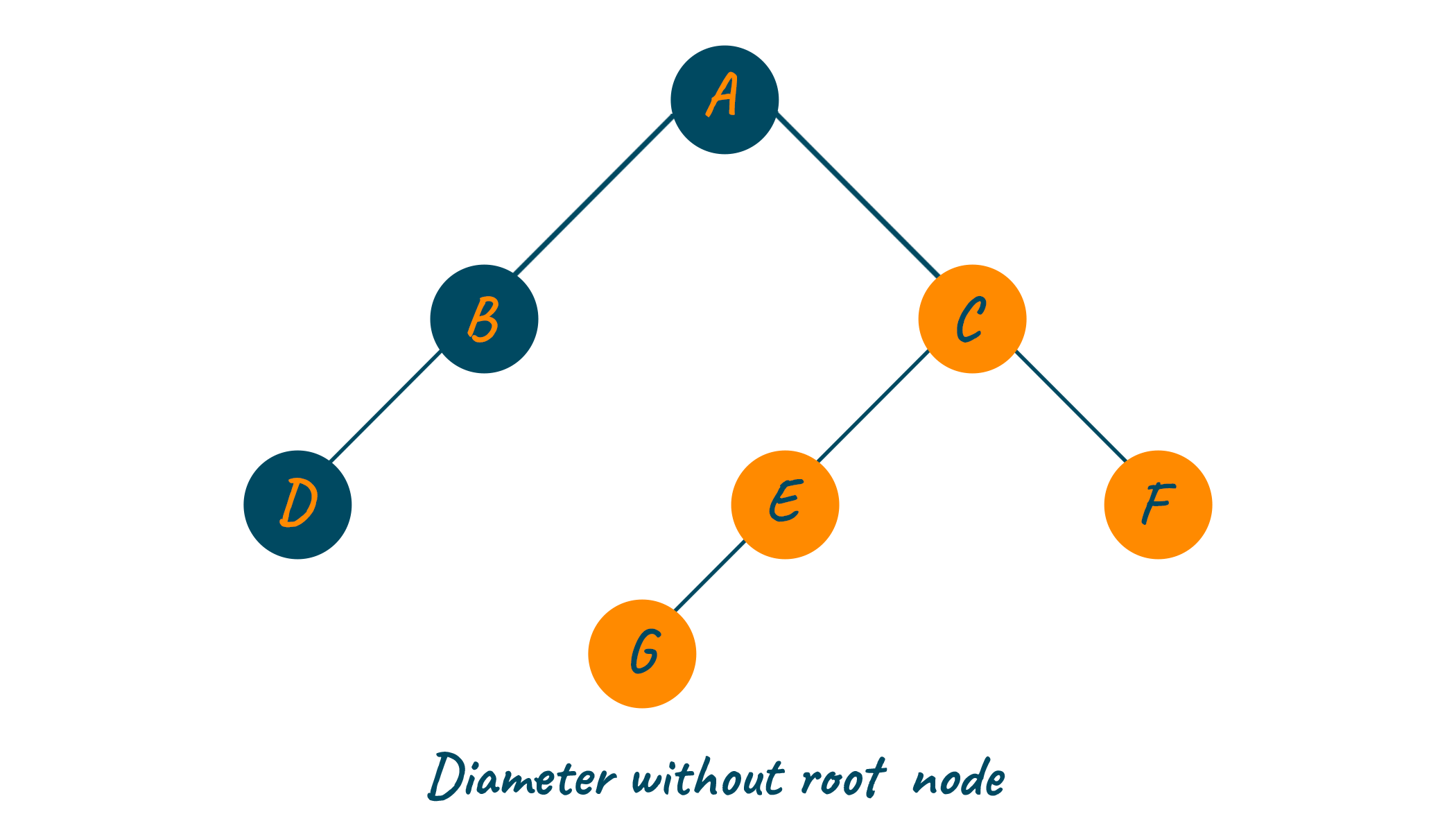
Find the Diameter of a Binary Tree
We have two approaches by which we can calculate the diameter of the binary tree. There is a Recursive approach and there is an Iterative approach. Let's learn about both of them one-by-one:
Diameter of the Binary Tree Using a Recursive Approach
If you observe the above images, the diameter of the binary tree is the maximum sum of the heights of the left subtree and right subtree. Also, the diameter of every subtree may or may not include the sub-root in the calculation. If it does, then the final equation for the diameter of the binary tree will be:
Diameter = Left subtree height + Right subtree height + 1
Using the recursive approach, you can calculate the height of the left subtree and right subtree recursively from the left node. Later, calculate the diameter of the left-subtree and right-subtree as shown in the below visual. The maximum of both will be your final output.
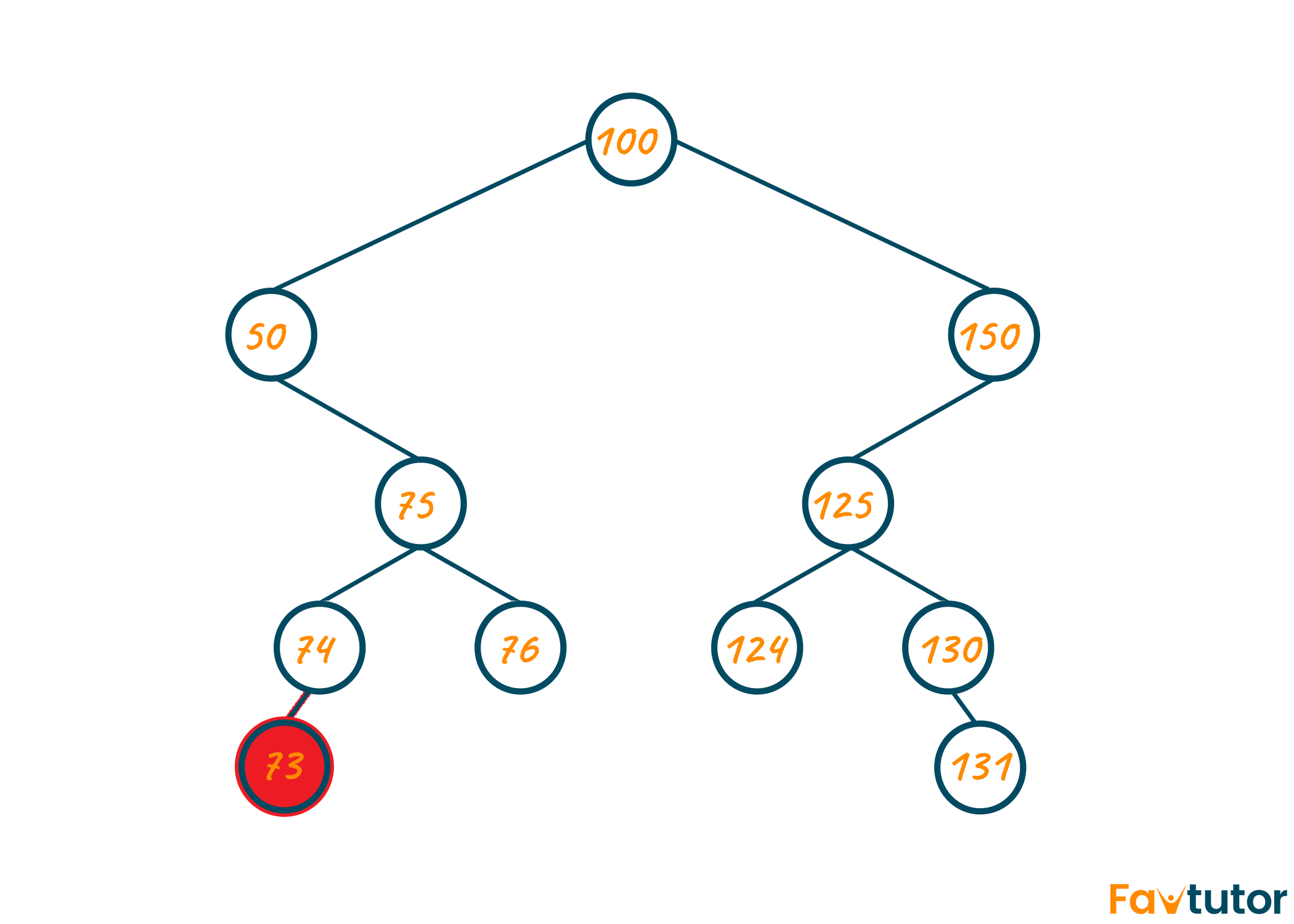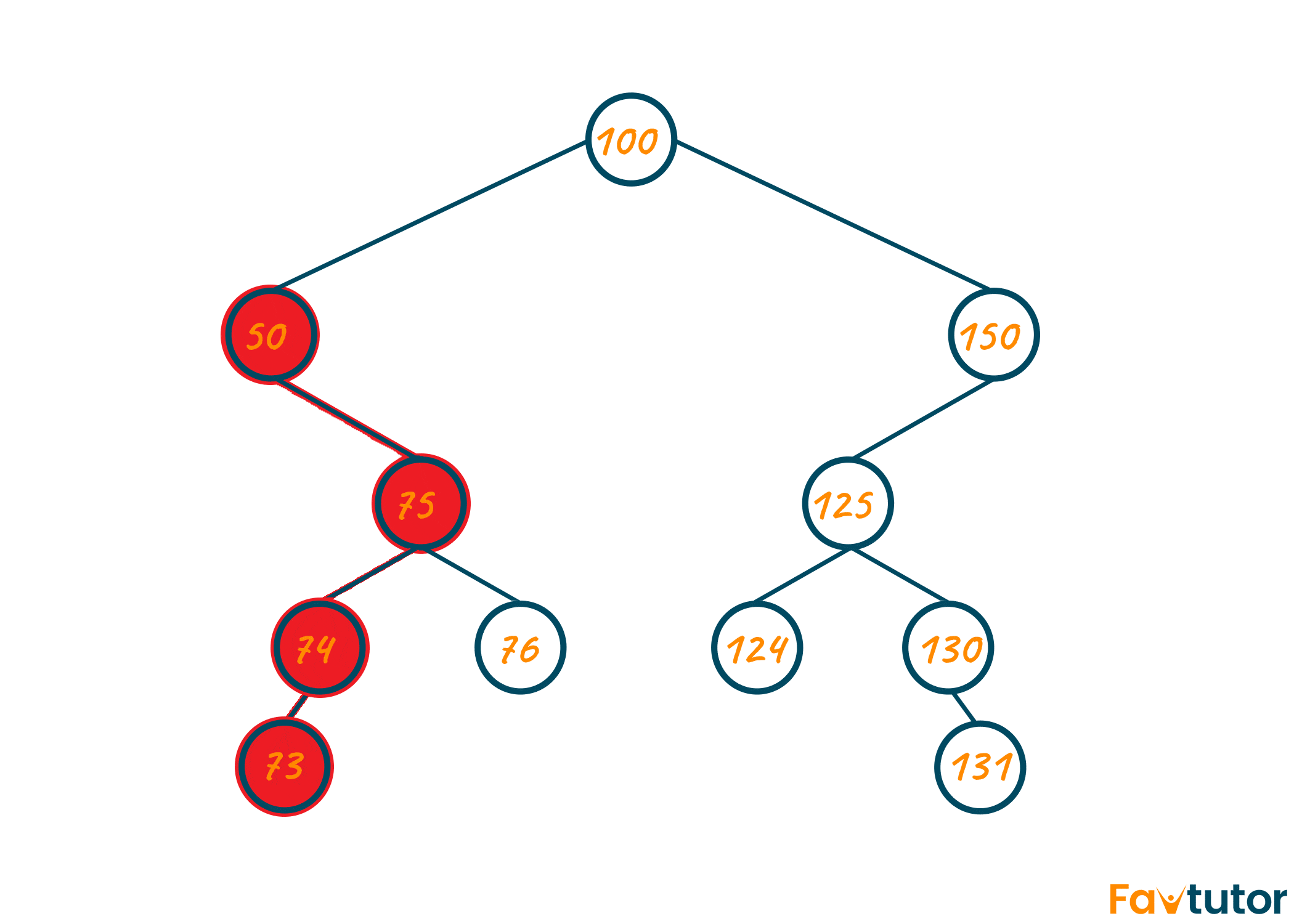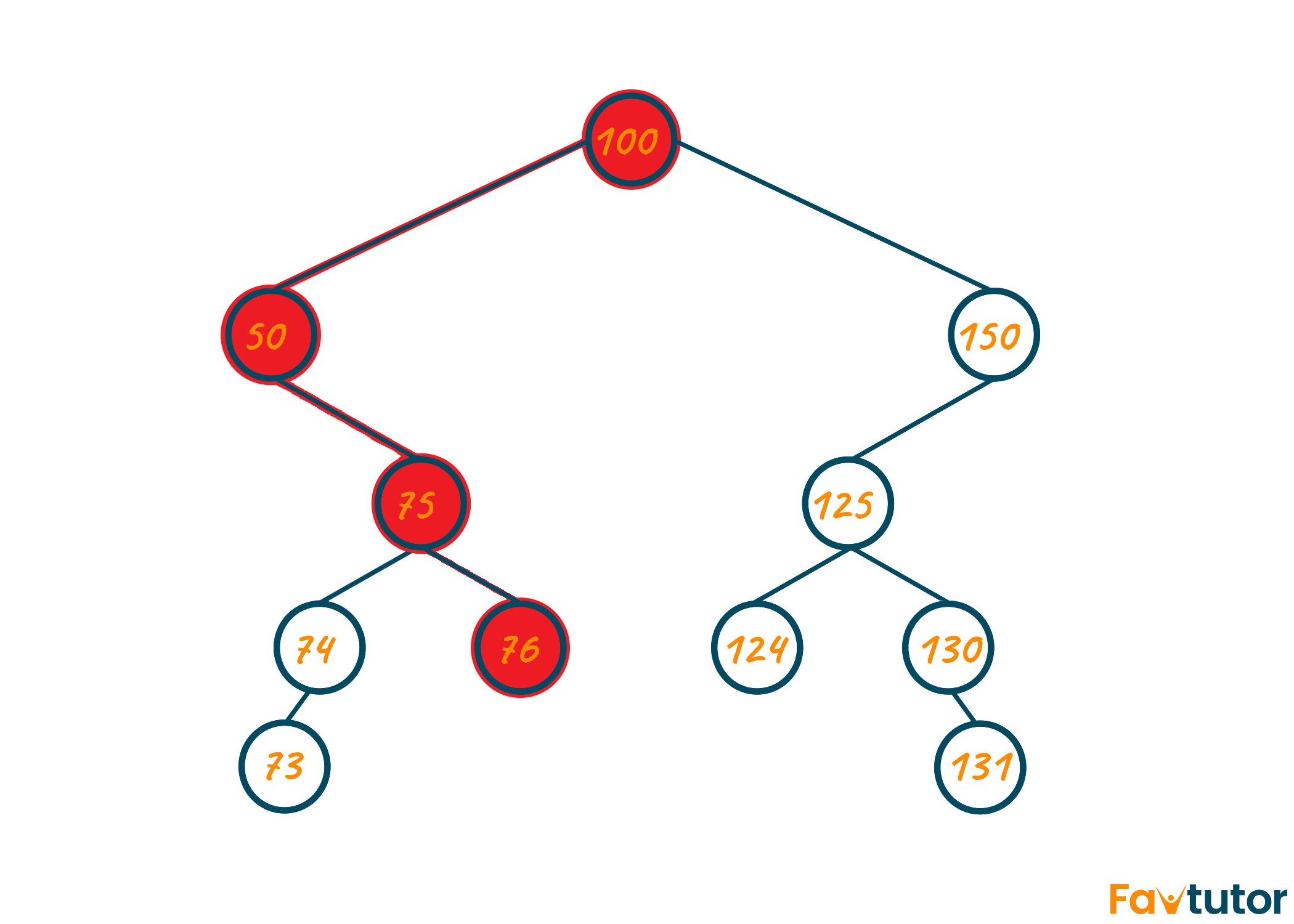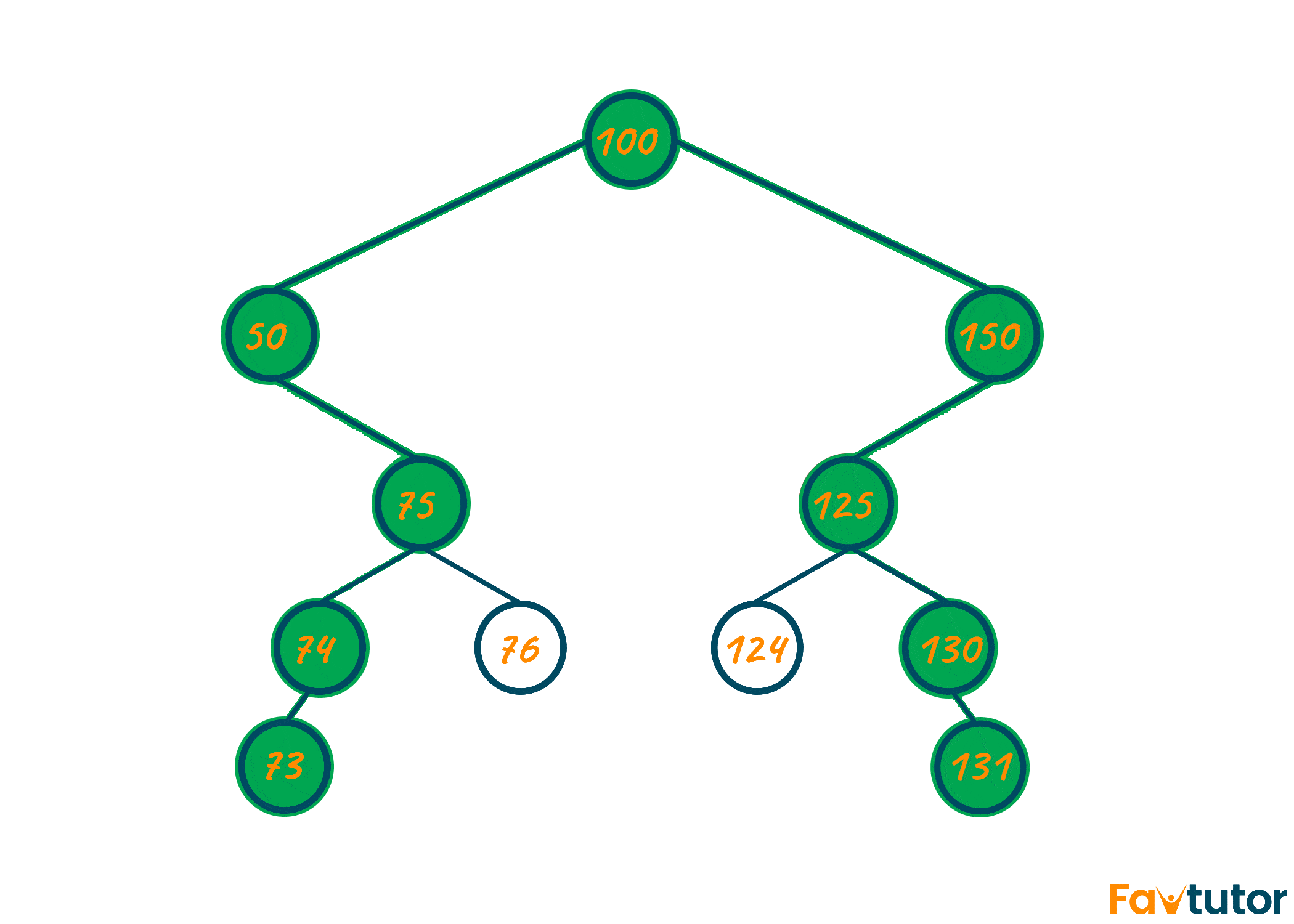
As seen in the above illustration, there are multiple options for the diameter of a binary tree. However, at last, we should choose the option displaying the longest diameter of the binary tree shown in the green color which is 73-74-75-50-100-150-125-130-131.
Below is the algorithm for the recursive approach:
1) Node passed in recursive function is null then return zero 2) Find the height of the left subtree 3) Find the height of the right subtree 4) Using recursive call, calculate the diameter of left-subtree until node becomes NULL 5) Using recursive call, calculate the diameter of right-subtree until node becomes NULL 6) If the root node is included then, Diameter = left-subtree + right-subtree + 1 7) If the root node is not included then, Diameter = max(diameter of left-subtree, diameter of right subtree) 8) The final output will return the max of step 6 and step 7
Repeat the above process recursively until NULL nodes are encountered.
Now that we know the algorithm, we can easily write a program. Below we have given the Python implementation to find the diameter of a tree using recursion:
class TreeNode: ''' Tree Node ''' def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def __init__(self): self.max = 0 def Diameter(self, root: TreeNode) -> int: if root is None: return 0 def traverse(root): if root is None: return 0 left = traverse(root.left) right = traverse(root.right) if left + right > self.max: self.max = left+right return max(left, right) + 1 traverse(root) return self.max if __name__ == '__main__': root = TreeNode(10) root.left = TreeNode(11) root.left.left = TreeNode(2) root.left.right = TreeNode(31) root.right = TreeNode(12) print(Solution().Diameter(root))
Output:
3
The time complexity of the above approach is O(n^2) where n is the number of nodes in the tree. It is because, the function recursively calls itself, and hence, every node is visited at least twice while calculating the diameter. However, the space complexity of the recursive approach is O(n) because of recursion.
Diameter of the Binary Tree Using an Iterative Approach
You can also find the diameter of the binary tree using the iterative approach of the Depth First Search algorithm.
As the diameter is always defined as the path between two leaf nodes of a binary tree, if you find the farthest node from the leaf node, you can easily calculate the diameter of the tree. This method is also called the Iterative method and provides me with the optimized solution for calculating the diameter of a binary tree.
Below is the algorithm for the iterative approach:
1) Starting from the root node, find the farthest node in the binary tree using the DFS algorithm 2) Consider this farthest node as the initial node of the diameter of the binary tree 3) Again, using the DFS algorithm, calculate the farthest node from the initial node found in step 2. 4) Newly found farthest node will be the end node of the diameter of binary tree
Below we have given the Python implementation to find the diameter of a tree using the iterative approach:
from collections import deque class TreeNode: ''' Tree Node ''' def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right class Solution: def Diameter(self , root: TreeNode ): ''' Function to find depth of the Binary Tree :param root: Root Node :return: Depth of the tree ''' stack = deque ( [ root ] ) depth = {None : 0} ans = 0 while stack : node = stack.pop () if not node : continue LDepth = depth.get ( node.left , None ) RDepth = depth.get ( node.right , None ) if LDepth== None or RDepth == None : stack.append ( node ) stack.append ( node.left ) stack.append ( node.right ) continue depth [ node ] = max ( LDepth, RDepth ) + 1 ans = max ( LDepth+ RDepth , ans ) return ans if __name__ == '__main__': root = TreeNode(10) root.left = TreeNode(11) root.left.left = TreeNode(2) root.left.right = TreeNode(31) root.right = TreeNode(12) print(f'Diameter is : {Solution().Diameter(root)}')
Output:
Diameter is : 3
The time complexity using this approach is O(n) and therefore, it is considered to be an optimized solution for calculating the diameter of a binary tree. It is because using the iterative approach, we only visit the nodes of the tree once. At the same time, the space complexity of this approach is also O(n) where n is the number of nodes present in the tree.
Find the Diameter of a Rooted Binary Tree
A binary tree can be of two types. First is the Rooted Binary Tree which consists of the root nodes and every node has a maximum of two children nodes. The second is Fully Binary Tree consists of the root node and every other node in the tree has either 0 or 2 children exactly.
In Rooted Binary Tree, its diameter is the longest path between any two nodes in the tree. In other terms, the diameter of a binary tree is the number of edges that can exist between any two leaf nodes in the tree.
To calculate the diameter of a binary tree, first compute the heights of all subtrees rooted at each node, and then compute the highest diameter seen so far. Below is the Python code to calculate the diameter of a rooted binary tree:
class Node: def __init__(self, data): self.left = None self.right = None self.data = data def height(node): if node is None: return 0 else: left_height = height(node.left) right_height = height(node.right) return max(left_height, right_height) + 1 def diameter(node): if node is None: return 0 # Get the heights of the left and right subtrees left_height = height(node.left) right_height = height(node.right) # Get the diameter of the left and right subtrees left_diameter = diameter(node.left) right_diameter = diameter(node.right) # Return the maximum of the following: # 1) Diameter of the left subtree # 2) Diameter of the right subtree # 3) Length of the path passing through the root return max(left_height + right_height, max(left_diameter, right_diameter)) # Sample Usage # Create a sample binary tree # 1 # / \ # 2 3 # / \ # 4 5 root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)
Output:
Diameter of the binary tree is 3
Conclusion
Finding the diameter of a binary tree is one of the fundamental problems and now you know how to calculate it using Python. In the real world, it is used to calculate the route during inter-processor communication within the network of any structure. If you got some questions about it in your homework, we have premium Data Structure Assignment Help to assist you online.