Depth First Search in Python (with Code) | DFS Algorithm

Traversal means that visiting all the nodes of a graph which can be done through Depth-first search or Breadth-first search in python. Depth-first traversal or Depth-first Search is an algorithm to look at all the vertices of a graph or tree data structure. Here we will study what depth-first search in python is, understand how it works with its bfs algorithm, implementation with python code, and the corresponding output to it. 

What is Depth First Search?

What do we do once have to solve a maze? We tend to take a route, keep going until we discover a dead end. When touching the dead end, we again come back and keep coming back till we see a path we didn't attempt before. Take that new route. Once more keep going until we discover a dead end. Take a come back again… This is exactly how Depth-First Search works.

The Depth-First Search is a recursive algorithm that uses the concept of backtracking. It involves thorough searches of all the nodes by going ahead if potential, else by backtracking. Here, the word backtrack means once you are moving forward and there are not any more nodes along the present path, you progress backward on an equivalent path to seek out nodes to traverse. All the nodes are progressing to be visited on the current path until all the unvisited nodes are traversed after which subsequent paths are going to be selected.

DFS Algorithm

Before learning the python code for Depth-First and its output, let us go through the algorithm it follows for the same. The recursive method of the Depth-First Search algorithm is implemented using stack. A standard Depth-First Search implementation puts every vertex of the graph into one in all 2 categories: 1) Visited 2) Not Visited. The only purpose of this algorithm is to visit all the vertex of the graph avoiding cycles.

The DSF algorithm follows as:

1. We will start by putting any one of the graph's vertex on top of the stack.
2. After that take the top item of the stack and add it to the visited list of the vertex.
3. Next, create a list of that adjacent node of the vertex. Add the ones which aren't in the visited list of vertexes to the top of the stack.
4. Lastly, keep repeating steps 2 and 3 until the stack is empty.

DFS pseudocode

The pseudocode for Depth-First Search in python goes as below: In the init() function, notice that we run the DFS function on every node because many times, a graph may contain two different disconnected part and therefore to make sure that we have visited every vertex, we can also run the DFS algorithm at every node.

DFS(G, u)

    u.visited = true

    for each v ∈ G.Adj[u]

        if v.visited == false

            DFS(G,v)   

init() {

    For each u ∈ G

        u.visited = false

     For each u ∈ G

       DFS(G, u)

}

DFS Implementation in Python (Source Code)

Now, knowing the algorithm to apply the Depth-First Search implementation in python, we will see how the source code of the program works.

Consider the following graph which is implemented in the code below:

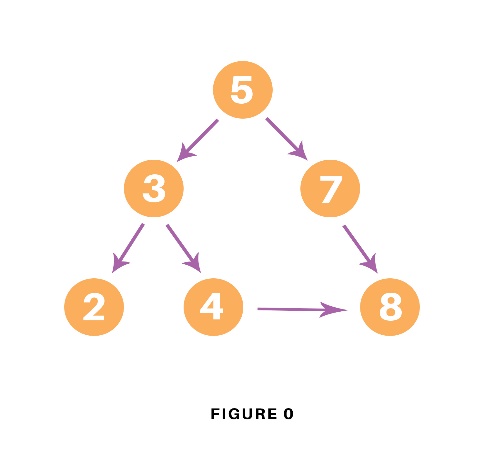
# Using a Python dictionary to act as an adjacency list
graph = {
  '5' : ['3','7'],
  '3' : ['2', '4'],
  '7' : ['8'],
  '2' : [],
  '4' : ['8'],
  '8' : []
}

visited = set() # Set to keep track of visited nodes of graph.

def dfs(visited, graph, node):  #function for dfs 
    if node not in visited:
        print (node)
        visited.add(node)
        for neighbour in graph[node]:
            dfs(visited, graph, neighbour)

# Driver Code
print("Following is the Depth-First Search")
dfs(visited, graph, '5')

In the above code, first, we will create the graph for which we will use the depth-first search. After creation, we will create a set for storing the value of the visited nodes to keep track of the visited nodes of the graph.

After the above process, we will declare a function with the parameters as visited nodes, the graph itself and the node respectively. And inside the function, we will check whether any node of the graph is visited or not using the “if” condition. If not, then we will print the node and add it to the visited set of nodes.

Then we will go to the neighboring node of the graph and again call the DFS function to use the neighbor parameter.

At last, we will run the driver code which prints the final result of DFS by calling the DFS the first time with the starting vertex of the graph.

Output

The output of the above code is as follow:

Following is the Depth-First Search
5 3 2 4 8 7

Example

Let us see how the DFS algorithm works with an example. Here, we will use an undirected graph with 5 vertices.

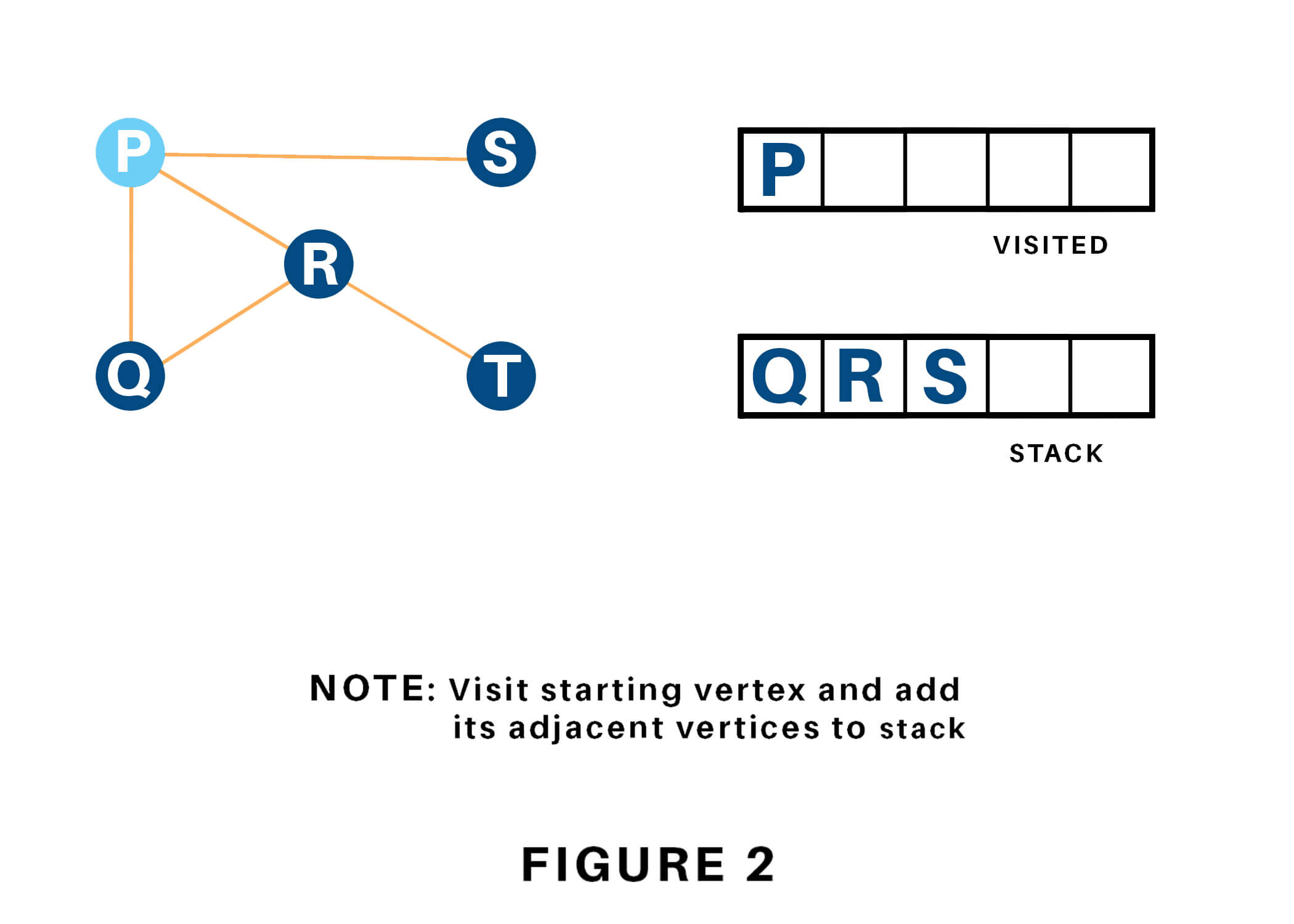
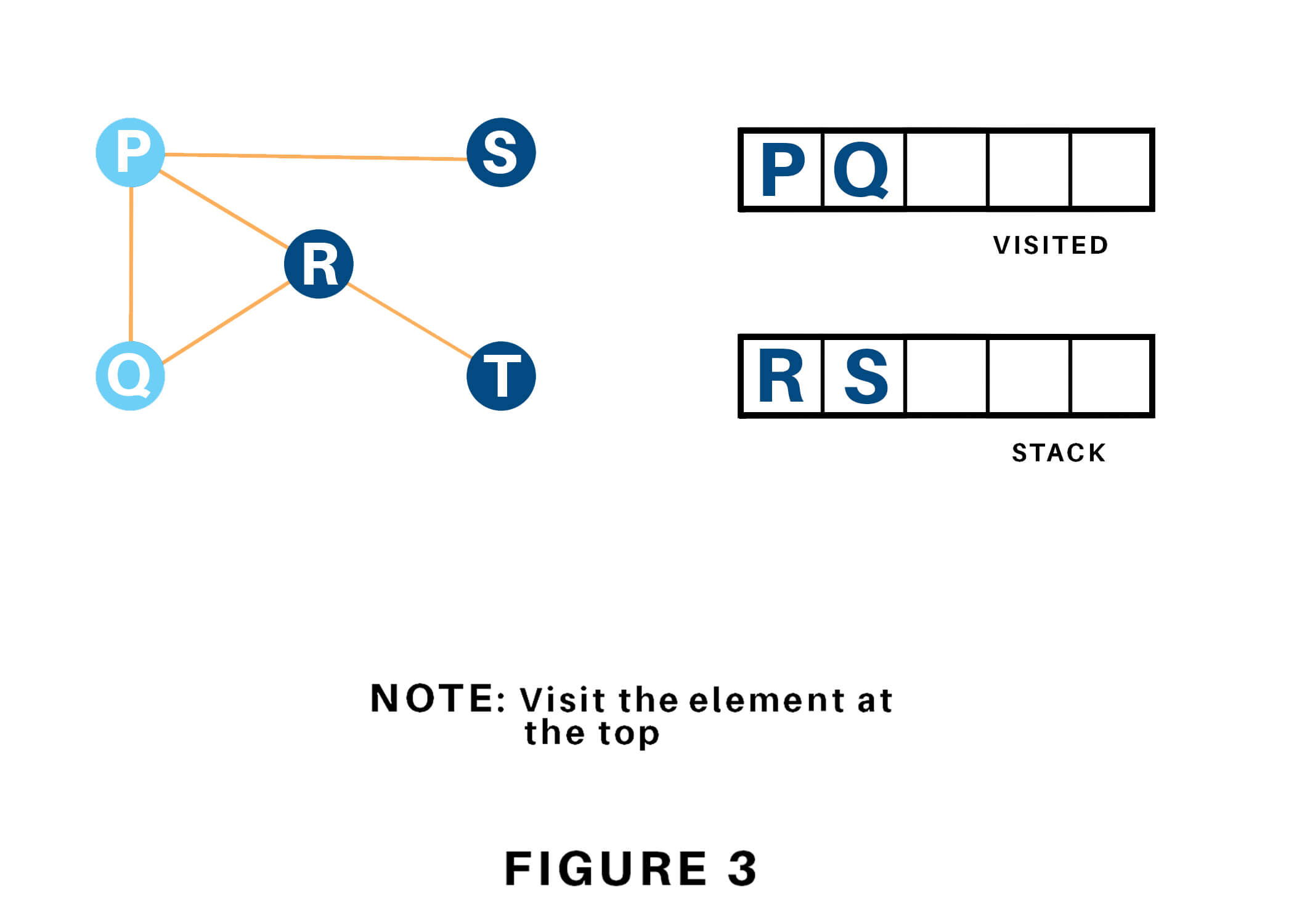
We begin from the vertex P, the DFS rule starts by putting it within the Visited list and putting all its adjacent vertices within the stack.

Next, we tend to visit the part at the highest of the stack i.e. Q, and head to its adjacent nodes. Since P has already been visited, we tend to visit R instead.

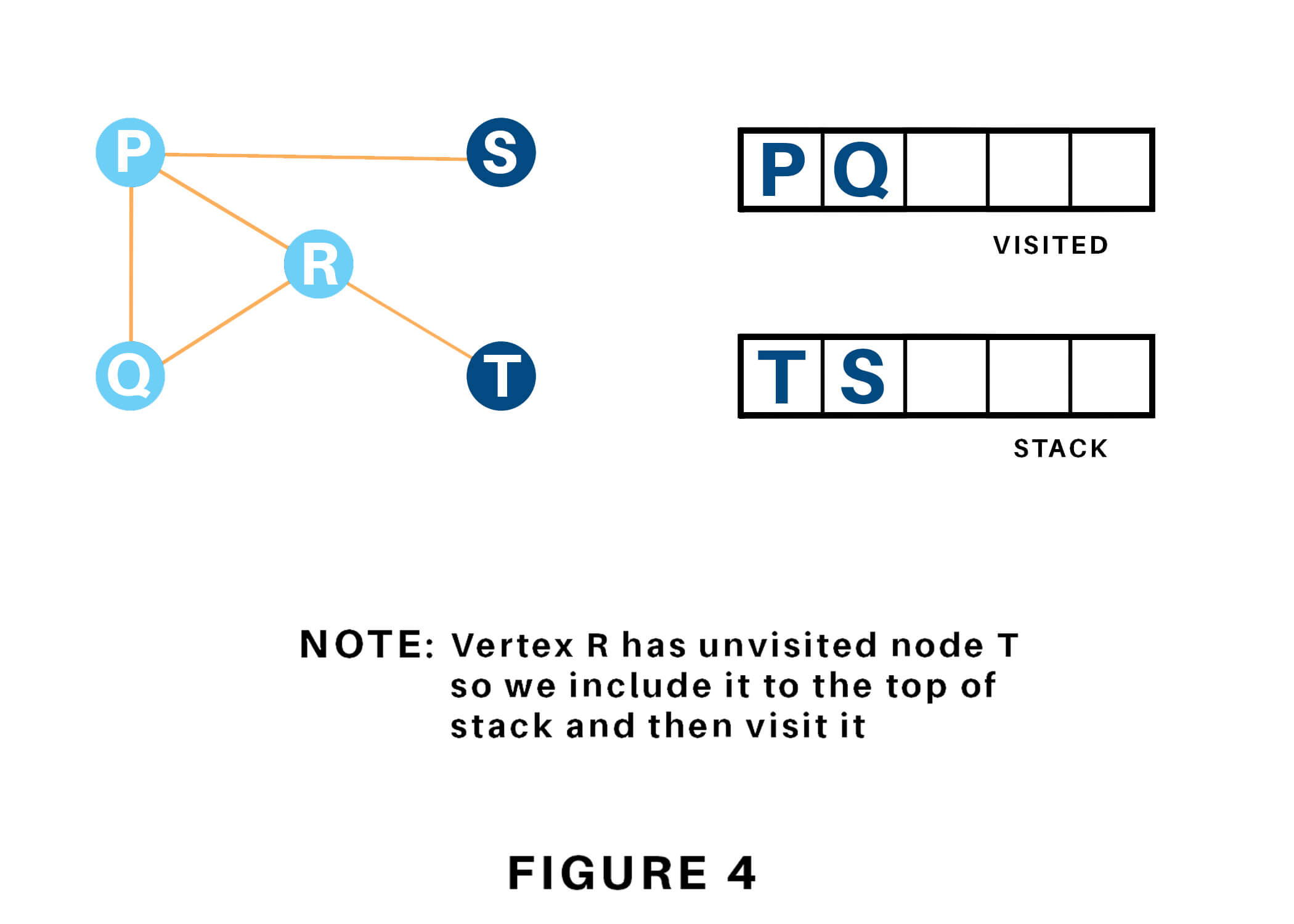
Vertex R has the unvisited adjacent vertex in T, therefore we will be adding that to the highest of the stack and visit it.

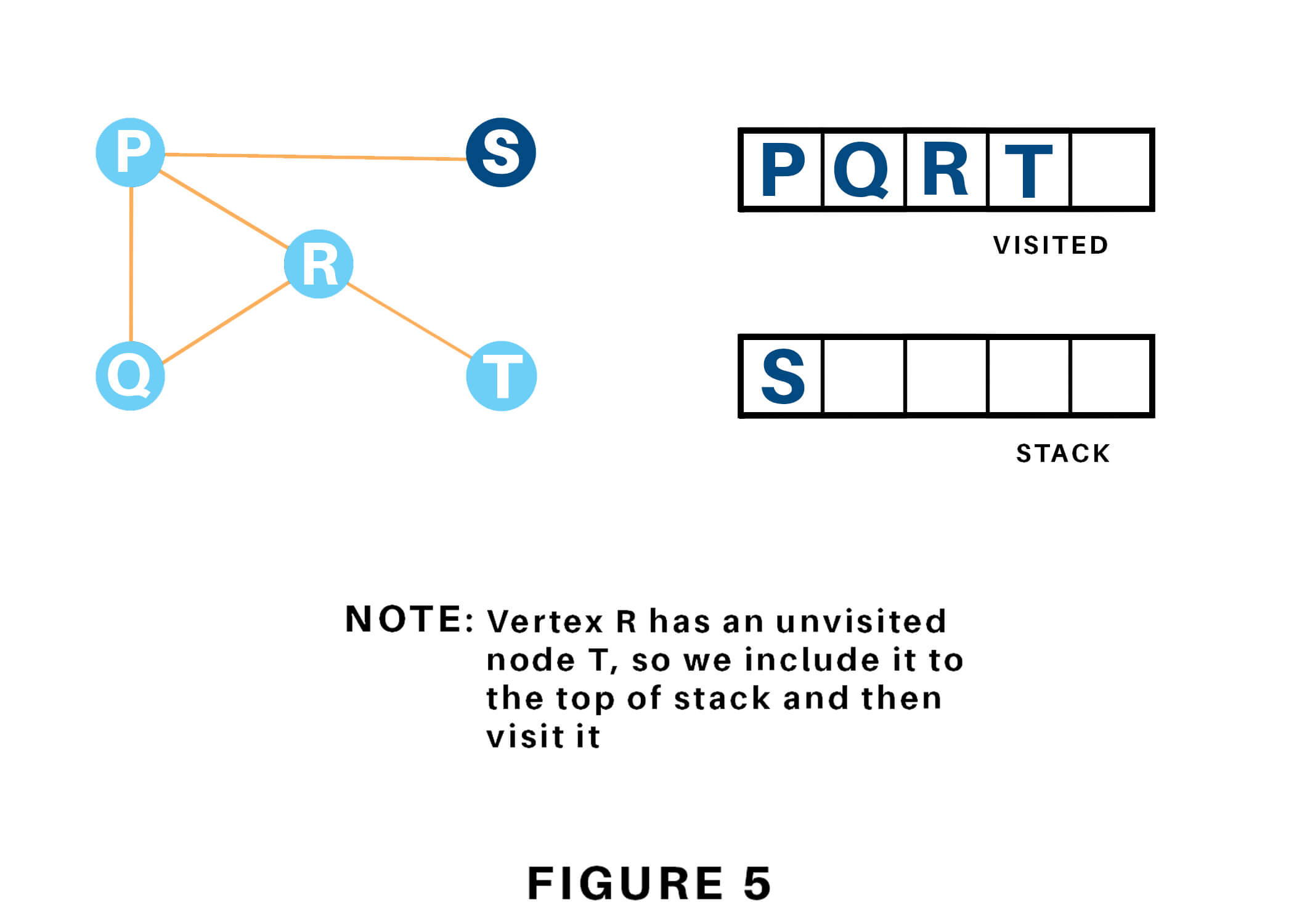
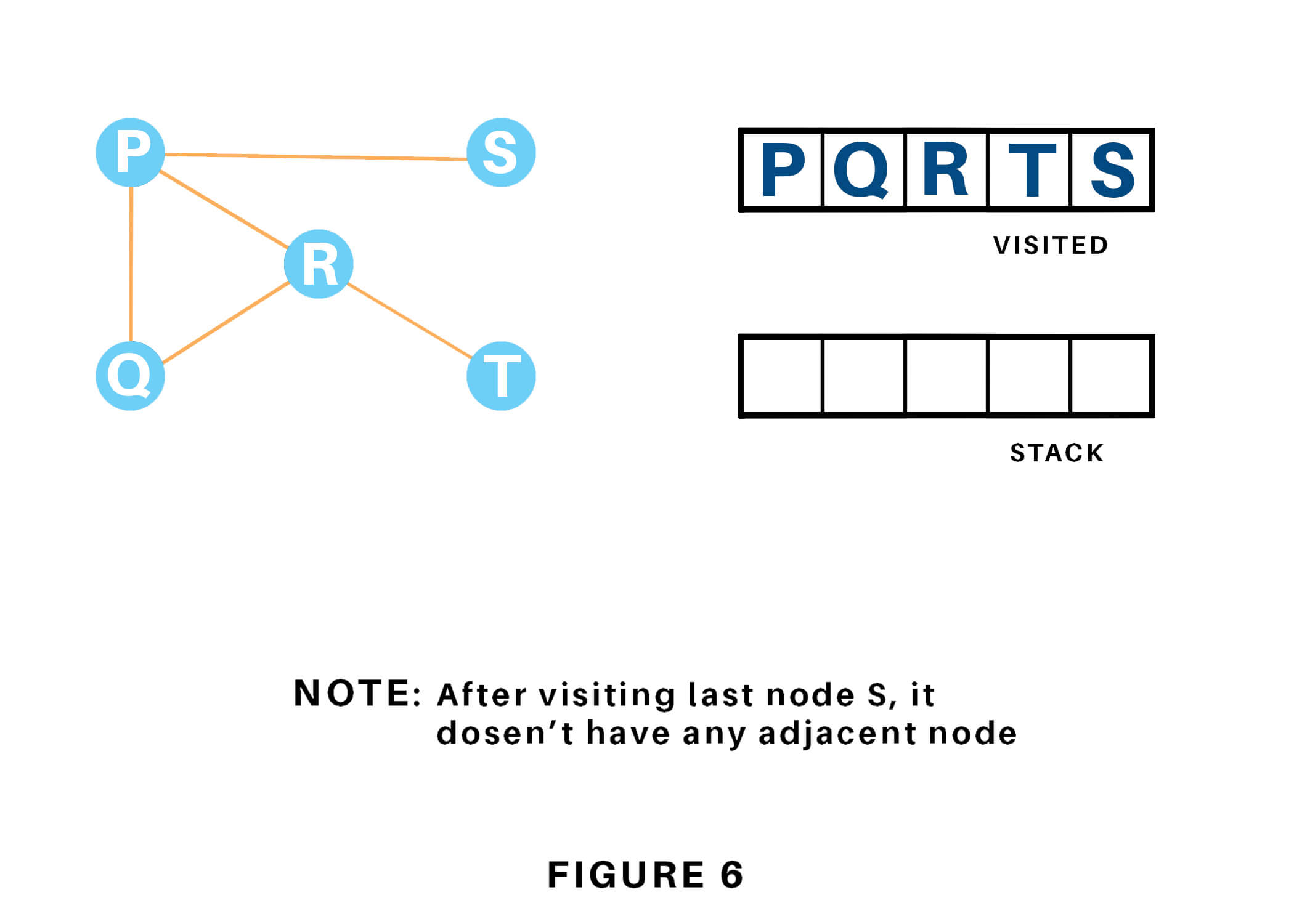
At last, we will visit the last component S, it does not have any unvisited adjacent nodes, thus we've completed the Depth First Traversal of the graph.

Time Complexity

The time complexity of the Depth-First Search algorithm is represented within the sort of O(V + E), where V is that the number of nodes and E is that the number of edges.

The space complexity of the algorithm is O(V).

Applications

Depth-First Search Algorithm has a wide range of applications for practical purposes. Some of them are as discussed below:

1. For finding the strongly connected components of the graph
2. For finding the path
3. To test if the graph is bipartite
4. For detecting cycles in a graph
5. Topological Sorting
6. Solving the puzzle with only one solution.
7. Network Analysis
8. Mapping Routes
9. Scheduling a problem

Conclusion

Hence, Depth-First Search is used to traverse the graph or tree. By understanding this article, you will be able to implement Depth-First Search in python for traversing connected components and find the path.