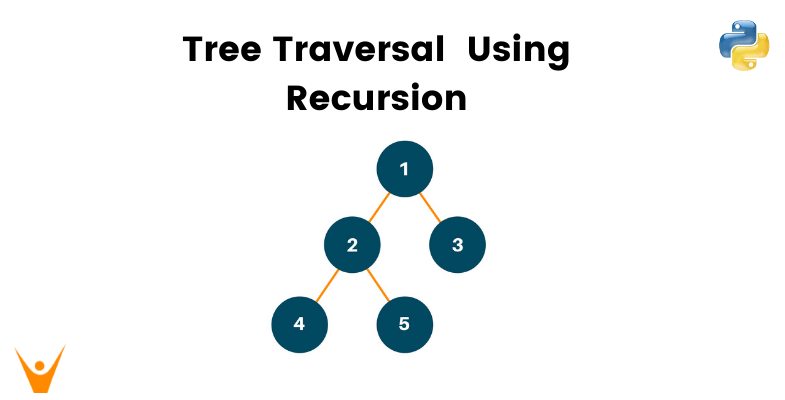
Tree Traversal in Python Using Recursion (With Code)

In this article, we will study what is tree traversal and the implementation of Inorder, Preorder, and Postorder tree traversal in python using recursion. It is the most important topic to learn while learning data structure using python. We will also study the examples and the corresponding outputs for the same. 

What is tree traversal?

Traversal is the process of traversing the node of the data structure. But if we use the data structure like the stack, queue, or linked list then it becomes difficult for traversing the nodes because this data structure is linear, and hence the time complexity of traversal increases. Therefore, we use tree data structures (especially binary trees) when we have to perform the traversal process and find the elements easily. Using tree data structure, it becomes easy to traverse the nodes compared to other data structures because trees store the elements hierarchically, and hence, we can traverse the elements with their priority and path accordingly. Now, there are 3 main methods for tree traversal in python with recursion using DFS which are:

1. Inorder Traversal (left, root, right)
2. Preorder Traversal (root, left, right)
3. Postorder Traversal (left, right, root)

Remember that we will use the recursive function while traversing the tree and call the function again and again until we will traverse all the nodes of the tree.

Apart from this, we can also find the tree traversal without using the recursion method. The only difference between these two methods is that the tree traversal in python without using the recursion process utilizes the stack data structure while tree traversal in python with recursion utilizes array data structure.

Now let us study the above methods of traversing the tree in python with recursion process:

Inorder Tree Traversal

Using the inorder traversal method, we first visit the left subtree of the original tree. Then we will traverse the root node of the tree and lastly the right subtree of the original tree.

Algorithm for Inorder Tree Traversal using Python

1. Calling Inorder (left-subtree)
2. Visit the root node
3. Calling Inorder (right subtree)

For Example:

Let us consider the following binary tree:

Now according to the inorder tree traversal method in python, we first traverse the left subtree of the original tree. Remember, even while traversing the left subtree, we will follow the same process i.e left -> root -> right if the left child node of the original tree has furthermore child nodes. After traversing the left subtree, we will add the result in the array as shown below.

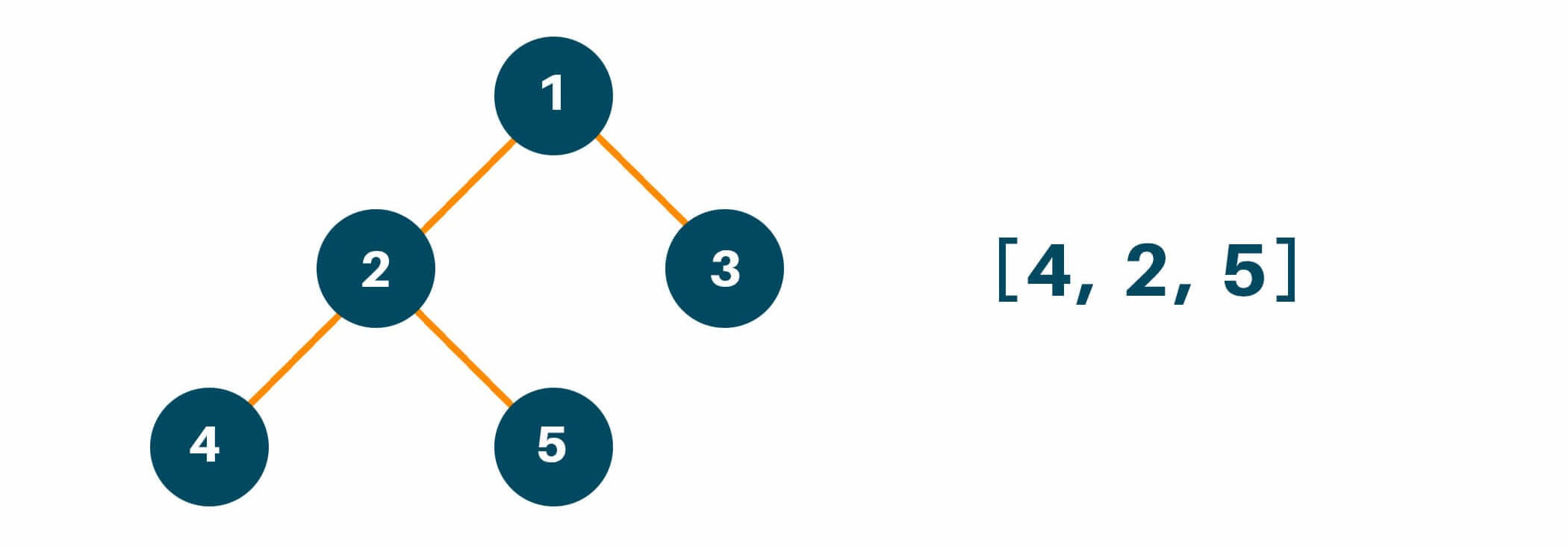
After following the first step, we will traverse the root node of the original tree as shown below.

Lastly, we will traverse the right subtree following the same process i.e left -> root -> right if the right child node of the original tree has more than one child node.

Python code for Inorder Tree Traversal with recursion

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None 

def inorderTraversal(root):
    answer = []

    inorderTraversalUtil(root, answer)
    return answer

def inorderTraversalUtil(root, answer):

    if root is None:
        return

    inorderTraversalUtil(root.left, answer)
    answer.append(root.val)
    inorderTraversalUtil(root.right, answer)
    return

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(inorderTraversal(root))

Output:

[4, 2, 5, 1, 3]

Preorder Tree Traversal

Using the preorder traversal method, we first visit the root of the original tree. Then we will traverse the left subtree of the original tree and lastly the right subtree of the original tree.

Algorithm for Preorder Tree Traversal using Python

1. Visit the root node
2. Calling preorder (left-subtree)
3. Calling preorder (right subtree)

For Example:

Let us consider the following example tree:

According to the preorder traversal method, we will first traverse the root node of the original tree and put it in the result array as shown in the figure below.

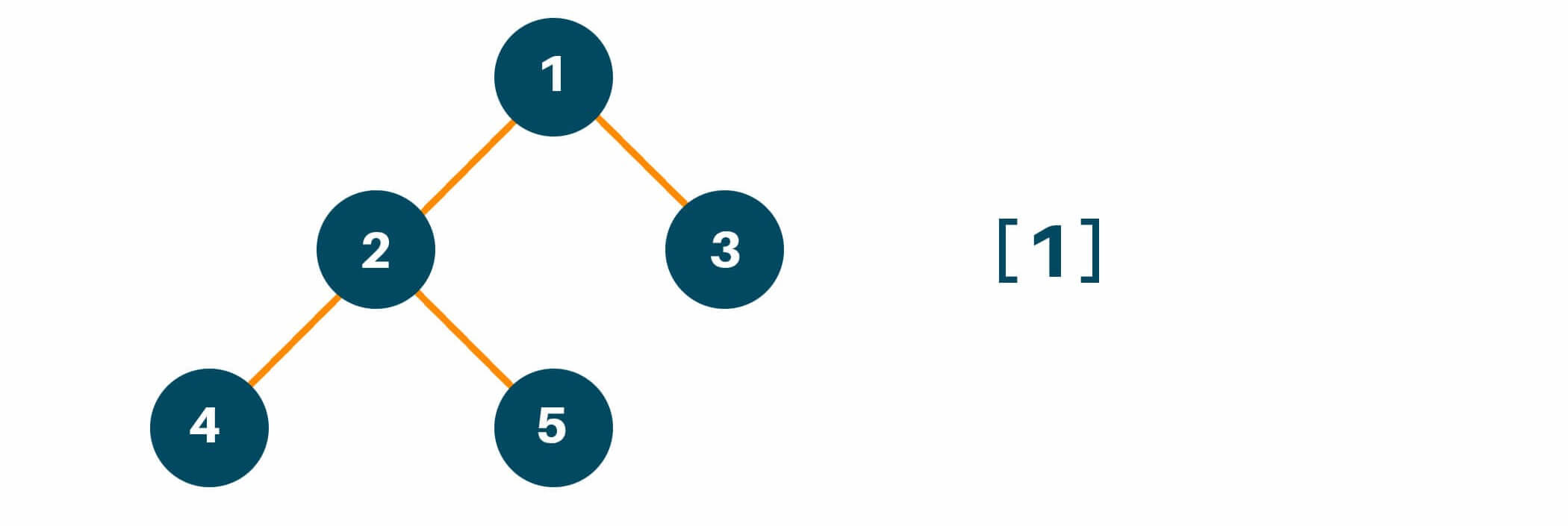
Then, we will traverse the left subtree of the original tree by calling the preorder traversal method. Here we will recursively call the function preorder to maintain the same process of traversal i.e root -> left -> right if the left child of the original tree has more than one child node and add the answer in the array as shown in the figure below.

Lastly, we will traverse the right subtree of the original tree similarly like we did with the left subtree and put the result in the answer array as shown below.

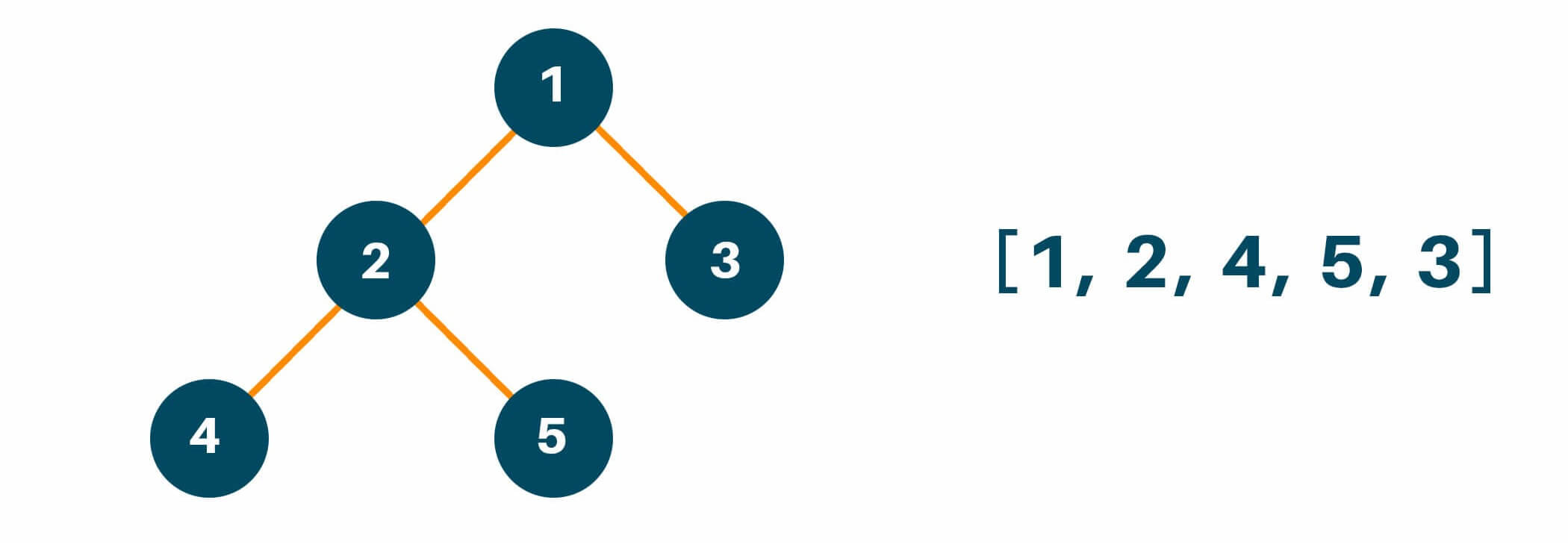
Python code of Preorder Tree Traversal with recursion

class TreeNode:

    def __init__(self,val):
        self.val = val
        self.left = None
        self.right = None

def preorderTraversal(root):
    answer = []

    preorderTraversalUtil(root, answer)
    return answer

def preorderTraversalUtil(root, answer):

    if root is None:
        return 

    answer.append(root.val)

    preorderTraversalUtil(root.left, answer)

    preorderTraversalUtil(root.right, answer)

    return

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(preorderTraversal(root))

Output:

[1, 2, 4, 5, 3]

Postorder Tree Traversal

Using the postorder tree traversal method we first visit the left subtree of the original tree followed by the right subtree and lastly the root node of the original tree.

Algorithm of Postorder Tree Traversal using Python

1. Calling left-subtree
2. Calling right-subtree
3. Visit root node

For Example:

Let us consider the following example tree:

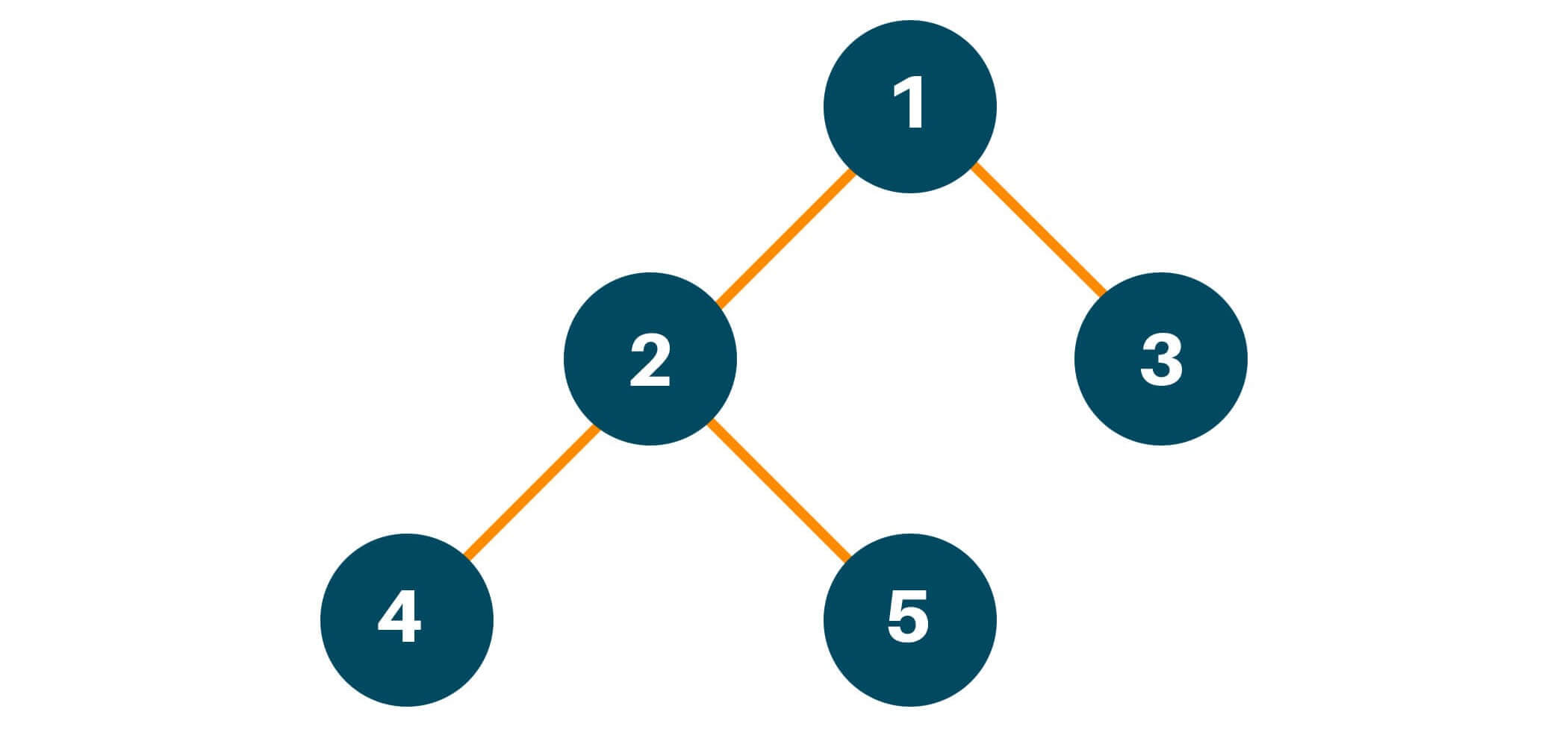
Using the postorder traversal method, we will first traverse the left subtree of the original tree. Remember that we will follow the same process of traversing of left subtree i.e left -> right -> root if the left subtree has more than one child node and then put the result in the answer array as shown in the figure.

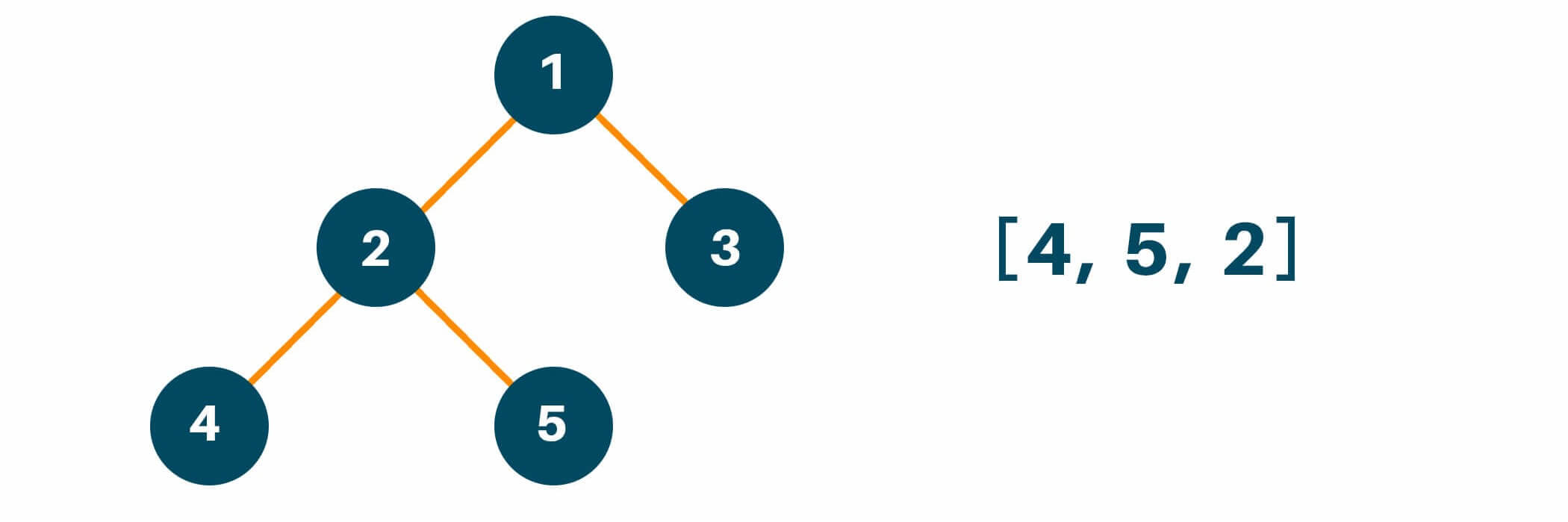
Later we will traverse the right subtree of the original tree similarly like we did with the left subtree and add the answer in the result array as shown below.

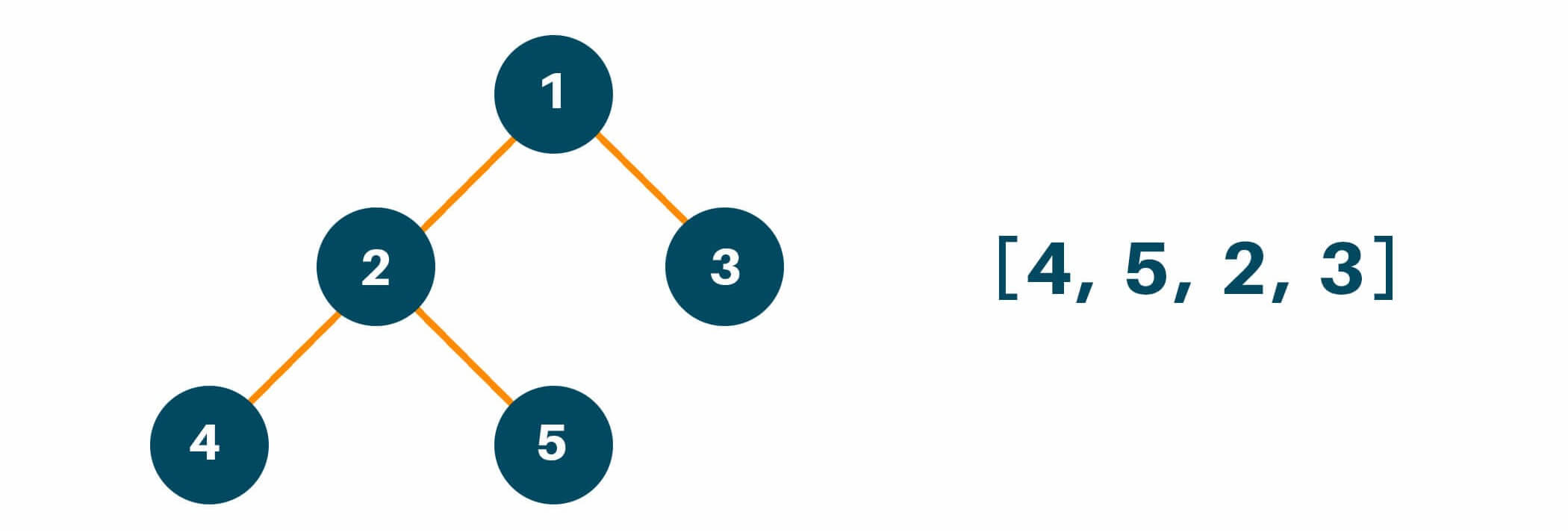
And lastly, we will traverse the root node of the original tree and finish our traversal method as shown in the figure below.

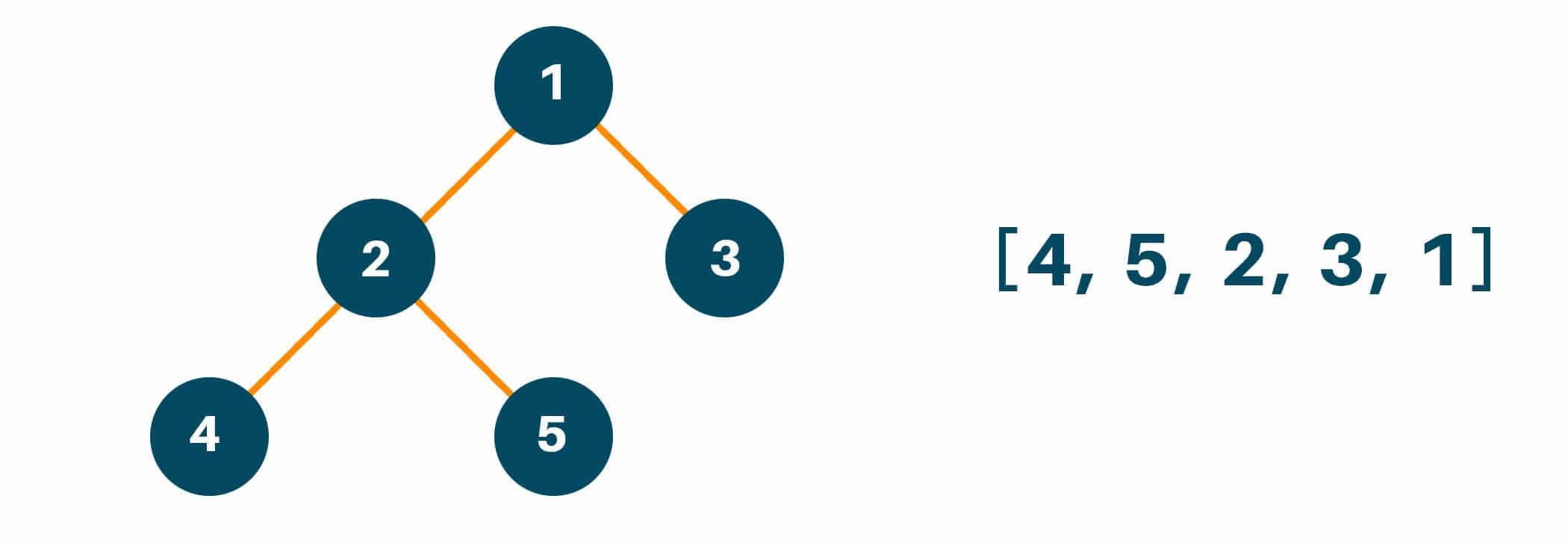
Python code for Postorder Tree Traversal with recursion

class TreeNode:

    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def postorderTraversal(root):
    answer = []

    postorderTraversalUtil(root, answer)
    return answer

def postorderTraversalUtil(root, answer):

    if root is None:
        return

    postorderTraversalUtil(root.left, answer)

    postorderTraversalUtil(root.right, answer)

    answer.append(root.val)

    return

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(postorderTraversal(root))

Output:

[4, 5, 2, 3, 1]

Time Complexity

Here, in tree traversal in python using recursion, the time complexity is O(n) where there are n nodes in the tree. While the space complexity is also O(n) for n nodes present in an answer array.

Application

1. Inorder traversal method is used for tree traversal to get the non-decreasing order of nodes.
2. The preorder traversal method is used to get the prefix expression of an expression tree. Also, preorder traversal helps to create a copy of the tree.
3. The postorder traversal method is used to get the postfix expression of an expression tree. Also, the postorder traversal method helps to delete the tree.

Conclusion

Hence, learning and understanding the application and usage of tree traversal in the real world proves that it is an important topic to study for any programmer. Therefore, in the above article, we studied the tree traversal in python using recursion and its methods of traversing with recursive nature. Also, we studied the python code for the tree traversal and its corresponding output.