A binary tree is a non-sequential data structure that stores huge data in a hierarchical manner and allows programmers to access it easily. Moreover, a binary tree is further divided into multiple categories such as a binary search tree, complete binary tree, etc. In this article, we will study one such category of the binary tree i.e., expression tree, and how to construct an expression tree with examples in detail. So, let's get started!
What is the Expression Tree?
An expression tree is one form of binary tree that is used to represent the expressions. A binary expression tree can represent two types of expressions i.e., algebraic expressions and Boolean expressions. Further, it can represent the expressions containing both, unary and binary operators.
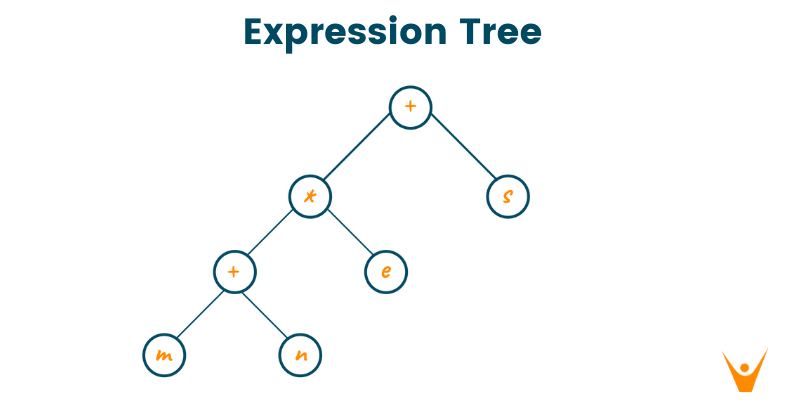
Just like a binary tree, an expression tree has zero, one, or two nodes for each parent node. The leaves of the expression tree are operands such as variable name or constants and the other nodes represents the operator of the expression. You can evaluate the expression tree by applying the operator at the root node with the values obtained by recursively evaluating the left and right subtree. The below image shows the expression tree for the equation: (m+n)*e+s
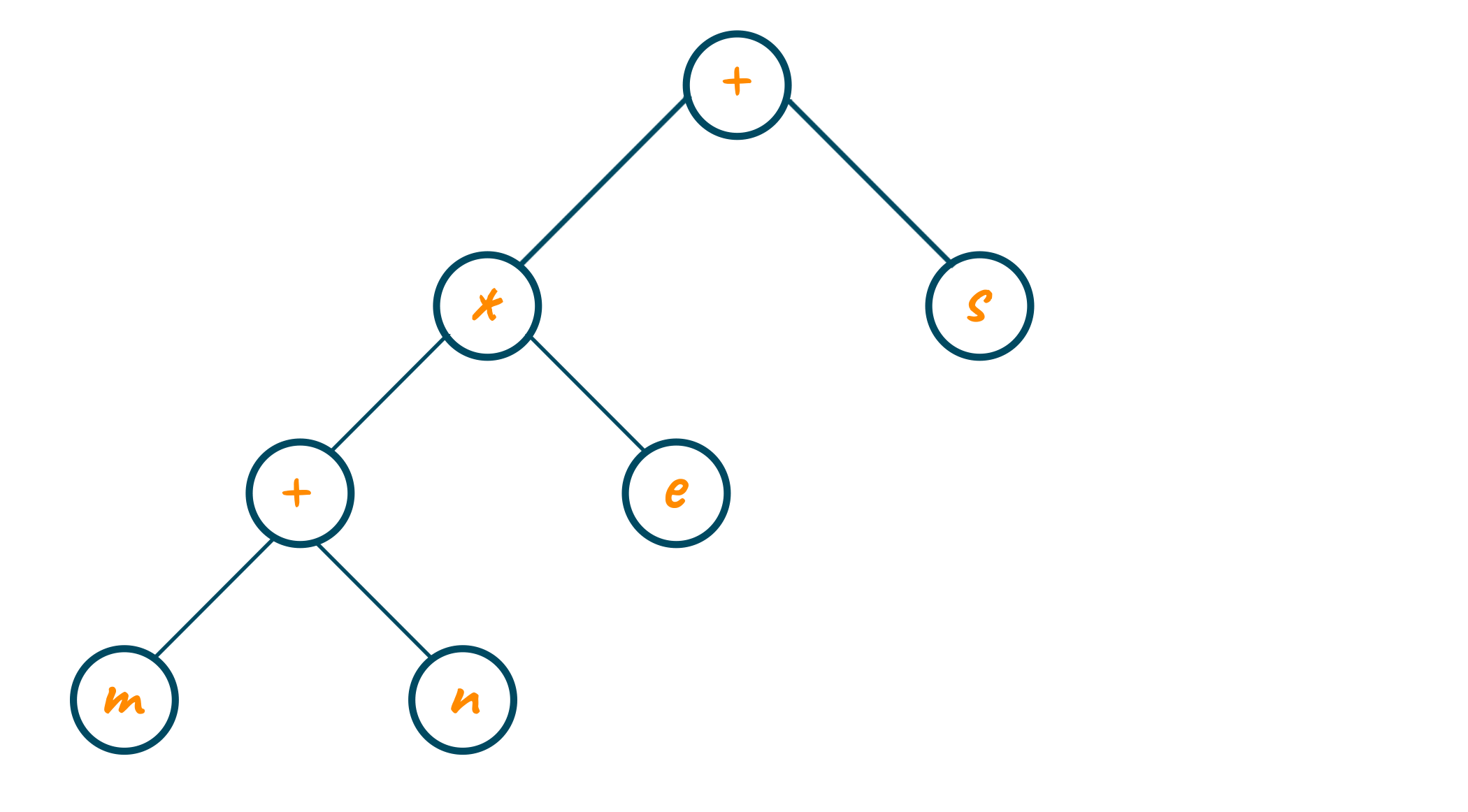
Evaluation of Expression Tree
You can easily form the algebraic expression using a binary expression tree by recursively calling the left subtree, then printing the root operator, and then recursively calling the right subtree. This strategy of calling left subtree, the root node, and right subtree are eventually called in order traversal method. Apart from this, you can also use the post-order traversal strategy where the left subtree is printed first, then the right subtree, and lastly the root node operator. As an alternative, you can also print the root node first and then recursively call left and right subtree respectively. This strategy is called pre-order traversal.
To learn more about tree traversal methods, visit our article “Level order traversal of the binary tree”.
Note that these tree depth-first traversal methods are standard representations of expression formats i.e., infix, postfix, and prefix expression. Let us study them in detail below:
Infix Expression
When you wish to print the infix expression, an opening and closing parenthesis must be added at the beginning and end of each expression. As each subtree of the expression tree represents the subexpression, you have to print the opening parenthesis at its start and closing parenthesis after iterating all of its children.
Pseudo Code
Algorithm infix (T) if (T not empty) if (T token is operator) print (open parenthesis) end if infix (T left-subtree) print (T token) infix (T right-subtree) if (T token is operator) print (close parenthesis) end if end if end infix
Postfix Expression
Every postfix expression is created by postorder traversal of the binary expression tree. Remember that it does not require any parenthesis, unlike infix expression.
Pseudo Code
Algorithm postfix (T) if (T not empty) postfix (T left-subtree) postfix (T right-subtree) print (T token) end if end postfix
Prefix Expression
Similar to postfix expression, prefix expression is also created by preorder traversal of the binary expression tree. Also, it does not require any parenthesis just like postfix expression. Check out the pseudo-code for prefix expression below
Pseudo Code
Algorithm prefix (T) if (T not empty) print (T token) prefix (T left subtree) prefix (T right subtree) end if end prefix
How to Construct an Expression Tree?
The best way to construct an expression tree is by reading the postfix expression symbol one at a time. We will also make use of the stack data structure here for storing the operators and operands while building a binary expression tree.
While traversing through postfix expression, if the symbol encountered is an operand, then its pointer is pushed into the stack. At the same time, if the symbol encountered is an operator, then the pointers of two one-node trees T1 and T2 storing the operands of the expressions are popped from the stack. Later, the new tree is formed with the root as the operator and left and right subtree as children pointers to T2 and T1 respectively. At last, the pointer to this new tree is pushed in the stack.
Pretty confusing right? Let’s understand it with an example.
Example
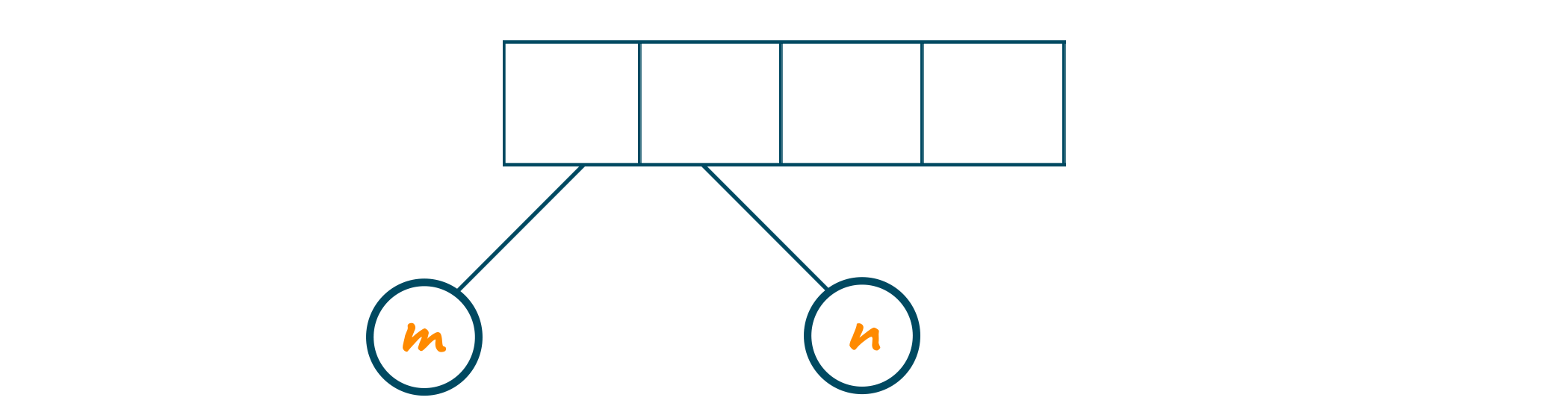
If the postfix notation is: m n * p q r + * +
Here the first two symbols are operands, i.e. m and n. So, the one-node tree is created as shown in the below image, and the pointers of these operands are pushed into the stack.
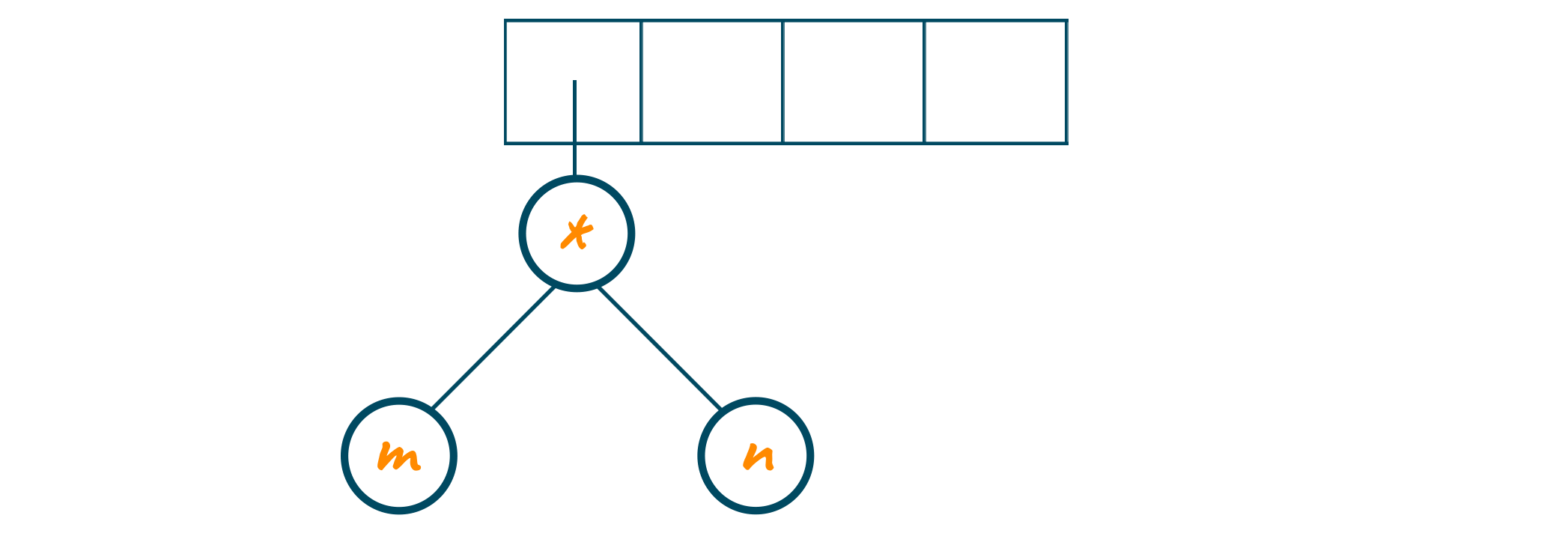
The next in the equation is the “*” operator. Therefore, we will pop the operands pointers from the stack and form a new tree where the operator serves as root node and operands serves as left and right child. Later, the pointer to the tree is pushed into the stack as shown in the below example.
Now, the postfix expression traverse to “p”, “q”, and “r”. As they are operands, the one-node tree is formed and the pointer to each node is pushed into the stack.
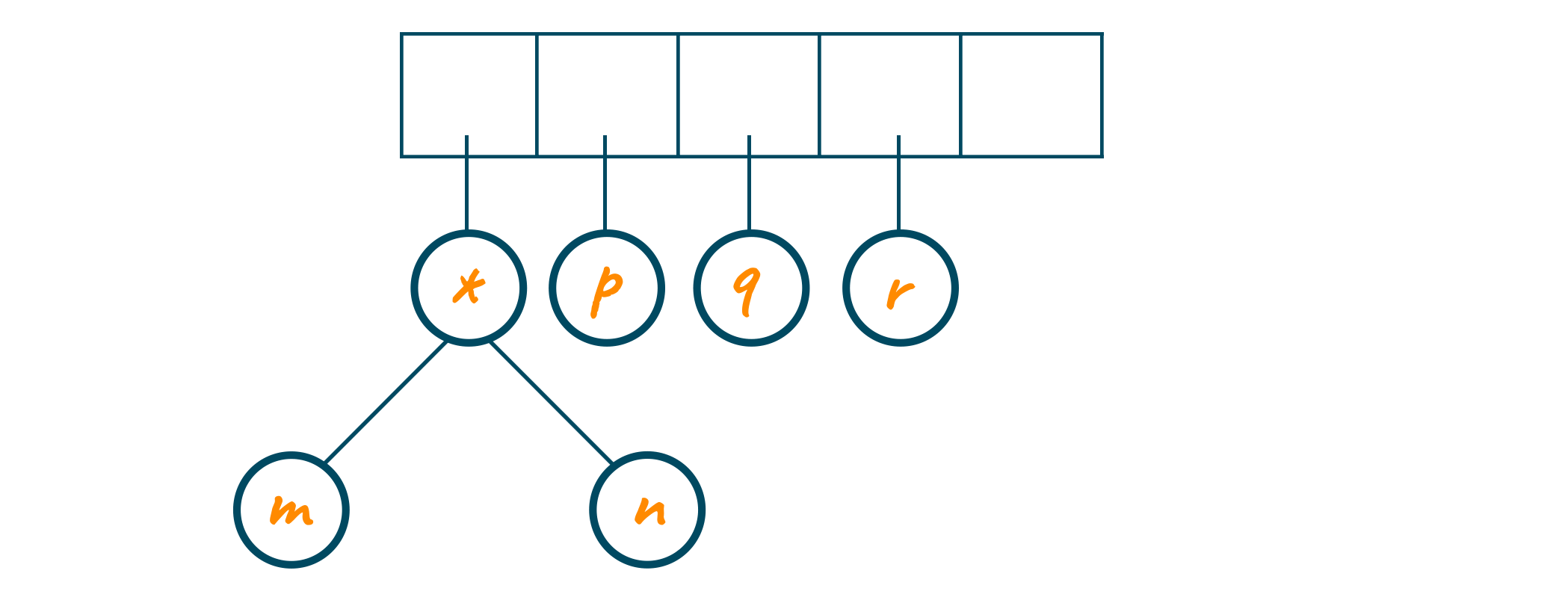
Later, the operator “+” is encountered and it serves as the root node to the last two one-node operands in the stack. The pointer to this new tree is stored in the stack as shown in the below image.
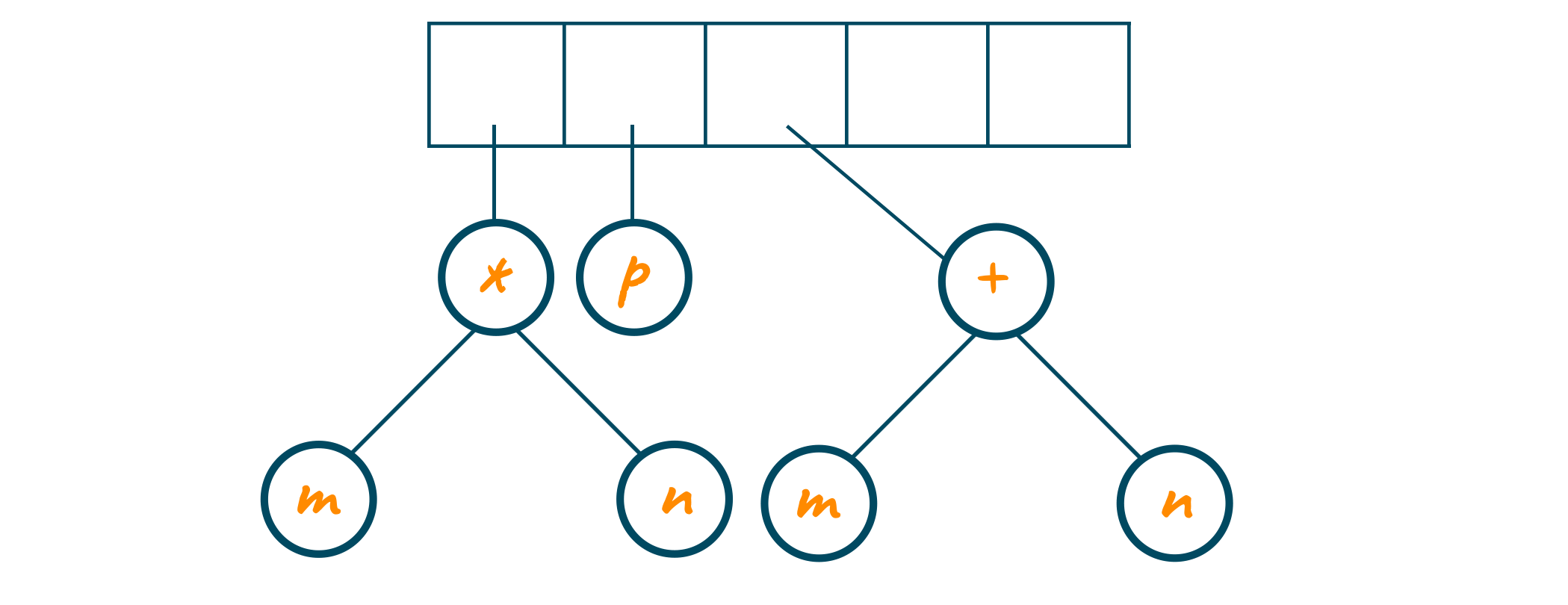
Now, again “*” operator is read . The last two tree pointers are popped from the stack and a new tree is built with root node as “*” operator as shown in the below image.
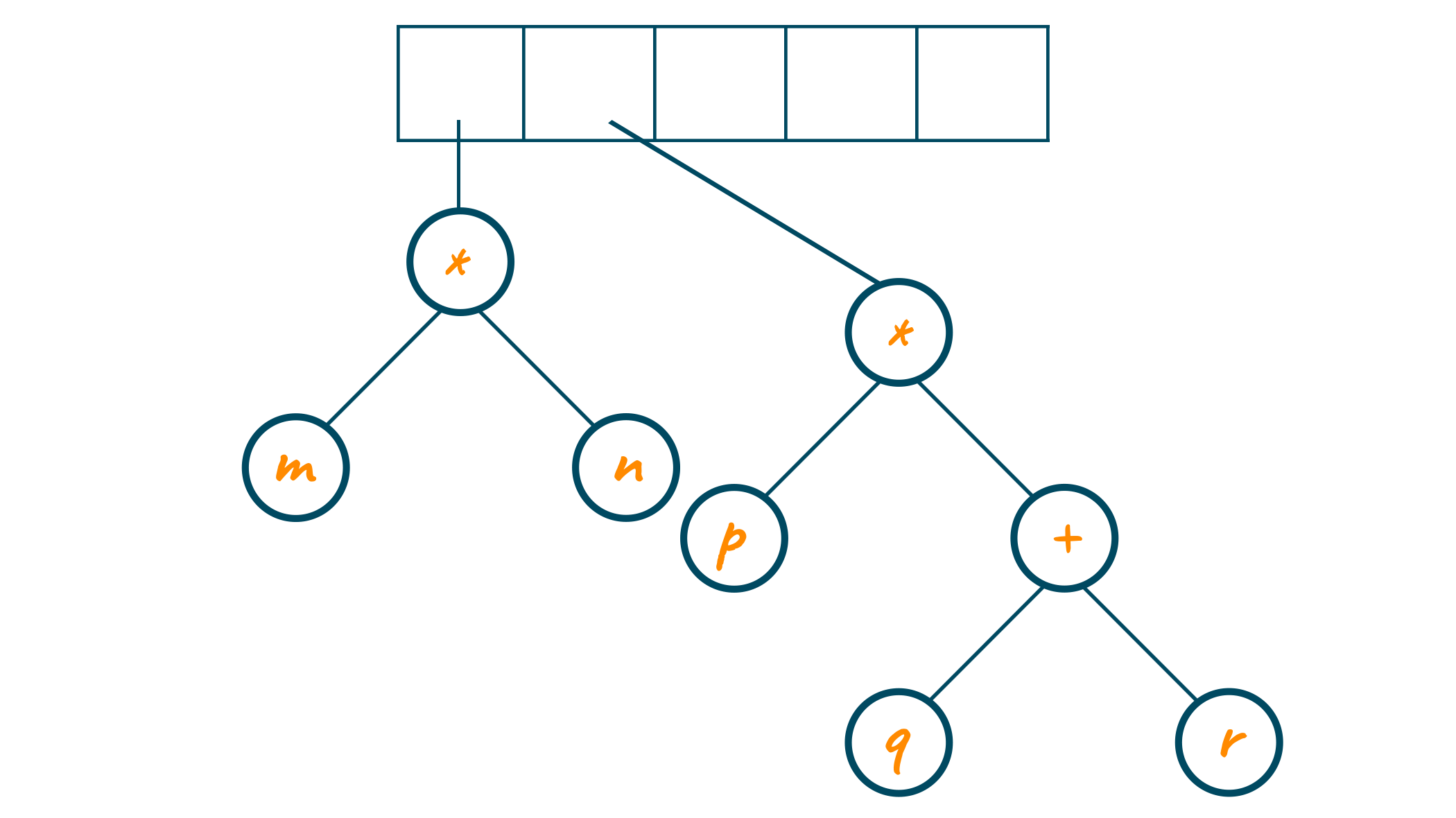
At last, the two individual trees are combined with the “+” operator, and the final expression tree is formed. The pointer to the new tree is stored in the stack as shown below.
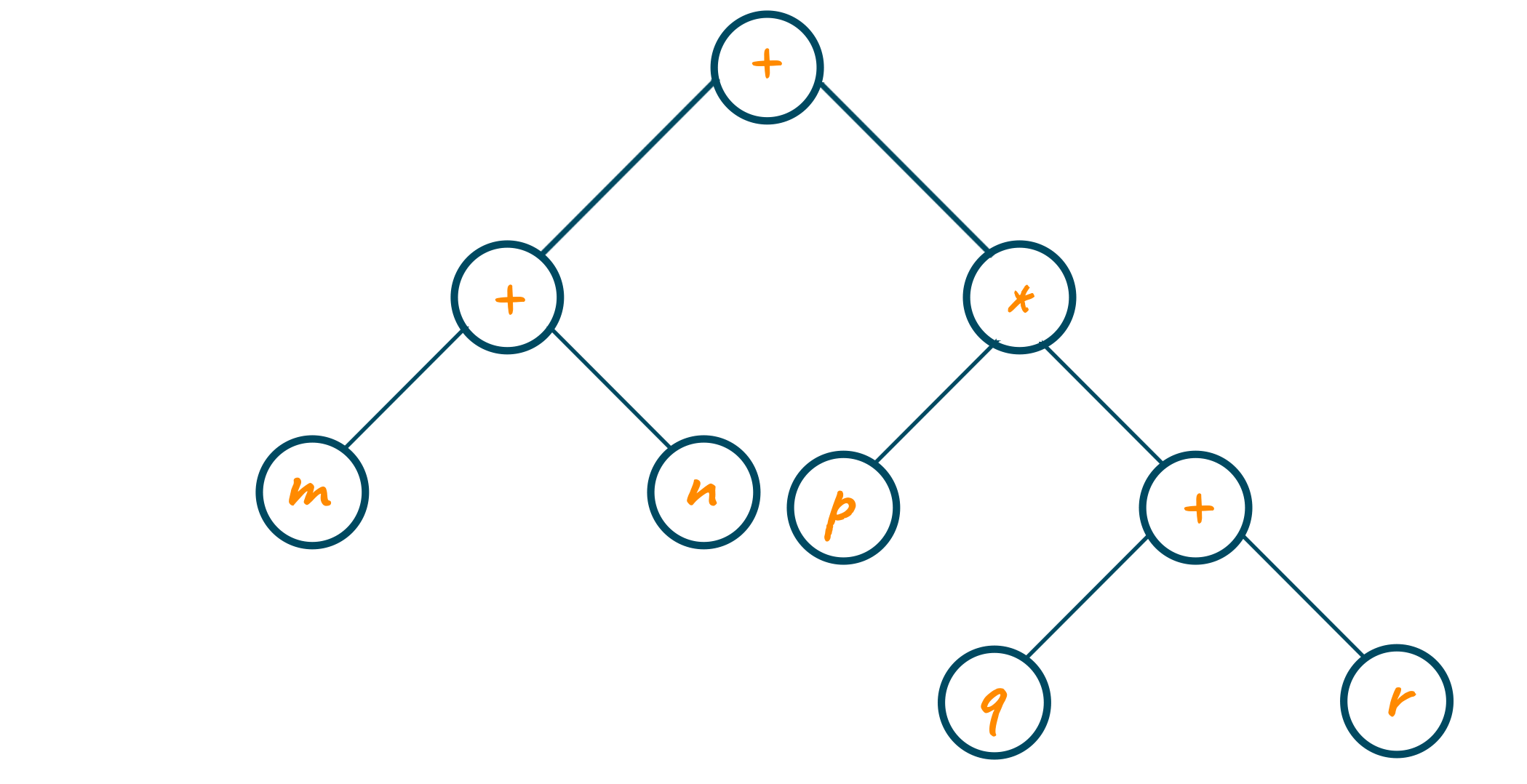
C++ Program for Construction of Expression Tree
#includeusing namespace std; // Tree Node Definition class TreeNode { public: char val; TreeNode *left, *right; TrreeNode() { this->left = NULL; this->right = NULL; } // Constructor Method TreeNode(char val) { this->val = val; this->left = NULL; this->right = NULL; } }; // Stack to hold the latest node class Stack { public: TreeNode *treeNode; Stack *next; // Constructor Method Stack(TreeNode *treeNode) { this->treeNode = treeNode; next = NULL; } }; class ExpressionTree { private: Stack *top; public: // Constructor Method ExpressionTree() { top = NULL; } // function to push a node in stack void push(TreeNode *ptr) { if (top == NULL) top = new Stack(ptr); else { Stack *nptr = new Stack(ptr); nptr->next = top; top = nptr; } } TreeNode *pop() { TreeNode *ptr = top->treeNode; top = top->next; return ptr; } TreeNode *peek() { return top->treeNode; } // function to insert character void insert(char val) { // If the encountered character is Number make a node an push it on stack if (isOperand(val)) { TreeNode *nptr = new TreeNode(val); push(nptr); } // else if it is operator then make a node and left and else if (isOperator(val)) { TreeNode *nptr = new TreeNode(val); nptr->left = pop(); nptr->right = pop(); push(nptr); } } // function to check if operand bool isOperand(char ch) { return ch >= '0' && ch <= '9' || ch>='A' && ch<='Z' || ch>='a' && ch<='z'; } // function to check if operator bool isOperator(char ch) { return ch == '+' || ch == '-' || ch == '*' || ch == '/'; } // function to construct expression Tree void construct(string eqn) { for (int i = eqn.length() - 1; i >= 0; i--) insert(eqn[i]); } void inOrder(TreeNode *ptr) { if (ptr != NULL) { inOrder(ptr->left); cout<<ptr->val; inOrder(ptr->right); } } }; int main() { string exp; ExpressionTree et; cout<<"Enter expression in Prefix form: "; cin>>exp; et.construct(exp); cout<<"In-order Traversal of Expression Tree : "; et.inOrder(et.peek()); return 0; };
Output
Input: +-abc
In-order Traversal of Expression Tree : a-b+c
Application of Expression Tree
- Expression trees enable the richer interaction with the function arguments
- It can be used to provide generic operators
- An expression tree is also used as the compiler
- It is used in dynamic LINQ sorting
- It is used as symbolic manipulators
- An expression tree is used as object cloning
Conclusion
Binary trees are widely accepted data structures by programmers irrespective of their domain language. It enables us to store a huge amount of non-linear data in an organized format and different methods to access it. An expression tree is one such variety of binary trees that helps us to analyze, modify and evaluate the complex algebraic and lambda expressions. It is highly recommended to learn and understand expression trees to make your programming easy and efficient.