In this vast technology-driven world, with information and data being the fuel, arranging the information into meaningful groups with certain purposes to fulfill is the ultimate motive. We all agree on the fact that managing information that is sorted is much easier than that which is unsorted.
In the world of programming, there are various types of sorting techniques like the bubble sort, counting sort, selection sort, etc. But, in today's tech blog, we're going to learn all about the Radix Sort, how it works, what its time and space complexity is, its codes in C++ & java, along with its applications.
What is a Radix Sort?
A Radix Sort is one of the many sorting techniques to arrange data in a particular fashion. In this type of sorting, we begin with the least significant digit and move toward the most significant digit while sorting the numbers.
Imagine how you were given roll numbers in your class. The teacher began to sort the students with their first letters in ascending order, then sort the second letter in ascending order, and so on. Take a look at the below illustration to gain a better understanding of this concept.
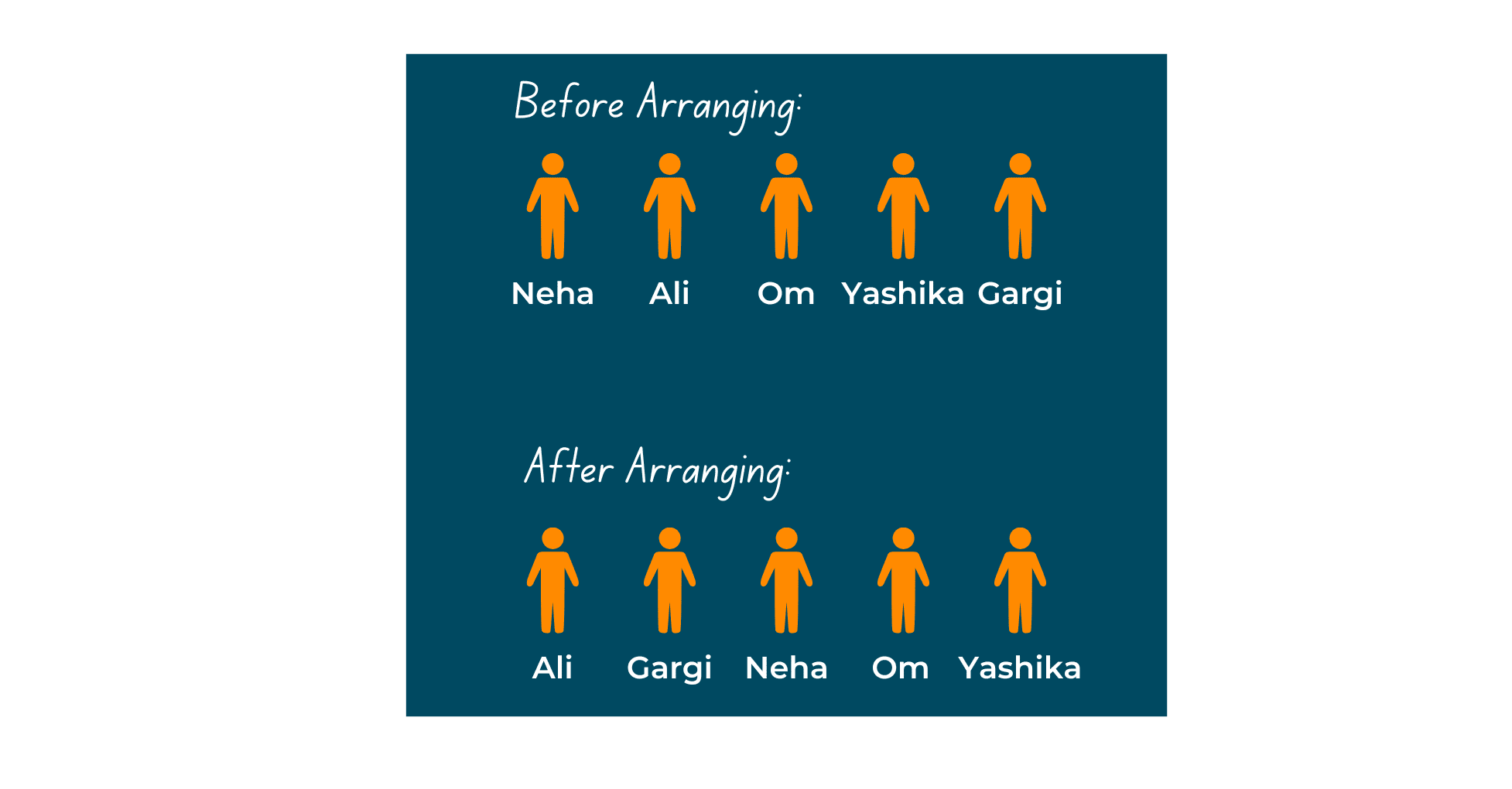
How does a Radix Sort work? (Algorithm)
In order to understand the implementation and algorithm of Radix Sort, you need to understand how it actually works in the system. So, let's discuss that. The following steps are taken to sort an array of elements with this technique.
- Get an array as input from the user.
- Start off by sorting the elements on basis of their unit place.
- Now, sort them on basis of their tense place.
- Keep sorting as per the number of digits in the highest number in the given array.
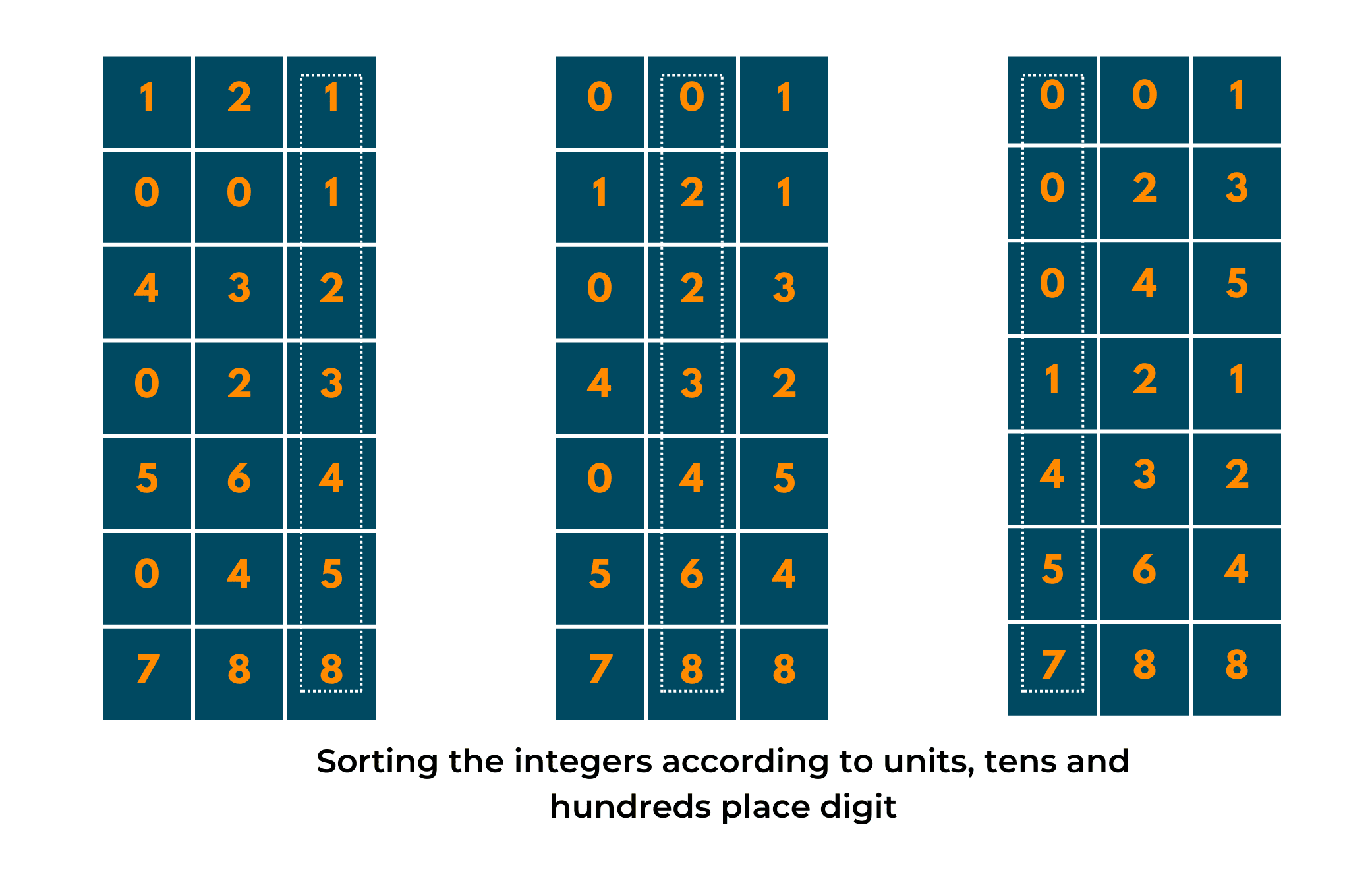
Take a look at the below image to understand sorting as per digit places.
Now, an example always makes the understanding much better. So, take a look below at the provided example and try to understand the steps and illustrations that follow.
Input: {121, 432, 564, 23, 1, 45, 788}
Output: {1, 23, 45, 121, 432, 564, 788}
Explanation:
1. We first find the largest number in the given array, which in this case, is 788. Now, calculate the number of digits in this number, 3. We did this because we have to sort all the numbers on the basis of their digits from least significant to most significant place.
NOTE: The number of digits in the largest array element is equal to the number of times we have to run the loop to sort the array.
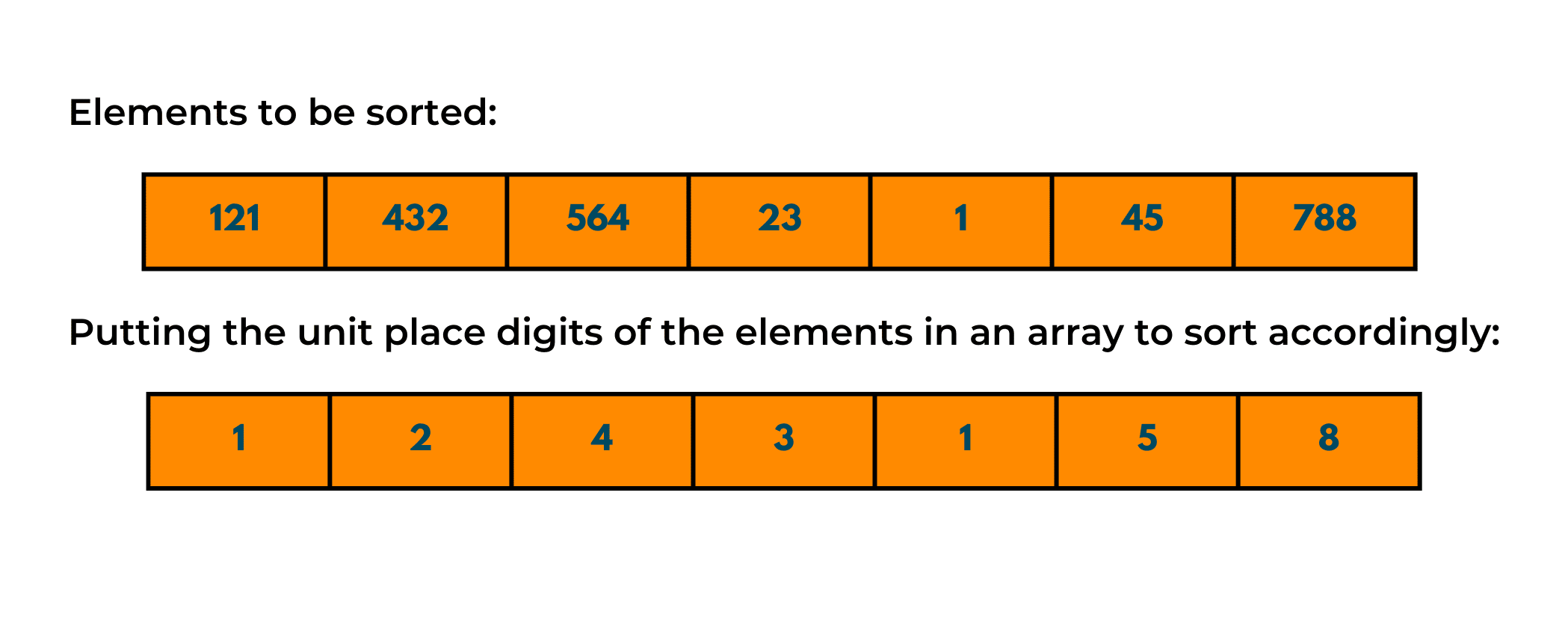
2. Now, using counting sort we'll sort the elements based on their unit place, as described in the image below.

3. Moving on, we'll now sort elements based on their tens place.

4. Finally, we'll now sort them on their hundreds place basis and Voila! you've got the set of sorted array elements.

Implementation of Radix Sort in C++
Here is the C++ code for Radix Sort:
#include using namespace std; // Function to get the largest element from an array int getMax(int array[], int n) { int maximum = array[0]; for (int i = 1; i < n; i++) if (array[i] > maximum) maximum = array[i]; return maximum; } // Using counting sort to sort the elements on digit basis void countingSort(int array[], int size, int place) { const int max = 10; int output[size]; int count[max]; for (int i = 0; i < max; ++i) count[i] = 0; // Calculate number of elements for (int i = 0; i < size; i++) count[(array[i] / place) % 10]++; // Calculate cumulative count for (int i = 1; i < max; i++) count[i] += count[i - 1]; // Place the elements in sorted order for (int i = size - 1; i >= 0; i--) { output[count[(array[i] / place) % 10] - 1] = array[i]; count[(array[i] / place) % 10]--; } for (int i = 0; i < size; i++) array[i] = output[i]; } // Main function to implement radix sort void RadixSort(int array[], int size) { // Get maximum element int max = getMax(array, size); // Apply counting sort to sort elements based on place value. for (int place = 1; max / place > 0; place *= 10) countingSort(array, size, place); } // Print an array void printArray(int array[], int size) { int i; for (i = 0; i < size; i++) cout << array[i] << " "; cout << endl; } // Driver code int main() { int array[] = {121, 432, 564, 23, 1, 45, 788}; int n = sizeof(array) / sizeof(array[0]); RadixSort(array, n); printArray(array, n); }
Implementation of Radix Sort in Java
Here is the Java code for Radix Sort:
import java.util.Arrays; class RadixSort { // Using counting sort to sort the elements in the basis of significant places void countingSort(int array[], int size, int place) { int[] output = new int[size + 1]; int max = array[0]; for (int i = 1; i < size; i++) { if (array[i] > max) max = array[i]; } int[] count = new int[max + 1]; for (int i = 0; i < max; ++i) count[i] = 0; // Calculate count of elements for (int i = 0; i < size; i++) count[(array[i] / place) % 10]++; // Calculate cumulative count for (int i = 1; i < 10; i++) count[i] += count[i - 1]; // Place the elements in sorted order for (int i = size - 1; i >= 0; i--) { output[count[(array[i] / place) % 10] - 1] = array[i]; count[(array[i] / place) % 10]--; } for (int i = 0; i < size; i++) array[i] = output[i]; } // Function to get the largest element from an array int getMax(int array[], int n) { int max = array[0]; for (int i = 1; i < n; i++) if (array[i] > max) max = array[i]; return max; } // Main function to implement radix sort void radixSort(int array[], int size) { // Get maximum element int max = getMax(array, size); // Apply counting sort to sort elements based on place value. for (int place = 1; max / place > 0; place *= 10) countingSort(array, size, place); } // Main function public static void main(String args[]) { int[] data = { 121, 432, 564, 23, 1, 45, 788 }; int size = data.length; RadixSort rs = new RadixSort(); rs.radixSort(data, size); System.out.println("Sorted Array: "); System.out.println(Arrays.toString(data)); } }
Output:
Sorted Array: {1, 23, 45, 121, 432, 564, 788}
The Java code might be a bit more complex. You can get connect with our Java Tutors for instant help right now.
Time Complexity of Radix Sort
Time complexities for radix sort are mentioned in below table:
| Best | O(n+k) |
| Worst | O(n+k) |
| Average | O(n+k) |
Space Complexity of Radix Sort
Space complexities for radix sort are mentioned in below table:
| Space Complexity | O(max) |
| Stability | Yes |
Applications of Radix Sort
Radix Sort is generally executed and used in the below scenarios:
- when there are many numbers to sort
- DC3 algorithm while making the suffix array
Conclusion
Sorting is an important concept to learn while understanding and implementing various coding techniques. Although many sorting methods are available like counting sort, radix sort, bubble sort, etc each one has its own application in different fields. So, keep practicing such concepts and clear your doubts with the 24*7 doubt-clearing sessions with FavTutor experts.








