Prim's Algorithm in C++ to Find Minimum Spanning Tree

There are several algorithms for finding the minimum spanning tree of a graph, such as Kruskal's algorithm and Prim's algorithm. These algorithms are based on the principle of greediness and guarantee finding the minimum spanning tree of a graph in an efficient way. In this article, we will study what Prim's Algorithm is, and its implementation in C++.

But first, we must revise our understanding of a minimum spanning tree.

What is a Minimum Spanning Tree?

A minimum spanning tree, or MST, is a subset of the edges of a weighted undirected graph that connects all the vertices together without any cycles and has the minimum possible total edge weight. 

An MST has several important properties. Firstly, it is a tree, meaning that it does not contain any cycles. Secondly, it is a spanning tree, meaning that it connects all vertices of the graph. Finally, it is minimum, meaning that it has the smallest possible total edge weight among all the possible spanning trees of the graph.

Prim's Algorithm

Prim's algorithm is used to find the minimum spanning tree of a weighted undirected graph. The algorithm works by starting at a single vertex and gradually building up the spanning tree by adding edges one at a time. At each step, it selects the edge with the smallest weight that connects a vertex in the tree to a vertex outside the tree. This process is repeated until all vertices are included in the tree.

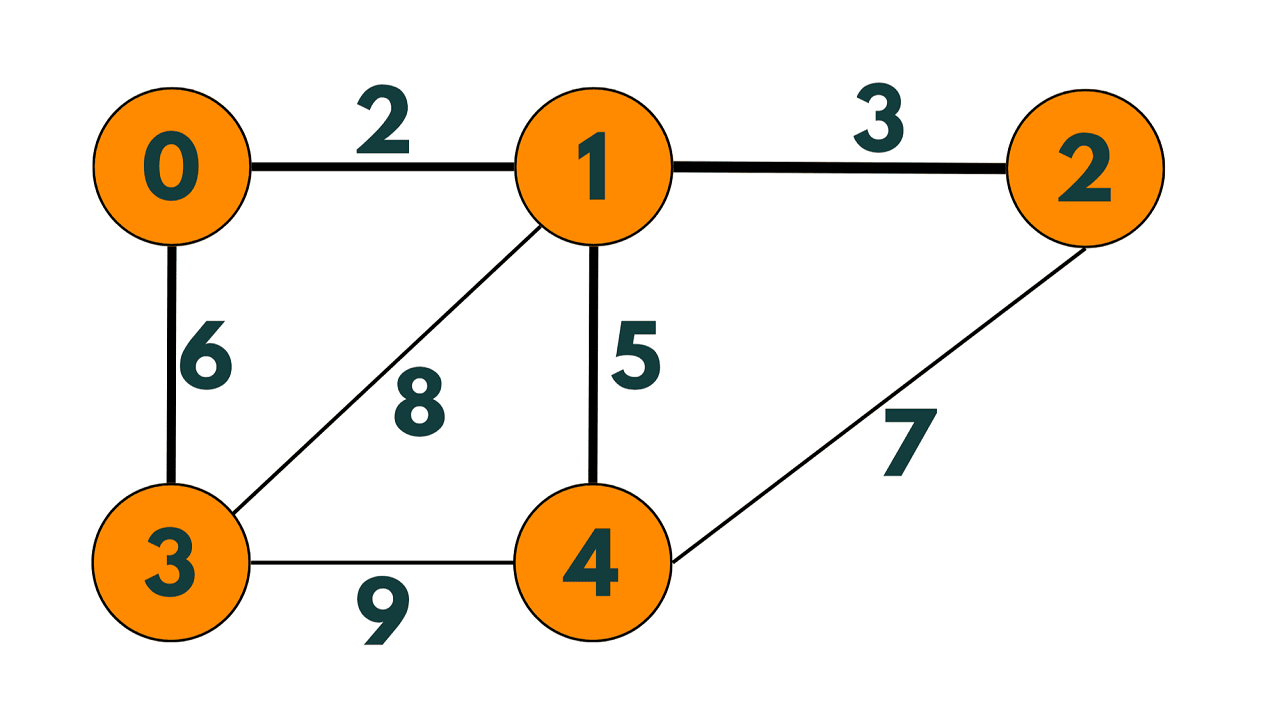
Let's illustrate this algorithm with an example. Consider the following graph:

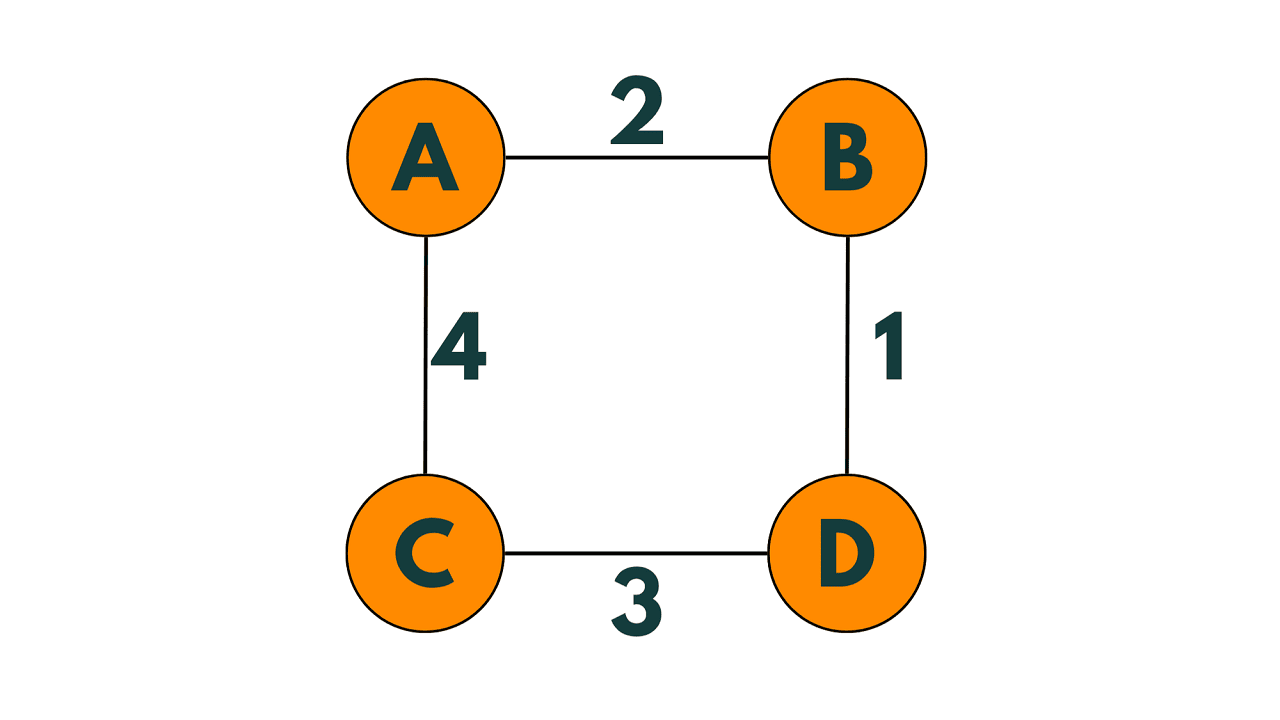
We start with the vertex A.

We initialize the set T with only A.

We initialize the priority queue Q with all the edges connected to A, sorted by weight:

(A, B) with weight 2

(A, C) with weight 4

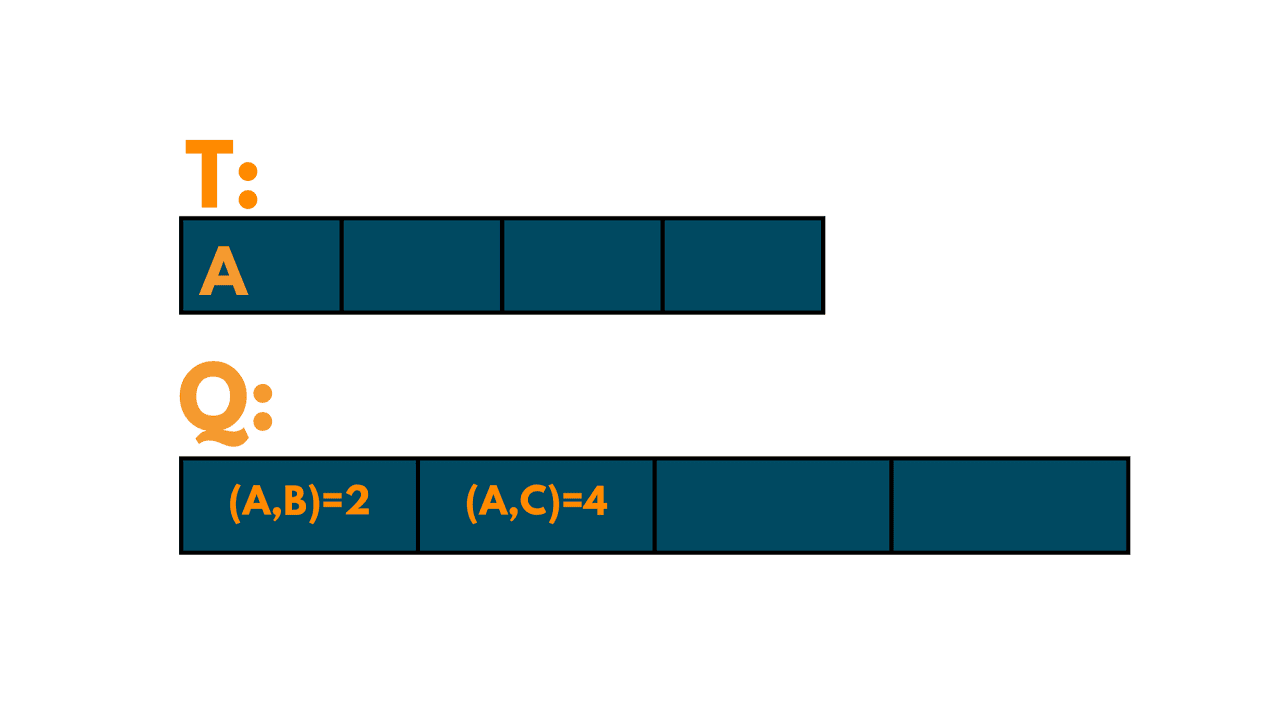
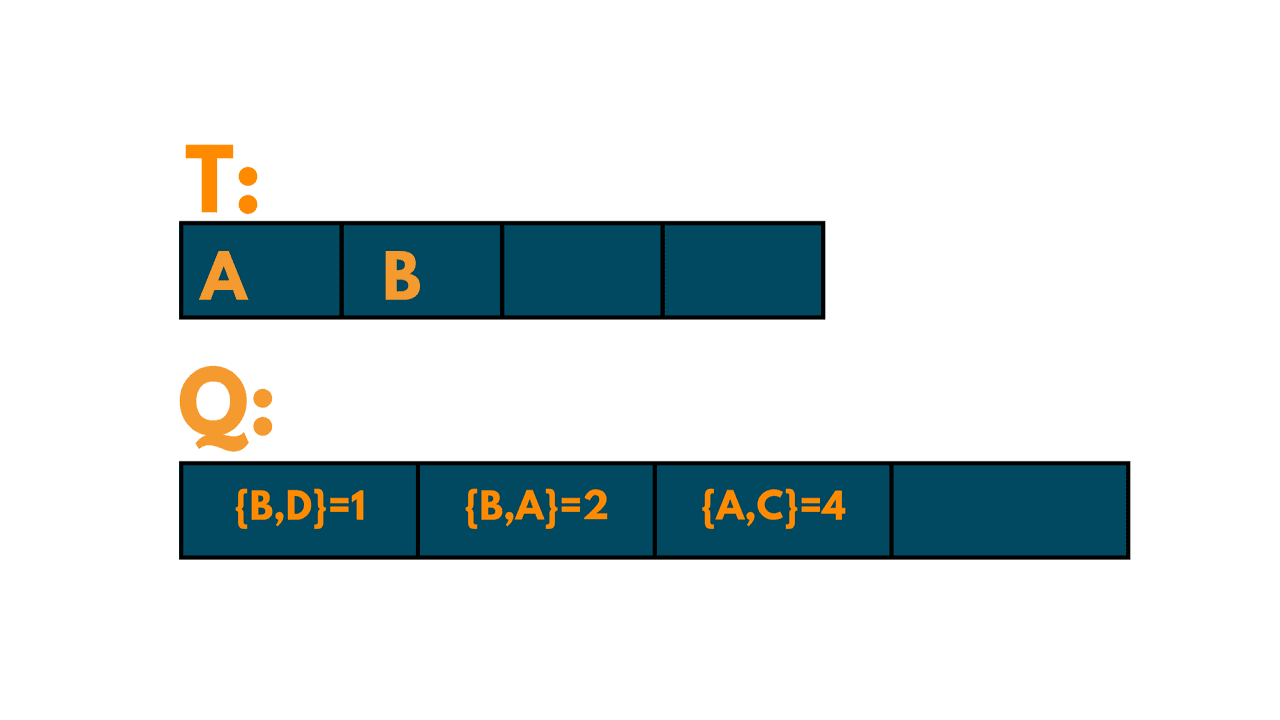
We remove the edge (A, B) from Q and add it to T. The set T is now {A, B}.

We add all the edges connected to B to Q:

(B, A) with weight 2

(B, D) with weight 1

We remove the edge (B, D) from Q and add it to T. The set T is now {A, B, D}.

We add all the edges connected to D to Q:

(D, B) with weight 1

(D, C) with weight 3

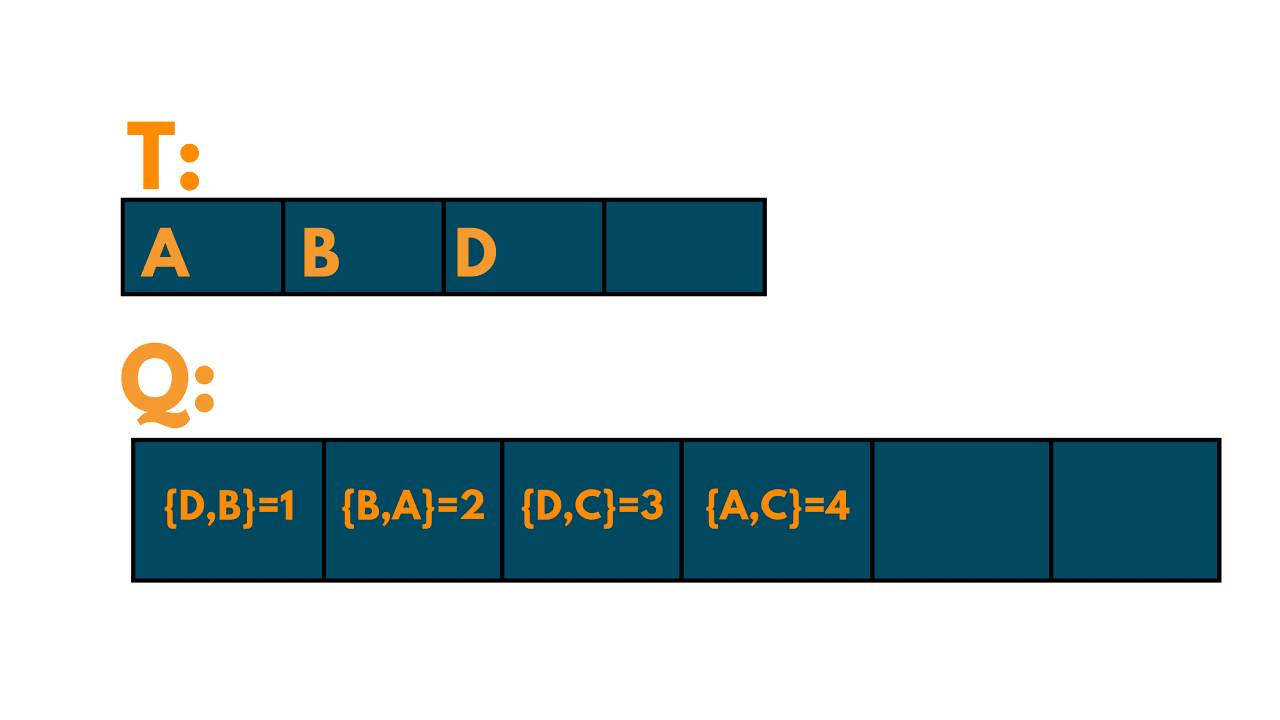
We remove the edge (D, B) from Q because B is already in T.

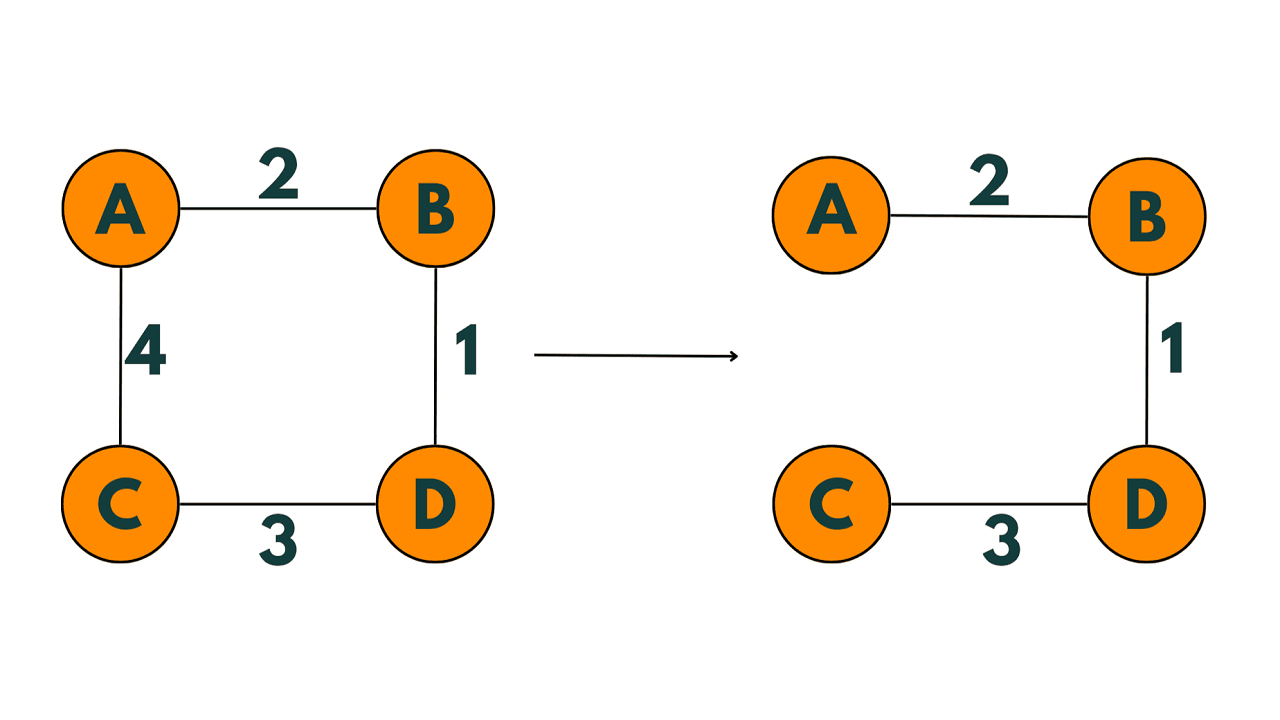
We remove the edge (D, C) from Q and add it to T. The set T is now {A, B, D, C}.

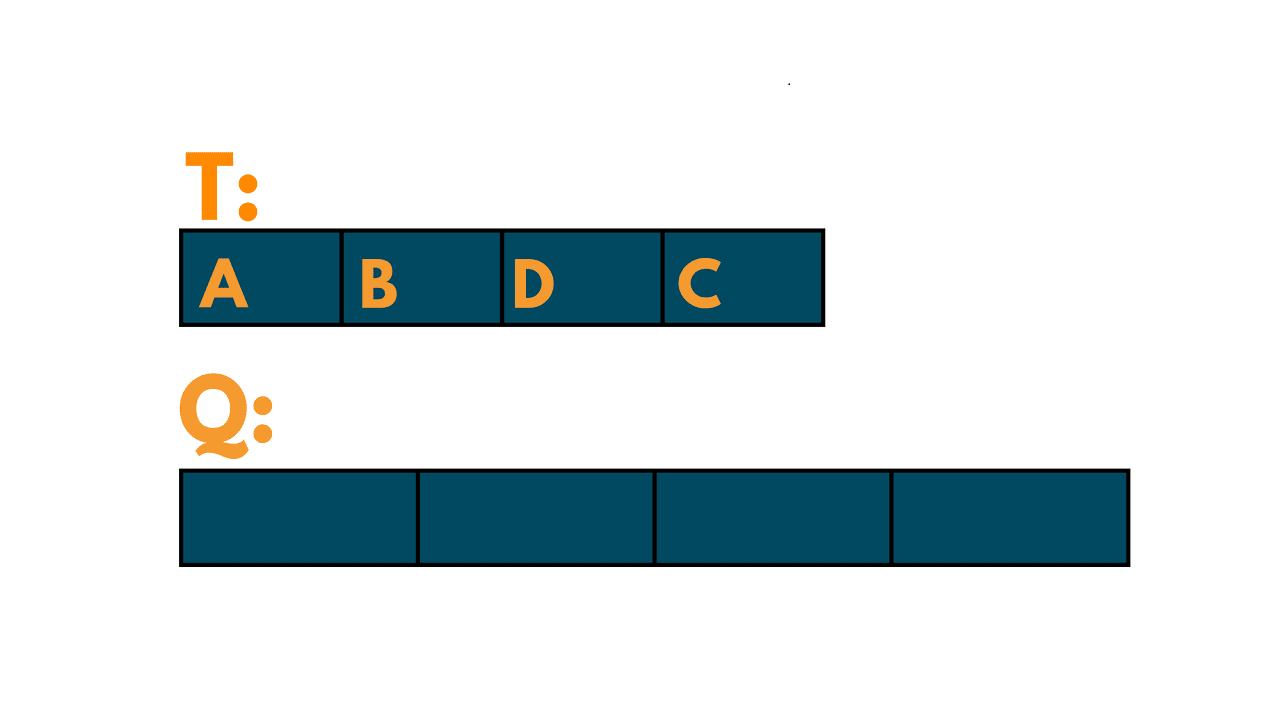
We have now included all the vertices in the tree, so we stop. The minimum spanning tree of the graph is shown below:

Here's a step-by-step breakdown of Prim's algorithm:

1. Choose an arbitrary vertex to start the tree.
2. Initialize a set T containing only the starting vertex. This set will eventually contain the minimum spanning tree.
3. Initialize a priority queue Q containing all the edges connected to the starting vertex, sorted by their weight.
4. While Q is not empty:
   1. Remove the edge with the smallest weight from Q.
   2. If the edge connects a vertex in T to a vertex, not in T, add the edge to T and add all the edges connected to the new vertex to Q.

Prim's Algorithm in C++

Here is the complete C++ program to implement Prim's Algo:

#include <bits/stdc++.h>
using namespace std;

#define INF 1e9

typedef pair<int, int> pii;

vector<vector<pii>> adj; // adjacency list of the graph
vector<bool> visited; // visited array to keep track of visited vertices

int prim(int start) {
    int n = adj.size();
    int mstWeight = 0;
    priority_queue<pii, vector<pii>, greater<pii>> pq; // priority queue to select the next edge to add to the MST

    pq.push(make_pair(0, start)); // start from the given vertex with weight 0

    while (!pq.empty()) {
        int u = pq.top().second;
        int w = pq.top().first;
        pq.pop();

        if (visited[u]) continue; // skip visited vertices
        visited[u] = true;
        mstWeight += w;

        for (auto& v : adj[u]) {
            if (!visited[v.first]) {
                pq.push(make_pair(v.second, v.first)); // add edges connected to the current vertex
            }
        }
    }

    return mstWeight;
}

int main() {
    // define the graph
    adj.resize(5); // 5 vertices

    // add edges to the graph
    adj[0].push_back(make_pair(1, 2)); // edge from vertex 0 to 1 with weight 2
    adj[1].push_back(make_pair(0, 2)); // edge from vertex 1 to 0 with weight 2

    adj[0].push_back(make_pair(3, 6)); // edge from vertex 0 to 3 with weight 6
    adj[3].push_back(make_pair(0, 6)); // edge from vertex 3 to 0 with weight 6

    adj[1].push_back(make_pair(2, 3)); // edge from vertex 1 to 2 with weight 3
    adj[2].push_back(make_pair(1, 3)); // edge from vertex 2 to 1 with weight 3

    adj[1].push_back(make_pair(3, 8)); // edge from vertex 1 to 3 with weight 8
    adj[3].push_back(make_pair(1, 8)); // edge from vertex 3 to 1 with weight 8

    adj[1].push_back(make_pair(4, 5)); // edge from vertex 1 to 4 with weight 5
    adj[4].push_back(make_pair(1, 5)); // edge from vertex 4 to 1 with weight 5

    adj[2].push_back(make_pair(4, 7)); // edge from vertex 2 to 4 with weight 7
    adj[4].push_back(make_pair(2, 7)); // edge from vertex 4 to 2 with weight 7

    adj[3].push_back(make_pair(4, 9)); // edge from vertex 3 to 4 with weight 9
    adj[4].push_back(make_pair(3, 9)); // edge from vertex 4 to 3 with weight 9

    visited.resize(5, false); // set all vertices as unvisited

    int mstWeight = prim(0); // find the MST starting from vertex 0

    cout << "Minimum spanning tree weight: " << mstWeight << endl;

    return 0;
}

Output:

Minimum spanning tree weight: 16

Time and Space complexity

The priority queue used to store the edges has a maximum size of the number of edges in the graph, which is O(E), where E is the number of edges. Each edge is added and removed from the priority queue once, which takes O(log E) time. Additionally, each vertex is visited once, and for each vertex, its adjacent edges are processed, which takes O(E) time in total.

Therefore, the time complexity of Prim's algorithm is O(E log E) + O(E) = O(E log E). The space complexity of Prim's algorithm is O(E + V).

Note that if the graph is dense, i.e., if E is close to V^2, then the time complexity of Prim's algorithm is dominated by the O(E^2) time required to build the adjacency list representation of the graph, and the O(E) space required to store the adjacency list becomes the dominant term in the space complexity. In this case, using a different algorithm, such as Kruskal's algorithm, may be more efficient.

Advantages and Disadvantages

The main use of Prim's algorithm is to find the minimum spanning tree for a connected weighted undirected graph. It guarantees that the MST found is optimal (i.e., has the minimum total weight) and works well on dense graphs, where the number of edges is close to V^2.

But note that it only works on connected graphs, so disconnected graphs need to be handled separately. Also, it may not work well on sparse graphs, where the number of edges is much smaller than V^2, as the time and space complexity may become dominated by the cost of building the adjacency list representation of the graph.

Real-World Applications

Prim's algorithm, being a minimum spanning tree algorithm, is useful in various applications in computer science and beyond. Some of the common applications of Prim's algorithm are:

• Network design: Prim's algorithm is commonly used in designing communication networks such as telephone networks, internet routing, and cable television networks. The algorithm helps to find the minimum cost connections between nodes in a network.

• Image segmentation: In image processing, it can be used to segment an image into connected components based on the similarity of pixel intensities.

• Clustering: The algorithm can be used for clustering data in machine learning and data analysis. By using the minimum spanning tree of a graph, data can be grouped into clusters based on the distances between the data points.

• Circuit design: Prim's algorithm is used in circuit design to find the minimum cost connections between circuit components.

Conclusion

In summary, Prim's algorithm has a wide range of applications in various fields due to its ability to find the minimum spanning tree of a graph. Its simplicity and efficiency make it a popular choice in many areas where optimization problems need to be solved.