Graphs might just be one of the most difficult areas of programming to approach as a beginner. One of the most popular algorithms used with graphs is the one for traversing the graph in the minimum time possible as well as the one which produces a minimum spanning tree from it. For that, we use Kruskal's Algorithm, which we will learn in this article, along with its implementation in C++.
What is Kruskal’s Algorithm?
For graph traversal, we have the BFS and DFS algorithms, while the equivalent minimum spanning tree can be produced with the help of Prim’s algorithm or Kruskal’s algorithm. These are some of the easiest algorithms that one can learn when they have to use graphs to solve coding problems.
The main objective of using Kruskal’s algorithm is for getting the minimum cost-spanning tree for a graph. Minimum-spanning trees help reduce the number of edges to a large extent so that only the minimal edges are shown. This, in turn, finds application in solving a variety of questions that can be solved using graphs.
However, this makes no sense if you don’t understand what a minimum spanning tree exactly is. This can be the best explanation with an example.
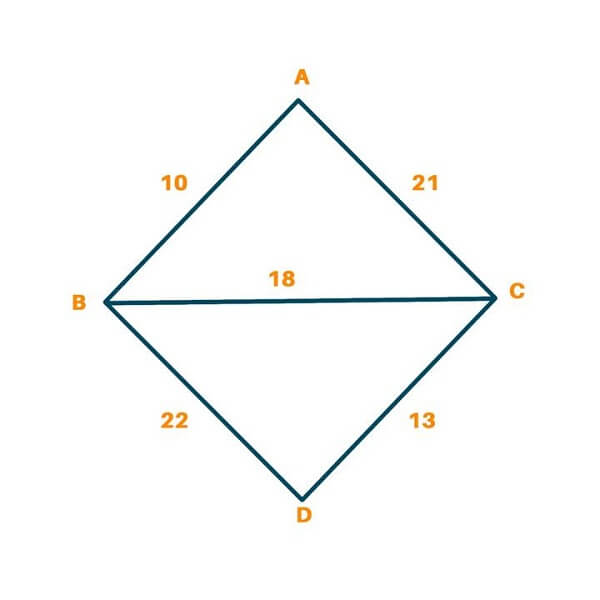
Let us suppose we have a graph like this:
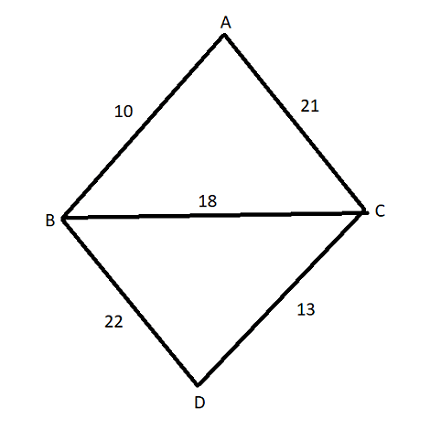
We have four nodes, A, B, C, and D. We can rearrange the various edges of the graph to remove cycles and form a tree. This can be done in several ways:-
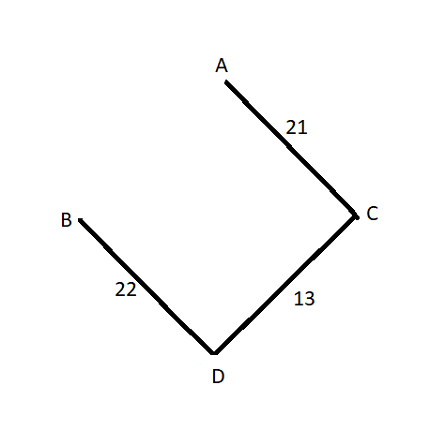
In this case, the weight of the tree is 22+21+13=56.
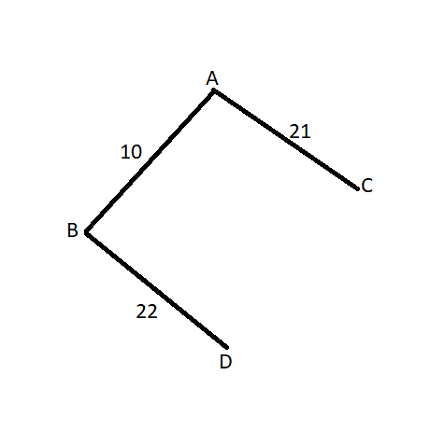
In this case, the weight of the tree is 10+22+21=53.
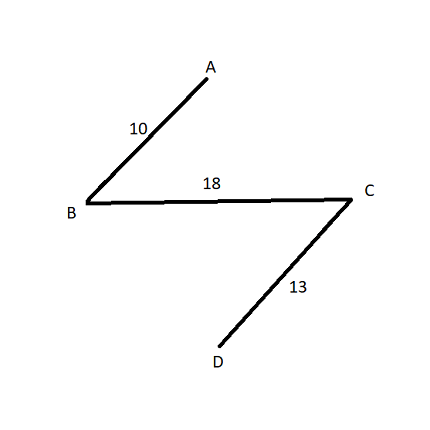
In this case, the weight of the tree is 10+18+13=41. On carefully comparing, we might see that this tree has the minimum weight among all of the trees obtained. The main objective of Prim’s algorithm or Kruskal’s algorithm is to obtain this minimum spanning tree. A tree obtained from a graph such that the sum of the weights of the edges is minimum is called a minimum spanning tree.
How does Kruskal Algorithm work?
The algorithm starts with V in different groups (where V is the number of vertices in a graph). At every step of the process, the edge with the minimum weight of the graph is chosen and added to the minimum spanning tree.
An edge is only chosen in such a way if it does not create a cycle; if the edge with the minimum weight causes a cycle in the minimum spanning tree, the algorithm proceeds with the edge with the second minimum weight.
Adding an edge to the graph also merges both of the vertices making it into one group (remember that each of the vertices starts in separate groups initially). When the algorithm is finished, only one group is left which represents the minimum spanning tree.
C++ Kruskal’s algorithm works in a slightly different manner than Prim’s algorithm. Prim’s algorithm pushes vertices to this group and expands it one by one starting from the two vertices which form the edge with the minimum weight.
Kruskal’s algorithm is more concerned with the edges rather than the vertices and deals with edges directly by adding their vertices to a common group.
There are two main ways of implementing Kruskal’s algorithm in C++: disjoint sets or priority queues. Using disjoint sets is slightly better as it helps visualize the change in the groups at any point in time.
The algorithm is as follows:
- Initialize an array for storing the groups of the vertices.
- Initialize an array for storing the edges of the graph with their weights.
- Initialize the spanning tree as an empty array.
- Put all vertices of the graph into different groups.
- Sort the array of edges in increasing order of weights.
- Continue step 7 till there is no more edge remaining in the sorted array of edges
- If the group of one node of an edge does not match the group of the other node of the edge, add them both to the same group and add the edge to the spanning tree array.
- Iterate through the spanning-tree array and add the weights of the edges.
- The sum of the edges thus obtained is the weight of the minimum spanning tree, while the spanning tree array contains the edges for the same.
Let’s work out an example. Consider the above graph and let’s try to apply Kruskal’s algorithm to it.
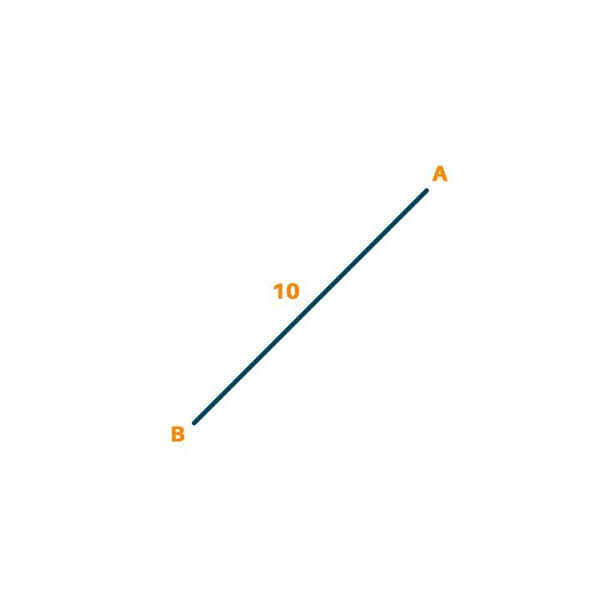
Initially, we have to pick the first edge which has the minimum weight. AB is picked here, which weighs 10.
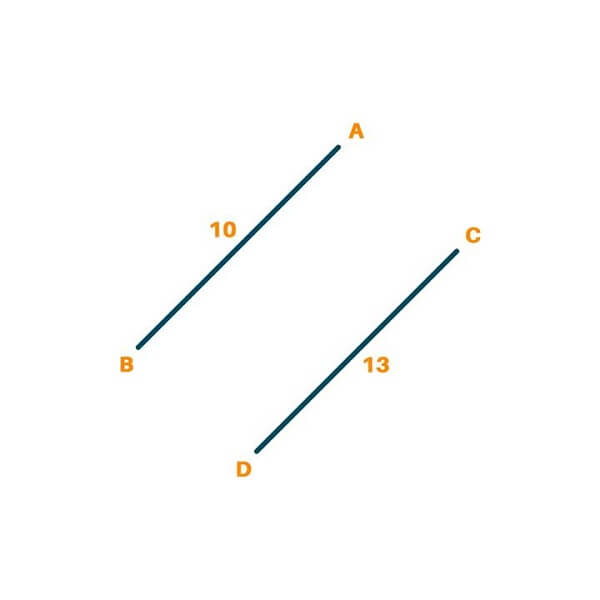
Now, we pick the edge with the second minimum weight. The CD is picked here since it weighs 13.
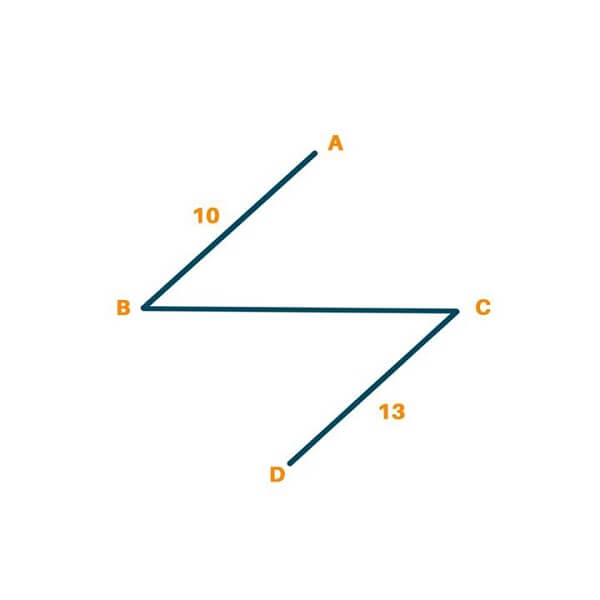
Proceeding further, we find that the edge with minimum weight is BC. The weight of this edge is 18.
Since a complete tree is obtained, we stop the algorithm here. The minimum weight for the tree thus obtained is 10+18+13=41.
C++ Program for Kruskal's Algorithm
The C++ implementation of Kruskal’s algorithm with the help of the union-find algorithm is given below. This is the source code of the C++ Krushkal Algorithm:-
#include <iostream> #include <vector> #include <algorithm> using namespace std; const int MAX = 1e6-1; int root[MAX]; const int nodes = 4, edges = 5; pair <long long, pair<int, int> > p[MAX]; int parent(int a) //find the parent of the given node { while(root[a] != a) { root[a] = root[root[a]]; a = root[a]; } return a; } void union_find(int a, int b) //check if the given two vertices are in the same “union” or not { int d = parent(a); int e = parent(b); root[d] = root[e]; } long long kruskal() { int a, b; long long cost, minCost = 0; for(int i = 0 ; i < edges ; ++i) { a = p[i].second.first; b = p[i].second.second; cost = p[i].first; if(parent(a) != parent(b)) //only select edge if it does not create a cycle (ie the two nodes forming it have different root nodes) { minCost += cost; union_find(a, b); } } return minCost; } int main() { int x, y; long long weight, cost, minCost; for(int i = 0;i < MAX;++i) //initialize the array groups { root[i] = i; } p[0] = make_pair(10, make_pair(0, 1)); p[1] = make_pair(18, make_pair(1, 2)); p[2] = make_pair(13, make_pair(2, 3)); p[3] = make_pair(21, make_pair(0, 2)); p[4] = make_pair(22, make_pair(1, 3)); sort(p, p + edges); //sort the array of edges minCost = kruskal(); cout << "Minimum cost is: "<< minCost << endl; return 0; }
Output:
Minimum cost is: 4
What is Kruskal’s algorithm used for?
As we discussed, the Kruskal algorithm is used for finding the minimum spanning tree of a connected, undirected graph. Its simplicity and efficiency make it attractive for solving such problems. So, it is widely used in various fields such as computer networks, circuit design, and transportation systems, where finding a spanning tree is relatively cost-effective.
For example, in circuit design, it can be used to reduce the total length of the wires connecting components on a circuit board, or in transportation planning, Kruskal’s algorithm can be used to find the most cost-effective way to connect a set of cities by road or rail.
What is the Complexity of Kruskal's Algorithm in C++?
The time complexity of the Kruskal algorithm in C++ is O(E log E), where E is the number of edges in the input graph. These complications arise from sorting edges based on their weights, which require O(E log E) when using sorting algorithms such as quicksort, mergesort, and heapsort
In practice, the Kruskal algorithm is generally faster than other minimum spanning tree algorithms such as the Prim algorithm, especially for sparse graphs with many edges because the time complexity of the Prim algorithm is negatively O(V^2). absolutely, while Kruskal's is O( E log E). , which can be much smaller than V^2 for simple calculations
Why is Kruskal's Algorithm Greedy?
The Kruskal algorithm is a greedy algorithm because it selects the least weighted edge at each step and adds it to the current edge set as a cycle in which it constructs a minimum spanning tree by the least weighted edge which selects frequently from the input graph.
The algorithm makes a local optimal choice at each step, choosing the edge that seems to be the best at that moment, without considering the long-term effects of that choice. You can also learn about other Greedy Algorithms in C++ to solidify your DSA concepts.
Conclusion
Now you have understood Kruskal’s Algorithm and how it can be used to find a minimum spanning tree for a graph, you are ready to answer questions about it in interviews. Please try the C++ code we have given to implement it.








