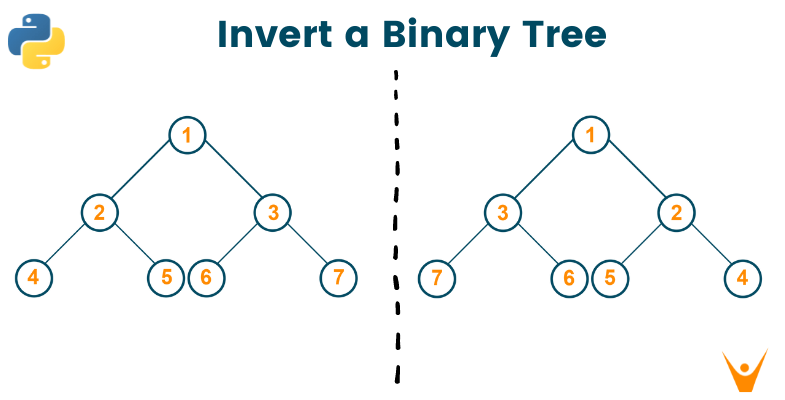
If you are looking to be part of your dream company, understanding the concepts of graphs and tree data structure should be your priority. Often, the technical interviews of companies like Microsoft, Google, and Amazon cover the questions of graphs and trees to identify the candidate’s problem-solving ability and level of understanding. Invert binary tree is one such problem that is frequently asked during technical interviews of Amazon and Microsoft. Today, we will study this problem in detail along with different methods to find its solution. But, before that, let us have a brief introduction to the binary tree.
What is a Binary Tree?
A binary tree is a data structure that arranges objects in a tree with each node containing an object and up to two additional nodes associated with the child objects. This structure is advantageous because of its ability to reorganize and easily retrieve data. Along with this, it has the benefits of both an ordered array and a linked list, making it easy to navigate and search within. A node of the binary tree has the following parts:
- Data
- Pointer to the right child
- Pointer to the left child
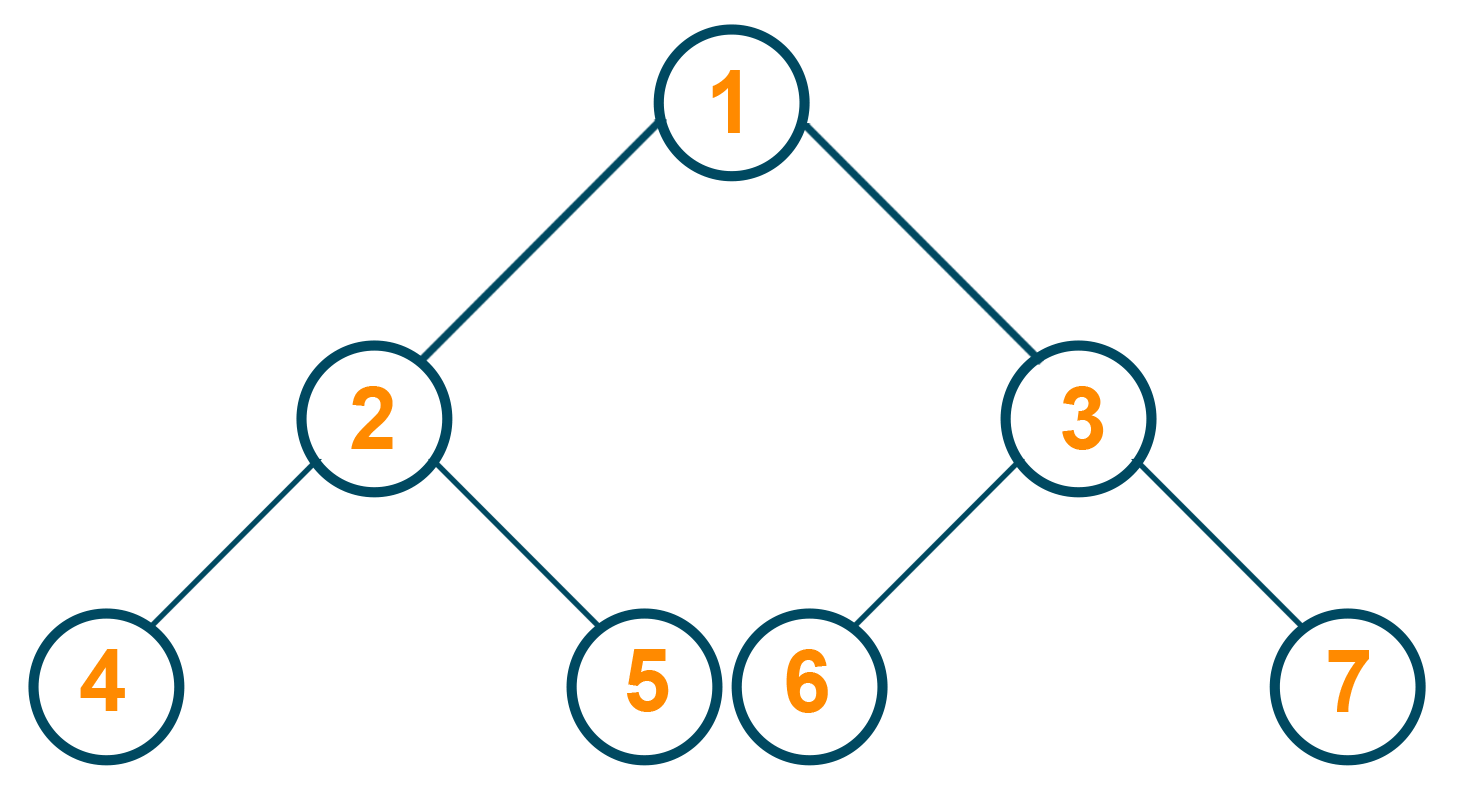
The below image shows the binary tree data structure:
What is Invert Binary Tree Problem?
"Given the root of a binary tree, invert the tree and return its root."
The problem statement suggests finding the binary tree using another one with all its left and right children nodes interchanged. You can also say that you have to find the mirror image for the given binary tree along its vertical axis.
Example
Suppose we have the below given binary tree.
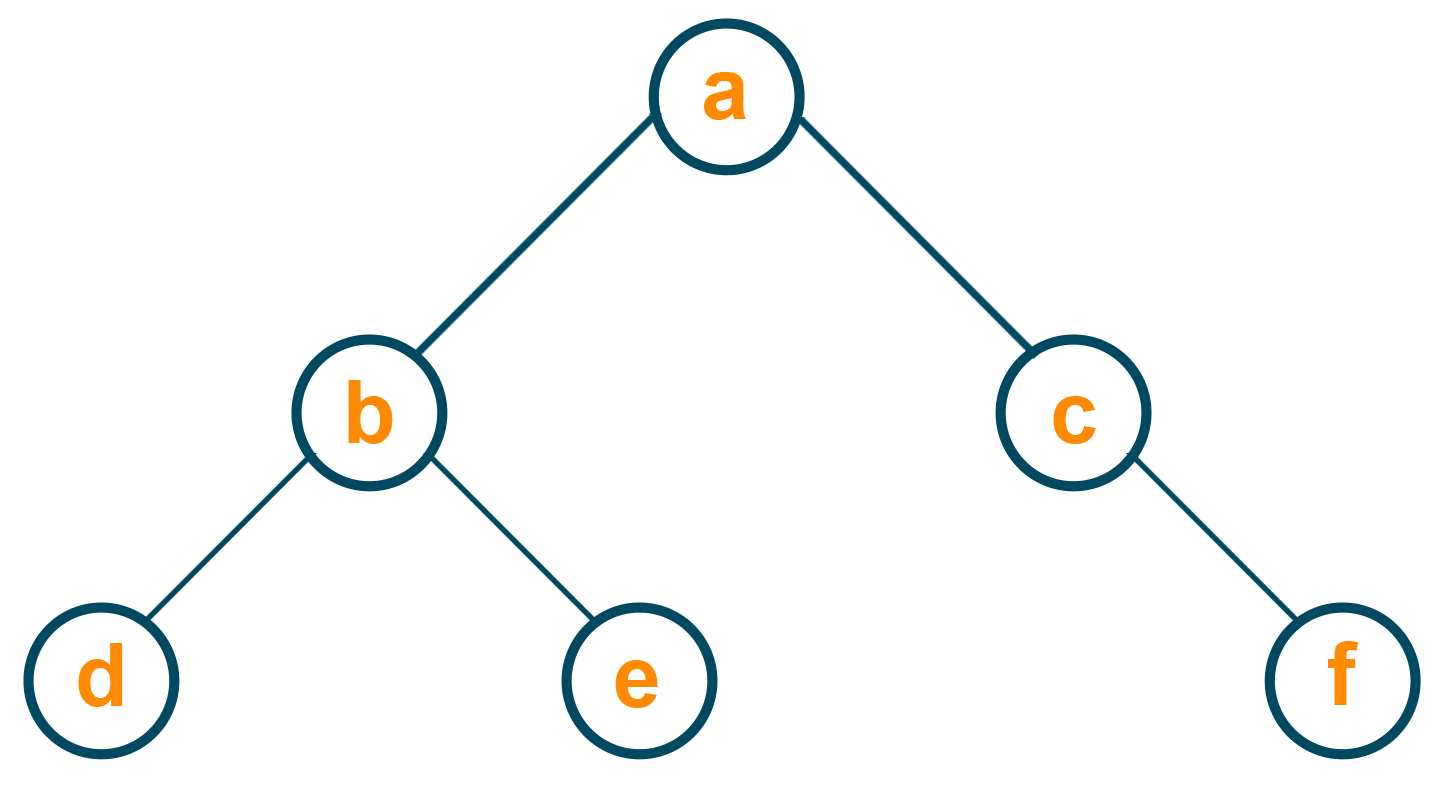
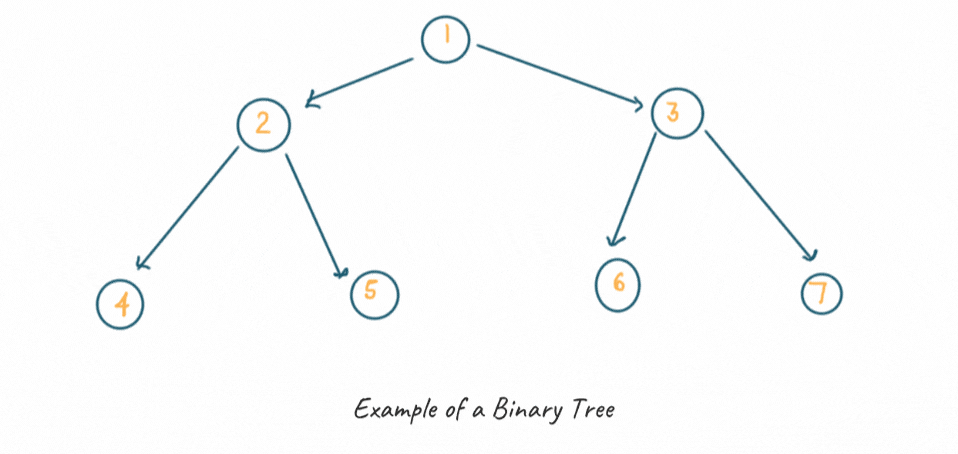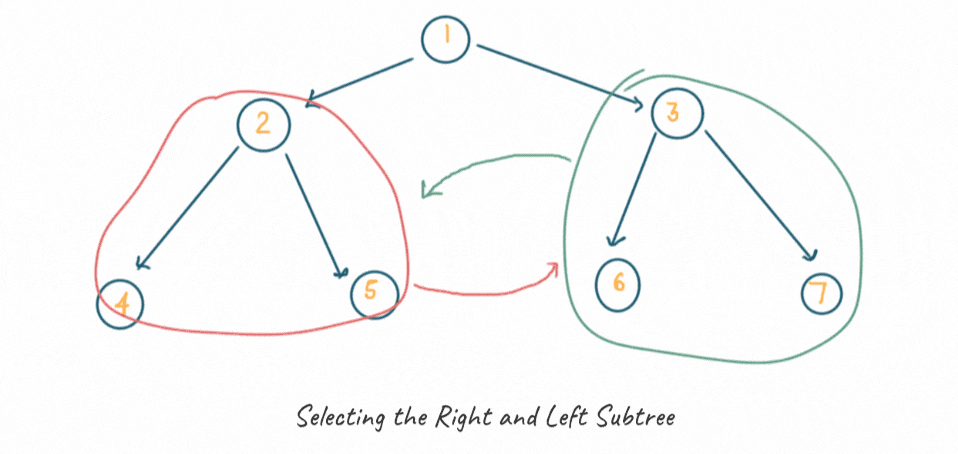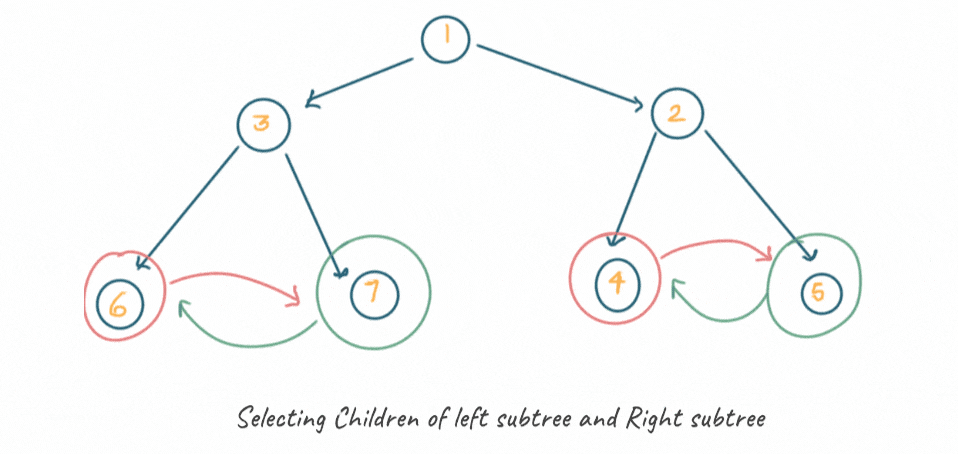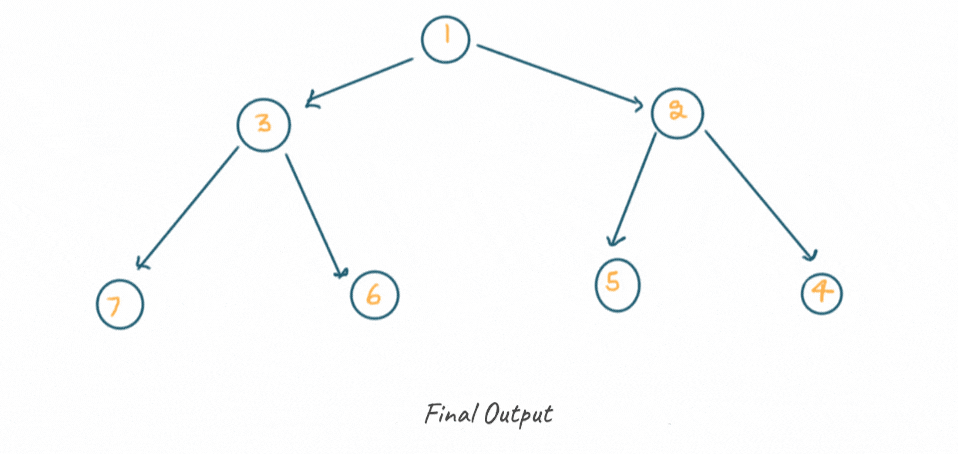
Now, we will swap the children nodes of the root node as a left and right subtree. Take a look at the below diagram for a better understanding.
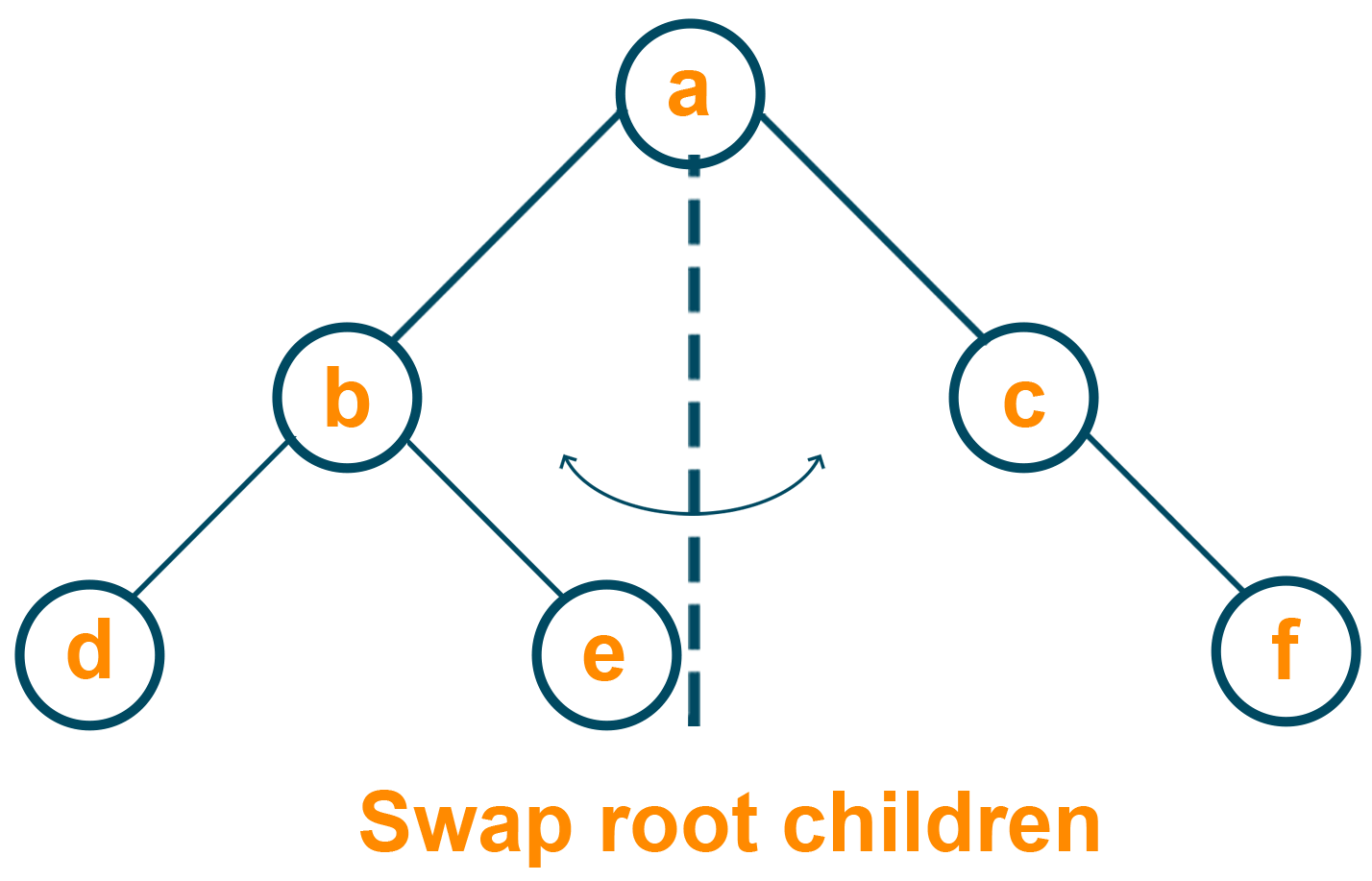
After swapping the subtree for the root node, we will swap the children nodes of the left subtree.
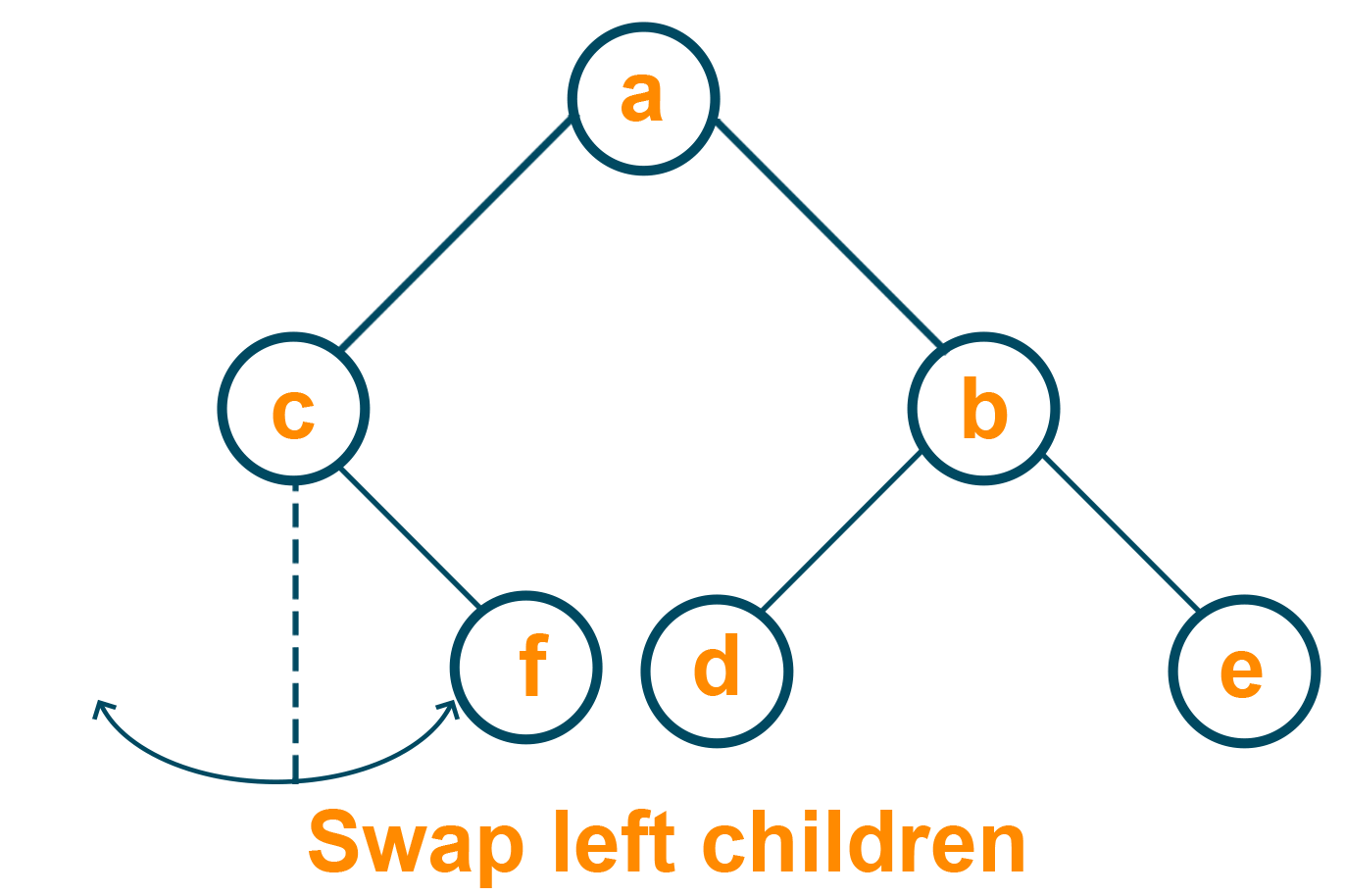
Similarly, both the children nodes of the right subtree interchange their position to find the invert of a binary tree.
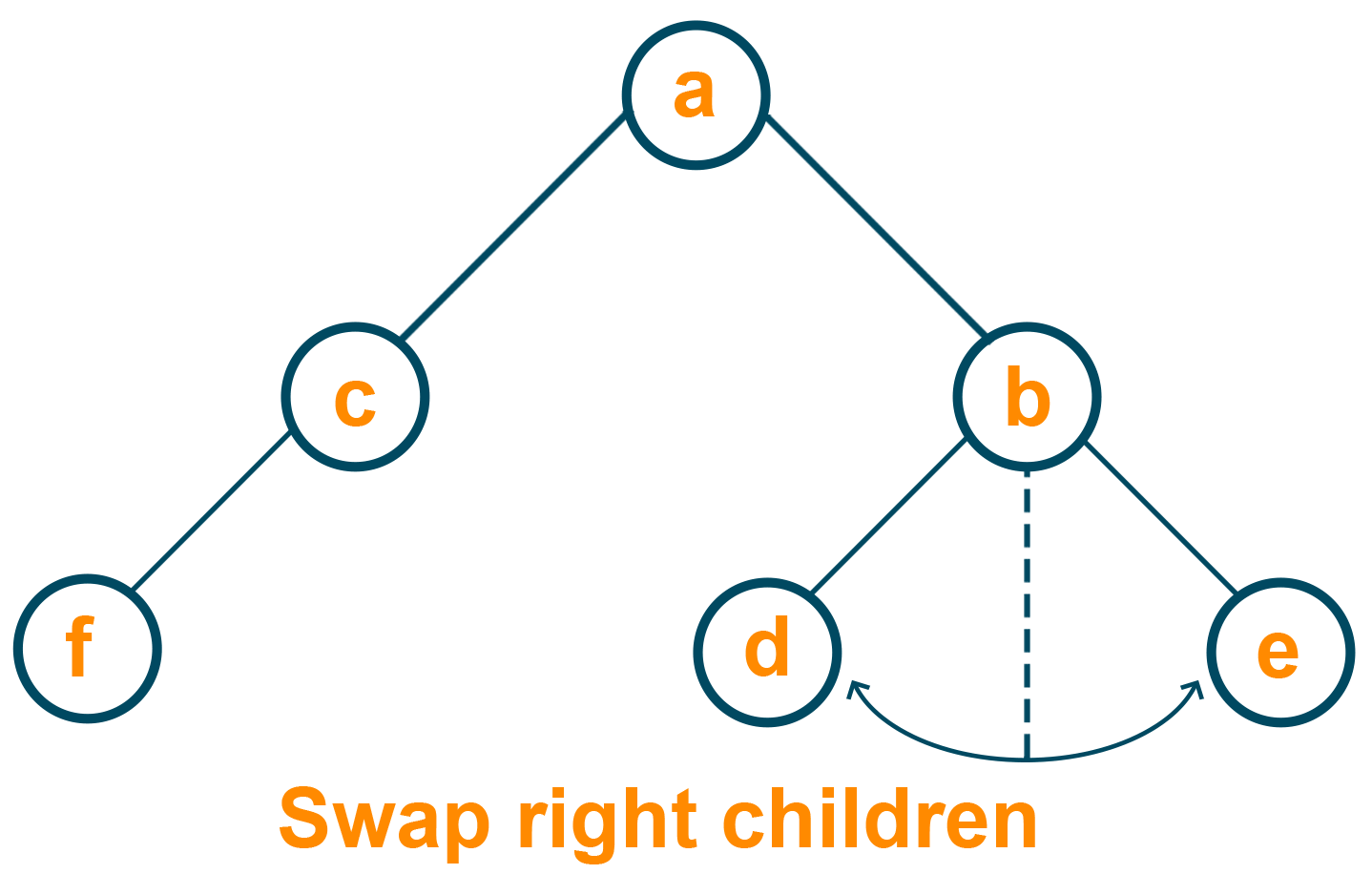
The final output of the problem will be as shown below:
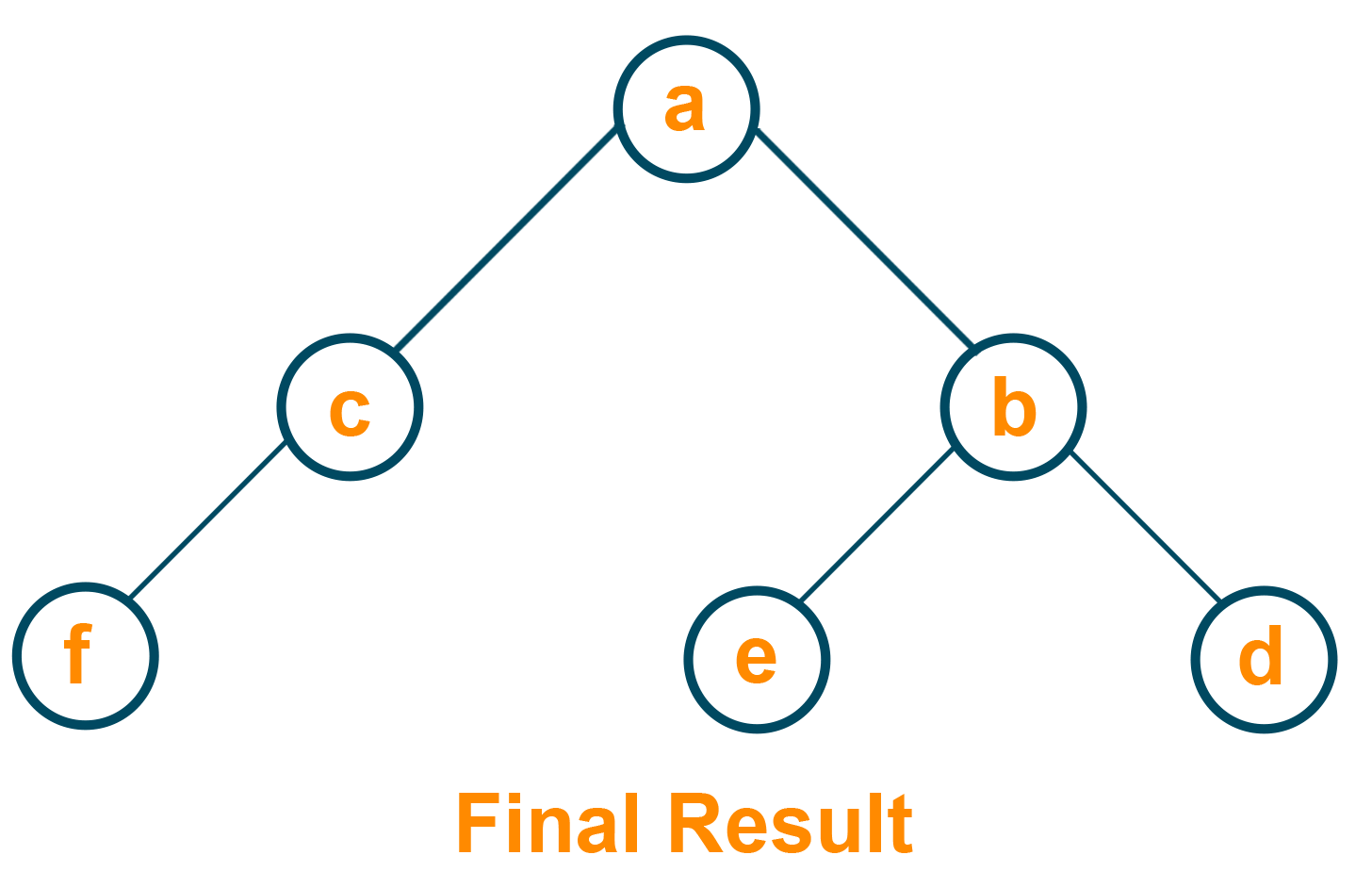
Here's the illustration of the solution for inverting a binary tree
How to Invert a Binary Tree?
You can invert a binary tree using recursive and iterative approaches. Below are the three approaches to solve this problem:
- Recursive Approach: Swapping the left and right child of every node in subtree recursively.
- Using Iterative preorder traversal: Converting recursive approach to iterative by using stack.
- Using Iterative level order traversal: Iterative approach by using a queue.
Let us discuss all these solutions in detail below:
1) Inverting a Binary Tree Using Recursive Approach
The idea is to traverse the nodes of the binary tree in a preorder fashion, and for every node you traverse, you have to swap its left and right child before inverting its left and right sub-tree recursively.
Therefore, you have to recursively solve the two smaller sub-problems of the left and right sub-tree by using the preorder traversal of the given binary tree. Remember that the output of the problem will not get affected if you wish to traverse the tree using postorder traversal.
The steps to follow while solving the problem are:
- Return NULL if the tree is empty. It will be our base case to stop the recursive calls while swapping the children nodes of the tree.
- Traverse the binary tree using preorder traversal.
- Swap left and right child for every node encountered before inverting its left and right sub-tree recursively.
Pretty simple, right? If you still find it confusing, take a look at the python code below to clear all your doubts.
Python Code (With Recursion)
class Node: def __init__(self, data): self.left = None self.right = None self.data = data def PrintTree ( self ) : if self.left : self.left.PrintTree () print ( self.data, end= ' ' ) , if self.right : self.right.PrintTree () class Solution: ''' Function to invert the tree ''' def invertTree(self, root): if root == None: return root.left, root.right = self.invertTree(root.right),self.invertTree(root.left) return root if __name__ == '__main__': ''' 10 10 / \ / \ 20 30 ========>> 30 20 / \ / \ 40 50 50 40 ''' Tree = Node(10) Tree.left = Node(20) Tree.right = Node(30) Tree.left.left = Node(40) Tree.right.right = Node(50) print('Initial Tree :',end = ' ' ) Tree.PrintTree() Solution().invertTree(root=Tree) print('\nInverted Tree :', end=' ') Tree.PrintTree()
Output
Initial Tree : 40 20 10 30 50
Inverted Tree : 50 30 10 20 40
Time Complexity
As you are traversing each node of the binary tree only once, the time complexity of the above problem will be O(n), where ‘n’ is the total number of nodes in the binary tree.
The space complexity of the above problem will be O(h). Here, the space complexity is directly proportional to the maximum depth of the recursion tree, which is equal to the height of the binary tree "h."
2) Inverting a Binary Tree Using Iterative Preorder Traversal
Stack is a linear data structure that follows a definite order to perform operations. A stack follows the LIFO(Last in First Out) principle, which means that the last element inserted in the stack will be the first element to come out. Iterative preorder traversal is used to traverse the tree using the LIFO principle using the stack data structure. Here, the recursive approach is converted to iterative by implementing stack explicitly.
The steps to follow while solving the problem using this approach is:
- Return NULL if the tree is empty.
- Create a stack ‘S’ and push the root node inside it.
- Initiate a loop until S is not empty:
- Pop element from the stack ‘S’ and swap the left child with the right child
- Push right child of popped element into S
- Push left child of popped element into S
Here note that the right child is pushed before the left child to ensure that the left subtree is processed first while inverting the binary tree.
Python Code (Iterative Preorder Traversal)
class Node: def __init__(self, data): self.left = None self.right = None self.data = data def PrintTree ( self ) : if self.left : self.left.PrintTree () print ( self.data, end= ' ' ) , if self.right : self.right.PrintTree () class Solution: ''' Function to invert the tree ''' def invertTree(self, root): if not root : return stack = [ root ] while stack : node = stack.pop() node.left , node.right = node.right , node.left if node.left : stack.append ( node.left ) if node.right : stack.append ( node.right ) return root if __name__ == '__main__': ''' 10 10 / \ / \ 20 30 ========>> 30 20 / \ / \ 40 50 50 40 ''' Tree = Node(10) Tree.left = Node(20) Tree.right = Node(30) Tree.left.left = Node(40) Tree.right.right = Node(50) print('Initial Tree :',end = ' ' ) Tree.PrintTree() Solution().invertTree(root=Tree) print('\nInverted Tree :', end=' ') Tree.PrintTree()
Output
Initial Tree : 40 20 10 30 50
Inverted Tree : 50 30 10 20 40
Time Complexity
For each node in the tree, we are performing push() and pop() operations only once, and therefore, the time complexity of the above approach is O(n), where n is the total number of nodes in the binary tree.
The space complexity for this approach is O(n) because we require a stack of size n to store all the nodes of the binary tree.
3) Inverting a Binary Tree Using Iterative Level Order Traversal
Just like the above approach, we can solve this problem using level order traversal. The only difference between both these approaches is that here we will be following the FIFO principle. Therefore instead of the stack, in this approach, we will make use of queue data structure. The queue is a linear data structure that follows the FIFO principle, which means the element inserted first from the rear end of the queue is the first element to be deleted from the front end.
Following steps should be followed in each iteration to invert a binary tree using this approach:
- Return NULL if the tree is empty
- Store the root node in the queue and iterate the loop till the queue is not empty
- During each iteration
- Delete a node from the queue
- Swap left and right child
- Insert the left and right child into the queue
Take a look at the below python code to understand how to invert a binary tree using level order traversal.
Python code (Iterative Level Order Traversal)
import collections class Node: def __init__(self, data): self.left = None self.right = None self.data = data def PrintTree ( self ) : if self.left : self.left.PrintTree () print ( self.data, end= ' ' ) , if self.right : self.right.PrintTree () class Solution: ''' Function to invert the tree ''' def invertTree(self, root): if not root : return root queue = collections.deque() queue.append(root) while len(queue) : node = queue.popleft () node.left , node.right = node.right , node.left if node.left is not None : queue.append ( node.left ) if node.right is not None : queue.append ( node.right ) return root if __name__ == '__main__': ''' 10 10 / \ / \ 20 30 ========>> 30 20 / \ / \ 40 50 50 40 ''' Tree = Node(10) Tree.left = Node(20) Tree.right = Node(30) Tree.left.left = Node(40) Tree.right.right = Node(50) print('Initial Tree :',end = ' ' ) Tree.PrintTree() Solution().invertTree(root=Tree) print('\nInverted Tree :', end=' ') Tree.PrintTree()
Output
Initial Tree : 40 20 10 30 50
Inverted Tree : 50 30 10 20 40
Time Complexity
For every node in the tree, we perform the queue operations(enqueue and dequeue) only once, and therefore, the time complexity of the above approach is O(n), where n is the total number of nodes in the tree.
Similarly, the space complexity of this solution is O(n) as it requires a queue of size n to store all the nodes of the binary tree.
Comparison of Different Approaches
|
Approach |
Time Complexity |
Space Complexity |
|
Recursive Approach |
O(n) |
O(h) |
|
Iterative Preorder Traversal |
O(n) |
O(n) |
|
Iterative Level order Traversal |
O(n) |
O(n) |
Conclusion
Competitive problems involving data structure and algorithms are the most favorite questions to be asked during any technical interviews. In this article, we learned one such problem of inverting a binary tree using three different approaches and its respective python code. If you still have any difficulty understanding the above solutions, get in touch with our expert tutors to solve your doubts immediately.