In this article, you will learn what Dynamic Programming is, the approach to solving problems using it, the principle of optimality, and how you can solve dynamic programming along with its characteristics and elements. We will also go through the 10 most important dynamic programming problems in Python. So, let's get started!
What is Dynamic Programming?
Just like the divide and conquer algorithm, Dynamic Programming solves problems by combining the solutions with sub-problems.
Divide and conquer algorithms partition the problem into independent sub-problems to solve the sub-problems recursively and then combine their solutions to solve the original problem. In contrast, dynamic programming is applicable when the sub-problem is not independent, that is when sub-problems share sub-problems.
Therefore, a dynamic programming algorithm solves every sub-problem just once and then saves its answers in a table, thereby avoiding the work of recomputing the answer every time the subproblem is encountered.
The development of a dynamic programming algorithm can be broken into a sequence of four steps:
- Characterize the structure of an optimal solution
- Recursively define the value of the optimal solution
- Compute the value of an optimal solution in a bottom-up fashion
- Construct an optimal solution from computed information
Dynamic programming algorithm is designed in a way to optimize the given problem to get output by combining the solutions of sub-problems and appearing to the “principle of optimality”.
What is the Principle of Optimality?
The dynamic programming algorithm obtains the solution using the principle of optimality. The principle of optimality states that “ in an optimal sequence of decisions or choices, each subsequence must also be optimal”. When it is not possible to apply the principle of optimality it is almost impossible to obtain the solution using the dynamic programming approach.
The principle of optimality: “If k is a node on the shortest path from i to j, then the part of the path from i to k, and the part from k to i, must also be optimal.”
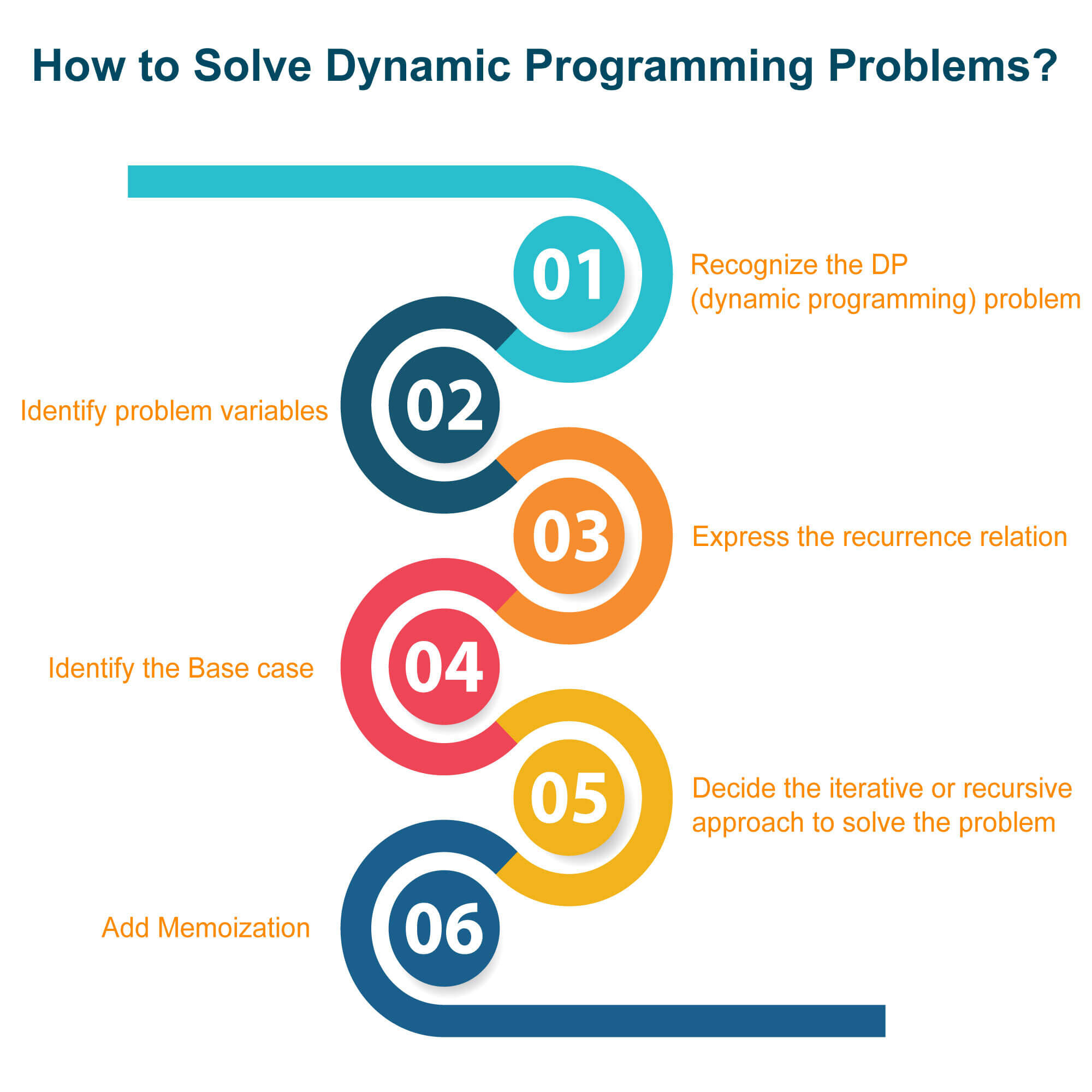
How to Solve Dynamic Programming Problems?
After knowing what dynamic programming is, it is important to learn the recipe for solving dynamic programming problems. When it comes to finding the solution to the problem using dynamic programming, below are the few steps you should consider to follow:
1) Recognize the DP problem
Identifying that the given problem statement can be solved by a dynamic programming algorithm is the most crucial step. You can solve this difficulty by asking yourself whether you can divide the given problem statements into smaller parts as a function and find its solution or not.
2) Identify problem variables
After deciding that the problem can be solved using dynamic programming, the next thing you have to do is to find the recursive structure between the subproblems of the original problem. Here, you have to consider the changing parameters of the problem. This changing parameter can be anything like the array position or the speed of the problem-solving.
Also, it is important to identify the number of subproblems of the original problem.
3) Express the recurrence relation
Many developers rush through the coding part of problem-solving and forget to define the recurrence relation. Expressing the recurrence relation clearly before coding the problem will strengthen your problem understanding and make the process efficient.
4) Identify the base case
The case is a part of the subproblem which is independent of other subproblems. In order to define the base case of your subproblem, you have to identify the point at which your problem cannot be simplified further.
5) Decide the iterative or recursive approach
Dynamic programming problems can be solved using an iterative or recursive approach. By the discussion till now, you must assume that the recursive process is better. But it is important to know that all the above points we discussed are completely independent of the problem-solving approach.
Whether you choose the iterative method or the recursive method, it is important for you to decide the recurrence relation and the base case of the problem.
6) Add memoization
Memoization is the process of storing the result of the subproblem and calling them again when a similar subproblem is to be solved. This will reduce the time complexity of the problem. If we do not use memorization, similar subproblems are repeatedly solved which can lead to exponential time complexities.
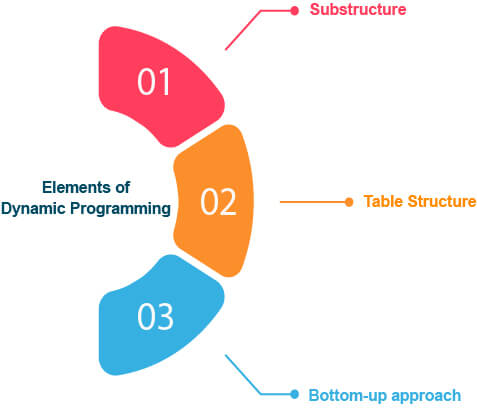
Characteristics and Elements
Before applying the dynamic programming approach to a problem statement, it is important to know that when to apply a dynamic programming algorithm. Let us understand 2 characteristics of the dynamic problem which explain the working while solving the problem statement.
1) Optimal substructure
The problem gives the optimal substructure if the optimal solution contains optimal sub-solutions in it. We can recursively define the optimal solution if the problem has an optimal substructure. Also, there is no base to define a recursive algorithm if the problem doesn’t have an optimal solution.
2) Overlapping subproblems
The problem is called overlapping subproblems if the recursive algorithm repeatedly visits the same sub-problems. If any problem has overlapping subproblems then we can improve the repetitive implementation of sub-problems by computing it only once. If the problem doesn’t have overlapping subproblems, then it is not feasible to use a dynamic programming algorithm to solve the problem.

As you have understood, dynamic programming is the algorithm that divides the problem into various sub-problems to find out the optimal solution. While solving the problem statement using the dynamic programming approach, the problem is divided into 3 elements in total to get the final result. These elements are:
- Substructure: Sub-Structuring is the process of dividing the given problem statement into smaller sub-problems. Here we manage to identify the solution of the original problem in terms of the solution of sub-problems.
- Table Structure: It is necessary to store the solution of the sub-problem into a table after solving it. This is important because as we know, dynamic programming reuse the solutions of subproblems many times so that we don’t have to repeatedly solve the same problem, again and again,
- Bottom-up approach: The process of combining the solutions of subproblems to achieve the final result using the table. The process starts with solving the smallest subproblem and later combining their solution with the subproblems of increasing size until you get the final solution of the original problem.
Top 10 Dynamic Programming Problems in Python
There are many problem statements that are solved using a dynamic programming approach to find the optimal solution. Some of the most commonly asked well-known problem statements are discussed below with a brief explanation and their corresponding Python code.
1) Knapsack (0-1) Bounded
Here, you are given the profits and weights of N items, and you have to put these items in a knapsack with the capacity ‘W’, and you have to find the number of items to be selected such that it is less than or equal to the knapsack capacity.
The knapsack problem is the perfect example of a dynamic programming algorithm and the most commonly asked question in a technical interview of product-based companies.
Problem Statement: Given a bag with capacity W and a list of items along with their weights and profit associated with them. The task is to fill the bad efficiently such that max profit is achieved.
Solution: Here, you will create a table dp[][] and consider all possible weights from 1 to W as columns and weights that you can choose as rows. The state /cell dp[i][j] in the table represents the maximum attainable profit if 'j' is the capacity of the knapsack and the first 'i' elements are included in the weight/ item array.
Thus the last cell will represent the answer state. Items can only be included if their weight is less than the capacity of the knapsack. There are two possibilities for the condition where you can fill all columns which have ‘weight>wt[i-1]’. Check out these two possibilities in detail as shown in the below problem logic:
Problem Logic:
function kProfit Case 1: if N=0 and W=0 return 0 Case 2: if wt[N-1] <= W then dp[N][W] = max(pr[N-1]+kProfit(W-wt[N-1], N-1,wt,pr,dp), kProfit(W,N-1, wt, pr, dp)) return dp[N][W] Case 3: else dp[N][W] = kProfit(W,N-1, wt, pr, dp) return dp[N][W]
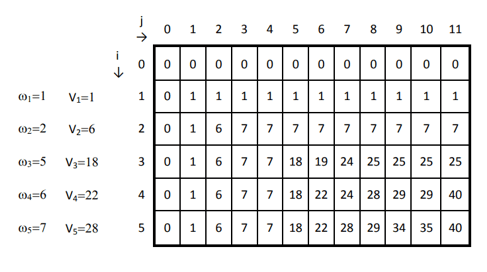
Python Code:
''' Capacity of knapsack = W weight list : wt = [] price list : pr = [] No. of items = N ''' def kProfit(W,N,wt,pr,dp): # Base Condition if N==0 or W==0: return 0 # If sub problem is previously solved tehn return it. if dp[N][W] is not None: return dp[N][W] if wt[N-1] <= W: dp[N][W] = max(pr[N-1]+kProfit(W-wt[N-1],N-1,wt,pr,dp), kProfit(W,N-1,wt,pr,dp)) return dp[N][W] else: dp[N][W] = kProfit(W,N-1,wt,pr,dp) return dp[N][W] if __name__ == '__main__': W = 11 wt = [1, 2, 5, 6, 7] pr = [1, 6, 18, 22, 28] N = len(pr) # define DP array dp = [[None] * (W + 1) for _ in range(N + 1)] # Call for kProfit to calculate max profit maxProfit = kProfit(W,N,wt,pr,dp) print('Maximum Profit is : ',maxProfit)
Output:
Maximum Profit is : 40
The running time complexity of the 0/1 Knapsack problem is O(N*W) where N is the number of items given and W is the capacity of the Knapsack.
2) 0/1 Knapsack Bounded Memoization
You are given a bag with the capacity K and a list of items with specified weight and profit that are to be inserted such that you get the maximum profit. Here we will try to solve the problem using memoization rather than tabulation.
The difference between both the 0/1 knapsack problem is that the above problem used the bottom-up approach to find the solution whereas this problem uses a top-down approach using memoization to get the output of the problem.
The reason to use memoization is that it helps to reduce the overlapping of subproblems in dynamic programming. Therefore, it reduces the problem of repeatedly solving the sub-problem and makes the process getting output faster and more effective.
Problem Statement: Given a bag with capacity W and a list of items along with their weights and profit associated with them. The task is to fill the bag efficiently such that max profit is achieved.
Solution: Firstly, you have to create a 2D array to store the results of all the subproblems which are solved. The columns of the table will display all possible weights from 1..W dividing it into W parts and rows displaying the weights you choose at any given moment.
Every time we solve a subproblem we store it in a dp array. Whenever we encounter the same subproblem we simply return the solution rather than solving it again.
Problem Logic:
function kProfit Case 1: if N=0 and W=0 return 0 Case 2: if wt[N-1] <= W then dp[N][W] = max(pr[N-1]+kProfit(W-wt[N-1], N-1,wt,pr,dp), kProfit(W,N-1, wt, pr, dp)) return dp[N][W] Case 3: else dp[N][W] = kProfit(W,N-1, wt, pr, dp) return dp[N][W]
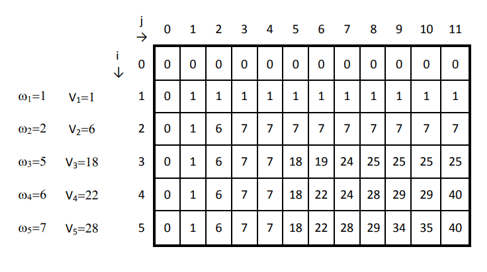
Python Code:
def kProfit(W,N,wt,pr,dp): # Base Condition if N==0 or W==0: return 0 # If sub problem is previously solved tehn return it. if dp[N][W] is not None: return dp[N][W] if wt[N-1] <= W: dp[N][W] = max(pr[N-1]+kProfit(W-wt[N-1],N-1,wt,pr,dp), kProfit(W,N-1,wt,pr,dp)) return dp[N][W] else: dp[N][W] = kProfit(W,N-1,wt,pr,dp) return dp[N][W] if __name__ == '__main__': W = 11 wt = [1, 2, 5, 6, 7] pr = [1, 6, 18, 22, 28] N = len(pr) # define DP array dp = [[None] * (W + 1) for _ in range(N + 1)] # Call for kProfit to calculate max profit maxProfit = kProfit(W,N,wt,pr,dp) print('Maximum Profit is : ',maxProfit)
Output:
Maximum Profit is : 40
The running time complexity of the problem is O(N*W) where N is the number of items present and W is the capacity of the knapsack.
3) Subset Sum Problem
The subset sum problem is the most frequently asked question in technical interviews with Microsoft and Infosys. The subset sum problem is the problem of finding the subset of the given set of numbers where the sum of the elements of the subset found is equal to the target number.
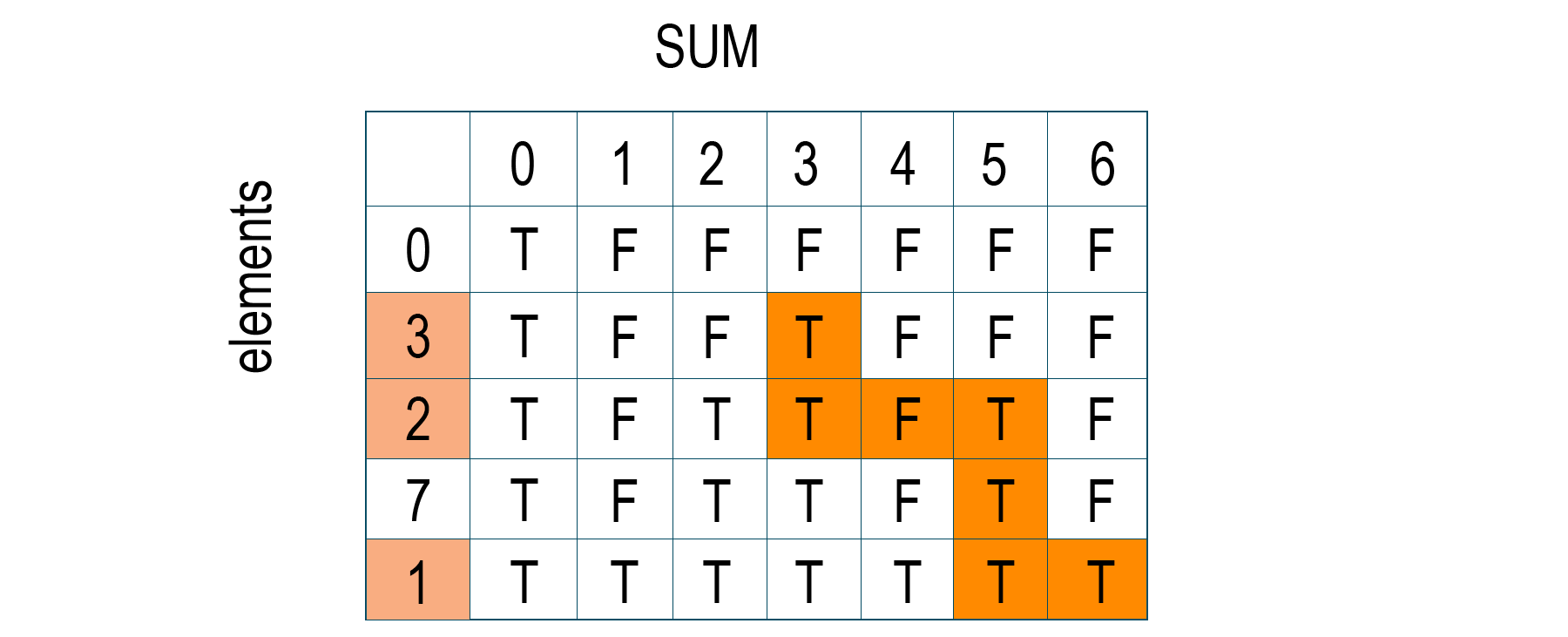
Problem statement: You are given an array and target. You have to find if there exists any subset that will sum equal to the target.
Solution: Here you will create a 2D array of size (arra.size()+1)*(target+1) of boolean type. Later, you will set the value of each state dp[i][j] true if a subset of elements arr[0...i] exists with the sum value to be 'j' where j is the target number.
Problem Logic:
if (arr[i-1] < j) // if can be included
dp[i][j] <-- dp[i-1][j] or dp[i-1][j-A[i-1]]
else // cannot be included
dp[i][j] <-- dp[i-1][j]
Python code:
def subSum(arr,target): n = len(arr) dp = [[None]*(target+1) for _ in range(n+1)] # Initialise DP array !! # If no. of elements in arr are 0 then Target sum is not possible # Target sum = 0 is always possible i.e, by keeping the array subset as null/phi. for i in range(target+1): dp[0][i] = False for j in range(n+1): dp[j][0] = True # An element can be chosen only if sum is less han arr[i] else it cannot be included for i in range(1,n+1): for j in range(target+1): if arr[i-1] <= j: dp[i][j] = dp[i-1][j-arr[i-1]] or dp[i-1][j] else: dp[i][j] = dp[i-1][j] return dp[n][target] if __name__ == '__main__': arr = [0, 3, 2, 7, 1] target = 6 exists = subSum(arr,target) print('Subset with Target sum exists : ', str(exists))
Output:
Subset with Target sum exists: True
The time complexity of the above problem is O(target sum*n), where n is the size of the array.
4) Equal Subset Problem
The equal subset problem uses dynamic programming to find the partition of the given set such that the sum of elements of both subsets is the same. The equal subset problem is also known as the partition problem and is a very good example of a dynamic programming algorithm.
Problem Statement: Given an array arr. You have to divide the array into halves such that the sum of the two subsets is equal.
Solution: You have to create a 2D array of size (sum/2+1)*(target+1). Here, you can store the output for every subset and every sum and then retrieve the output while partitioning the original array. The first dimension in the 2D array will represent the different possibilities of subset and the second dimension will represent the different possibilities of sum using the combinations of subsets.
Problem Logic:
if (arr[i-1] > j) dp[i][j] = dp[i-1][j] else dp[i][j] = dp[i-1][j] or dp[i-1][j-arr[i-1]]

Python code:
def subSum(arr,target): n = len(arr) dp = [[None]*(target+1) for _ in range(n+1)] # Initialise DP array !! # If no. of elements in arr are 0 then Target sum is not possible # Target sum = 0 is always possible i.e, by keeping the array subset as null/phi. for i in range(target+1): dp[0][i] = False for j in range(n+1): dp[j][0] = True # An element can be chosen only if sum is less han arr[i] else it cannot be included for i in range(1,n+1): for j in range(target+1): if arr[i-1] <= j: dp[i][j] = dp[i-1][j-arr[i-1]] or dp[i-1][j] else: dp[i][j] = dp[i-1][j] # Return last cell as it contains answer return dp[n][target] def isPossible(arr): # If arr has sum P and two subsets have same sum S respectively then S+S =P. Therefore we need to find # subset of sum P//2 and other subset will have same sum. P = sum(arr) S = P // 2 # ReturnTrue if subset exists else False return(subSum(arr,S)) if __name__ == '__main__': arr = [3, 1, 1, 2, 2, 1] # An array can be divided into two equal halves only if sum of arr is even else it is not possible if sum(arr) % 2: print('Equal Subset cannot be formed !!') else: boolean = isPossible(arr) if boolean: print('Equal Sum Subsets are possible !') else: print('Equal Sum Subsets are not possible !')
Output:
Equal Sum Subsets are possible
The running time complexity of the above code is O(target*n) where the target is the ‘target sum’ and n is the length of the array
5) Longest Common Subsequence
The longest common subsequence problem is the most commonly asked question in Google Interview. Here the problem involves finding the longest subsequence that is present in the two given strings in the same order. Therefore, the output should be the longest sequence that can be obtained by deleting some items from the first and second original strings.
Problem Statement: You are given two strings s1 and s2, of length l1 and l2, respectively. You have to find the length of the longest common subsequence of s1 and s2.
Solution: This problem differs from the Longest Common Substring problem as in substrings, sequences are not necessary to occupy consecutive positions within the original string. Solving this problem using a dynamic programming approach will reduce the number of function calls to find the common sequence.
Using dynamic programming, you have to generate a table dp(1..m, 1…n) where m is the length of string s1 and n is the length of string s2.
At any instance, if the characters of two strings match then you increment the value from the previous subproblem else you look for an answer by taking the maximum from two subproblems created by decrement either string by one i.e., looking for characters other than unmatched characters.
Problem Logic to generate the table dp[i][j] as shown below where i and j represent the row and column of the table.
Problem Logic:
Make dp[i][0] and dp[0][j] if xi = yi then dp[i, j] <- dp[i-1, j-1]+1 else if dp[i-1, j] >= dp[i, j-1] then dp[i, j] <- dp[i, j] <- dp[i-1, j] else dp[i, j] <- dp[i, j-1]

Python code:
def LCS(s1,s2,l1,l2): dp = [[None]*(l2+1) for _ in range(l1+1)] # Initialise dp # If length of any substring is 0 then length of LCS will be zero # So dp[0][i] and dp[j][0] will be zero for i in range(l1+1): dp[i][0] = 0 for j in range(l2+1): dp[0][j] = 0 # if s1[i] == s2[j] then increase by 1 else search in i-1 and j or i and j-1 for i in range(1,l1+1): for j in range(1,l2+1): if s1[i-1] == s2[j-1]: dp[i][j] = 1 + dp[i-1][j-1] else: dp[i][j] = max(dp[i][j-1],dp[i-1][j]) # dp[l1][l2] contains the length of LCS of s1 and s2 return dp[l1][l2] if __name__ == '__main__': s1 = 'abbacdcba' s2 = 'bcdbbcaa' maxlen = LCS(s1,s2,len(s1),len(s2)) print("Length of LCS = ",maxlen)
Output:
Length of LCS =5
The time complexity of the above problem is O(m*n), where m is the length of s1 and n is the length of s2.
6) Longest Common Substring
The longest common substring problem is the problem of finding the longest string which is also the substring of two different strings. Sounds confusing? Let's look forward and understand it in detail.
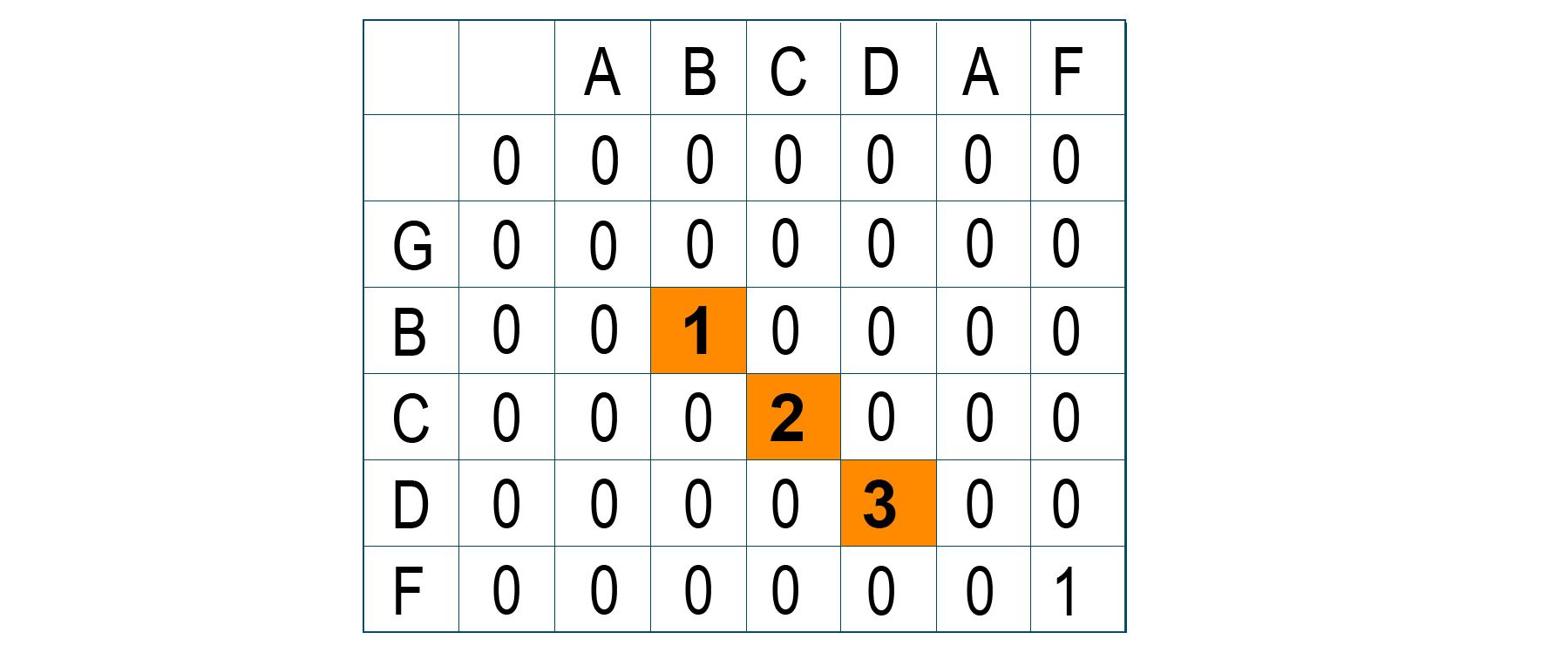
Problem Statement: You are given the strings s1 and s2. You have to find the length of the longest common substring of s1 and s2.
Solution: Here you can start checking all substrings from the first string s1 with the character of the second string s2 and keep a record of the maximum. You can solve this problem using dynamic programming by following the bottom-up manner.
Create a matrix of size len(s1)*len(s2) and store the value of the solutions of the substrings to use later to solve similar subproblems. The problem is similar to the Longest Common Subsequence problem with the only difference that if the characters do not match then the answer at that instance becomes 0.
Problem Logic:
Base Case: If any string is null then LCS will be 0 else, compare the ith character of string A with jth character of string B. Case 1: If both characters are same, LCS[i][j] = 1 + LCS[i-1][j-1] (adding 1 to the result and remove the last character from both strings) Case 2: If both characters are not same LCS[i][j] = 0 At last, traverse the matrix and find the maximum character in it. The output will be the length of the Longest Common Substring.
Python code:
def SubString(s1,s2,l1,l2): dp = [[None]*(l2+1) for _ in range(l1+1)] # Initialise dp # If length of any substring is 0 then length of LCS will be zero # So dp[0][i] and dp[j][0] will be zero for i in range(l1+1): dp[i][0] = 0 for j in range(l2+1): dp[0][j] = 0 # If s1[i] == s2[j] then increase by 1 else dp[i][j] will be 0 as substring will break for i in range(1,l1+1): for j in range(1,l2+1): if s1[i-1] == s2[j-1]: dp[i][j] = 1 + dp[i-1][j-1] else: dp[i][j] = 0 maximum = -9999 for i in dp: maximum = max(maximum,max(i)) return maximum if __name__ == '__main__': s1 = 'aabcdaf' s2 = 'gbcdf' maxlen = SubString(s1,s2,len(s1),len(s2)) print("Length of Longest Common Substring = ",maxlen)
Output:
Length of Longest Common Substring =3
The running time complexity of the above problem is O(m*n), where m is the length of s1 and n is the length of s2.
7) Longest Palindromic Sequence
The largest palindromic sequence problem finds the characters of the sequence from the given string, which are palindromic in nature. It is the sequence of characters that are read and spelled in the same way from forward and backward. Unlike the longest palindromic substring problem, the sequences may or may not occupy consecutive positions within the original string.
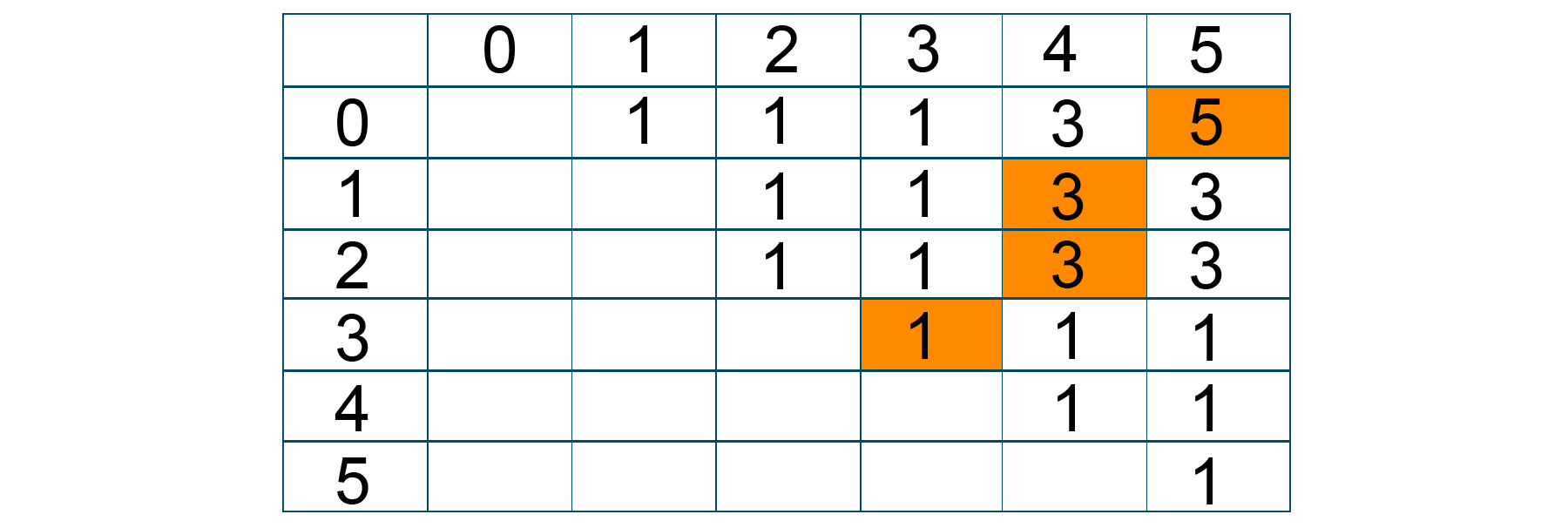
Problem Statement: Given a string ‘S’. The task is to find the length of the largest palindromic sequence.
Solution: Here, the problem shows the characteristics of the dynamic programming approach i.e., optimal substructure and overlapping subproblems. The problem shows a direct resemblance with the Longest Common Substring problem. But How?? You are given only one string!
Even though you are given only a string, by close observation we find that the Longest Palindromic Subsequence is actually the Longest Common Substring between the string and its reverse.
Problem Logic:
Case 1: If the first and last character is equal then add the first and last character into the palindromic sequence and recur the remaining substring again. Case 2: If the first and last characters are different then return the maximum among the two and remove the same character from the substring.
Python Code:
def LCS(s1,s2): l1 = len(s1) l2 = len(s2) dp = [[None]*(l2+1) for _ in range(l1+1)] # Initialise dp # If length of any substring is 0 then length of LCS will be zero # So dp[0][i] and dp[j][0] will be zero for i in range(l1+1): dp[i][0] = 0 for j in range(l2+1): dp[0][j] = 0 # if s1[i] == s2[j] then increase by 1 else search in i-1 and j or i and j-1 for i in range(1,l1+1): for j in range(1,l2+1): if s1[i-1] == s2[j-1]: dp[i][j] = 1 + dp[i-1][j-1] else: dp[i][j] = max(dp[i][j-1],dp[i-1][j]) # dp[l1][l2] contains the length of LCS of s1 and s2 return dp[l1][l2] def LPS(s): # Length of the Largest palindromic subsequence is equal to Longest Common Subsequence of string s and reversed(s) srev = s[::-1] return LCS(s,srev) if __name__ == '__main__': s = 'agbdba' length = LPS(s) print(f'Length of the largest Palindromic Subsequence is {length}')
Output:
Length of the largest Palindromic Subsequence is 5
The time complexity of the above problem is O(2^n), where n is the length of the given string.
8) Longest Repeating Subsequence
The longest Repeating subsequence serves as the best example of a dynamic programming problem. The problem gets the output of the longest sequence of characters from the given string which is repeated irrespective of the order of the string
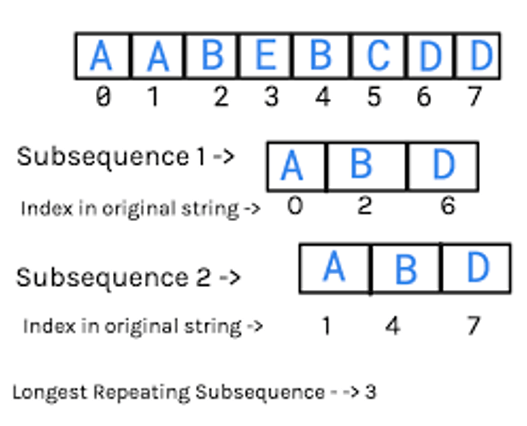
Problem Statement: Given a string s. Find the length of the largest repeating subsequence in it.
Solution: The longest repeating subsequence problem is the modified version of the longest common subsequence problem. Therefore, in this problem, you have to find the longest common subsequence of the string where the given string will itself be s1 and s2 for the LCS problem. T
herefore, you have to ignore the case where the indexes of both string are the same while comparing the characters as the repeated character hold a different index in the given string
This problem contains the characteristic of dynamic programming i.e. overlapping and optimal structure, you can divide the problem into several subproblems just like the LCS problem, and store the result of each problem in the table.
Problem Logic:
Step 1: Take the given input string Step 2: Calculate the longest common subsequence where s1[i]=s1[j] and i is not equal to j Step 3: As a result, return the length of the output sequence
Python Code:
def LarRep(s,s1): n = len(s) # dp array definition dp = [[0]*(n+1) for _ in range(n+1)] # initialisation of dp array for i in range(1,n+1): for j in range(1,n+1): # increment count if index not same else chose max from previous sub problems if s[i - 1] == s1[j - 1] and i != j: dp[i][j] = 1 + dp[i - 1][j - 1] else: dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) return dp[n][n] if __name__ == '__main__': s = 'aabebcdd' length = LarRep(s,s) print(f"Length of Largest Repeating Subsequence : {str(length)}")
Output:
Length of Largest Repeating Subsequence : 3
The running time complexity to find the longest repeating subsequence is O(n^2) where n is the length of the input string.
9) Coin Change Minimum Problem
This is one of the famous dynamic programming problems which is mostly asked in technical interviews for getting into top companies. Here, the minimum coin change problem is to make a change of the given value of cents where you have an infinite supply of each of C = {c1, c2,….cm} valued coins.
Problem Statement: Given an array of available denominations of coin and one target price. Find the minimum number of coins required to pay the same.
Solution: Here, you can start the solution with sum = N cents. In each iteration, find the minimum coins required by dividing the original problem into subproblems.
Consider a coin from { 1, c2,…cm} and reduce the sum repeatedly depending upon the coin of the denomination you choose. You have to repeat the same process until N becomes 0, and at this point, you found your solution.
Problem Logic:
Base Case: If N==0, then 0 coins are considered Case 1: If N>0 then, minCoinsRequired(N, coins[0,1,2..m-1]) = min(1+ minCoinsRequired(N-coins[i], coins[0…m-1])) where i is from 0 to m-1 and coin[i] <= N
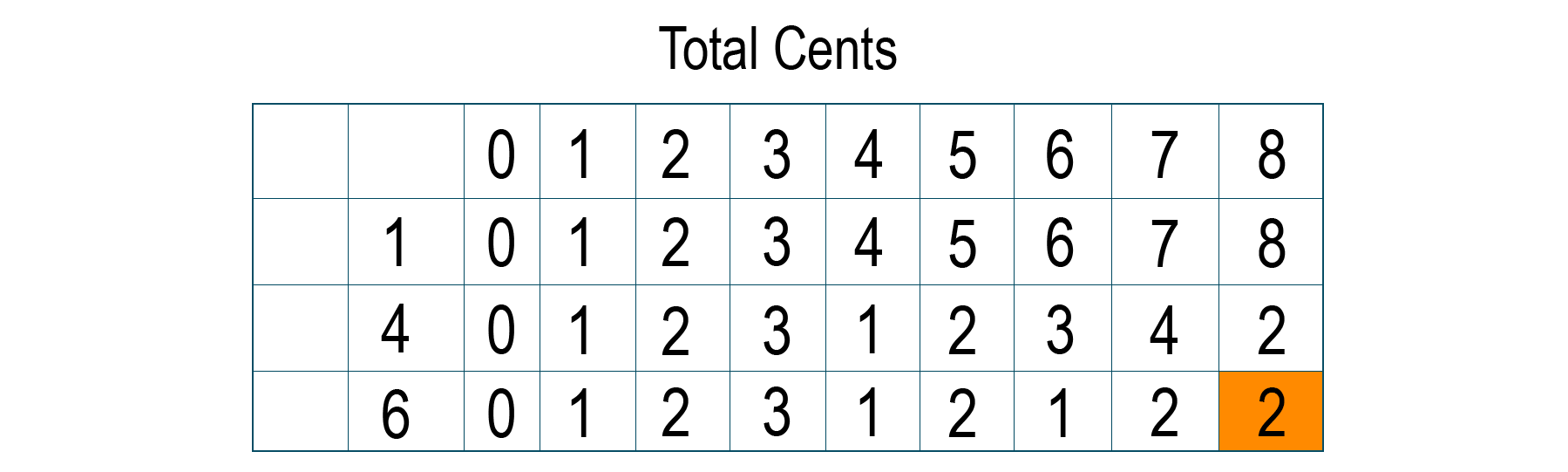
Python Code:
import sys def minCoins(coins,price): n = len(coins) # define dp array dp = [[None]*(price+1) for _ in range(n+1)] # Initialise DP array # If price = 0 then min coins needed = 0 considering null set. So dp[i][0] = 0. # If no. of coins = 0 then we would need infinite coins to get to price. So dp[0][j] = inf -1 ("-1 to avoid overflow) for j in range(price+1): dp[0][j] = sys.maxsize -1 for i in range(n+1): dp[i][0] = 0 # A coin can be selected only if its value is less than required price for i in range(1,n+1): for j in range(1,price+1): if coins[i - 1] <= j: dp[i][j] = min(dp[i - 1][j], 1 + dp[i][j-coins[i-1]]); else: dp[i][j] = dp[i - 1][j]; return dp[n][price] if __name__ == '__main__': coins = [1, 4, 6] price = 8 ch = minCoins(coins,price) print(f'Minimum number of coins required : {ch}')
Output:
Minimum number of coins required: 2
The running time complexity of the coin change minimum problem is O(m*n), where m is the number of coins and n is the change required.
10) Coin Change Ways
Coin change ways is a similar problem to the coin change problem that you learned earlier. Here, you are given value N and you have to make a change of these N cents with an infinite supply of each c=(c1, c2, ..cn) valued coin. Unlike the coin change problem, in this problem, you have to find out the distinct number of ways to make change for N cents.
Remember here the order of the coin doesn’t matter.
Problem Statement: Given an array of available denominations of coin and one target price. In how many ways can you pay the price provided you can use any coin any number of times?
Solution: Here you can see that the problem has characteristics of a dynamic programming approach i.e. optimal structure and overlapping subproblem nature and therefore, you can solve the above problem easily using dynamic programming. To solve the problem, you have to create a 2D array to store the subproblem solution.
The size of the table ‘dp’ will be (n+1)*(price+1). The rows of the table will display the denomination of coins and the column will display the total amount i.e. the sum of the cents. We will repeatedly store the value of each subproblem in the DP table and the value in the last row and the last column of the table is the final answer.
Compare the denomination value and the sum value repeatedly and run the loop to find the result of each subproblem and solve it in the table. Check out the below problem logic for a better understanding of the solution to the problem.
Problem Logic:
if c[i-1] > j then dp[i][j] = dp[i][j-c[i-1]] + dp[i-1][j] else dp[i][j] = dp[i-1][j] return dp[n][price]

Python Code:
def maxWays(coins,price): n = len(coins) # Define dp array dp = [[None]*(price+1) for _ in range(n+1)] # Initialise dp Array. # If No of coins available is 0 then there is no way to pay. So dp[0][j] = 0 # If price = 0 then it is possible to pay considering null set. So dp[i][0] = 1 for i in range(n+1): dp[i][0] = 1 for j in range(price+1): dp[0][j] = 0 # A coin can be used only if its value is less than the price so coin[i] <= price # Now if a coin is chosen once then it can be included any number of times for i in range(1,n+1): for j in range(1,price+1): # check if coin[i] < price if coins[i-1] <= j: dp[i][j] = dp[i][j-coins[i-1]] + dp[i-1][j] else: dp[i][j] = dp[i-1][j] return dp[n][price] if __name__ == '__main__': coins = [1,2,3] price = 5 ch = maxWays(coins,price) print('Max Ways to Pay : ', ch)
Output:
Max Ways to Pay : 5
The time complexity of the above problem is O(n*N) where n is the total number of denominations and N is the total change required.
House Robber is another big problem that was asked about in coding interviews.
Dynamic Programming vs Greedy Programming
Here is a complete table of differences between Dynamic and Greedy programming:
|
Dynamic Programming |
Greedy Programming |
|
Make a decision at each step considering the current problem and solution to the previously solved problem to calculate the optimal solution. |
Make whatever choice is best at a certain moment in the hope that it will lead to optimal solutions. |
|
Guarantee of getting the optimal solution. |
No such guarantee of getting an optimal solution. |
|
Slower in comparison to greedy programming. |
Faster in comparison to dynamic programming. |
|
Based on the recursive nature to use the previously calculated results. |
Make use of locally optimal choices at each step. |
|
Example: 0/1 Knapsack Problem. |
Example: Fibonacci Series. |
Learn more about greedy programming.
Advantages & Disadvantages
The biggest advantages of Dynamic Programming is that you can obtain the both local and total optimal solution, it reduces the lines of the code, & it is applicable to both linear and non-linear problem.
However, DP makes unnecessary memory utilization. As you make use of the table while solving the problem, it needs a lot of memory space for storage purposes
Applications of Dynamic Programming
Following are some major practical applications of Dynamic Programming:
- It is used in the 0/1 Knapsack Problem which is most commonly asked in technical interviews.
- It is used in a time-sharing scheduling algorithm.
- It is used widely while solving a mathematical optimization problem.
- It is used in flight and robotics control.
- It is used in routing algorithms.
- It is mostly used in computer networks and graph problems.
What are Sub Programs in Dynamic Programming?
By dividing a problem through smaller subproblems as well as storing the solutions for these smaller subproblems, dynamic programming provides a strategy for problem-solving. In dynamic programming, we resolve an issue by first resolving its sub-issues, then combining their resolutions to resolve the issue at hand.
A subproblem is a scaled-down version of the main problem. We divide the main problem into smaller, similarly structured, but more manageable subproblems. Although each subproblem is easier to tackle, they all share the same structure as the main issue. Recursively addressing the subproblems, we find solutions and record them in a table.
The fundamental problem is then resolved using the subproblem solutions. Take the issue of locating the nth Fibonacci number as an illustration. This issue can be resolved via dynamic programming by dissecting it into smaller issues.
The sum of the (n-1)th and (n-2)th Fibonacci numbers is the nth Fibonacci number. As a result, we may get the (n-1)st and (n-2)st Fibonacci numbers and then add them to solve the issue recursively. To avoid having to compute the answers to the subproblems again, we can store them in a table and utilize them to calculate the answer to the main problem.
What is Memorisation in Dynamic Programming?
Dynamic programming uses the memory approach to save the outcomes of subproblems in a table so they can be reused later. Memory is a type of caching that is employed to quicken the process of problem-solving.
When a subproblem is encountered again, the outcome of the previous subproblem is stored in a table and can be retrieved using memory. As there is no need to solve the same subproblem more than once, this method can greatly reduce the algorithm's time complexity.
Take the Fibonacci sequence, for instance. The formula F(n) = F(n-1) + F(n-2) defines the series, where F(0) = 0 and F(1) = 1. With the aid of dynamic programming and memoization, we can identify the nth phrase in the sequence. The solution to each subproblem can be kept in a table and used to determine the sequence's subsequent term.
By using this method, the algorithm's time complexity is reduced from exponential to linear. A table or an array can be used to implement memory by storing the outcomes of subproblems. As the algorithm resolves each subproblem, the values in the table can be changed. The table can be initialized with default values.
It is possible to use memorization for issues with overlapping subproblems, which means that the algorithm will run into the same subproblem more than once.
def fibonacci(n, memo): if memo[n] != -1: return memo[n] if n == 0 or n == 1: result = n else: result = fibonacci(n-1, memo) + fibonacci(n-2, memo) memo[n] = result return result n = 10 memo = [-1]*(n+1) print(fibonacci(n, memo))
When should it be used to solve a problem?
The powerful method of dynamic programming can be applied to a variety of issues. However, there are several requirements that must be satisfied before choosing to utilize dynamic programming to solve an issue, therefore it isn't always the best option.
- Overlapping Subproblems: The existence of overlapping subproblems in the original problem is one of the essential conditions for dynamic programming. In other words, the issue can be divided into more manageable subproblems that are used repeatedly in the resolution.
- Optimal substructure: The problem's optimal substructure is another prerequisite for dynamic programming. In other words, the problem's optimal solution can be created from the answers to its individual subproblems.
- Memory work can enhance performance: By saving the outcomes of pricey function calls in memory, dynamic programming methods can run better. Memorization can drastically lower the number of function calls necessary if the same subproblem appears numerous times in the solution.
- Complexity in polynomial time: Algorithms for dynamic programming should have polynomial time complexity. That is, the amount of time needed to solve the issue should be inversely correlated with some polynomial function of the size of the input.
Conclusion
Dynamic programming in Python is most important to optimize the solutions to the problem in comparison to the recursive approach. It helps to reduce the repeated function calls and hence proves to be faster and more effective than the recursive and divide-and-conquer approaches.
The idea of simply storing the results of subproblems and making use of them in computing the rest of the problem make dynamic programming algorithm a different and important topic in the domain of data structure and algorithm. Therefore, it is surely asked in every technical interview and highly recommended to learn and understand.








