Getting started with competitive programming might seem difficult but once you start solving problems consistently it will help you to crack top companies interviews. One such important problem to practice is the Combination Sum. This problem comes under the backtracking technique, one of the important topics to be covered to master competitive programming.
Combination Sum Problem Statement
Given a list of integers and a target integer, we have to return a list of all unique combinations of candidates where the chosen numbers sum to the target. We can return the combinations in any order. The same number may be chosen from the list an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
Sample Input: nums = [2,3,5], target = 8
Sample Output: [[2,2,2,2], [2,3,3], [3,5]]
This problem statement can be solved in a number of ways using various approaches. We are going to solve this using the backtracking technique since we have to find all the possible combinations as the solution. So let's get an insight into backtracking before moving on to the approach to solving the problem.
What is Backtracking?
Backtracking is an algorithmic technique that traverses and finds every possible combination for a computational problem. If a solution is not suitable, that particular solution is eliminated and then we backtrack to try other possible combinations. Backtracking is implemented using recursion.
The ultimate goal of using the backtracking approach is to use the brute force approach i.e., getting all possible solutions available for a problem under given conditions.
Here is the algorithm step-by-step:
- First, sort the input list in ascending order to get the output in increasing order.
- Then, remove all the reoccurring values from the list, since duplicate values in the input list can produce duplicates in the output list. But we want output without any duplicates.
- We try to find the possible solutions with the recursive backtracking approach. We have two base conditions to check. One condition is to check whether the target value becomes negative at any point in time. If the target value becomes negative then it denotes that the particular solution is not suitable and we can ignore searching through it.
- And another one is checking whether the target value became zero. If the target value becomes zero then it denotes that we have attained the required target through searching. So we have to add that temporary list values to the output list.
- Else add the present index in that list to the current list and recursively call the function with target = target - cand[i] and index as the current i value, then remove that element.
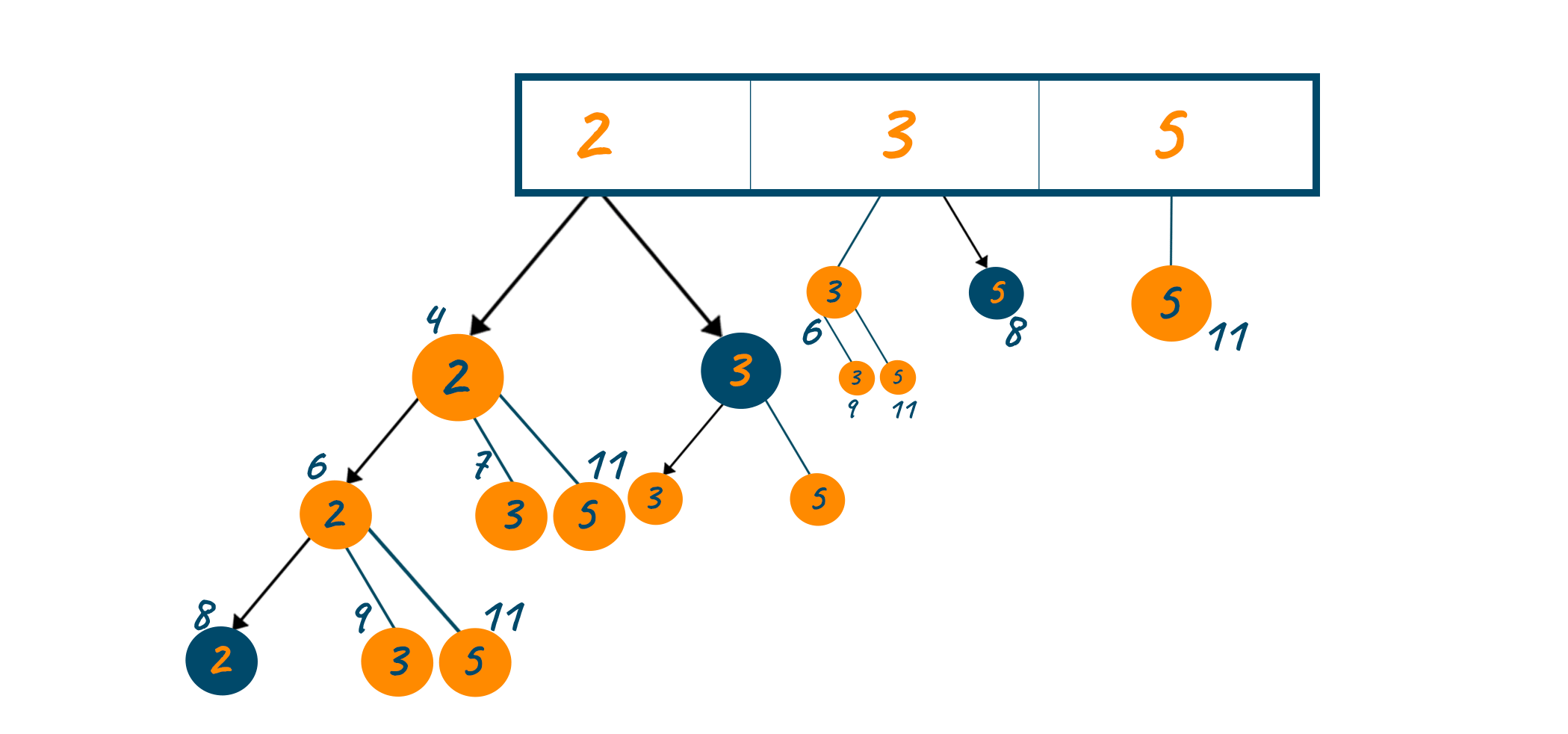
Let's understand with an example. Consider the input list [2, 3, 5] for our example and the target sum is 8. We have to find all the possible combinations with this input. First sort all the elements in the list to make the further process easy.
Then for the first element 2, check whether the target value is negative or zero by subtracting the target value from 2. If both are not true then again call the function recursively until either of the condition is true. By repeating the recursive call we can reach a point where 2+2+2+2 equals 8. Thus we got one combination sum that is equal to the required target.
In a similar way, we get two more combinations 2+3+3 and 3+5 which also sums up the target. The process is more clearly explained with the following visual representation.
Java Code for Combination Sum
Here is the Java program to find the combination sum:
import java.util.*; public class Main { public static List combinationSum(int[] candidates, int target) { List result = new ArrayList(); Arrays.sort(candidates); backtrack(candidates, 0, target, new ArrayList(), result); return result; } public static void backtrack(int[] cand, int start, int target, List list, List result) { if (target < 0) return; if (target == 0) result.add(new ArrayList(list)); for (int i = start; i < cand.length; i++) { list.add(cand[i]); backtrack(cand, i, target - cand[i], list, result); list.remove(list.size() - 1); } } public static void main (String args[]){ int[] nums = {2, 3, 5}; int target = 8; List output = combinationSum(nums, target); System.out.print(output); } }
Output:
[[2,2,2,2], [2,3,3], [3,5]]
C++ Code for Combination Sum
Here is the C++ Implementation:
#include <bits/stdc++.h> using namespace std; void findNumbers(vector<int>& ar, int sum,vector<vector<int> >& res, vector<int>& r,int i) { if (sum == 0) { res.push_back(r); return; } while (i < ar.size() && sum - ar[i] >= 0) { r.push_back(ar[i]); findNumbers(ar, sum - ar[i], res, r, i); i++; r.pop_back(); } } vector<vector<int> > combinationSum(vector<int>& ar, int sum) { sort(ar.begin(), ar.end()); ar.erase(unique(ar.begin(), ar.end()), ar.end()); vector<int> r; vector<vector<int> > res; findNumbers(ar, sum, res, r, 0); return res; } int main() { vector<int> ar; ar.push_back(2); ar.push_back(3); ar.push_back(5); int n = ar.size(); int sum = 8; vector<vector<int> > res = combinationSum(ar, sum); if (res.size() == 0) { cout << "Empty"; return 0; } for (int i = 0; i < res.size(); i++) { if (res[i].size() > 0) { cout << " ( "; for (int j = 0; j < res[i].size(); j++) cout << res[i][j] << " "; cout << ")\n"; } } return 0; }
Output:
[[2,2,2,2], [2,3,3], [3,5]]
The time complexity to solve the Combination sum using backtracking is (2^t )* k. Where k is the average length of the input and t is the length of the recursive call. This time is quite large but due to the recursive call, we can only able to implement it with this efficiency.
Considering the space complexity it will be k * n, where n is the number of combinations in the output and k is the average length of the input list. Hence if the combinations are more for the given input then space complexity will also increase.
Python Code for Combination Sum
This Python code executes the aforementioned algorithm:
def combinationSum(nums, target): nums.sort() result = [] def dfs(currIndex, remaining, currList): if remaining == 0: result.append(currList[:]) return for i in range(currIndex, len(nums)): if nums[i] > remaining: break if i > currIndex and nums[i] == nums[i-1]: continue currList.append(nums[i]) dfs(i+1, remaining-nums[i], currList) currList.pop() dfs(0, target, []) return result
To prevent duplicates, the array is sorted first in the code above. The dfs function is then defined, which has three input parameters: the current index, the balance of the sum, and the current combination.
We loop through every number in the array within the dfs function, determine whether the sum of the remaining numbers is higher than or identical to the current number, and then run the dfs method recursively with the updated parameters. After identifying every potential combination for the current number, we take it out of the mix and go on to the next number.
The result list comes back with all the potential combinations that add up to the goal value once the dfs function is called with the initial arguments.
Conclusion
As we have discussed an approach to solve the combination sum problem there are a lot more problems you can explore to gain good knowledge about backtracking and competitive programming.
If you are just getting started with competitive programming it will take some time to understand the concepts but being consistent and practicing more and more will definitely help to achieve good results. Our tutors are available 24/7 if you need help with data structures and algorithms.








