If you are a computer science student or even related to this field, you must have heard of backtracking and its significance. In most technical interviews, recruiters tend to ask mind-boggling questions regarding concepts like recursion, backtracking, and different algorithms. So, in this tech blog, we shall be discussing the very popular Backtracking algorithm. Not only this but we'll also learn and understand 10 of the most commonly asked backtracking problems with their C++ code. So, let's get started!
What is Backtracking?
Backtracking is an algorithmic concept that is used to solve computational problems in programming. It uses the brute force approach(naive approach) to find all the possible solutions to a given problem and later, choose the most optimal one. It compiles all the possible answers and later removes those that do not satisfy the provided constraints. So, when do we use this algorithm? When we have multiple solutions and want to find the most optimal one.
As the name suggests it means going back and then coming forward. Various problems can be easily solved using this algorithm. We're going to see many several problems like those, but first, let's see the easiest algorithm for backtracking.
Backtracking Algorithm
Below we've given a snippet of the easiest explanation of the backtracking algorithm, with which you can understand it in no time! Take a look!
Backtrack(x)
if x is not a solution
return false
if is a new solution
add to the list of solution
backtrack(expand x)
Here, we've defined a function called 'Backtrack' which takes an argument that could be a possible solution. If that element is not a solution, we discard it and move further. However, if it turns out to be a new solution which means that it is not already mentioned in the list of solutions, then we add it to the list. And later, we check which out of all the solutions is the most feasible.
Well, now you've seen the rough algorithm but, when do we need to use it? Let's understand that too!
When to use a Backtracking Algorithm?
The biggest confusion of all time has always been which algorithm/concept to be used for which type of questions. At FavTutor, we always help you to improve your programming skills, so see the below reasons to know when to use backtracking:
- The given information is not sufficient so, we need to try out all the possible solutions to find the most optimal one.
- each decision leads to a new cluster of choices, so we need to check out every one of them, thus using backtracking.
Terminologies used
To understand any algorithm and its working, you must understand the terminologies related to that, so read on:
- Live Node: The node on which you are currently and which can be generated further.
- E Node: Those nodes which are further generated and could become a successful node.
- Dead Node: The node which cannot be generated any further and is essentially a dead end.
- Success Node: That node that provides a feasible solution.
Understanding its Working with an Example
Now, that you've seen the basic algorithm, we're sure you must be curious to understand its works as well. We understand that it is difficult to understand and grasp an all-new concept quickly. So, we've provided an easy example of this concept to make you understand its basic functioning.
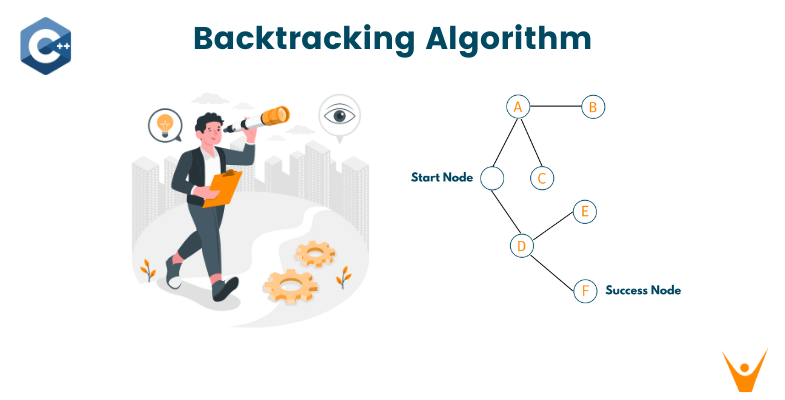
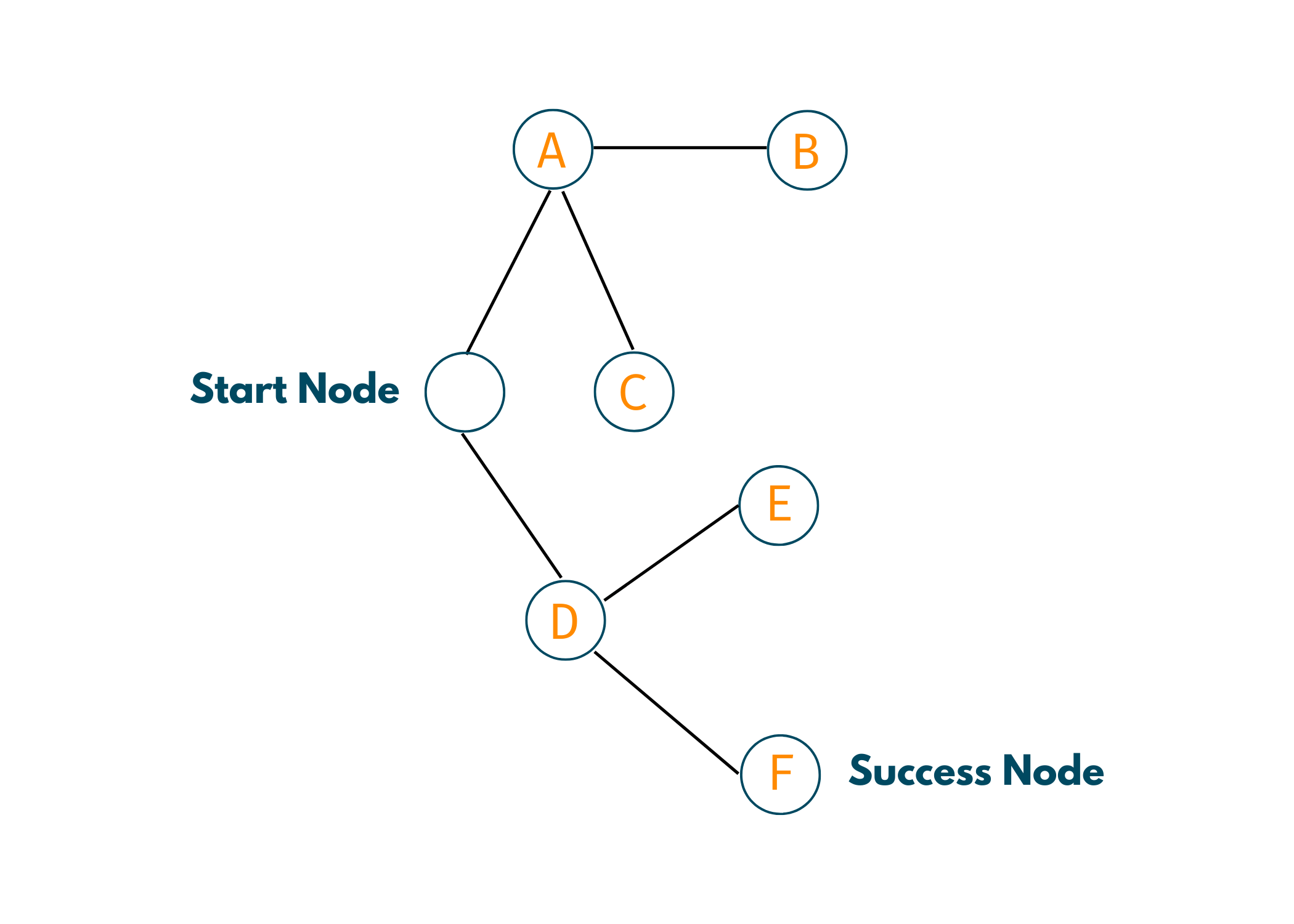
Take a look at the below network of nodes and notice that there is one starting node and one success node, but many dead ends. Let's see how we can devise the path from starting node to success one using the concept of Backtracking concept.
1. Start -> A -> B
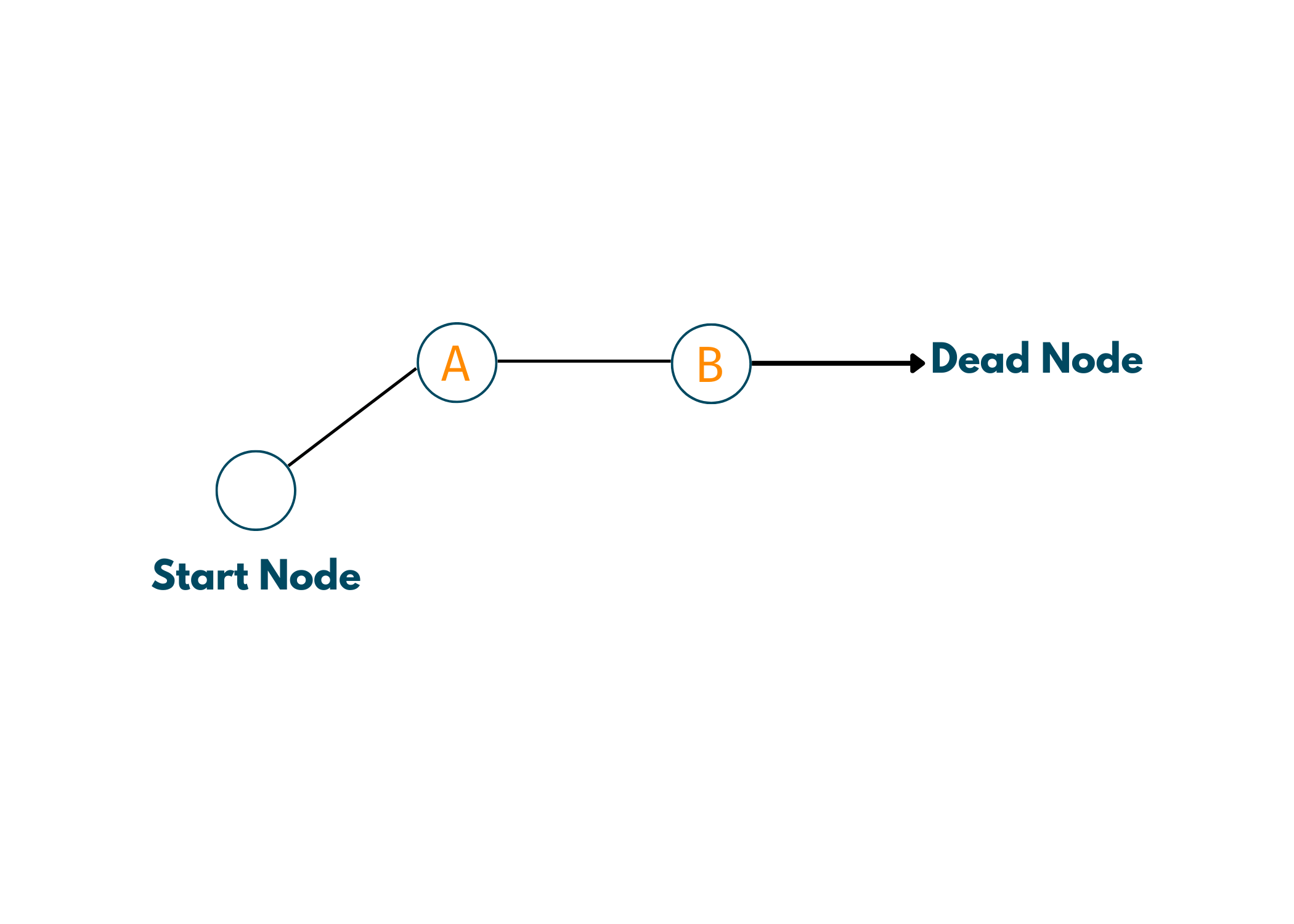
So, we start with the starting node and turn towards A. Now, only one way is there to move towards B. But, when we go further from B, we see that there is no potential success node and that it is a dead end. So, we come back to A, in other words, we backtrack to A.
2. A -> C
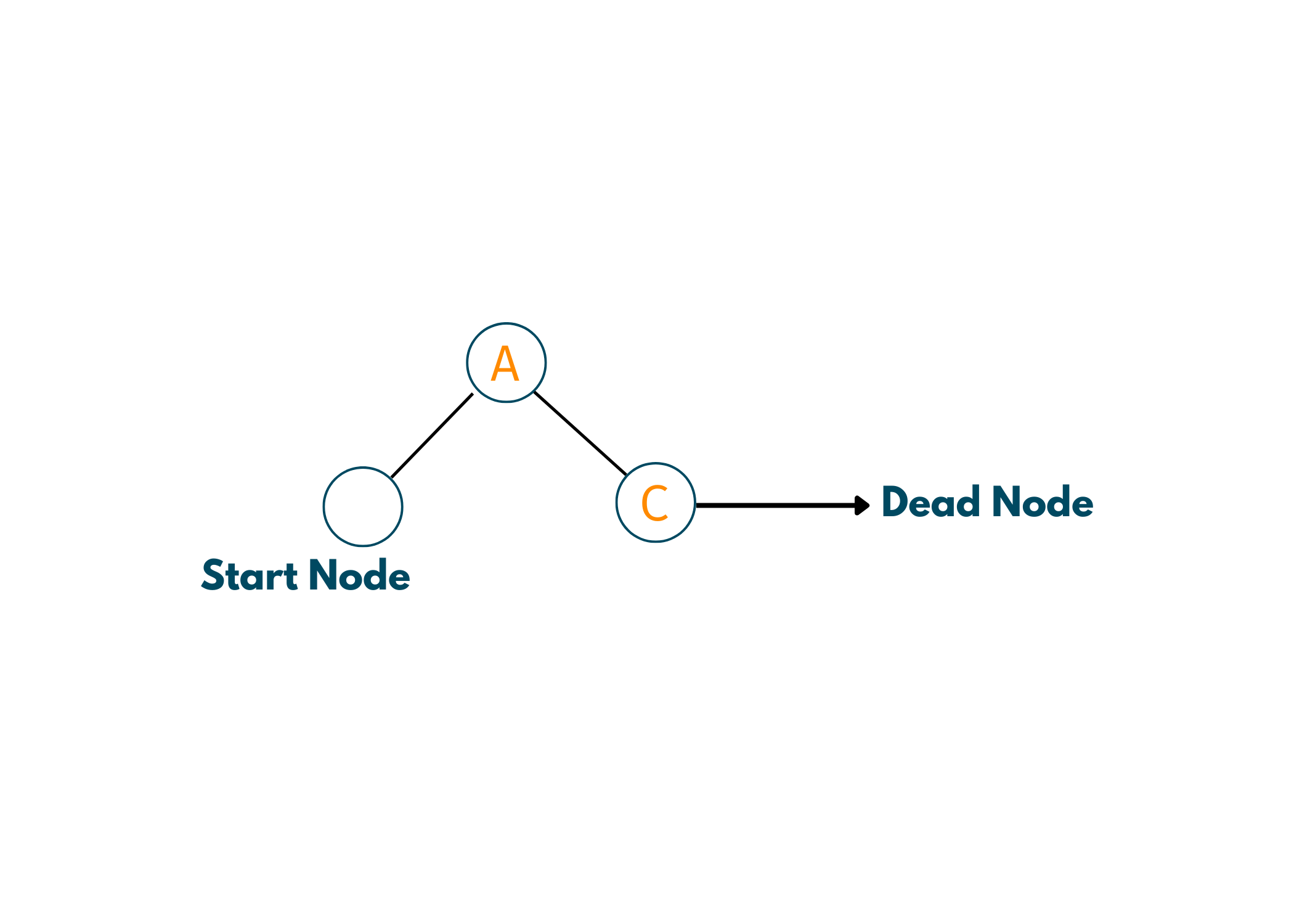
Since we have backtracked to A, we see at other nodes we can go. So, we go to C. Now, from C also we do not have any other nodes hence, a dead end again. So, we backtrack to the starting node.
3. Start -> D -> E
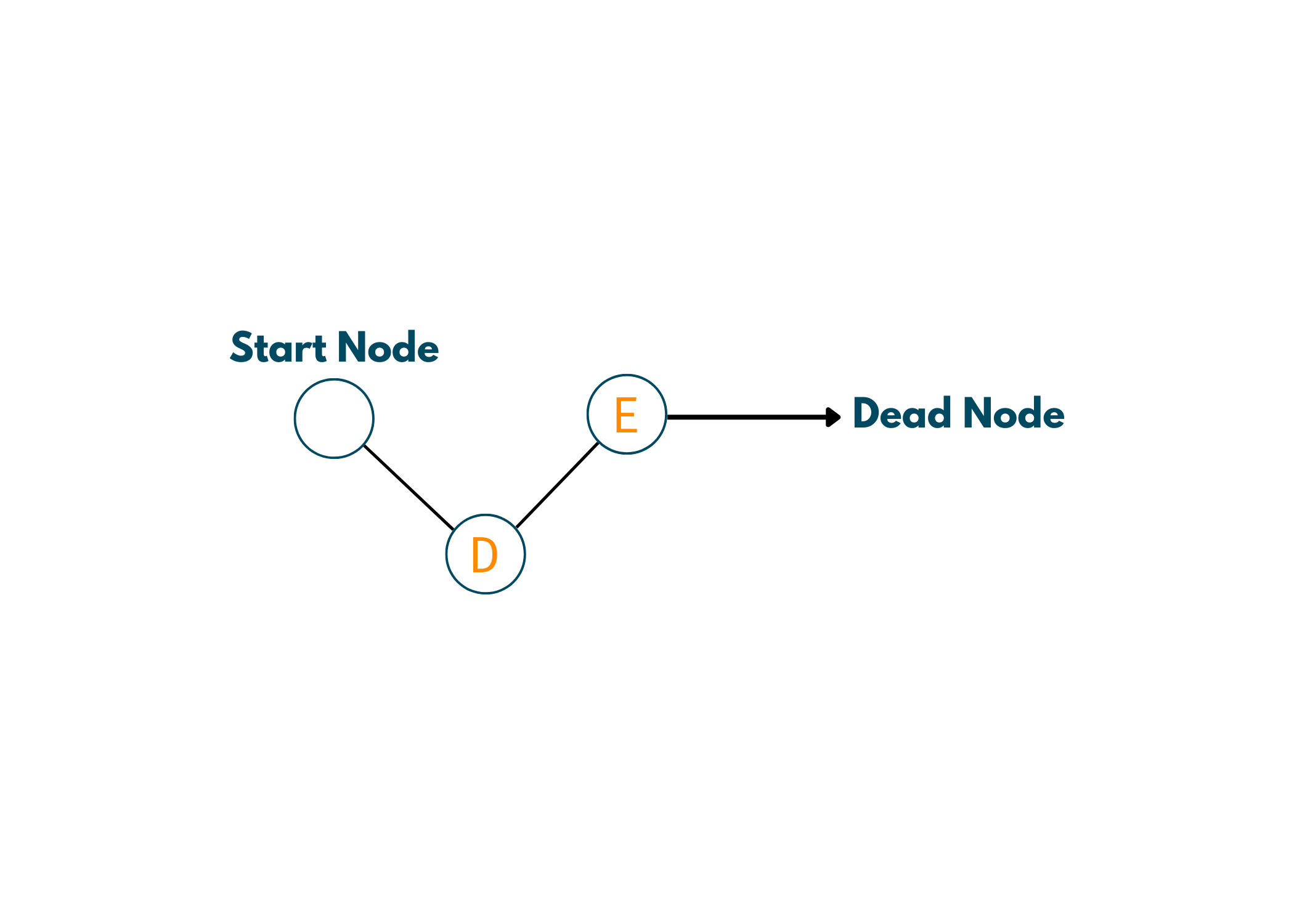
Now we are at the starting node. So, we go towards D and then E. Now, even here there is no other route, so we are again at a dead end. Hence, we backtrack to D.
4. D -> F
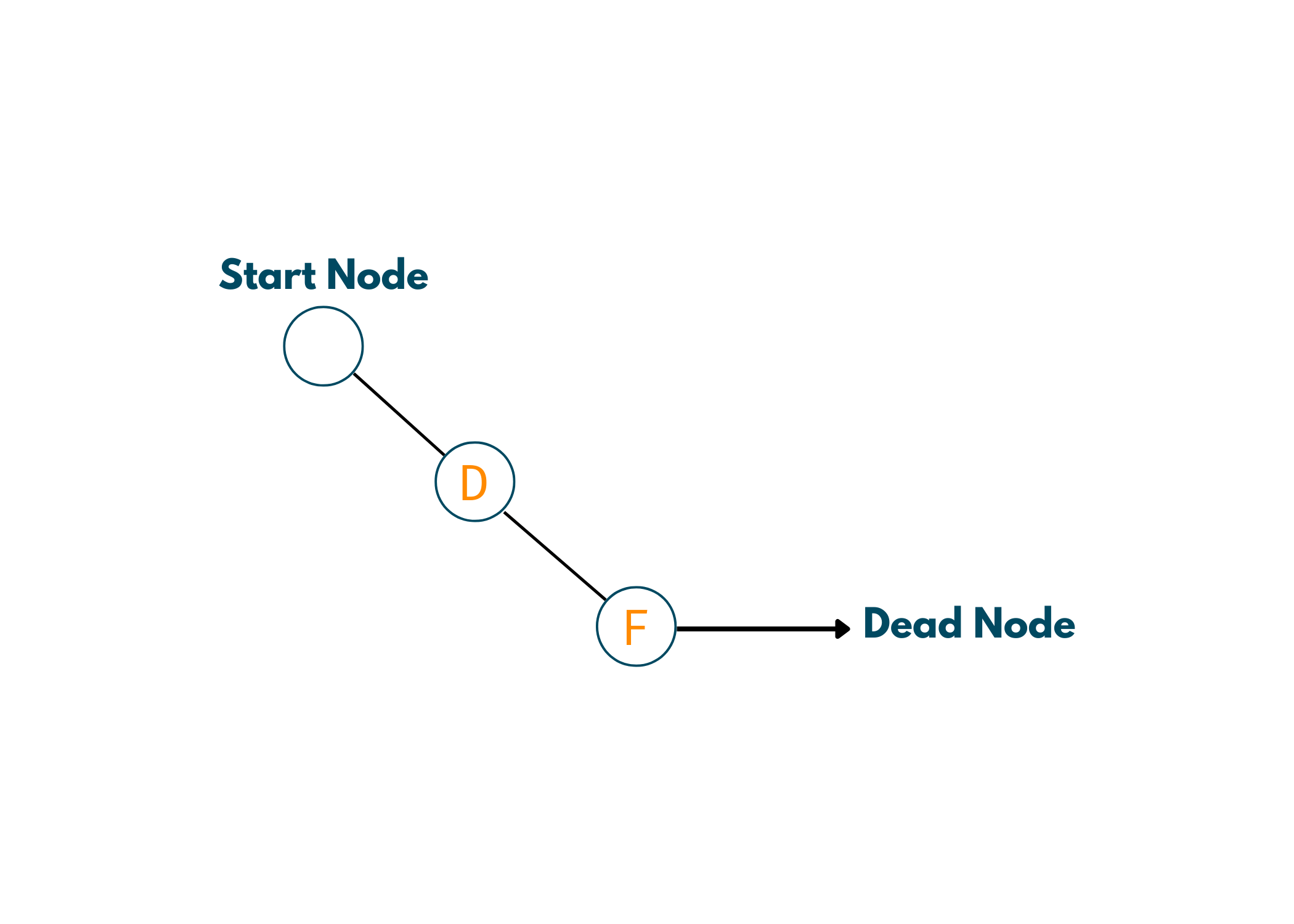
After backtracking to D, we see that we can go to F. And now, we see that we've reached the Success Node.
So, the feasible path from starting node to the success node is Start -> D -> F. Look at the below illustration for a clear understanding.
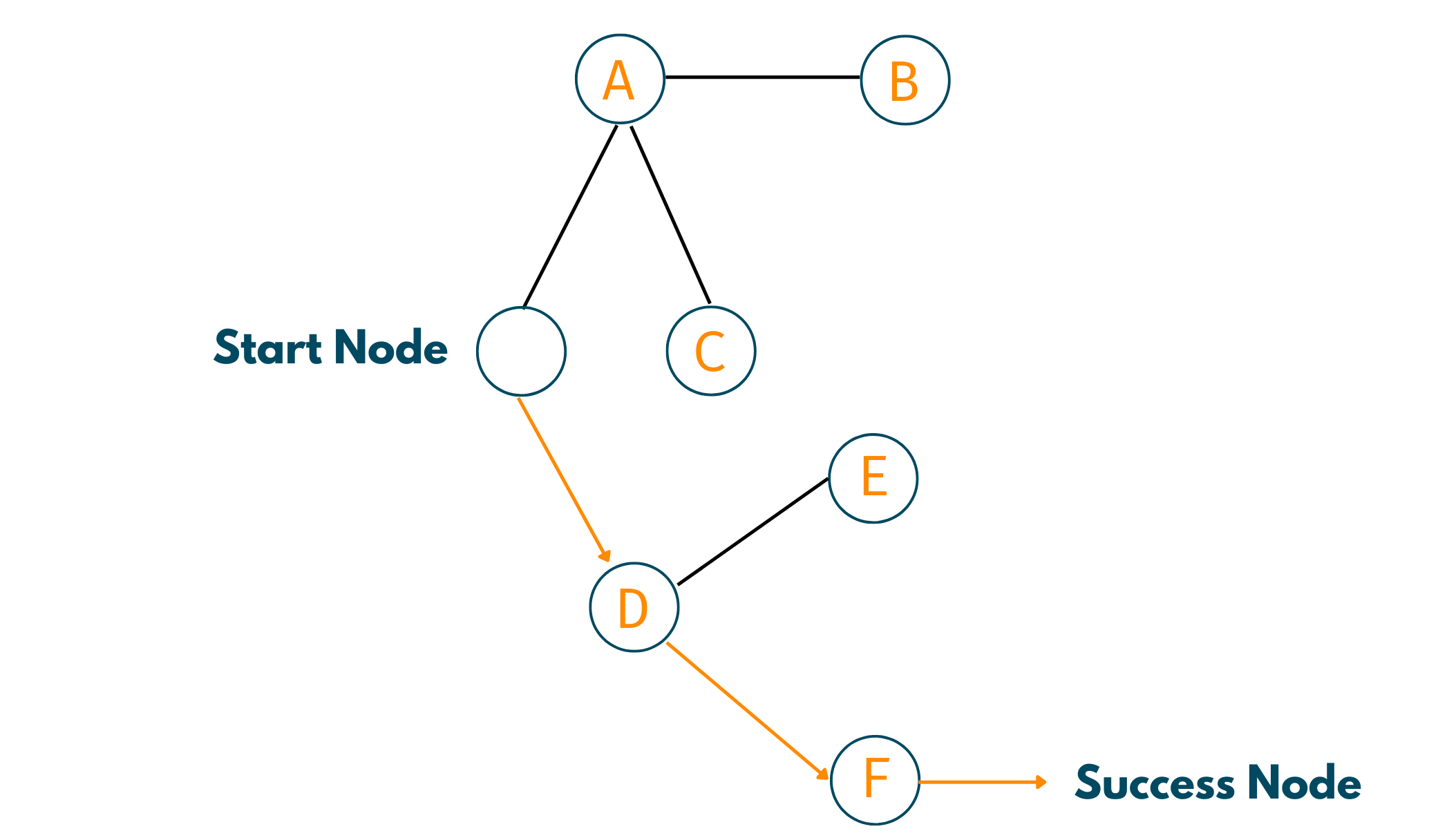
Applications of Backtracking Algorithm
Although we've provided the top 10 questions consisting of backtracking, still here are some applications of this algorithm:
- Graph Coloring
- N-Queens problem
- Hamilton Problem
- Sum of subset
10 Most Asked Backtracking Questions with C++
After getting an understanding of the Backtracking algorithm, you must go through these questions for a better understanding of the concept. So, we have listed below 10 of the most asked questions related to backtracking along with their implementation in C++. So, let's go!
01) Rat in a Maze
Problem Statement: You are given a matrix of order N*N having 1's and 0's written as its elements. Now, imagine that there is a rat at (0,0) and he needs to reach the destination at (N-1, N-1). You need to provide the paths for the rat to reach the destination. Now, 1 means that you can go through the element but 0 means that you cannot. Also, you need to take care of the fact that you can either go up(U), down(D), left(L), or right(R). Print the possible paths.
Approach towards Solution: While working on the solution to this question, make sure to draw a rough sketch of the matrix and enter the elements according to the input. It'll get a lot easier with this. Now, in this question you need to find all the possible paths thus, we'll be using the backtracking approach. The steps are as follows:
- Start with the rat's position (0,0). Now, observe whether you can turn right or you have a 1 below the rat's position. If, at both positions, you have 1, then choose one of the ways.
- Now, start moving by checking where 1 lies from your current position.
- Remember to add the path to your answer. For moving up, you print U, for down, print D, for left, L, and for right, R.
- If at any point you incur a dead end, backtrack to your previous position and again follow a new path.
- If you reach the destination, then print it as the answer and look for other potential answers by repeating the steps.
Example:
Input: N=4; m[][]={{1,0,0,0}, {1,1,0,1}, {1,1,0,0}, {0,1,1,1}}
Output: DDRDRR, DRDDRR
Explanation: Take a look at the below illustration to understand the solution more precisely. Now, you start from (0,0) and see that there is a 1 down. So, you take that path and then move again down as again 1 is present. Now you take a right which is followed by a down and later twice right turns, thus finally reaching the destination. In the same way, you can take another path.

Implementation with C++ Code:
//C++ Program for Rat In A Maze Problem #include<bits/stdc++.h> using namespace std; bool isSafe(int x,int y,int n,int m,vector<vector<int>> &maze,vector<vector<int>> visited){ //Checking our next move is safe by checking if it is present in boundries of maze and not visited and //value of next position should be 1 if((x>=0 && x<n) && (y>=0 && y<m) && visited[x][y] == 0 && maze[x][y] == 1){ return true; } else{ return false; } } void solve(vector<vector<int>> &maze, int n,int m,int x,int y,string path, vector<string>& ans, vector<vector<int>> visited){ //If reach the destination store path in ans and return if(x==n-1 && y==m-1){ ans.push_back(path); return; } //Mark visited where rat is present visited[x][y]=1; //4 directions D/L/R/U where rat can travel //Down int newx=x+1; int newy=y; //Checking if it is safe to go down if(isSafe(newx,newy,n,m,maze,visited)){ //Inserting next direction of rat in path path.push_back('D'); //Function Call solve(maze,n,m,newx,newy,path,ans,visited); //backtracking path.pop_back(); } //UP newx=x-1; newy=y; //Checking if it is safe to go UP if(isSafe(newx,newy,n,m,maze,visited)){ //Inserting next direction of rat in path path.push_back('U'); //Function Call solve(maze,n,m,newx,newy,path,ans,visited); //backtracking path.pop_back(); } //Left newx=x; newy=y-1; //Checking if it is safe to go left if(isSafe(newx,newy,n,m,maze,visited)){ //Inserting next direction of rat in path path.push_back('L'); //Function Call solve(maze,n,m,newx,newy,path,ans,visited); //backtracking path.pop_back(); } //right newx=x; newy=y+1; //Checking if it is safe to go right if(isSafe(newx,newy,n,m,maze,visited)){ //Inserting next direction of rat in path path.push_back('R'); //Function Call solve(maze,n,m,newx,newy,path,ans,visited); //backtracking path.pop_back(); } //marking vis false as we return visited[x][y] = 0; } vector<string> possiblePaths(vector<vector<int>> &maze) { //Size of the maze int n = maze.size(); int m = maze[0].size(); vector<string> ans; //Storing all the paths in ans vector //if starting and end postion value is 0 then we can't have any path if(maze[0][0] == 0 || maze[n-1][m-1]==0){ return ans; } //Starting Position of rat int x =0; int y =0; //Storing the positions where rat is visited vector<vector<int>> visited(n,vector<int>(m,0)); string path = ""; //For storing the path at a time //Function Call solve(maze,n,m,x,y,path,ans,visited); //Return sorted paths sort(ans.begin(),ans.end()); return ans; } int main() { //Inititalizing 2d array which is maze where rat start from (0,0) vector<vector<int>> maze = {{1,0,0,0},{1,1,0,1},{1,1,0,0},{0,1,1,1}}; //Function Call For Storing all the ways to reach at the destination i.e (n-1),(m-1) vector<string> paths = possiblePaths(maze); //Printing the all possible paths to reach destination from (0,0) for(int i=0;i<paths.size();i++){ cout<<paths[i]<<" "; } return 0; }
Output:
DDRDRR, DRDDRR
02) Sudoku Solver
Problem Statement: You are given a Sudoku grid with some empty cells. You need to write a code such that all the cells are filled in a proper fashion according to Sudoku rules which are:
- Each of the digits
1-9must occur exactly once in each row. - Each of the digits
1-9must occur exactly once in each column. - Each of the digits
1-9must occur exactly once in each of the 93x3sub-boxes of the grid.
NOTE: The '.' represents empty space.
Approach towards Solution: If you have solved a Sudoku in real life, it would be very easy for you to understand the problem. The whole point of this problem is to have all the numbers from 1 to 9 in each block, row, and column. So, how do we start with it? Let's see:
- We start with the first row and the first column.
- Start by checking the numbers from 1 to 9.
- If there is a number that is absent from the respective block, column, or row we put that number into that position.
- Repeat the above steps again and again till you fill out the whole box.
- Also, observe that if you make a mistake while filling, you need to backtrack your steps and fill out the position again by checking the vacancy.
Example:
Input:
{{'5','3','.','.','7','.','.','.','.'},
{'6','.','.','1','9','5','.','.','.'},
{'.','9','8','.','.','.','.','6','.'},
{'8','.','.','.','6','.','.','.','3'},
{'4','.','.','8','.','3','.','.','1'},
{'7','.','.','.','2','.','.','.','6'},
{'.','6','.','.','.','.','2','8','.'},
{'.','.','.','4','1','9','.','.','5'},
{'.','.','.','.','8','.','.','7','9'}}
Output:
{{5, 3, 4, 6, 7, 8, 9, 1, 2},
{6, 7, 2, 1, 9, 5, 3, 4, 8},
{1, 9, 8, 3, 4, 2, 5, 6, 7},
{8, 5, 9, 7, 6, 1, 4, 2, 3},
{4, 2, 6, 8, 5, 3, 7, 9, 1},
{7, 1, 3, 9, 2, 4, 8, 5, 6},
{9, 6, 1, 5, 3, 7, 2, 8, 4},
{2, 8, 7, 4, 1, 9, 6, 3, 5},
{3, 4, 5, 2, 8, 6, 1, 7, 9}}
Explanation:
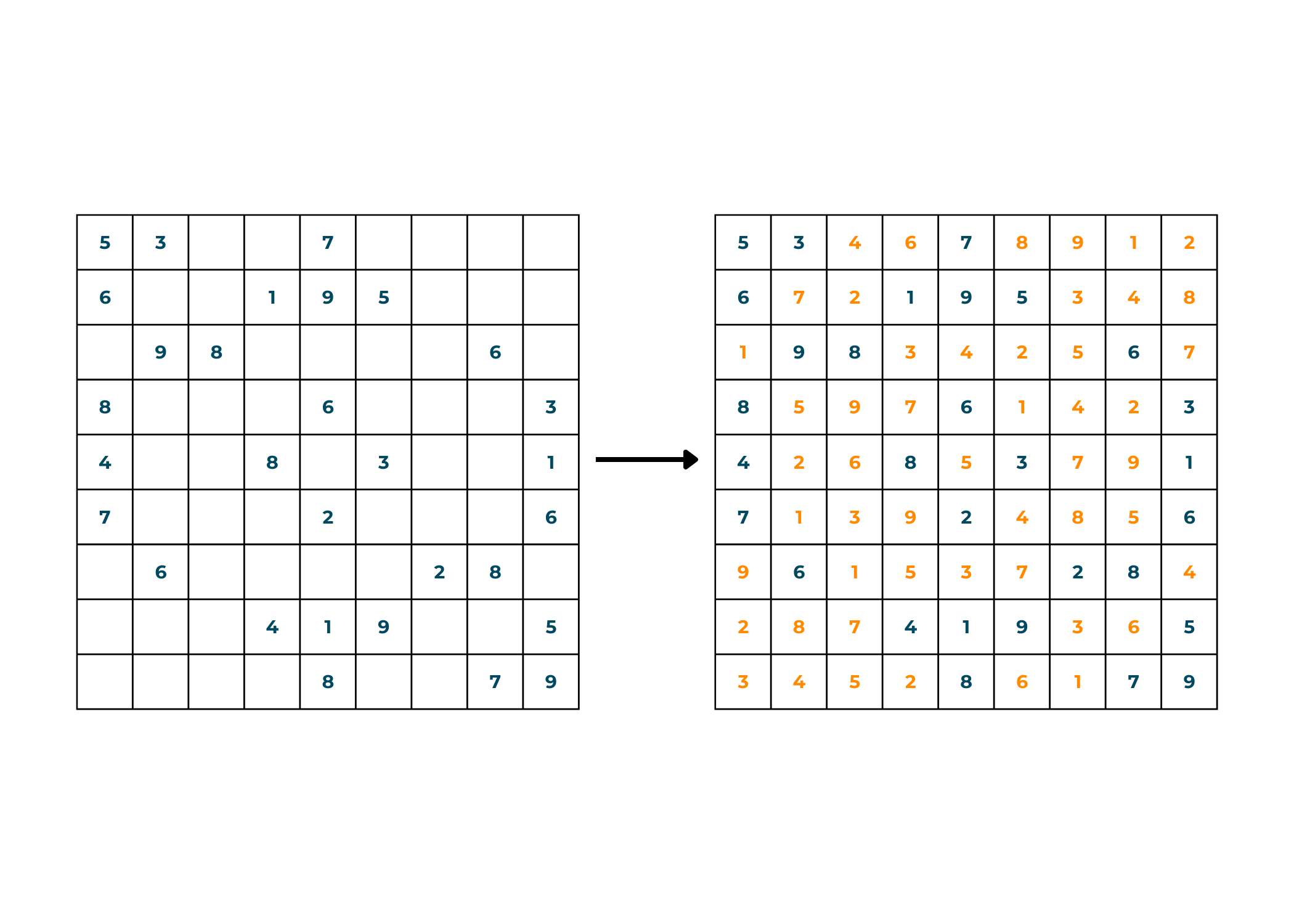
In this example, there is nothing much to explain. Since it is a simple Sudoku solver code that solves the provided matrix as sudoku. You can take a look at the below picture to understand the solution.
Implementation with C++ Code:
//C++ Program For Sudoku Solver Problem #include<bits/stdc++.h> using namespace std; bool isSafe(int row,int col,char val,vector<vector<char>>& board){ //Checking if the val is not present at it's row,col and 3x3 box for(int i=0;i<board.size();i++){ //For checking it's row if(board[row][i]==val) return false; //For Checking it's col if(board[i][col]==val) return false; //For checking it's 3x3 box if(board[3*(row/3) + i/3][3*(col/3)+ i%3]==val) return false; } //If we didn't find val at it's row,col and 3x3 box then return true return true; } bool sudokuSolver(vector<vector<char>>& board){ //Iterating through board from start to end for(int i=0;i<board.size();i++){ for(int j=0;j<board[i].size();j++){ //If we find empty column if(board[i][j]=='.'){ //Check from 1 to 9 value for i,j board for(int k=1;k<=9;k++){ //Check the kth value is safe for the sudoku to complete char num = k+'0'; if(isSafe(i,j,num,board)){ //if it is safe then give the value to that column //And make recursive call for checking sudoku can be solved with that value board[i][j]=num; //Recursive Call bool check = sudokuSolver(board); //If possible then return true and our board will contain our ans if(check){ return true; } else{ // Else do Backtrack board[i][j]='.'; } } } //If we didn't find any ans for i,j column then return false; return false; } } } //return true after iterating through whole board as we didn't find any empty column return true; } int main() { //Initializing the sudoku As a 2d vector board vector<vector<char>> board = {{'5','3','.','.','7','.','.','.','.'}, {'6','.','.','1','9','5','.','.','.'},{'.','9','8','.','.','.','.','6','.'}, {'8','.','.','.','6','.','.','.','3'},{'4','.','.','8','.','3','.','.','1'},{'7','.','.','.','2','.','.','.','6'},{'.','6','.','.','.','.','2','8','.'},{'.','.','.','4','1','9','.','.','5'},{'.','.','.','.','8','.','.','7','9'}}; int n = board.size(); //Function Call For finding Solution of Sudoku bool findSudoku = sudokuSolver(board); //If we can't find find solution of sudoku then if(findSudoku == false) cout<<"Not A Valid Sudoku"; else{ //if we find the solution then print for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ cout<<board[i][j]<<" "; } cout<<endl; } } return 0; }
Output:
5 3 4 6 7 8 9 1 2 6 7 2 1 9 5 3 4 8 1 9 8 3 4 2 5 6 7 8 5 9 7 6 1 4 2 3 4 2 6 8 5 3 7 9 1 7 1 3 9 2 4 8 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 5 2 8 6 1 7 9
03) N-Queens Problem
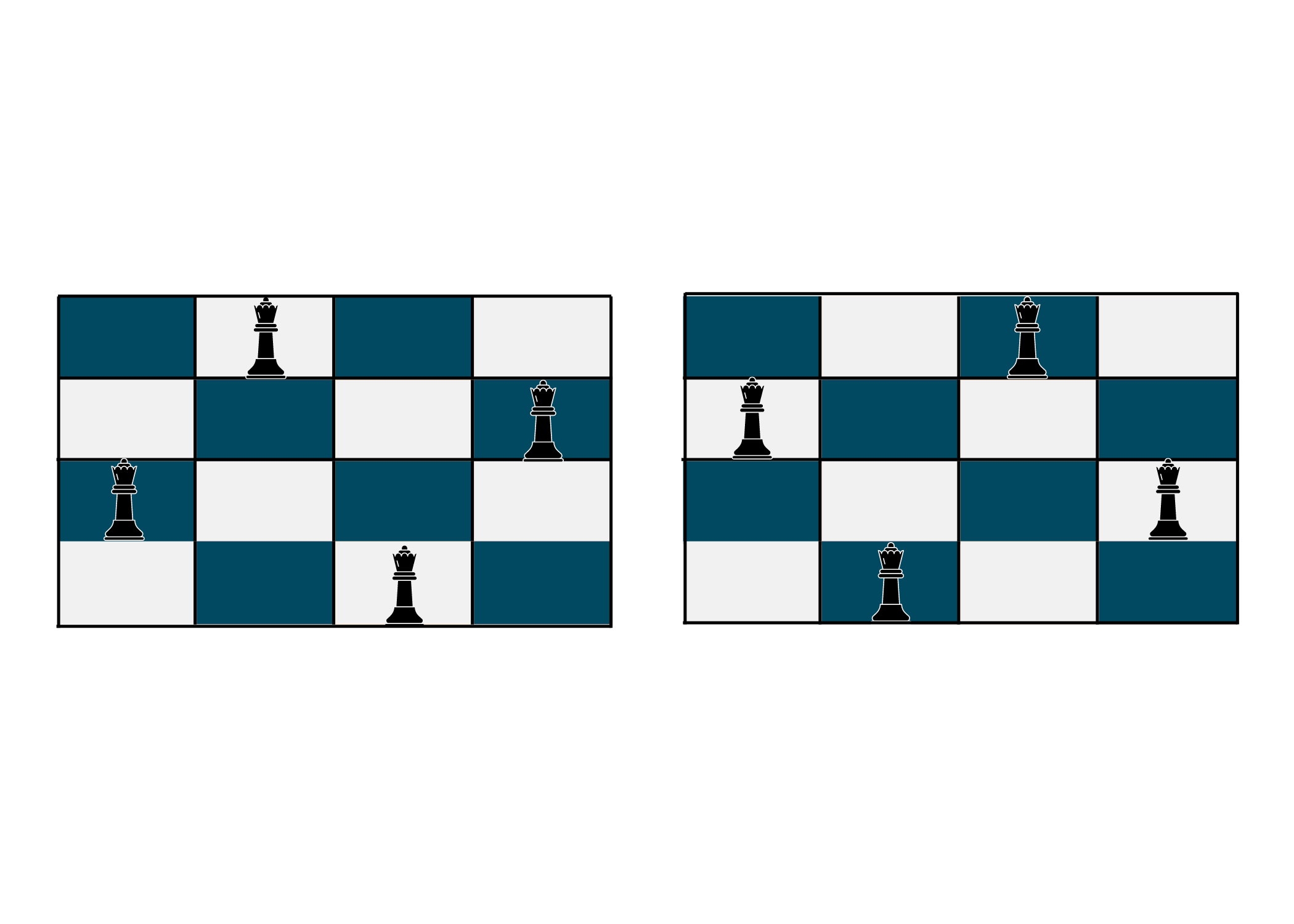
Problem Statement: You are given a chessboard of order n*n and n queens. Now, you have to place the queens in such a position that no queen can attack each other. As per the Chess rules, a Queen can move in any direction that is, forward, backward, left, right, and diagonally. So, you will return the number of possible positions such that the queens can be placed.
Approach towards Solution: For any backtracking question, it is necessary to draw a rough sketch of the question on the paper. This helps you in better visualization of the problem and thus, improved solutions. For solving this question also, make sure to draw a rough sketch and try out all the possible solutions.
- Start by putting the first queen in its position.
- Now, check on which places you can put the second queen.
- If you cannot find any suitable place for the third queen, backtrack your steps and reorganize the positions for your queens.
- Repeat these steps until you find a suitable place for all the n queens given to you.
Example:
Input: n=4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
*The '.' represent the empty spaces.
Explanation: We start by putting the queens one by one on the chessboard. If at any time, a queen cannot be placed, we change the other queens' location and reorganize them using backtracking. Look at the below illustration to understand.
//C++ Program for N Queen Problem #include<bits/stdc++.h> using namespace std; void addSolution(vector<vector<string>>& ans,vector<vector<char>>& board,int n){ //In this we store the possible solution into answer //Initialising the temp for storing a possible solution vector<string> temp(n); //Looping from 0th row to nth row for(int i=0;i<n;i++){ //index of the temp array int k=0; //Looping from 0th col to nth col for(int j=0;j<n;j++){ //Adding elements into temp array temp[k++] += board[i][j]; } } //Adding temp vector into answer ans.push_back(temp); } bool isSafe(int row,int col,vector<vector<char>>& board,int n){ //In this we check only left side of the queen that there is any other queen present on the left //Where they can attack each other //First we check on the left horizontal line from the queen int x = row; int y = col; //this is done by only decrementing by y only with 1 and checking if queen is present while(y>=0){ if(board[x][y]=='Q'){ return false; } y--; } //Secondly we check the Upward left diaganol from the queen y=col; x=row; //this is done by only decrementing by y only with 1 and x by 1 also while(x>=0 && y>=0){ if(board[x][y]=='Q') return false; x--; y--; } //Lastly we check the downward left diaganol from the queen y=col; x=row; //this is done by only decrementing by y only with 1 and incrementing x by 1 while(x<n && y>=0){ if(board[x][y]=='Q') return false; x++; y--; } //Returning true at last if we doesn't fail in between return true; } void solve(int col,vector<vector<string>>& ans,vector<vector<char>>& board,int n){ //If we are at the outside the last column then add the solution to our ans array if(col==n){ addSolution(ans,board,n); return; } //Looping through row where we can placed queens for(int row=0;row<n;row++){ //checking if it is safe to placed the queen on ith row if(isSafe(row,col,board,n)){ //If it safe then place queen at that position and make recursive call for next queen board[row][col]='Q'; //Recursive call for next queen to be placed at next column so increment column solve(col+1,ans,board,n); //Backtracking to find another solution board[row][col]='.'; } } } vector<vector<string>> solveNQueens(int n) { //Initialising chessboard vector<vector<char>> chessboard(n,vector<char>(n,'.')); //Storing the distinct solutions vector<vector<string>> ans; //Function Call solve(0,ans,chessboard,n); return ans; } int main() { //Inititalizing the total No.of Queens we have and //This will be also the size of the chessboard int n = 4; //Function Call For placing N Queens on chessboard so that no 2 queens attack each other vector<vector<string>> ans = solveNQueens(n); //Printing all the distinct position where queens can be placed cout<<"The distinct solution of N Queen Puzzle are :"<<endl; for(int i=0;i<ans.size();i++){ cout<<"["; for(auto s:ans[i]){ cout<<s<<" "; } cout<<"] "; } return 0; }
Output:
The distinct solution of N Queen Puzzle are :
[.Q.. ...Q Q... ..Q. ] [..Q. Q... ...Q .Q.. ]
Here is a complete guide to N Queen Problem to dive deep into it.
04) Array Permutations
Problem Statement: You are given an array with certain elements. You need to return an array that consists of all the possible permutations of the elements present in the inputted array. Permutation refers to the arrangement of objects.
Approach towards Solution: So, in this question, you are required to return all the possible permutations of the array elements. What does that mean? This means that whatever array of elements you are provided with, you need to return all the possible arrangements of it in form of an array.
- Take the elements and start making random arrangements with them.
- If, the arrangement is a new one, add it to the list of your solution.
- If it is not, discard it and move on to the next possible one.
Example:
Input: {1,2,3,4}
Output: Permutations of {1,2,3,4} are :
{ [ 1 2 3 4 ] , [ 1 2 4 3 ] , [ 1 3 2 4 ] , [ 1 3 4 2 ] , [ 1 4 3 2 ] , [ 1 4 2 3 ] , [ 2 1 3 4 ] , [ 2 1 4 3 ] , [ 2 3 1 4 ] , [ 2 3 4 1 ] , [ 2 4 3 1 ] , [ 2 4 1 3 ] , [ 3 2 1 4 ] , [ 3 2 4 1 ] , [ 3 1 2 4 ] , [ 3 1 4 2 ] , [ 3 4 1 2 ] , [ 3 4 2 1 ] , [ 4 2 3 1 ] , [ 4 2 1 3 ] , [ 4 3 2 1 ] , [ 4 3 1 2 ] , [ 4 1 3 2 ] , [ 4 1 2 3 ]}
Explanation: We didn't do anything except the steps that have already been mentioned above.
Implementation with C++ Code:
//C++ Program to Array Permutations #include<bits/stdc++.h> using namespace std; void solve(vector<int>& nums,int index,vector<vector<int>>& ans){ //If index is equal to size of num then store our num vector in ans and return if(index>=nums.size()){ ans.push_back(nums); return; } //Looping from index till size of the array for(int i=index;i<nums.size();i++){ //Swap the ind and ith numbers in nums array swap(nums[index],nums[i]); //Recursive Call with increase in the index solve(nums,index+1,ans); //backtracking swap(nums[index],nums[i]); } } vector<vector<int>> arrayPermutations(vector<int>& nums) { //Initializing answer vector where we store permutations vector<vector<int>> ans; int index = 0; //ind of the starting point //Function Call solve(nums,index,ans); return ans; } int main() { //Inititalizing array vector<int> arr = {1,2,3,4}; //Function Call vector<vector<int>> permutations = arrayPermutations(arr); //Printing the permutations of vector arr cout<<"Permutations of {1,2,3,4} are : "<<endl; for(int i=0;i<permutations.size();i++){ cout<<" [ "; for(int j=0;j<permutations[i].size();j++){ cout<<permutations[i][j]<<" "; } if(i!=permutations.size()-1) cout<<"] ,"; } cout<<"]"; return 0; }
Output:
Permutations of {1,2,3,4} are :
[ 1 2 3 4 ] , [ 1 2 4 3 ] , [ 1 3 2 4 ] , [ 1 3 4 2 ] , [ 1 4 3 2 ] , [ 1 4 2 3 ] , [ 2 1 3 4 ] , [ 2 1 4 3 ] , [ 2 3 1 4 ] , [ 2 3 4 1 ] , [ 2 4 3 1 ] , [ 2 4 1 3 ] , [ 3 2 1 4 ] , [ 3 2 4 1 ] , [ 3 1 2 4 ] , [ 3 1 4 2 ] , [ 3 4 1 2 ] , [ 3 4 2 1 ] , [ 4 2 3 1 ] , [ 4 2 1 3 ] , [ 4 3 2 1 ] , [ 4 3 1 2 ] , [ 4 1 3 2 ] , [ 4 1 2 3 ]
05) M Coloring Problem
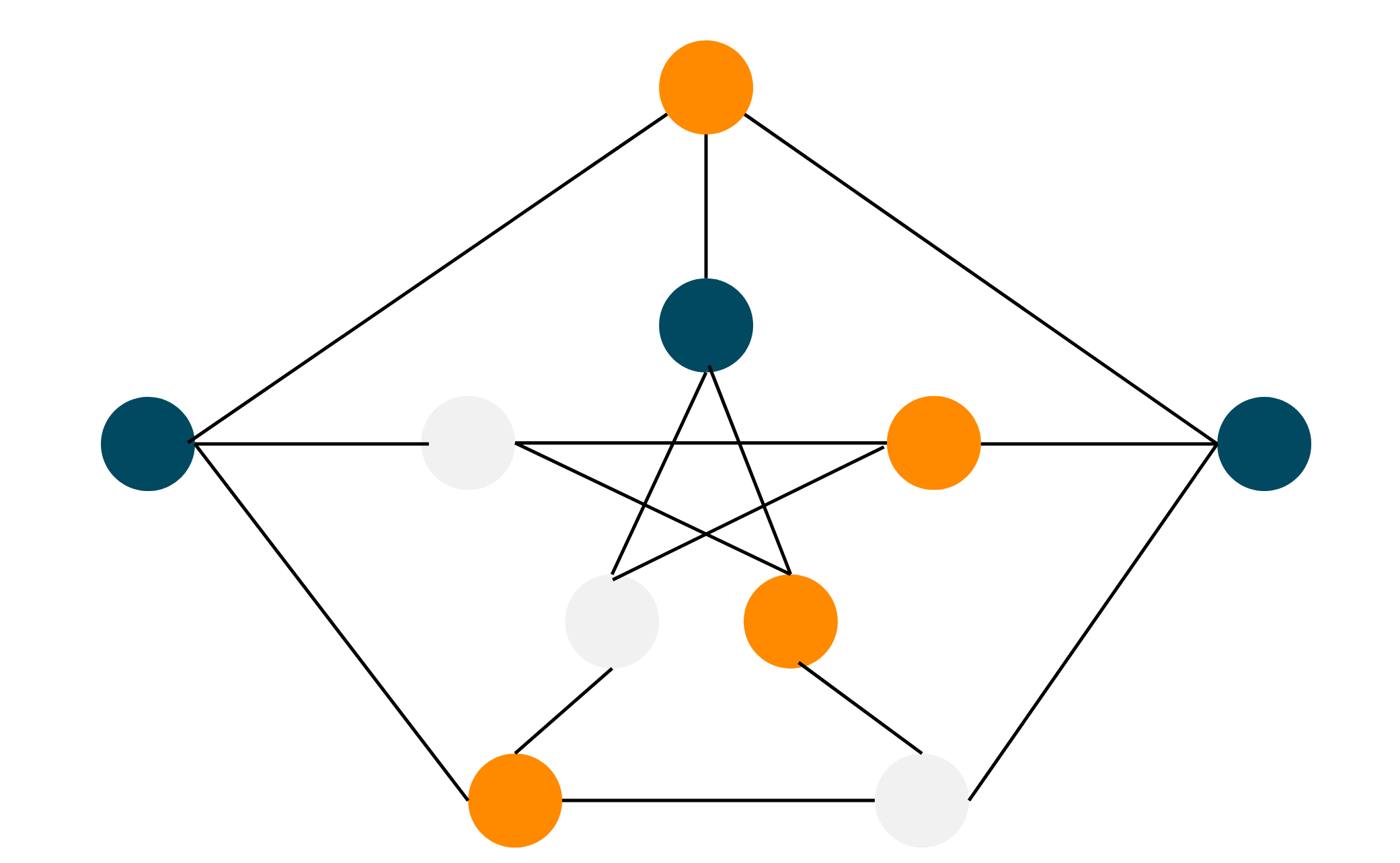
Problem Statement: You are given an undirected graph and an integer m. You need to check whether the graph can be colored with m colors with no two adjacent edges being of the same color. Coloring a graph means assigning different colors to the vertices.
Approach towards Solution: Now, you need to check whether the vertices can be colored in m colors with no adjacent edges being of the same color. So, the optimal way to try it out is to assign colors one by one to all the vertices and check whether they satisfy the provided configuration. Follow the below steps:
- Start by assigning the first vertex with a color.
- Now, move to the next one and assign a different color to it.
- Check whether it satisfies the configuration or not.
- If it does, keep on moving otherwise discard it.
Example:
Input: m=3; {{ 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }}
Output: It is possible to color vertices.
Explanation: We start by assigning the first vertex color and later, move on to assigning others as well. We keep on checking whether the configuration is satisfactory or not. For a better explanation, you can check out the below illustration.
Implementation with C++ Code:
//C++ Program For M-Coloring Problem #include <bits/stdc++.h> using namespace std; bool isPossible(int node,int col,int n,vector<int>& color,bool graph[4][4]){ //Looping through each node for(int k=0;k<n;k++){ //Check if the node is not equal to kth node //Check if kth node and node is adjacent node //then check if kth node color is equal to given color //if yes then return false else continue if(k!=node && graph[k][node]==1 && color[k]==col){ return false; } } //If we doesn't find any same color allocated to it's adjacent node then return true return true; } bool solve(int node,int m,int n,vector<int>& color,bool graph[4][4]){ //If we traverse all node then return true if(node==n) return true; //Allocating color to the node from 1 to m for(int i=1;i<=m;i++){ //if we find color of node where it's adjacent node doesn't contain that color //then allocate that color to node and make recursive call for next node //if it's doesn't return true then backtrack then check by allocating next color if(isPossible(node,i,n,color,graph)){ color[node] = i; //Recursive Call if(solve(node+1,m,n,color,graph)) return true; //Backtrack color[node] = 0; } } //If we didn't return true in allocating color //then return false return false; } int main() { //Total nodes in graph int n = 4; //Implementing graph where indexes of two nodes is true if connected to each other bool graph[4][4] = { { 0, 1, 1, 1 }, { 1, 0, 1, 1 }, { 1, 1, 0, 0 }, { 1, 1, 0, 0 }, }; //total colors 'm' to be 3 int m =3; //For storing the color of each node vector<int> color(n,0); //Printing is it possible to colour vertices where //no two adjacent vertices of the graph are colored with the same color if(solve(0,m,n,color,graph)){ cout<<"It is possible to color vertices"<<endl; } else{ cout<<"It is not possible to color vertices"<<endl; } return 0; }
Output:
It is possible to color vertices
06) Letter Combinations of a Phone Number
Problem Statement: You are given a string of certain numbers from 2-9. You have to return all the possible combinations that could be made using the letters they represent. Check out the image below:

Approach towards Solution: As you have already seen the image, you may be having a little idea of what you have to do. Now, how to start with the solution? You should be well aware of which number contains which letters. After this, you should take the first digit from the input and start printing the pairs one by one that could be made using that digit and the digit following it. Keep on repeating the same steps for all the digits present in the input and you'll get the answer. The steps are as follows:
- Observe which alphabets are related to which numbers.
- Now, start mapping the alphabets of the first digit with the alphabets contained by the next digit.
- Keep printing the mapped pairs and traverse to all the input digits.
- Return the answer.
Example:
Input: "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
Explanation: Here, we were given 2 digits, 2 and 3. Now, 2 has letters a, b, c and 3 has letters d, e, f. So, we make pairs as 'ad', then 'ae' and similarly all the others.
Implementation with C++ Code:
//C++ Program For Letter Combinations of a Phone Number #include<bits/stdc++.h> using namespace std; void solve(string digits, string temp, int ind, vector<string>& ans, string mapping[]){ //if we traverse all index of digits if(ind>=digits.length()){ //store the temp string in ans vector and return ans.push_back(temp); return; } //Find the number at ind of digits int element = digits[ind] - '0'; //string at that number on phone can be find out in mapping string s = mapping[element]; //Looping through string for(int j=0;j<s.length();j++){ //Inserting the jth index of string temp.push_back(s[j]); //Recursive call for next index of digits solve(digits,temp,ind+1,ans,mapping); //Backtracking to remove the last elment in temp string temp.pop_back(); } } vector<string> letterCombinations(string digits) { vector<string> ans; //Storing ans in this vector //if there is no digit then return empty vector if(digits.length()==0){ return ans; } //temp string for storing each ans string temp=""; //Mapping of digits to letters string mapping[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; //Function Call solve(digits,temp,0,ans,mapping); //Return ans return ans; } int main() { //Initializing string of digits whom which we have to find combinations on phone string digits = "234"; //Function Call vector<string> ans = letterCombinations(digits); //Printing the letter combinations cout<< "All possible letter combinations of Digits 234 are :"<<endl; for(int i=0;i<ans.size();i++){ cout<<ans[i]<<" "; } }
Output:
All possible letter combinations of Digits 234 are : adg adh adi aeg aeh aei afg afh afi bdg bdh bdi beg beh bei bfg bfh bfi cdg cdh cdi ceg ceh cei cfg cfh cfi
07) Partition Palindrome
Problem Statement: You are given a string. You need to return all the partitions of the string that are palindromic in nature. A palindrome is a word, phrase, or set of digits that reads the same as backward and forwards.
Approach towards Solution: Here, you need to find all the possible palindromes in the given string. So this is how you approach the solution:
- Start by partitioning every single alphabet of the given string into palindromes of length 1.
- Now, expand the smaller palindromes into bigger ones by joining one or two letters every time and simultaneously checking if that ends up in a palindrome.
- Keep printing the palindromes and if no palindrome can be created then return the single alphabet each time.
Example:
Input: "nitin"
Output: "n i t i n", "n iti n", "nitin"
Explanation: We split each and every letter of the inputted string and start by expanding the smaller palindromes into bigger ones.
Implementation with C++ Code:
//C++ Program For Palindrome Partition #include<bits/stdc++.h> using namespace std; //Checking the string is palindrome from start to end bool isPalindrome(string s,int start,int end){ //Looping while start is less than end while(start<=end){ //if start value is not equal to end value then return false if(s[start]!=s[end]){ return false; } //Updating start and end end--; start++; } //return true if we traverse through string without returning false return true; } void solve(string s,int index,vector<string>& temp,vector<vector<string>>& ans){ //Base Case if we traverse all index of string s //then insert the temp vector into ans if(index == s.length()){ //Inserting temp vector in ans and returning ans.push_back(temp); return ; } //Looping through string s from index for(int i=index;i<s.length();i++){ //Checking if index to i string is palindrome if(isPalindrome(s,index,i)){ //If index to i string is palindrome then insert in temp vector temp.push_back(s.substr(index,i-index+1)); //Recursive Call for finding next palindrome solve(s,i+1,temp,ans); //Backtracking temp.pop_back(); } } } int main() { //string s for finding it's all partition palindrome string s = "aabac"; //Storing answer in ans vector vector<vector<string>> ans; //Temperory vector for storing each answer vector<string> temp; int index =0; //starting index //Function Call solve(s,index,temp,ans); //Printing all the partition palindrome of string s for(int i=0;i<ans.size();i++){ for(int j=0;j<ans[i].size();j++){ cout<<ans[i][j]<<" "; } cout<<endl; } return 0; }
Output:
a a b a c a aba c aa b a c
08) Combinations
Problem Statement: You are given 2 integers n and k. You need to return all the combinations of k digits from the range 1 to n. NOTE: Combinations having the same digits are not considered again and again. For eg. (1,2) and (2,1) are treated as the same.
Approach towards Solution: This problem is quite simple if you think a bit logically. Now, from the n numbers, you have to find various combinations consisting only of k digits. Follow this:
- Observe the inputted integers.
- Now, n means that the numbers from 1 to n can be included. So, you need to list all the numbers in the range of 1 to n.
- After this, start pairing different numbers one by one in pairs of k digits.
- You will get your answer by combining all the pairs.
Example:
Input: n = 4; k = 2
Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Explanation:
We are given a range of 1 to 4. Now, we lay out all the numbers in this range that is, 1,2,3, and 4. After this, we'll make pairs of 2(k=2) and print out all the answers.
Implementation with C++ Code:
//C++ program for Combinations #include<bits/stdc++.h> using namespace std; void solve(vector<int>& temp,vector<vector<int> >& ans,int start,int num,int n, int k){ //Base case if length temp is k then insert into ans and return if(num==k){ ans.push_back(temp); return ; } //Looping through start to n for(int i=start;i<n;i++){ //inserting i+1 into temp temp.push_back(i+1); //Recursive Call solve(temp,ans,i+1,num+1,n,k); //Backtracking by removing last element of temp temp.pop_back(); } } vector<vector<int>> combinations(int n, int k) { //temporary vector to store each combination vector<int> temp; vector<vector<int> > ans; //storing all combinations //Function call solve(temp,ans,0,0,n,k); return ans; } int main() { int n = 4; //Range of numbers in combinations to be [1,n] int k=2; //Size of each combination to be 2 //Function Call vector<vector<int>> ans = combinations(n,k); //Printing all possible combinations of k numbers chosen from the range [1, n] for(int i=0;i<ans.size();i++){ cout<<"["; for(int j=0;j<ans[i].size();j++){ if(j==ans[i].size()-1) cout<<ans[i][j]; else cout<<ans[i][j]<<","; } cout<<"]"<<" "; } return 0; }
Output:
[1,2] [1,3] [1,4] [2,3] [2,4] [3,4]
09) Combination Sum
Problem Statement: You are given an array of integers 'candidates' and an integer 'target'. You have to find out all the possible combinations of 'candidates' elements that sum to give 'target'. You may use the element in 'candidate' any number of times.
Approach towards Solution: You need to give as many combinations as possible. So lay out the elements of the given array. Try to find out combinations that can sum up to give the target. Remember that you can also repeat the elements as many times as you want.
- Begin by repeating the single elements of the array, to sum up, and give the target as the answer.
- After this, move on to pairing them with each other to find potential answers.
- Now, if you encounter a dead end, backtrack your solution to the previous digit and start off again.
Example:
Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]
Explanation: Since the target is an even number, you observe that the first element of array is even, so you print it the required number of times to provide target. Later, we move on to pairing other elements one by one and find out the potential combinations.
Implementation with C++ Code:
//C++ program for Combination Sum #include<bits/stdc++.h> using namespace std; void solve(vector<int>& candidates, int target, int ind, vector<int>& output, vector<vector<int>>& ans){ //base case if we traverse all candidates if(ind == candidates.size()){ //if target is zero then //insert output array into ans and return if(target==0) ans.push_back(output); return ; } //include candidates of index if target is greater than candidate[ind] if(candidates[ind]<=target){ //insert ind of candidates in output output.push_back(candidates[ind]); //Recursive call by only updating target //We will not update ind as same number can be use multiple times solve(candidates,target-candidates[ind],ind,output,ans); //Backtracking by removing last element output.pop_back(); } //excluding current index and moving to next index solve(candidates,target,ind+1,output,ans); } vector<vector<int>> combinationSum(vector<int>& candidates, int target) { vector<vector<int>> ans; //storing answer of unique combinations vector<int> output; //storing answer at a instance int ind = 0; //starting index //Function Call solve(candidates,target,ind,output,ans); return ans; } int main() { //Array of candidates whose combinations sum to be equal to target vector<int> candidates = {2,3,4,5}; int target = 7; //target of each combination sum //Function Call vector<vector<int>> ans = combinationSum(candidates,target); //Printing all unique combinations of candidates for(int i=0;i<ans.size();i++){ cout<<"["; for(int j=0;j<ans[i].size();j++){ if(j==ans[i].size()-1) cout<<ans[i][j]; else cout<<ans[i][j]<<","; } cout<<"]"<<" "; } return 0; }
Output:
[2,2,2,2] [2,2,4] [2,3,3] [3,5] [4,4]
10) Word Search
Problem Statement: You are given a grid of m*n order having various alphabets as its elements. You are also given a word. You need to check whether the given word exists in the word matrix or not. Take a look at the below illustration to understand what type of grid you may encounter.

Approach towards Solution: Most of the programming questions are related to daily life. You should solve this question as if you're solving the word search game physically. Now follow the same mentality and the steps:
- Observe which word and elements you have been given.
- Now, begin by finding out the elements from the 0th index.
- At any time, if you cannot locate a particular element in the grid, return false.
- If, till the end, you find all the letters of the target word, then return true.
Example:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: Yes, the word exists on the board.
Explanation: We start off with the first letter and upon finding it, we iterate among the rest of the letters and find them all. Below is an illustration of the same.

Implementation with C++ Code:
//C++ program for Word Search #include<bits/stdc++.h> using namespace std; bool dfs(int i,int j,vector<vector<char>>& board,string word){ //if word length is zero then return true if(word.length()==0){ return true; } //if index of boards are out of boundary or board[i][j] is not equal to first char of word //then return false as we cannot traverse further if(i<0 || j<0 || i>=board.size() || j>=board[0].size() || board[i][j] != word[0]){ return false; } //updating board[i][j] to mark it visited board[i][j] = '*'; //removing first element of word and store it in new string string s = word.substr(1); //check for 4 directional adjacent neighbours if anyone return true then we find the word in board //and updating word to new string s in recursive call bool flag = dfs(i+1,j,board,s) || dfs(i,j+1,board,s) || dfs(i,j-1,board,s) || dfs(i-1,j,board,s); //Backtracking board[i][j] = word[0]; //returning true if we find word otherwise false return flag; } bool wordSearch(vector<vector<char>>& board, string word) { //Traversing through whole board while we didn't find word for(int i=0;i<board.size();i++){ for(int j=0;j<board[i].size();j++){ //function call to search word //if we find then return true if(dfs(i,j,board,word)){ return true; } } } //If we didn't find word in board after traversing then return false return false; } int main() { //Initializing 2d board which contains letter vector<vector<char>> board = {{'A','B','C','E'},{'S','F','C','S'},{'A','D','E','E'}}; string word = "ABCCED"; //string we have to find in board //Function Call and returning answer if(wordSearch(board,word)){ cout<<"Yes, word exists in board"; } else{ cout<<"No, word does not exist in board"; } return 0; }
Output:
Yes, word exists in board
Conclusion
Backtracking is certainly a complex topic and its problems are even more complex. But, the key point is to keep practicing and work hard in solving these questions. After understanding the above questions, you can certainly move to harder problems and find their solutions. If you encounter any doubts, FavTutor is here to help you solve your doubts 24*7.