Bucket Sort in C++ (Code with Example)

Sorting is a very important part of problem-solving as well as many real-world applications. There are a bunch of different sorting algorithms available with each having its own purpose and use case. Let us get an insight about one such sorting algorithm known as Bucket sort in this article. Before that let's get into the explanation of sorting.

What is Sorting? 

Sorting is a way of bringing some orderliness in the data. Let us understand the term better with an application which we use in our daily life, that is our phone contact list, the names are arranged alphabetically in our phone, which is one of the applications of sorting. So, we can state that Sorting is a technique of organizing the data or arranging the records either in ascending or descending order. The efficiency of a sorting technique depends on memory utilization, the time required to sort the elements, utilization of processors, etc. 

What is Bucket sort?

Bucket sort is a kind of sorting algorithm, which sorts the elements by grouping them into lists based on digits. Since the elements are grouped and put together in a specific list, this algorithm is known as Bucket sort. Since it groups based on the number of digits it is also known as radix sort or digital sort. This algorithm sorts the list by following the order starting from the least significant digit and continues upto most significant digit. The number of iterations is determined by the element with high digits.

Algorithm for bucket sort

Step 1: To know the number of passes required first find the maximum element of the list and calculate its number of digits.

Step 2: Initialise buckets for all the digits starting from 0 to 9

Step 3: Perform sorting by initially considering the least significant bit (LSB) i.e., one's digit, and insert the digit value in the respective bucket. for example, if LSB is 4 then the key is inserted in the 4th bucket, if it is 2 then the digit value is inserted in the 2nd bucket.

Step 4: Now perform sorting by considering the second last digit and inserting the values in the respective bucket. Step 5: Repeat steps (4) and (5) for all the digits the digits are examined.

Example for bucket Sort

To understand the approach of bucket sort, let us consider an example and look into steps that are performed to sort the elements.

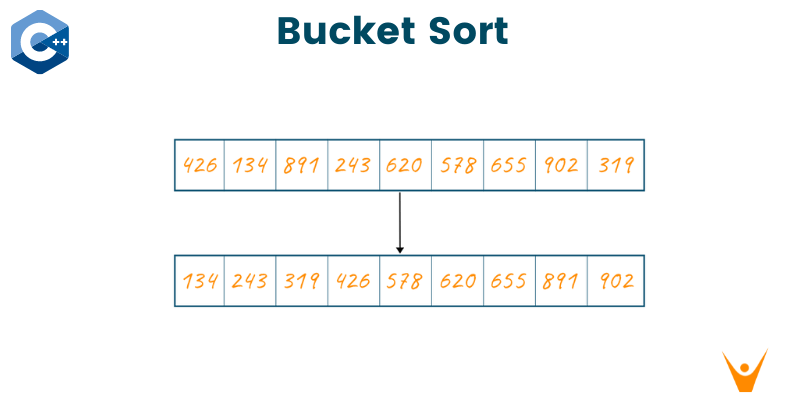
The input array we consider as an example is {426, 134, 891, 243, 620, 578, 655, 902, 319}. Since the largest elements contain three digits the total pass in the algorithm will be 3.

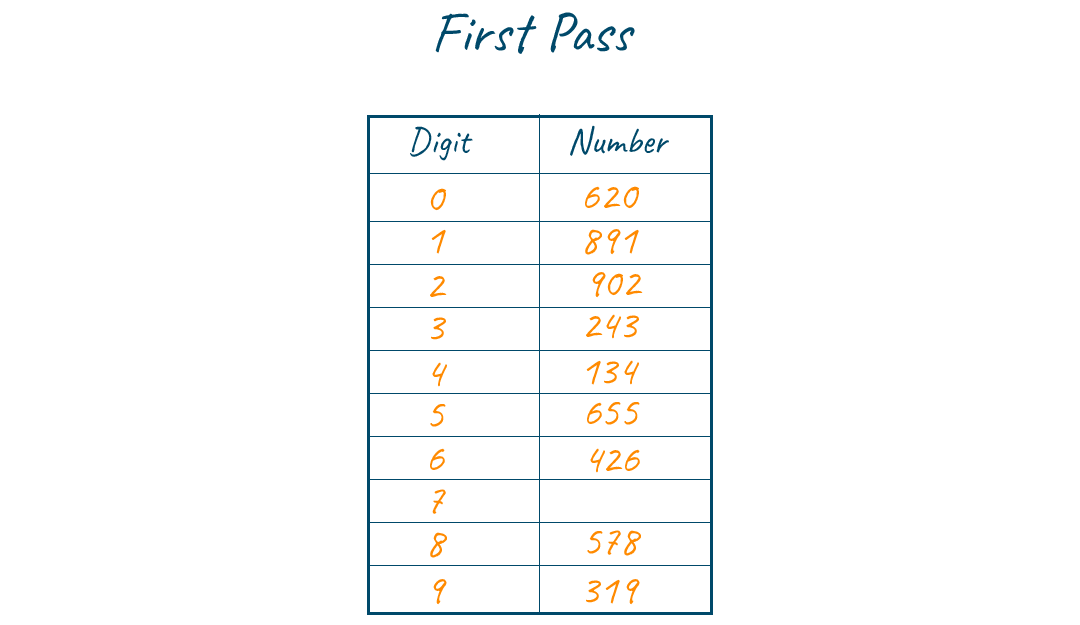
Consider the nth digit which is the last digit (Least significant digit) of all keys and put them into their corresponding bins. Now, remove key from the queue and append them in order to the list. The list of elements after grouping the numbers based on last digit is {620,891,902,243,134,655,426,578,319}.

Consider (n-1)th digit that is the second digit of all keys and put them into their corresponding bins. Now, remove keys from the queue and append them in order to the list. The list of elements after grouping the numbers based on second digit is {902, 319, 426, 620, 134, 243, 655, 578, 891}.

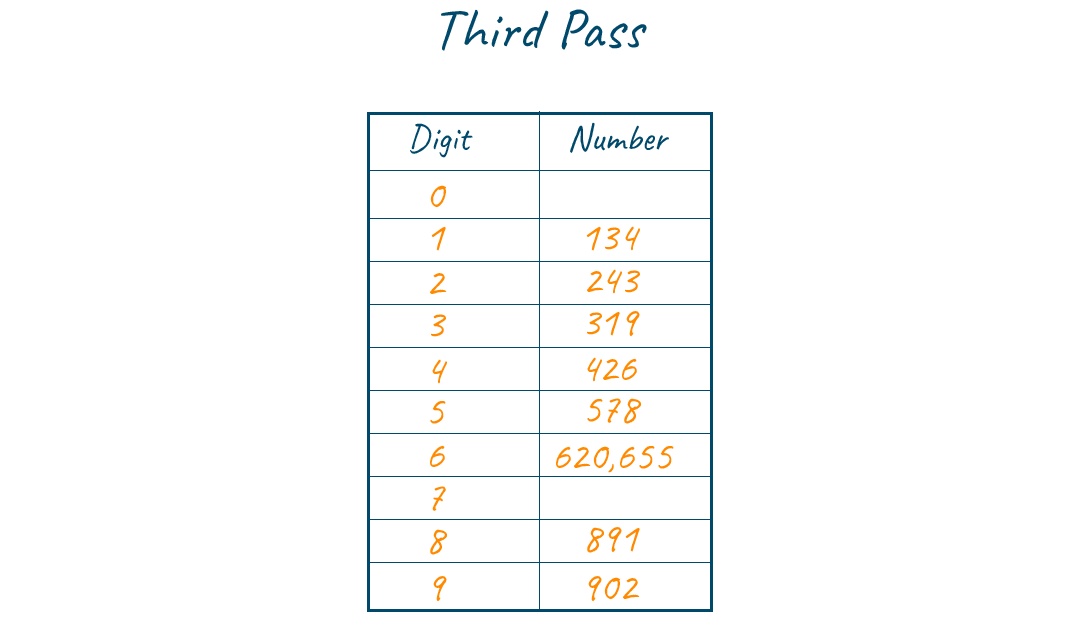
Consider (n-2)th digit that is the first digit of all keys and put them into their corresponding bins. Now, remove keys from the queue and append them in order to the list. The list of elements after grouping the numbers based on the first digit is {134, 243, 319, 426, 578, 620, 655, 891, 902}. And hence we have sorted the array with three passes.

Sorted array 

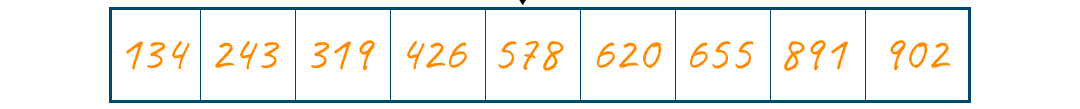
C++ Code for Bucket Sort

The following code shows the implementation of bucket sort in C++.

#include
using namespace std;
int findMax(int arr[], int n)
{
    int i,max=arr[0],cnt=0;
    for(i=1;i<n;i++)
    {
        if(arr[i]>max)
            max=arr[i];
    }
    while(max>0)
    {
        cnt++;
        max=max/10;
    }
   
    return cnt;
}

void bucketSort(int arr[],int *bucket[],int n)
{
    static int i,j[10],k,l,d=1;
    int c;
    c=findMax(arr,n);
  
    for(int m=0;m<c;m++)
    {
        for(i=0;i<10;i++)
            j[i]=0;
        for(i=0;i<n;i++)
        {
            k=(arr[i]/d)%10;
            bucket[k][j[k]]=arr[i];
            j[k]++;
        }
     
        l=0;
        for(i=0;i<10;i++)
        {
            for(k=0;k<j[i];k++)
            {
                arr[l]=bucket[i][k];
                l++;
            }
        }
        d*=10;
    }
}
int main()
{
    int n,*arr,i;
    int *bucket[10];
    cout<<"Enter no of element : ";
    cin>>n;
    arr=new int[n+1];
    for(i=0;i<10;i++)
        bucket[i]=new int[n];
    cout<<"Enter array element : ";
    for(i=0;i<n;i++)
        cin>>arr[i];
    bucketSort(arr,bucket,n);
   
    cout<<"Sorted array : ";
    for(i=0;i<n;i++)
        cout<<arr[i]<<" ";
    return 0;
}

Output

Enter no of element : 4
Enter array element : 7
2
5
4
Sorted array : 2 4 5 7 

Time complexity

Usually, the best-case scenario for a comparison-based sorting algorithm will be O(nlogn). But bucket sort can be implemented with a linear time complexity in the best case i.e., O(n). The average time complexity will be O(n+k).

Space Complexity

The space complexity for bucket sort will be O(n * k). The space complexity is quite high when compared to other sorting algorithms since the use of buckets.

Advantages of Bucket sort

• It is simple and performs faster computation for numbers or strings
• Bucket sort can be used as an external sorting algorithm. 
• Once the list is grouped in buckets then it can be processed independently.

Disadvantages of Bucket sort

• Consuming more space when compared to other algorithms is the major drawback of this algorithm
• The efficiency of this algorithm is completely dependent on the distribution of the data. If the data is distributed not in a uniform way, then the performance of the algorithm will be poor.

Applications of Bucket sort

1. Bucket sort is mostly used when the data contains floating-point values.
2. When the data is uniformly distributed in a specific range then bucket sort will be a perfect option to use.

Conclusion

There are a lot of pre-built sorting functions available for us to use. But understanding the approach of some important sorting algorithms is necessary for logic building and problem-solving. We have discussed bucket sort with code in this article. If you are interested in sorting algorithms, then check out our articles on quicksort, bubble sort, and merge sort.