With over 44 Zettabytes of data available over the internet, the need to search for the right information becomes of utmost importance. That is the main reason pattern searching algorithms are being asked more frequently in the interviews of product-based companies.
We, at FavTutor, realize this, and so, after covering Boyer-Moore Algorithm and Rabin-Karp Algorithm, we should learn about Aho-Corasick Algorithm. In this tech blog, we'll understand how this algorithm works with an example, and its implementation in 3 programming languages including Java, C++, and Python.
What is Aho-Corasick Algorithm?
Proposed in 1975, by Alfred Aho and Margaret Corasick, Aho-Corasick Algorithm is considered to be a much more efficient approach while searching for a number of strings in the given text.
If we go with the naive approach of pattern searching, that is, by using the KMP algorithm it'll take a much longer time. And that is one of the things your interviewer wouldn't like! So, instead of searching for each pattern one by one, we do a little bit of complex programming by building an automaton of all the given words.
Since this algorithm helps to minimize the time taken during pattern-matching, it is also a sort of Dictionary-matching Algorithm. This algorithm works in 3 phases:
- Go-To
- Failure
- Output

Don't worry as in this article, we'll understand all about these phases and how this algorithm ultimately finds the solution in complex pattern-matching problems. This algorithm basically uses the tree structure, and later, converts the tree as an automaton to implement the searching in linear time.
Explaining the working with Example
In this portion, we'll make you understand how the Aho-Corasick Algorithm works for a particular string and gives patterns. So, let's get started.
01) Preprocessing: This step happens before any of the given stages of the algorithm and is very important for the smooth functioning of this pattern-matching algorithm.
First, Build a trie of all words given which are to be found in the given string.
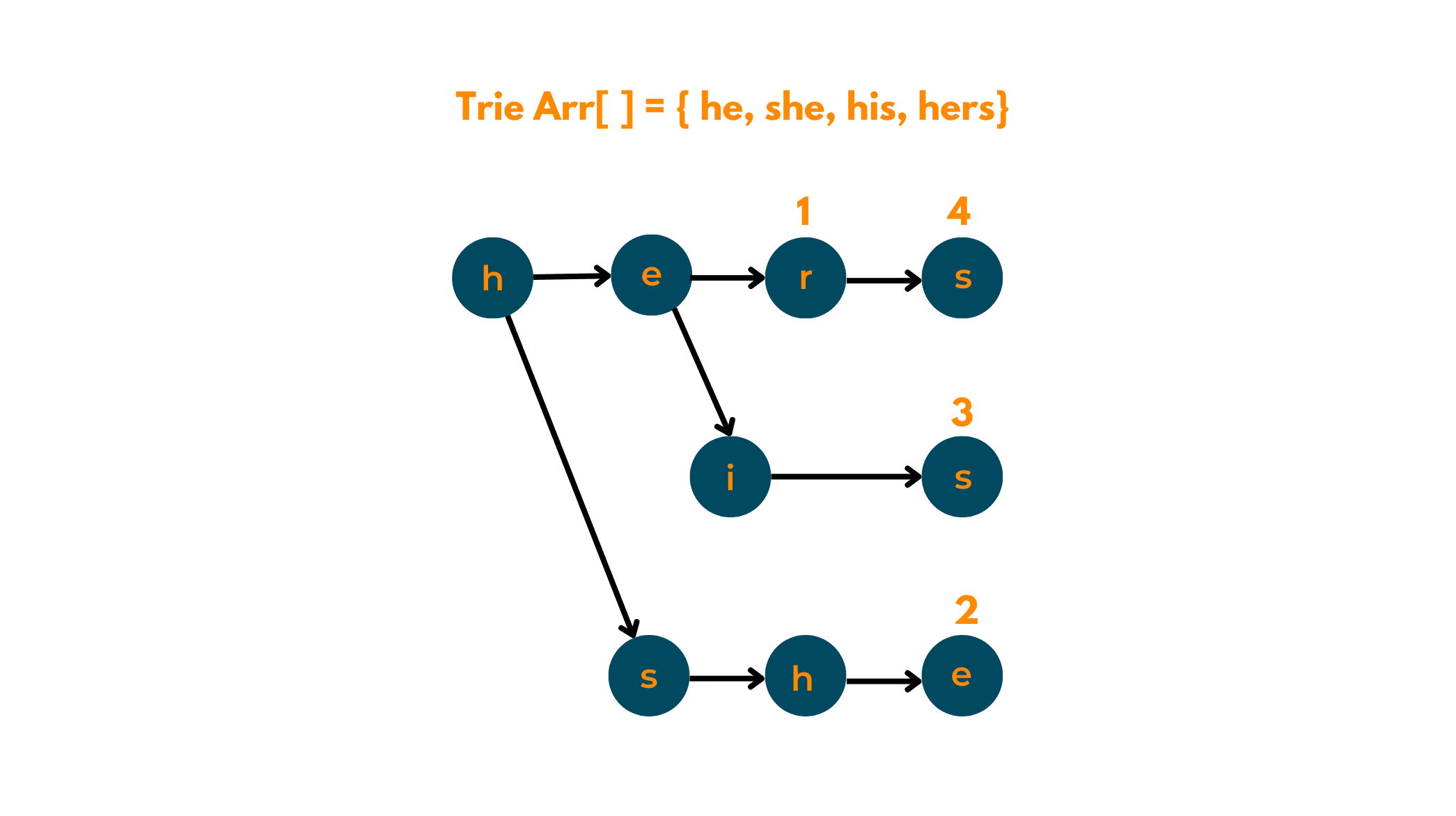
Second, extend the trie into an automaton so that time complexity can be reduced to linear.
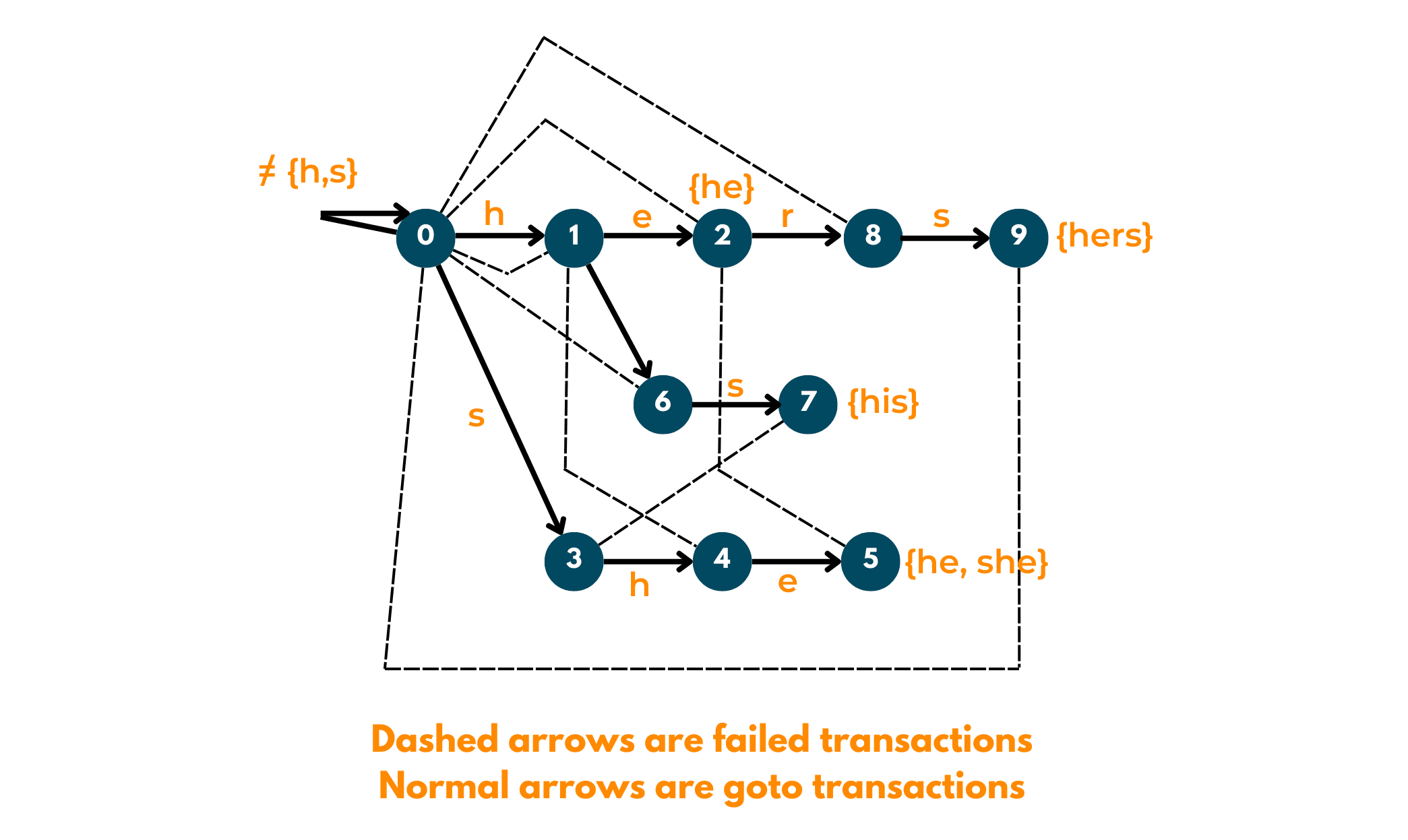
02) Go-To: After building the tree, now we move on to the first phase of pattern-matching. We observe all the characters present in the trie, and if there is any character that does not have an edge at root, we add an edge back to its root.
03) Failure: For each state, using the Breadth First Traversal, we try to find the longest proper suffix of the given string.
Output: For a particular state, indices of all words are stored in a bitwise map, to ease the retrieval process.
C++ Implementation
Here is the source code for implementing this aho-corasick algorithm in C++ languages:
using namespace std; #include <bits/stdc++.h> const int MAXS = 500; //number of states in the machine //number of characters in the english alphabet const int MAXC = 26;
//Output function is executed via out[] int out[MAXS]; //Failure function is executed via f[] int f[MAXS]; //Goto function is executed via g[][] int g[MAXS][MAXC]; int buildMatchingMachine(string arr[], int k) { //initializing the values in out function as 0. memset(out, 0, sizeof out); // Initializing the values in goto function as -1. memset(g, -1, sizeof g); int states = 1;
// building trie for arr[] for (int i = 0; i < k; ++i) { const string &word = arr[i]; int currentState = 0; // Inserting all characters for (int j = 0; j < word.size(); ++j) { int ch = word[j] - 'a'; if (g[currentState][ch] == -1) g[currentState][ch] = states++; currentState = g[currentState][ch]; }
//adding current word in output function out[currentState] |= (1 << i); } for (int ch = 0; ch < MAXC; ++ch) if (g[0][ch] == -1) g[0][ch] = 0; //building failure function and inserting values in fail function memset(f, -1, sizeof f); queue<int> q; for (int ch = 0; ch < MAXC; ++ch) { if (g[0][ch] != 0) { f[g[0][ch]] = 0; q.push(g[0][ch]); } } // Now queue has states 1 and 3 while (q.size()) { // Removing front state from queue int state = q.front(); q.pop(); for (int ch = 0; ch <= MAXC; ++ch) { if (g[state][ch] != -1) { // Find failure state of removed state int failure = f[state]; while (g[failure][ch] == -1) failure = f[failure]; failure = g[failure][ch]; f[g[state][ch]] = failure; // Merge output values out[g[state][ch]] |= out[failure]; q.push(g[state][ch]); } } } return states; } int findNextState(int currentState, char nextInput) { int answer = currentState; int ch = nextInput - 'a';
while (g[answer][ch] == -1) answer = f[answer]; return g[answer][ch]; } //the below function finds all occurences of given text void searchWords(string arr[], int k, string text) { buildMatchingMachine(arr, k); int currentState = 0; for (int i = 0; i < text.size(); ++i) { currentState = findNextState(currentState, text[i]); //if match is not found, move to next state if (out[currentState] == 0) continue; // if match is found, print the occurences for (int j = 0; j < k; ++j) { if (out[currentState] & (1 << j)) { cout << "Word " << arr[j] << " appears from " << i - arr[j].size() + 1 << " to " << i << endl; } } } } int main() { string arr[] = {"he", "she", "hers", "his"}; string text = "ahishers"; int k = sizeof(arr)/sizeof(arr[0]); searchWords(arr, k, text); return 0; }
Java Implementation
Here is the source code for implementing this aho-corasick algorithm in Java languages:
import java.util.*; class Solution{ // maximum number os states in the machine = sum of length of all keywords static int MAXS = 500; // maximum number of characters = 26 static int MAXC = 26; // function to print is implemented using out[] static int []out = new int[MAXS]; //function to show failure is implmeneted using f[] static int []f = new int[MAXS];
static int [][]g = new int[MAXS][MAXC]; static int buildMatchingMachine(String arr[], int k) { //initializing all array values as 0 Arrays.fill(out, 0); //initializing all values in goto function as -1 for(int i = 0; i < MAXS; i++) Arrays.fill(g[i], -1); int states = 1; //Building trie for arr[] for(int i = 0; i < k; ++i) { String word = arr[i]; int currentState = 0; for(int j = 0; j < word.length(); ++j) { int ch = word.charAt(j) - 'a'; if (g[currentState][ch] == -1) g[currentState][ch] = states++; currentState = g[currentState][ch]; } //add current word out[currentState] |= (1 << i); } for(int ch = 0; ch < MAXC; ++ch) if (g[0][ch] == -1) g[0][ch] = 0; // building the failure function Arrays.fill(f, -1); Queue q = new LinkedList<>();
for(int ch = 0; ch < MAXC; ++ch) { if (g[0][ch] != 0) { f[g[0][ch]] = 0; q.add(g[0][ch]); } } while (!q.isEmpty()) {
int state = q.peek(); q.remove(); for(int ch = 0; ch < MAXC; ++ch) { if (g[state][ch] != -1) { int failure = f[state]; while (g[failure][ch] == -1) failure = f[failure]; failure = g[failure][ch]; f[g[state][ch]] = failure; out[g[state][ch]] |= out[failure]; q.add(g[state][ch]); } } } return states; }
static int findNextState(int currentState, char nextInput) { int answer = currentState; int ch = nextInput - 'a'; while (g[answer][ch] == -1) answer = f[answer]; return g[answer][ch]; } // this function finds the occurrences of given text
static void searchWords(String arr[], int k, String text) { buildMatchingMachine(arr, k); int currentState = 0; for(int i = 0; i < text.length(); ++i) { currentState = findNextState(currentState, text.charAt(i)); //if match not found, then move to next state if (out[currentState] == 0) continue; for(int j = 0; j < k; ++j) { if ((out[currentState] & (1 << j)) > 0) { System.out.print("Word " + arr[j] +" appears from " +(i - arr[j].length() + 1) + " to " + i + "\n"); } } } } public static void main(String[] args) { String arr[] = { "he", "she", "hers", "his" }; String text = "ahishers"; int k = arr.length; searchWords(arr, k, text); } }
Python Implementation
Here is the source code for implementing this aho-corasick algorithm in Python languages:
from collections import defaultdict class ahocorasick: def __init__(self, words): self.max_states = sum([len(word) for word in words]) self.max_characters = 26 self.out = [0]*(self.max_states+1) self.fail = [-1]*(self.max_states+1) self.goto = [[-1]*self.max_characters for _ in range(self.max_states+1)] for i in range(len(words)): words[i] = words[i].lower() self.words = words self.states_count = self.__build_matching_machine() def __build_matching_machine(self): k = len(self.words) states = 1 for i in range(k): word = self.words[i] current_state = 0 for character in word: ch = ord(character) - 97 if self.goto[current_state][ch] == -1: self.goto[current_state][ch] = states states += 1 current_state = self.goto[current_state][ch] self.out[current_state] |= (1<<i) for ch in range(self.max_characters): if self.goto[0][ch] == -1: self.goto[0][ch] = 0 queue = [] for ch in range(self.max_characters): if self.goto[0][ch] != 0: self.fail[self.goto[0][ch]] = 0 queue.append(self.goto[0][ch]) while queue: state = queue.pop(0) for ch in range(self.max_characters): if self.goto[state][ch] != -1: failure = self.fail[state] while self.goto[failure][ch] == -1: failure = self.fail[failure] failure = self.goto[failure][ch] self.fail[self.goto[state][ch]] = failure self.out[self.goto[state][ch]] |= self.out[failure] queue.append(self.goto[state][ch]) return states def __find_next_state(self, current_state, next_input): answer = current_state ch = ord(next_input) - 97 while self.goto[answer][ch] == -1: answer = self.fail[answer] return self.goto[answer][ch] def search_words(self, text): text = text.lower() current_state = 0 result = defaultdict(list) for i in range(len(text)): current_state = self.__find_next_state(current_state, text[i]) if self.out[current_state] == 0: continue for j in range(len(self.words)): if (self.out[current_state] & (1<<j)) > 0: word = self.words[j] result[word].append(i-len(word)+1) return result
if __name__ == "__main__": words = ["he", "she", "hers", "his"] text = "ahishers" aho_chorasick = AhoCorasick(words) result = aho_chorasick.search_words(text) for word in result: for i in result[word]: print("Word", word, "appears from", i, "to", i+len(word)-1)
Output:
Word 'his' appears from 1 to 3 Word 'he' appears from 4 to 5 Word 'she' appears from 3 to 5 Word 'hers' appears from 4 to 7
Applications of the Aho-Corasick Algorithm
Below we have listed a few applications of this wonderful algorithm:
- To find all strings from the given text.
- To find the lexicographically smallest string of a given length.
- To find the shortest string that contains all the given strings.
Complexity Analysis of Aho-Corasick
Time Complexity for Aho-Corasick Algorithm is O(n+l+z), where, n is the length of text, l is the length of words to be searched and z is the number of matches. Space Complexity for this algorithm is O(l*q), where q is the length of the alphabet or, the maximum number of children a node can have.
Conclusion
The Aho-Corasick algorithm is surely a complex, yet better way to cover and complete all those hard pattern-matching problems. Students tend to leave this topic, but think of how great the interviewer will think of you if you solve such a question with linear time complexity!