Rabin-Karp Algorithm for Pattern Search (C++ & Java Code)

If you are from a computer science background, you must know the importance of strings and patterns in the Data Structures & Algorithms world. Even though we have loads of data structures for information, strings are the only ones used for word processing. 

In this tech blog, we are going to learn about a crucial and very optimal string algorithm that is often the first choice for pattern-matching problems. Yes, we'll be learning about the Rabin-Karp Algorithm today!  We'll get a good understanding of what this algorithm is, a solved example using this algorithm for your ease, and last but not least its implementation in C++ and Java languages.

So, it's going to be an exciting ride, let's go!

What is Rabin-Karp Algorithm?

Patterns in a string are quite common to find with eyes, but what if you need an algorithm to search patterns in your string for a computer? Well, that's what a Rabin-Karp Algorithm is for!

A Rabin-Karp Algorithm is used for finding out patterns in a string using a Hash Function. Unlike the other alternatives present, this method does not check each and every alphabet but rather, minimizes its searching span over limited alphabets. 

Using a hash value in this algorithm is of great significance because due to this value only, the searching space is reduced manifolds and the efficiency increases tremendously. This procedure makes it much more efficient than the other methods. 

One more popular Aho-Corasick algorithm is also important for pattern searching.

Learning about the Hash Value in Rabin-Karp

What is Hash Value?

A Hash Value is a programming tool that is used for mapping a larger input to a relatively smaller output. In this world run by technology, there is information everywhere. But, how do we identify the information of what we need more than anything else?

For this, Hash Values are used. They help in uniquely identifying the information. Because of its collision resistance nature, there is a very rare chance of different information having the same hash value. 

How is Hash Value calculated in Rabin-Karp?

In the Rabin-Karp algorithm, the value of a long string is printed out as a small integer value using a hash value. If you're a curious computer geek like me and use Java as your main programming language, you must have used a function called HashCode(). If we pass a string inside this function, then on printing it we get an integer value, which is the Hash Value of the inputted string. 

But, in the Rabin-Karp algorithm, we use a special formula to find out the hash value of the pattern to be searched and compare it with the hash values of the given string to match the best. Take a look at the below formula that we use for calculating the same:

where, v = numerical value of the text in lexicographical order, eg. a=1, b=2, c=3...

          d = number of characters in the input set,

          m = length of the input set

Example: Finding the Hash Value of abc:

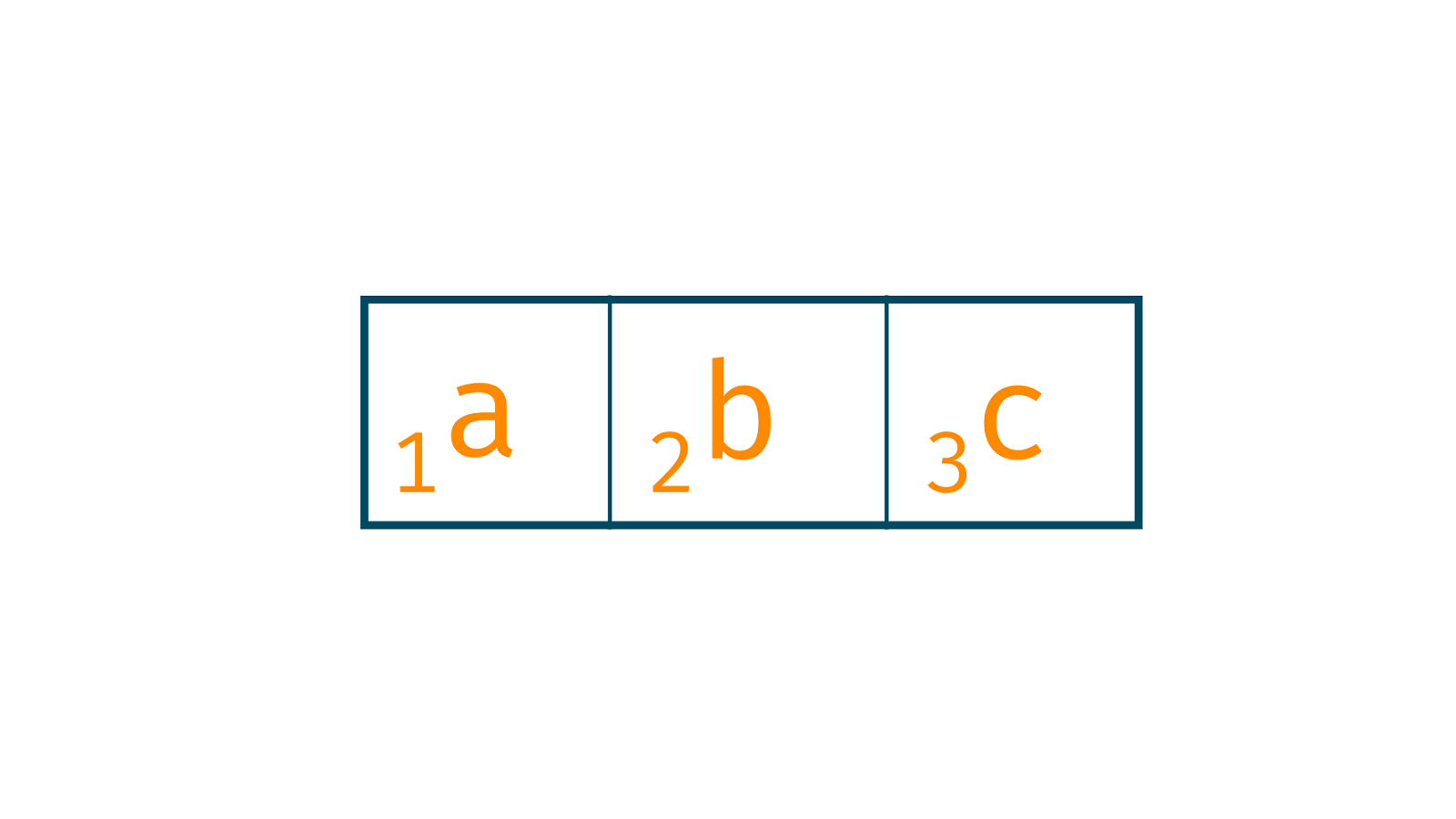
= Σ(v * dn-1) mod 13

= ((1 * 102) + (2 * 101) + (3 * 100)) mod 13

= 123 mod 13

= 6

NOTE: In the above calculations, you can take the modulus of any prime number that eases the calculation. 

Understanding working with an Example

After learning about the hash value and its significance in the Rabin-Karp algorithm, let's finally move over to how this algorithm works internally. For your ease, we have provided an example and explained the work. Let's dive in!

Given Text: ABCCDDAEFG

Text to be Searched: CDD

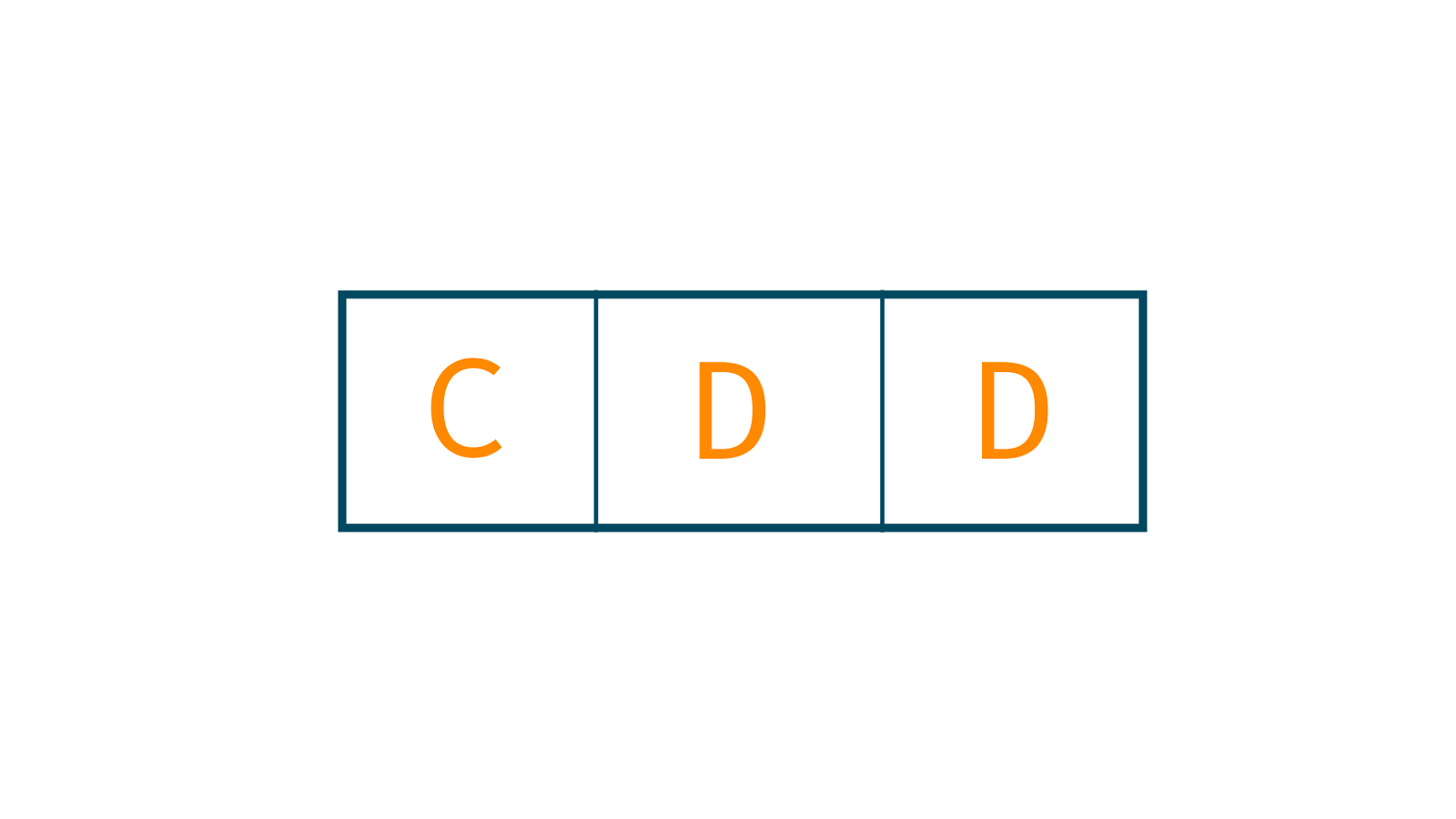
Steps to follow:

1. Assigning the Numerical Weight/ Value to the characters in general: In this step, we assign the values to the alphabets as per their lexicographical order. For eg. a=1, b=2, c=3...

2. Calculate the Hash Value of the string to be searched: Now, we calculate the hash value of the string that is to be searched with the formula that was given above, ie CDD.

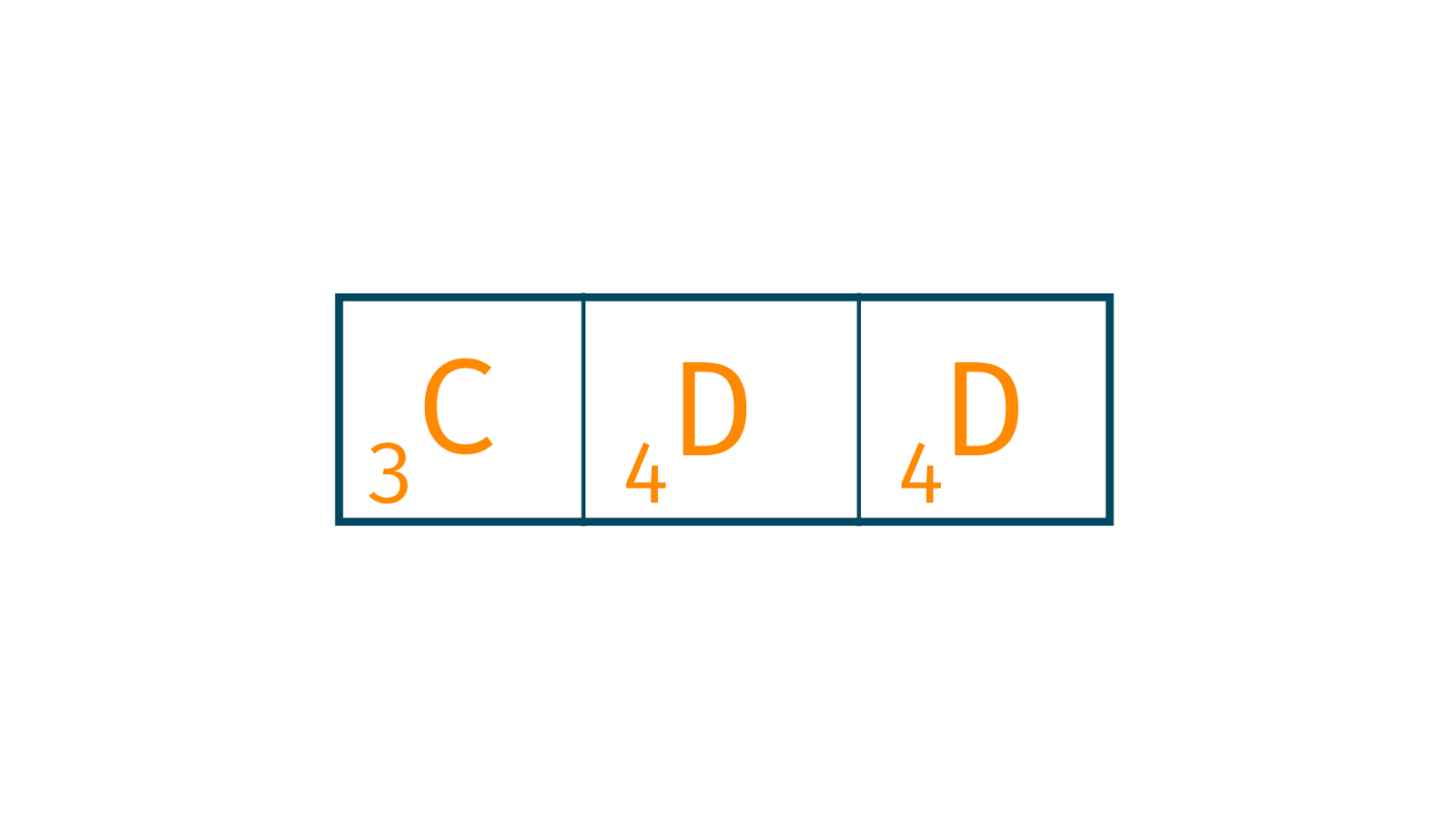
= Σ(v * dm-1) mod 13

= ((3 * 102) + (4 * 101) + (4 * 100)) mod 13

= 344 mod 13

= 6

3. Calculate the Hash Value for the text by dividing them into groups of size 'm': For the first window ABC, hash value:

= Σ(v * dn-1) mod 13

= ((1 * 102) + (2 * 101) + (3 * 100)) mod 13

= 123 mod 13

= 6

In this step, after calculating the hash value of each window one by one, we check whether the hash value of the string matches the one to be found. Look at the image below to understand:

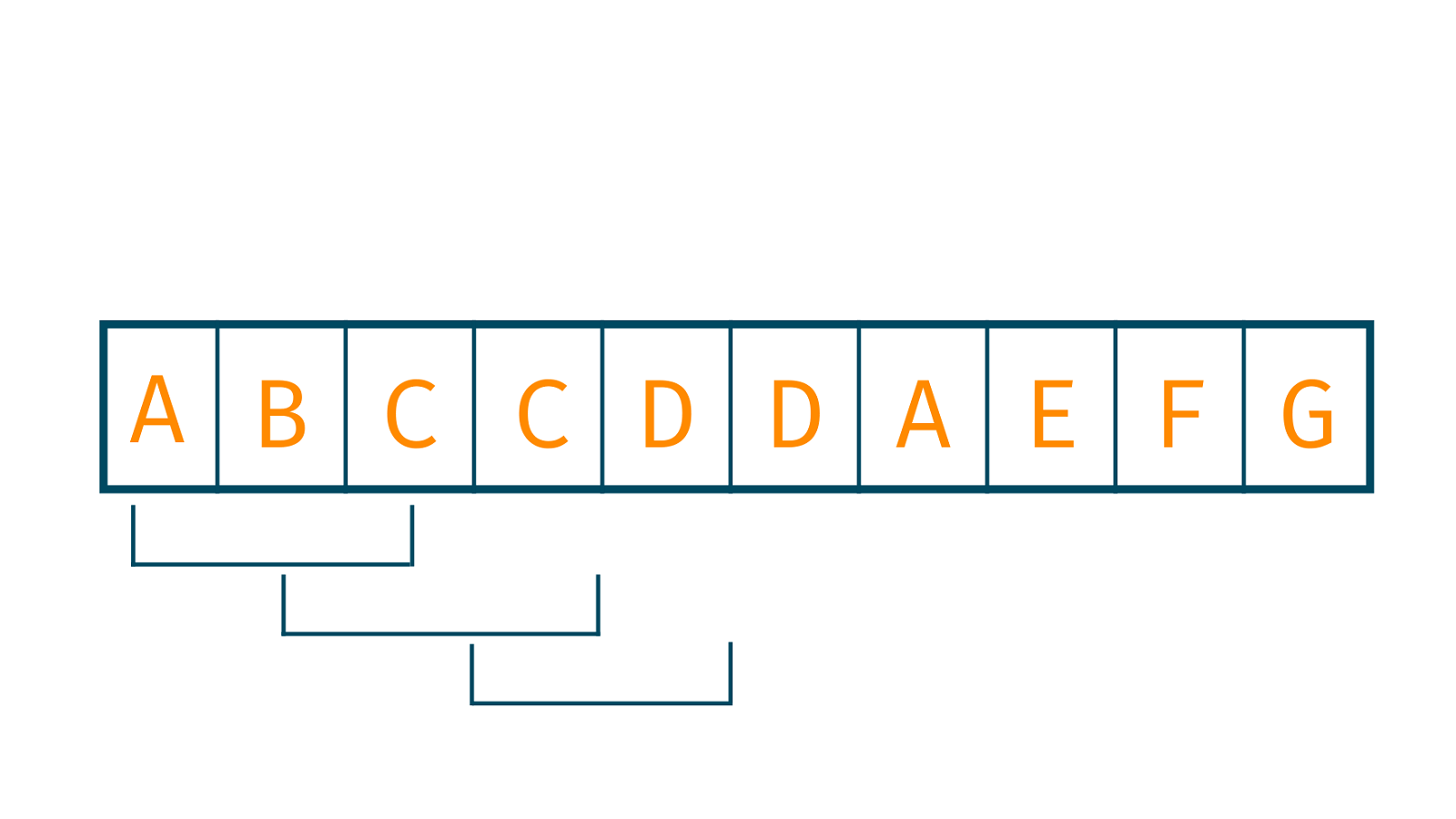
4. Comparison: You need to keep iterating and comparing the hash value of other windows and match it with the string. If it does, we perform the pattern matching for the rest of the alphabets, otherwise, we move to others. 

Output: 

True, the string contains the given text at position 2.

Implementation of Rabin-Karp with C++

#include 
#include 
using namespace std;

#define d 10

void RabinKarp(char text[], char string[], int q) {
  int m = strlen(text);
  int n = strlen(string);
  int i, j;
  int p = 0;
  int t = 0;
  int h = 1;

  for (i = 0; i < m - 1; i++)
    h = (h * d) % q;

  //hash value for string and pattern
  for (i = 0; i < m; i++) {
    p = (d * p + string[i]) % q;
    t = (d * t + pattern[i]) % q;
  }

  // Find the match
  for (i = 0; i <= n - m; i++) {
    if (p == t) {
      for (j = 0; j < m; j++) {
        if (string[i + j] != text[j])
          break;
      }

      if (j == m)
        cout << "Pattern is found at position: " << i + 1 << endl;
    }

    if (i < n - m) {
      t = (d * (t - string[i] * h) + string[i + m]) % q;

      if (t < 0)
        t = (t + q);
    }
  }
}

int main() {
  char string[] = "ABCCDDAEFG";
  char text[] = "CDD";
  int q = 13;
  RabinKarp(string, pattern, q);
}

Implementation of Rabin-Karp with Java

public class RabinKarp {
  public final static int d = 10;
  static void search(String pattern, String str, int q) {
    int m = pattern.length();
    int n = str.length();
    int i, j;
    int p = 0;
    int t = 0;
    int h = 1;

    for (i = 0; i < m - 1; i++)
      h = (h * d) % q;
    // Calculate hash value for pattern and text
    for (i = 0; i < m; i++) {
      p = (d * p + pattern.charAt(i)) % q;
      t = (d * t + str.charAt(i)) % q;
    }

    // Find the match
    for (i = 0; i <= n - m; i++) {
      if (p == t) {
        for (j = 0; j < m; j++) {
          if (str.charAt(i + j) != pattern.charAt(j))
            break;
        }
        if (j == m)
          System.out.println("Pattern is found at position: " + (i + 1));
      }

      if (i < n - m) {
        t = (d * (t - str.charAt(i) * h) + str.charAt(i + m)) % q;
        if (t < 0)
          t = (t + q);
      }
    }
  }
  public static void main(String[] args) {
    String str = "ABCCDDAEFG";
    String pattern = "CDD";
    int q = 13;
    search(pattern, str, q);
  }
}

The complexity of the algorithm

The complexity of the Rabin-Karp algorithm in a general scenario is quite good, which is O(m+n). However, if we talk about the worst case, it increases to O ((n-m+1) m. 

*m is the length of the pattern & n is the length of the string.

Comparison of Rabin-Karp with other alternatives

Since you have understood both the implementation and the theoretical knowledge behind this algorithm, you must have understood that it works in a much more efficient way as compared to other methods. Using this algorithm reduces our time complexity since we do only one comparison per text substring and match only when the hash values are found to be equal. 

Applications of the Rabin-Karp Algorithm

The Rabin-Karp Algorithm has a wide range of applications in the world of word processing and problems revolving around strings. Some other applications are listed below:

• For pattern matching
• For finding a particular text in a bigger string

Conclusion

Data Structures and Algorithms is one such field where the continuous practice is necessary to gain authority over the subject. Word Processing is gaining popularity in the outer world due to the data increasing at an exponential rate, thus understanding these types of algorithms will provide you an edge over others. At FavTutor, we not only provide these valuable tech blogs but offer 24*7 guidance over programming as well.