Imagine you have a full-fledged assignment due tomorrow and you have to write some important points about a given topic. Now, you have received an assignment from your friend but, you do not know where they've written the points. What's your first instinct?
You go up the search bar, enter the text you think will match the situation, and search for that word in the whole assignment. Ever wondered how this searching thing works? What is the process behind searching for that one word in a group of thousands and millions of words?
What do you actually mean by searching for a word? Well, it means that you're given a text 'a' and you have to search it among a cluster of words or strings called 'b'. So, we need to check very patiently whether the string 'a' is in 'b' at any point in time.
In this tech blog, we'll be approaching this algorithm and understanding all about it, step-by-step with great examples and lots of details. Let's go!
What is KMP Algorithm?
The KMP algorithm is an abbreviated form of the Knuth Morris Algorithm. Just like the Boyer-Moore algorithm, this algorithm is also highly useful for pattern searching. For general pattern-searching situations, this algorithm has proved to be a boon.
The basic idea behind implementing the KMP algorithm is to use the degenerating property of text and enhance the complexity of the whole program. Not just this, we have a lot more in this tech blog, so read on!
Basic Terminologies used in KMP Algorithm
To understand the terminologies used in this algorithm, we need to take a simple example:
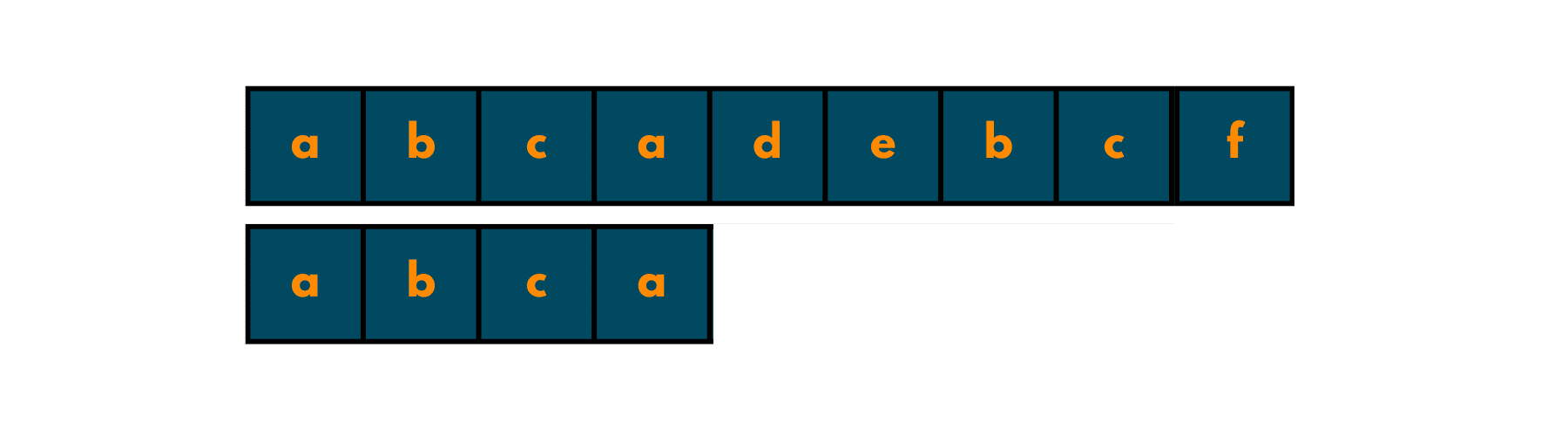
Example: {a b c d a b c}
01) Prefix
In the KMP algorithm, we have a proper prefix with which we try to find the given text. A prefix of a given string is a subset of the whole text using only some of the initial indices of the text. There's no particular limit as to how many characters you can take to make the prefix.
But, one condition you need to fulfill is that you should not take all the elements of the text. If you take all the characters of the text, then it won't be a prefix. It'll just be the whole text repeated twice.
Below are some of the prefixes that you can build for the above example:
- a
- ab
- abc
- abcd
- abcda
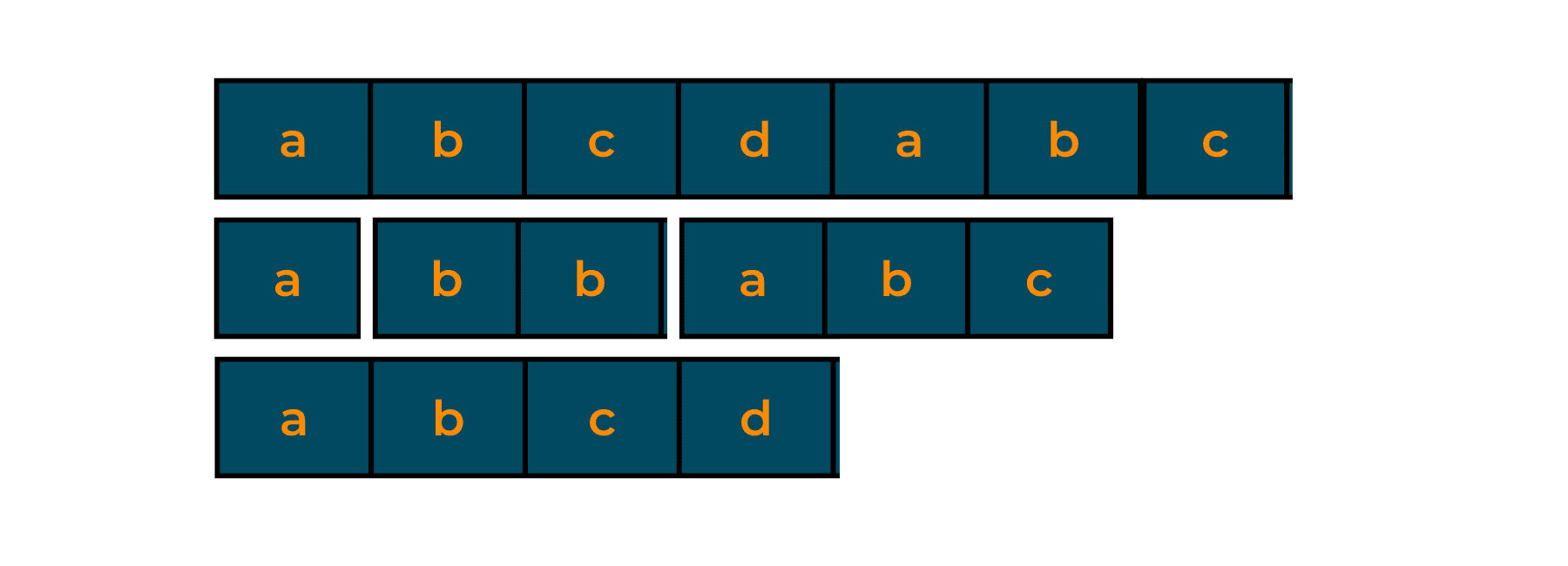
02) Suffix
A proper suffix of the given text is the word whose character is taken from the right of the text. Unlike the prefix part, it should be started from the end character of the text. Just like a prefix didn't have the last character of the text, in a suffix, you cannot have the first character of the text. '
Below are some of the suffixes, that you can make for the above example:
- c
- bc
- abc
- abcd
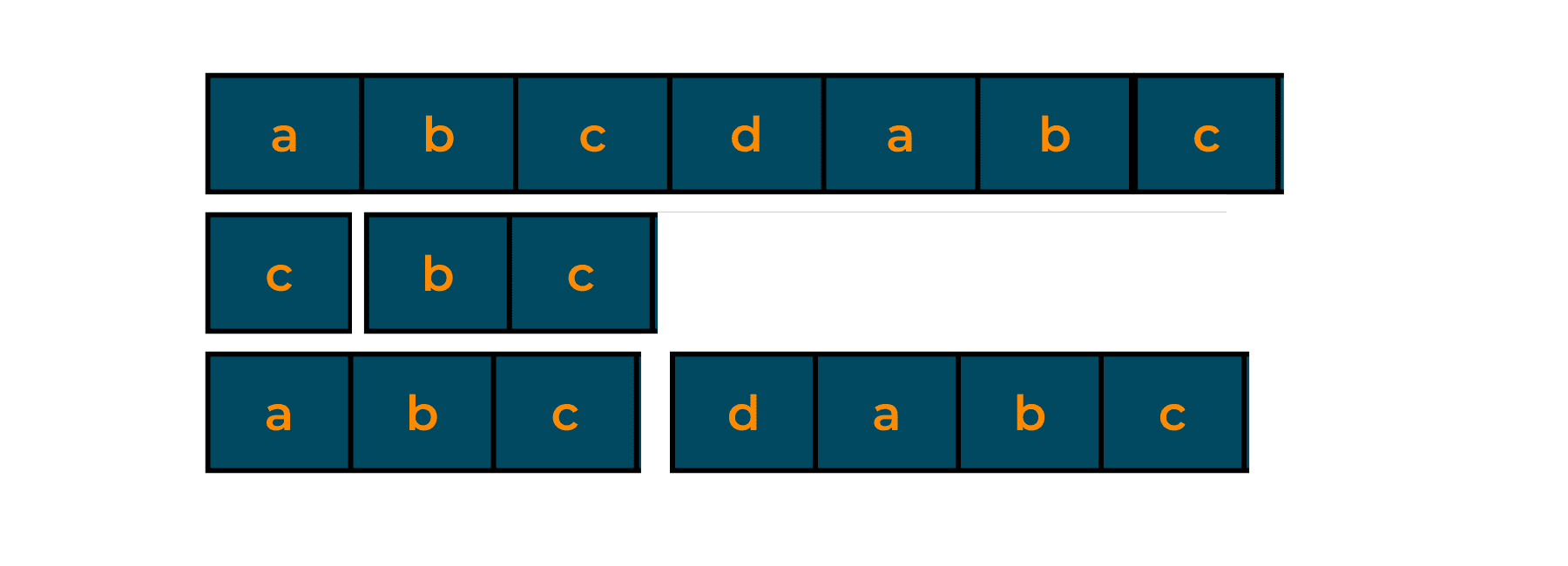
One thing to note is that a proper suffix of a given text can be the same as its proper prefix. In the given example, abc is both a prefix and a suffix.
How does Pattern Searching work in KMP Algorithm?
Now that you have understood the terminologies and the basic application of the KMP Algorithm, you are ready to have some more fun! In this section, we'll tell you about how pattern searching takes place while implementing KMP and what's the role of the LPS Table in this thing.
What is LPS Table?
LPS stands for the Longest proper prefix which is also a Suffix. To find this thing, we create an LPS table and find it. In this table, we map every character to a value. The value which is mapped to each character of the string is the length of the longest proper prefix that is also a suffix in the first given number of characters.
Let us create an LPS Table for the same example that we used earlier:
Example: {a b c d a b e}
Now, we'll start preparing the LPS Table for the above-given pattern. As mentioned above, LPS refers to the length of the longest proper prefix that is also a suffix. So, let's get started!
We'll start with the leftmost character 'a'. Now, 'a' again appears at index 4. But, we need the longest proper prefix. So, we'll now check for the next alphabet i.e., 'b'. So, we'll give them a number 1 and 2 respectively. But, even if we move forward we won't be able to find any further prefixes so, let's give all others a number 0.
The LPS Table should look like this:
| a | b | c | d | a | b | e | a | b | f |
| 0 | 0 | 0 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
Now, what we did above is not the algorithm to search pattern, but is just the basis for what lies ahead in this problem.
Try to make the LPS Table for the given patterns, so that you get some confidence.
Pattern 1: a a b c a d a a b e
Pattern 2: a b c d e a b f a b c
What to do with the LPS Table?
We created the LPS Table so that we can get rid of the partial matches that were observed in the table. If we keep on computing them, unnecessary time and memory space will be used up, slowing the process. So, in this section, we'll actually see how we compute the matching of strings with patterns.
String(in which we search the pattern): a b a b c a b c a b a b a b d
Pattern(which is to be searched): a b a b d
Take a look at the given image for seeing the pattern in the string visually:
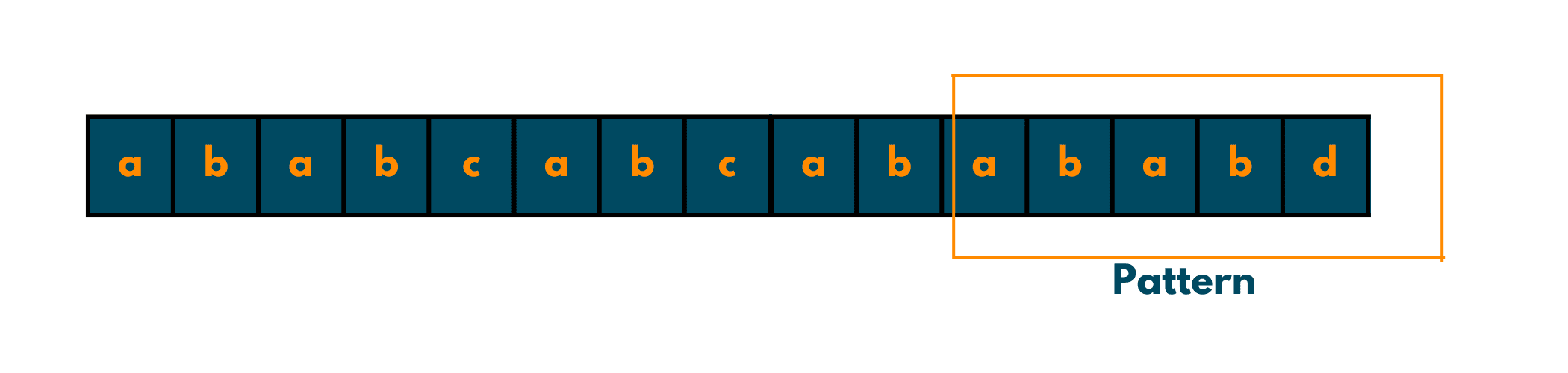
Now, we'll start with the process.
Now, we create two pointers i and j, such that, i = 0 which iterates over the string, and j = 0, which will move over the LPS table. At every stage, we compare string[i] and pattern[j].
How will iterators move? Follow the points:
- If there is a match, increment both i and j.
- If there is a mismatch after a match, place j at LPS[pattern[j - 1]] and compare again.
- If j = 0, and there is a mismatch, increment i.
Now keep these points in mind, and trace the path for the given example.
| i=0, j=0 | match |
| i = 1, j = 1 | match |
| i = 2, j = 2 | match |
| i = 3, j = 3 | match |
| i = 4, j = 4 | mismatch! |
Now, we encounter a mismatch, but instead of backtracking and spending time again and again over the same thing, we place the j pointer at LPS[j-1] and then compare the pattern[j] with string[i].
After doing it, again and again, we finally reach the index i=12 and j=4. We use the LPS table and move the j pointer to LPS[j - 1] = LPS[4 - 1] = 2 and compare it with string[12]. Here's the table:
| i=12, j=2 | match |
| i = 13, j = 3 | match |
| i = 14, j = 4 | full match! |
So, this is why we used the LPS table for matching the string with the pattern.
Code Implementation in C++
Here is the C++ code for implementing KMP Algorithm:
#include <bits/stdc++.h> void LPSArray(char* pattern, int M, int* lps); void KMPSearch(char* pattern, char* txt) { int M = strlen(pattern); int N = strlen(txt); int lps[M]; LPSArray(pattern, M, lps); int i = 0; int j = 0; while ((N - i) >= (M - j)) { if (pattern[j] == txt[i]) { j++; i++; } if (j == M) { printf("Found pattern at index %d ", i - j); j = lps[j - 1]; } else if (i < N && pattern[j] != txt[i]) { if (j != 0) j = lps[j - 1]; else i = i + 1; } } } void LPSArray(char* pattern, int M, int* lps) { int len = 0; lps[0] = 0; int i = 1; while (i < M) { if (pattern[i] == pattern[len]) { len++; lps[i] = len; i++; } else { if (len != 0) { len = lps[len - 1]; } else { lps[i] = 0; i++; } } } } int main() { char txt[] = "ABCDABABCABAB"; char pattern[] = "ABABCABAB"; KMPSearch(pattern, txt); return 0; }
Code Implementation in Java
Here is the Java code for implementing KMP Algorithm:
class Solution { void KMP(String pattern, String txt) { int M = pattern.length(); int N = txt.length(); int lps[] = new int[M]; int j = 0; LPSArray(pattern, M, lps); int i = 0; while ((N - i) >= (M - j)) { if (pattern.charAt(j) == txt.charAt(i)) { j++; i++; } if (j == M) { System.out.println("Found pattern " + "at index " + (i - j)); j = lps[j - 1]; } else if (i < N && pattern.charAt(j) != txt.charAt(i)) { if (j != 0) j = lps[j - 1]; else i = i + 1; } } } void LPSArray(String pattern, int M, int lps[]) { int len = 0; int i = 1; lps[0] = 0; while (i < M) { if (pattern.charAt(i) == pattern.charAt(len)) { len++; lps[i] = len; i++; } else { if (len != 0) { len = lps[len - 1]; } else { lps[i] = len; i++; } } } } public static void main(String args[]) { String txt = "ABABDABACDABABCABAB"; String pattern = "ABABCABAB"; new KMP_String_Matching().KMP(pattern, txt); } }
Applications of the KMP Algorithm
- KMP is used for checking plagiarism in text and web documents.
- DNA Sequencing and Bioinformatics
- Digital Forensics
- Spelling Checkers
- Spam Filters
Conclusion
So, in this tech blog, we learned about how to use the LPS table and what the use it in the KMP Algorithm. We hope you had fun while learning it and don't forget to practice the example we provided. For more such tech blogs and complex topics, you can always come to FavTutor's blogs and get the best possible understanding.








