Data Structures and Algorithms are an integral part of today's software and programming world. Every student wants to excel in this field to get a good placement in big companies. Data Structures include not just arrays, graphs, queues, and linked lists but tries as well. In today's blog, we'll be talking about Suffix Trees, their generalization, and creating them using Ukkonen's algorithm with Python, C++ & Java codes. So, let's get started.
What are Suffix Trees?
You must be aware of strings. Well, Suffix Trees are a popular tool for analyzing these text strings. A Suffix Tree contains all the suffixes of the given text. It can be known as a digital tree that provides the string's structure and uses certain algorithmic methods to find its subsets. These trees are used to solve a wide number of questions such as longest palindrome, pattern matching, and finding distinct substrings in a given string.
What are Generalized Suffix Trees?
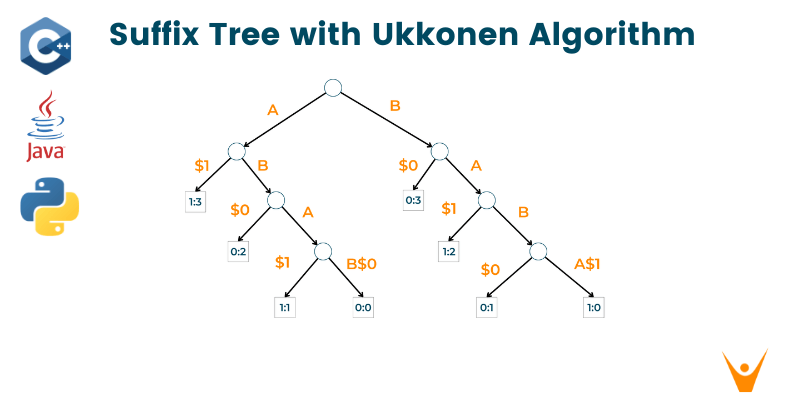
When we work with suffix trees due to their limitation, we're able to work only with the suffixes of a single string. Moving towards reality, we have to deal with several strings and suffixes at a particular time. How do we sort out this dilemma? Here's when the Generalized Suffix Trees come into the picture! As its name, these trees refer to a more generalized form of already existing suffix trees.
If there are certain strings like S1, S2, S3,...Sk, then the generalized suffix tree of all these strings will have its leaf node in a format different from others. The node labels are in the form of i:j, where, i mean the position of the string and j refers to the string whose suffix the given string is. You can also take a look at the below illustration to gain a better understanding of the concept:
Are Suffix Trees the same as Tries?
Many people confuse Suffix Trees and Tries to be the same, however, that is not true. We have given a very good illustration below to understand how these two are different, take a look!
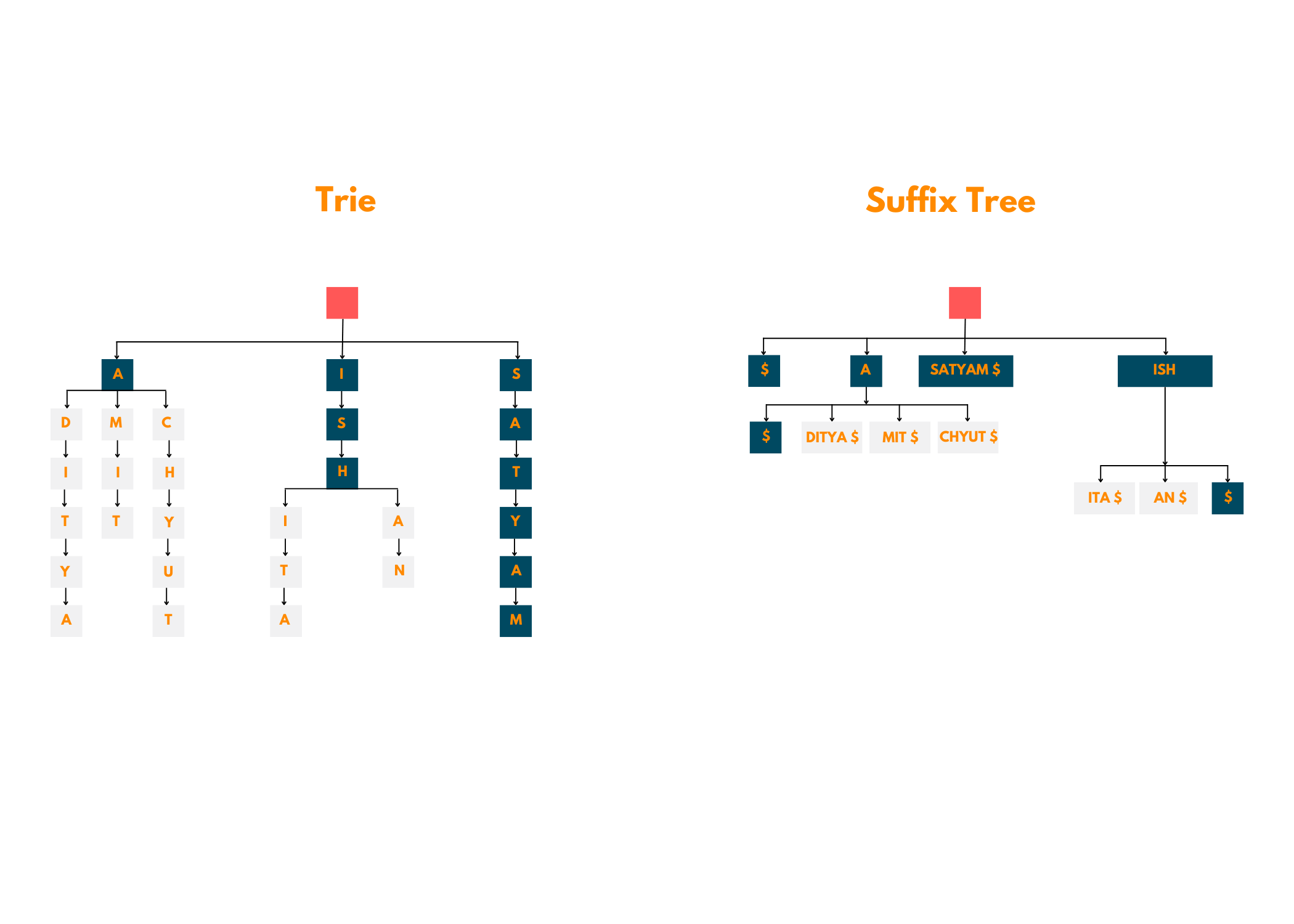
After viewing the above image, you must know that these two are not the same and should not be treated likewise. A suffix tree is essentially a compressed version of the trie and a much more efficient one too!
Understanding Ukkonen's Algorithm
In 1995, Esko Ukkonen proposed a linear time algorithm for creating suffix trees i.e., Ukkonen's Algorithm. Initially, an implicit suffix tree is created that contains the first character of the string. Then, as you move forward, it keeps on adding the other characters till the tree is complete. The orderly addition of characters in the tree maintains the on-line property of this algorithm.
*Implicit Trees are those intermediate trees that we encounter while creating the suffix tree of a given string using Ukkonen's Algorithm.
We understand that the working example of such a complex algorithm could prove to be a very important step for your learning. But, first read the below 2 statements to understand the basics.
- If you are aware of tries, it's going to be really for you. We are essentially building a similar thing so, eventually, you're going to come across root edges, edges coming out to lead to newer edges and, so on.
- But, as we have mentioned in the above section, the edge labels are not single characters. So, while working you have to keep this in mind.
Creating Suffix Tree using Ukkonen's Algorithm
We'll begin by learning the easy string suffix trees using this algorithm. Here, we'll use a very simple string that has no special characters: abc. Follow the steps below to create its suffix tree:
- The algorithm works for the strings in left to right order. For each character of the string, we move ahead by one step.
- So, beginning from left to right, we first encounter a. So, we create an edge from the root node to a leaf by labeling it as [0,#]. Here, # means the current end. Now, this edge that we just created represents the substring starting at 0 and ending at the current end, 1.
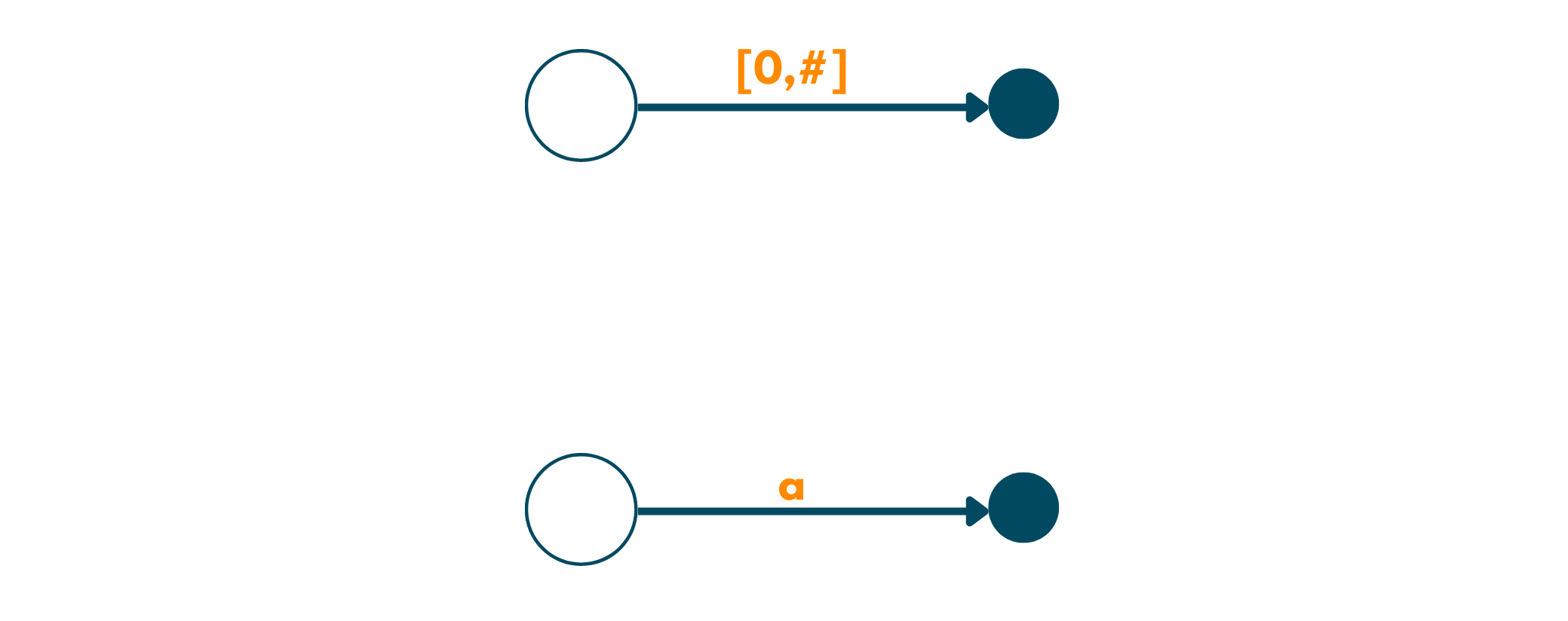
3. Moving over to the second position, we expand the current edge of a to ab labeling it as [0,#]. But, since b is also a suffix, we add another edge for it, [1,#]. We did this modification because we are now at position 1 of the string(indexing begins with 0) and ends till the current end.
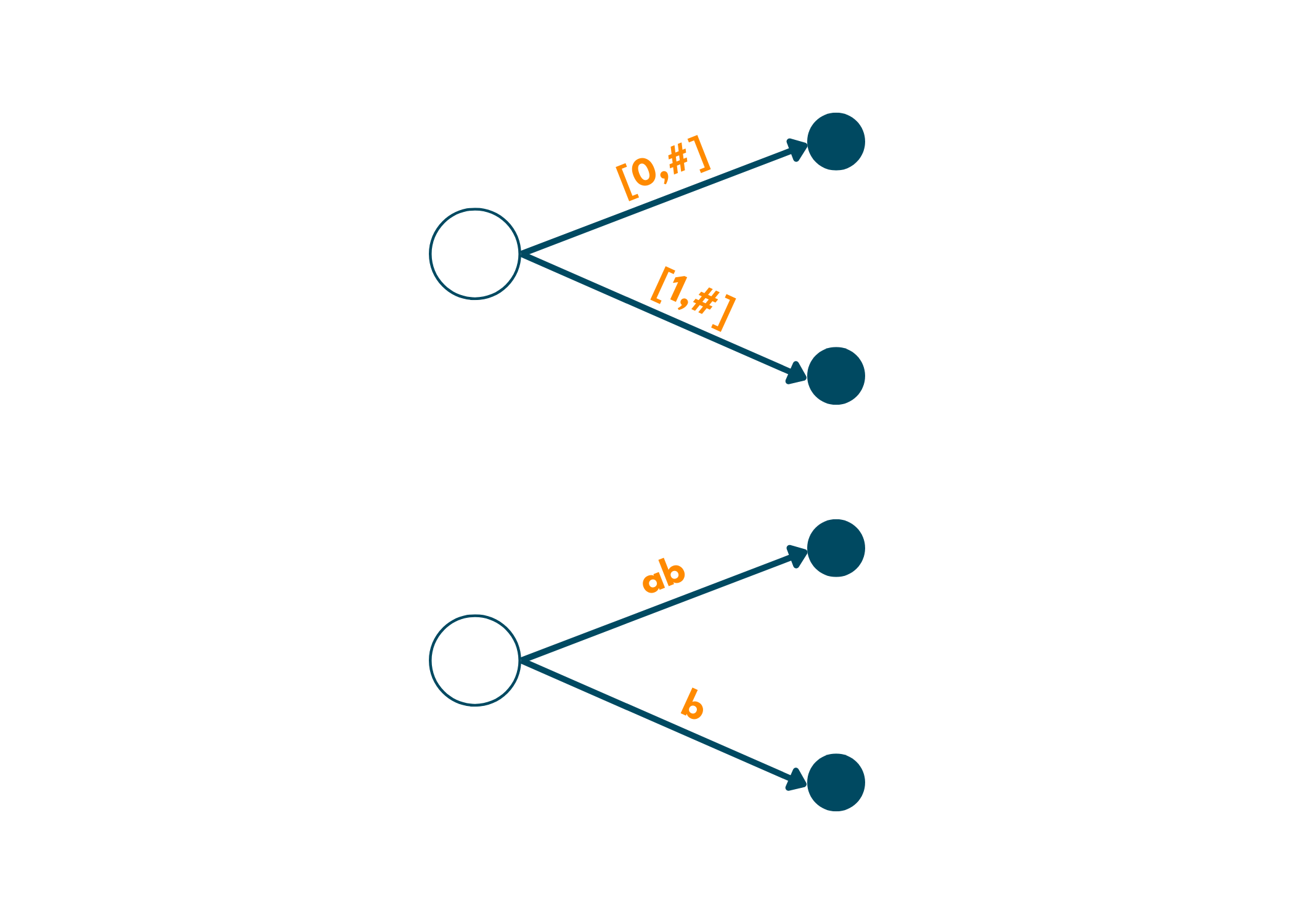
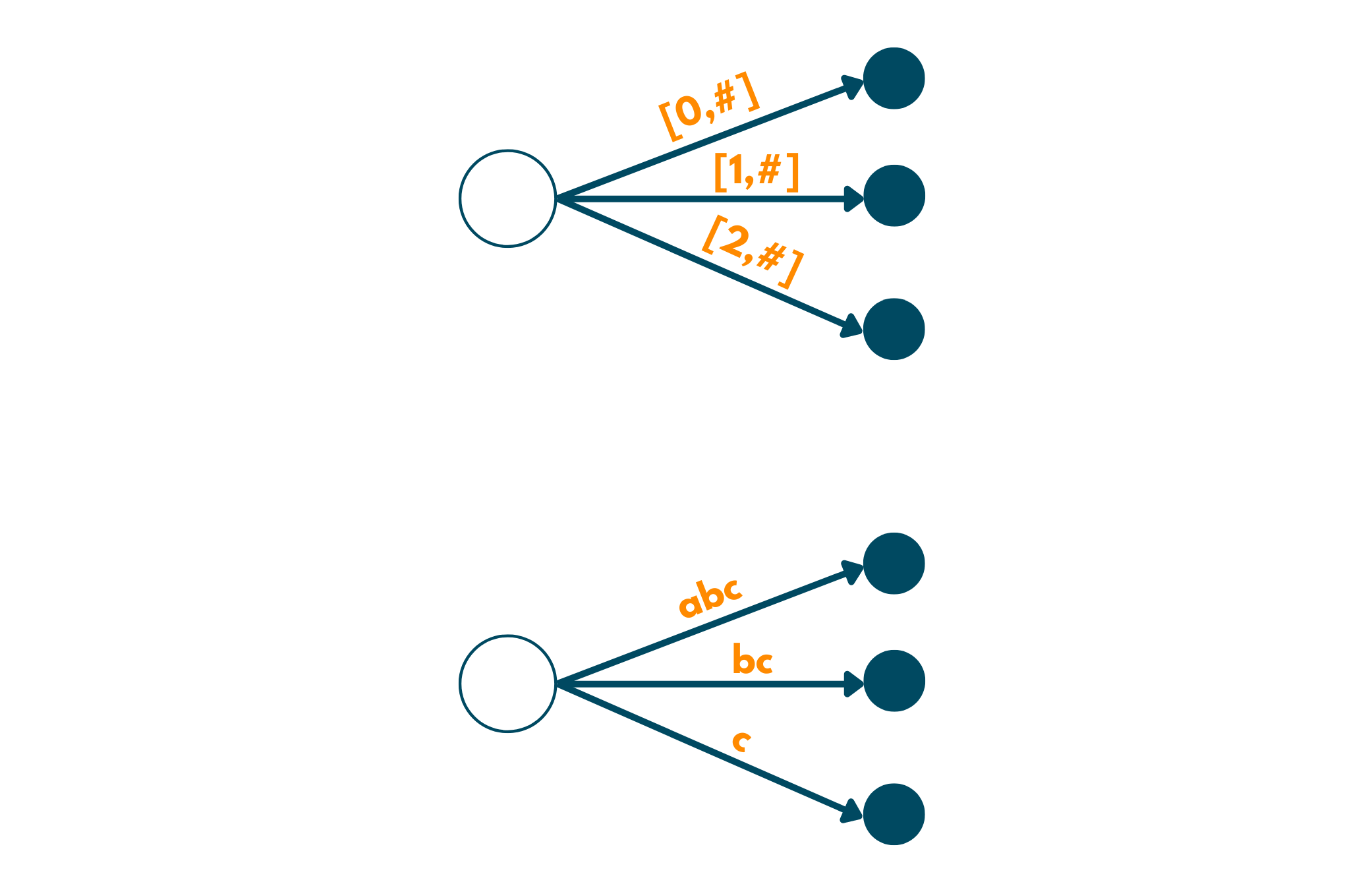
4. We again move forward and encounter c. Now, we again have to update and create a new edge as c is also a suffix of the given string. Look down below for what the tree will look like, now.
Pseudocode of Ukkonen's Algorithm
function insert(T, string, start_index, length){ i = start_index while(i < length) if T.arr[string[i]]) is NULL T.arr[string[i]] = new node() T = T.arr[string[i]] while(i < length) T.label = T.label+string[i] i = i+1 endwhile return endif j=0, x=i temp = T.arr[string[i]] while j < temp.label.length and i < length && temp.label[j] = string[i] i = i+1 j = j+1 endwhile if i = length return endif if j = temp.label.length cnt = 0 for k = 'a' to 'z' if temp.arr[k] = NULL cnt = cnt+1 endif endfor if cnt = 27 while i < length temp.label = temp.label + string[i] i = i+1 endwhile else T = temp endifelse else newInternalNode = new node() k=0 while k < j newInternalNode.label = newInternalNode.label + temp.label[k] k = k+1 endwhile newInternalNode.arr[string[j]] = new node() while k < temp.label.length newInternalNode.arr[string[j]].label+=temp.label[k] k = k+1 endwhile for k = 'a' to 'z' newInternalNode.arr[string[j]].arr[k] = temp.arr[k] endfor T.arr[string[x]] = newInternalNode T = T.arr[string[x]] endifelse endwhile } function makeSuffixTree(string, length){ Trie T string = concatenate(string, "{") for i = 0 to length insertInTrie(T, string, i, length) }
Implementation of Suffix Tree
While implementing suffix trees certain things need to be kept in mind. In this portion, we'll be covering every minute detail you will require to implement a suffix tree. The full suffix tree can be expressed in Theta(n) space if all its edges and nodes can be expressed in the same space.
The parent-child connections among the nodes in a tree are both essential and sensitive, so you need to consider that in great detail. Quite often, programmers use sibling lists in which each node has a pointer pointing to the next child. Other solutions include hash maps, balanced search trees, and sorted or unsorted arrays.
Below, we have given a table of certain options for implementing suffix trees and their time complexity:
| Implementation | Extraction | Insertion | Traversal |
| Hash Map | O(1) | O(1) | O(n) |
| Sorted Arrays | O(logn) | O(n) | O(1) |
| Bitwise Sibling Tree | O(logn) | O(1) | O(1) |
| Balanced Search Tree | O(logn) | O(logn) | O(1) |
| Hash Map + Sibling List | O(1) | O(1) | O(1) |
| Sibling Lists | O(n) | O(1) | O(1) |
Implementation of Suffix Tree with C++ Code
#include #include #include struct Node { std::string sub = ""; // a substring of the input string std::vector<int> ch; // vector of child nodes Node() { // empty } Node(const std::string& sub, std::initializer_list<int> children) : sub(sub) { ch.insert(ch.end(), children); } }; struct SuffixTree { std::vector<Node> nodes; SuffixTree(const std::string& str) { nodes.push_back(Node{}); for (size_t i = 0; i < str.length(); i++) { addSuffix(str.substr(i)); } } void visualize() { if (nodes.size() == 0) { std::cout << "\n"; return; } std::function<void(int, const std::string&)> f; f = [&](int n, const std::string & pre) { auto children = nodes[n].ch; if (children.size() == 0) { std::cout << "- " << nodes[n].sub << '\n'; return; } std::cout << "+ " << nodes[n].sub << '\n'; auto it = std::begin(children); if (it != std::end(children)) do { if (std::next(it) == std::end(children)) break; std::cout << pre << "+-"; f(*it, pre + "| "); it = std::next(it); } while (true); std::cout << pre << "+-"; f(children[children.size() - 1], pre + " "); }; f(0, ""); } private: void addSuffix(const std::string & suf) { int n = 0; size_t i = 0; while (i < suf.length()) { char b = suf[i]; int x2 = 0; int n2; while (true) { auto children = nodes[n].ch; if (x2 == children.size()) { // no matching child, remainder of suf becomes new node n2 = nodes.size(); nodes.push_back(Node(suf.substr(i), {})); nodes[n].ch.push_back(n2); return; } n2 = children[x2]; if (nodes[n2].sub[0] == b) { break; } x2++; } // find prefix of remaining suffix in common with child auto sub2 = nodes[n2].sub; size_t j = 0; while (j < sub2.size()) { if (suf[i + j] != sub2[j]) { // split n2 auto n3 = n2; // new node for the part in common n2 = nodes.size(); nodes.push_back(Node(sub2.substr(0, j), { n3 })); nodes[n3].sub = sub2.substr(j); // old node loses the part in common nodes[n].ch[x2] = n2; break; // continue down the tree } j++; } i += j; // advance past part in common n = n2; // continue down the tree } } }; int main() { SuffixTree("banana$").visualize(); }
Output:
+ +-- banana$ +-+ a | +-+ na | | +-- na$ | | +-- $ | +-- $ +-+ na | +-- na$ | +-- $ +-- $
Implementation with Java Code
import java.util.ArrayList; import java.util.List; public class SuffixTreeProblem { private static class Node { String sub = ""; // a substring of the input string List<Integer> ch = new ArrayList<>(); // list of child nodes } private static class SuffixTree { private List<Node> nodes = new ArrayList<>(); public SuffixTree(String str) { nodes.add(new Node()); for (int i = 0; i < str.length(); ++i) { addSuffix(str.substring(i)); } } private void addSuffix(String suf) { int n = 0; int i = 0; while (i < suf.length()) { char b = suf.charAt(i); List<Integer> children = nodes.get(n).ch; int x2 = 0; int n2; while (true) { if (x2 == children.size()) { // no matching child, remainder of suf becomes new node. n2 = nodes.size(); Node temp = new Node(); temp.sub = suf.substring(i); nodes.add(temp); children.add(n2); return; } n2 = children.get(x2); if (nodes.get(n2).sub.charAt(0) == b) break; x2++; } // find prefix of remaining suffix in common with child String sub2 = nodes.get(n2).sub; int j = 0; while (j < sub2.length()) { if (suf.charAt(i + j) != sub2.charAt(j)) { // split n2 int n3 = n2; // new node for the part in common n2 = nodes.size(); Node temp = new Node(); temp.sub = sub2.substring(0, j); temp.ch.add(n3); nodes.add(temp); nodes.get(n3).sub = sub2.substring(j); // old node loses the part in common nodes.get(n).ch.set(x2, n2); break; // continue down the tree } j++; } i += j; // advance past part in common n = n2; // continue down the tree } } public void visualize() { if (nodes.isEmpty()) { System.out.println(""); return; } visualize_f(0, ""); } private void visualize_f(int n, String pre) { List<Integer> children = nodes.get(n).ch; if (children.isEmpty()) { System.out.println("- " + nodes.get(n).sub); return; } System.out.println("? " + nodes.get(n).sub); for (int i = 0; i < children.size() - 1; i++) { Integer c = children.get(i); System.out.print(pre + "??"); visualize_f(c, pre + "? "); } System.out.print(pre + "??"); visualize_f(children.get(children.size() - 1), pre + " "); } } public static void main(String[] args) { new SuffixTree("banana$").visualize(); } }
Output:
? ??- banana$ ??? a ? ??? na ? ? ??- na$ ? ? ??- $ ? ??- $ ??? na ? ??- na$ ? ??- $ ??- $
Implementation with Python Code
class Node: def __init__(self, sub="", children=None): self.sub = sub self.ch = children or [] class SuffixTree: def __init__(self, str): self.nodes = [Node()] for i in range(len(str)): self.addSuffix(str[i:]) def addSuffix(self, suf): n = 0 i = 0 while i < len(suf): b = suf[i] x2 = 0 while True: children = self.nodes[n].ch if x2 == len(children): # no matching child, remainder of suf becomes new node n2 = len(self.nodes) self.nodes.append(Node(suf[i:], [])) self.nodes[n].ch.append(n2) return n2 = children[x2] if self.nodes[n2].sub[0] == b: break x2 = x2 + 1 # find prefix of remaining suffix in common with child sub2 = self.nodes[n2].sub j = 0 while j < len(sub2): if suf[i + j] != sub2[j]: # split n2 n3 = n2 # new node for the part in common n2 = len(self.nodes) self.nodes.append(Node(sub2[:j], [n3])) self.nodes[n3].sub = sub2[j:] # old node loses the part in common self.nodes[n].ch[x2] = n2 break # continue down the tree j = j + 1 i = i + j # advance past part in common n = n2 # continue down the tree def visualize(self): if len(self.nodes) == 0: print "" return def f(n, pre): children = self.nodes[n].ch if len(children) == 0: print "--", self.nodes[n].sub return print "+-", self.nodes[n].sub for c in children[:-1]: print pre, "+-", f(c, pre + " | ") print pre, "+-", f(children[-1], pre + " ") f(0, "") SuffixTree("banana$").visualize()
Output:
+- +- -- banana$ +- +- a | +- +- na | | +- -- na$ | | +- -- $ | +- -- $ +- +- na | +- -- na$ | +- -- $ +- -- $
Time Complexity
Generally, the implementation of Ukkonen's algorithm for creating a suffix tree of a given string takes O(n^2) or O(n^3) time complexity where n refers to the length of the string. But, if we use a few algorithmic techniques, we can reduce its time complexity to O(n).
Conclusion
Suffix trees are used to solve many problems that involve strings in fields like text editing, free text search, pattern matching, etc. Understanding this concept and working with Ukkonen's algorithm can take you one step closer to your goal of getting placed in a good organization. Therefore, keep practicing these types of concepts that we bring to you at FavTutor.