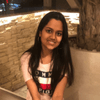Tech Companies like to hire candidates with good problem-solving capabilities. So, they come up with a variety of problems to assess their skills. One such problem is the “merge k sorted lists” problem. In this article, we will discuss how to merge K-sorted Linked Lists using the min heap and divide & conquer method. So, get ready because it is going to be an interesting ride!
What is the 'merge k sorted list' problem?
The "Merge k Sorted Lists" topic is a difficult programming challenge requiring a solid grasp of data structures and algorithms. It requires combining k-sorted linked lists into a single sorted linked list.
Here is the problem statement we are going to solve: “Given k linked lists, each linked list is sorted in ascending order. Merge all the linked lists into one sorted linked list and return it.”
Look at the illustration below to understand the problem statement better.
Several approaches exist in the programming world to solve this problem, some efficient and some not so efficient.
The first way of solving this problem is by connecting all the k-linked lists into one list. After this, use some sorting algorithm to sort the list in ascending order. That’s it! the problem is solved. However, this approach is not so efficient as it does not take advantage of the fact that each linked list is already sorted. This method has the time complexity of O(n.log(n)).
The second naïve approach to solve this problem is by making the first list the result list. Then traverse through each of the remaining lists, starting from the second list, and insert every node of the currently traversed list into the result list at its correct position, such that the resulting result list is sorted.
Merging K-Sorted Lists using Min Heap
From the above two approaches, we saw that we need a method that takes advantage of the lists being sorted and generates a new sorted list efficiently. What if we use some data structure that is specifically designed to give us the min element at each step, Does a data structure like this exists?
Well, the answer is Yes. There is a data structure called the min-heap, which will help us in solving this problem. A heap data structure that allows for fast insertion and removal of items while retaining sorted order, is one way to overcome this challenge.
The idea here is to take advantage of the fact that the root of a min-heap always gives us the smallest element. What we do in this approach is that since all the linked lists are already sorted, therefore the first elements of all of the lists will be the smallest element in their respective lists.
We take advantage of this situation by putting the first element of all the linked lists into a min-heap. We then extract the top element (root) of the min-heap to get the smallest element. By doing this we get the smallest element across all the linked lists.
After this, we increment the pointer of the list to which the recently extracted element belonged to point to the next element, and that element is now added to the min-heap. An element from the min-heap is again extracted, the pointer of the linked list which contained that element is incremented and the newly pointed element is added to the min-heap.
This process continues until the min-heap is empty. Note that we are maintaining a separate result list, to which keep adding the element which we extract from the min-heap.
Here is a simple step-by-step algorithm to implement it:
- Construct a min-heap and put the first element of each of the 'k' linked lists in it.
- Perform the following steps until the min-heap is not empty:
- Remove the root element of the min-heap and add it to the result list
- If an element (in the same linked list) exists adjacent to the element that was popped out in the previous phase, add it to the min-heap.
- Return the head node address of the result list.
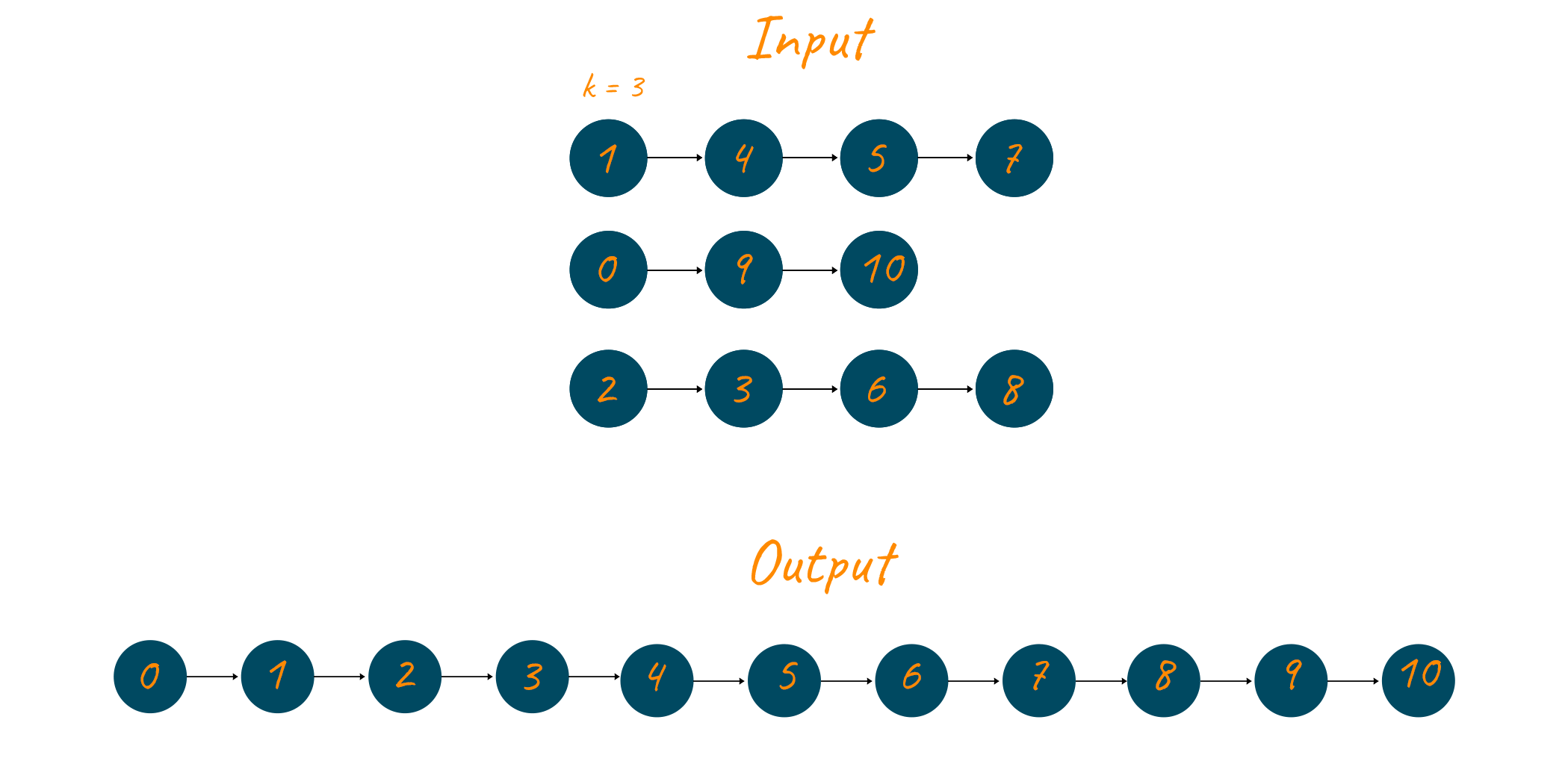
Let us take an example now to better understand the algorithm. Suppose we are given the following linked lists:
Now the min-heap is built using the first element of all the linked lists. See below

The root element (0) of this min-heap is popped. The element popped belongs to the second linked list and since it contains an element (6) next to it, therefore the pointer of the second linked list is updated to point to 6 now and 6 is inserted into the min-heap. The element extracted at this step, which is 0, is inserted into the result list.
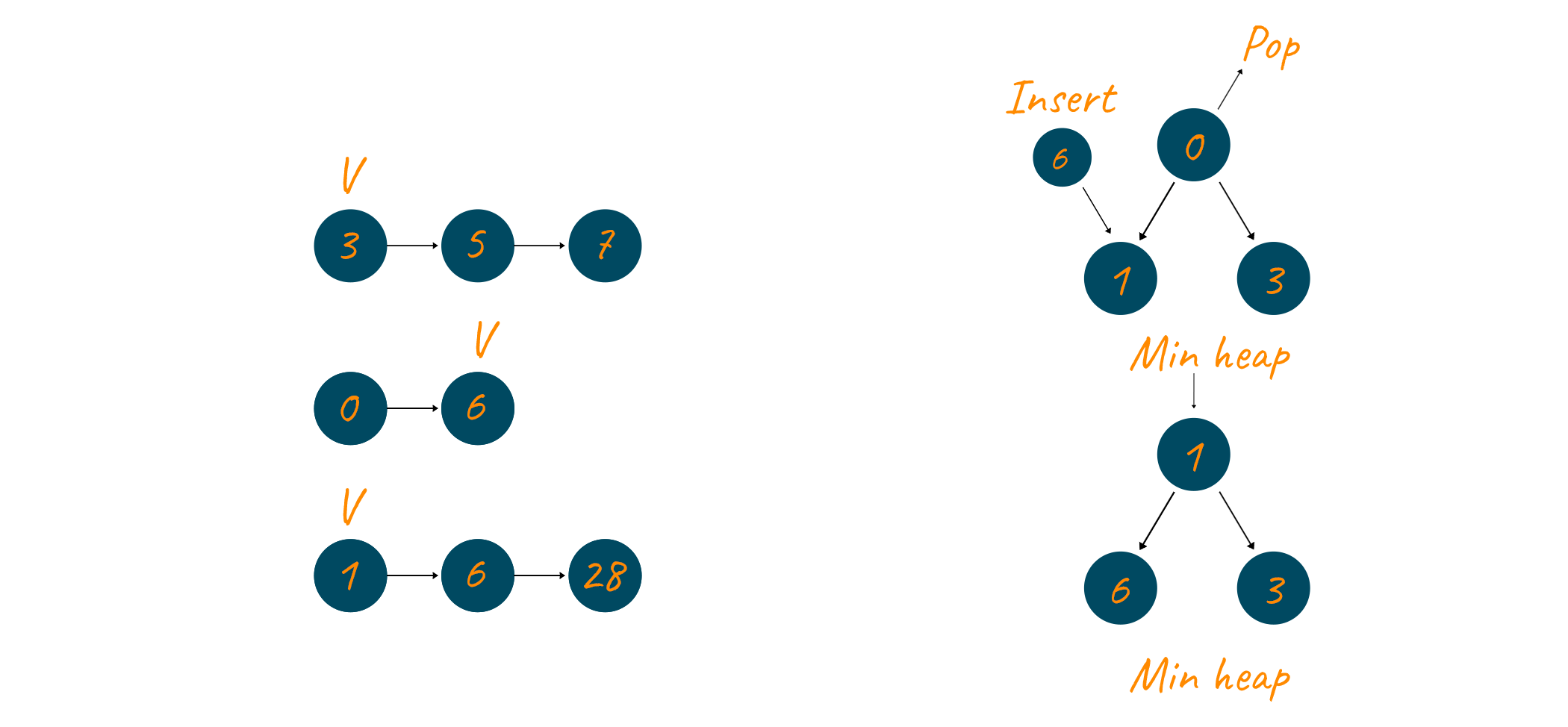
The root element i.e., 1 is again popped and added to the result linked list. Since 1 belonged to the third linked list/, therefore, the pointer of this linked list is updated to point to the next element, which is 6 and it is added to the min-heap.
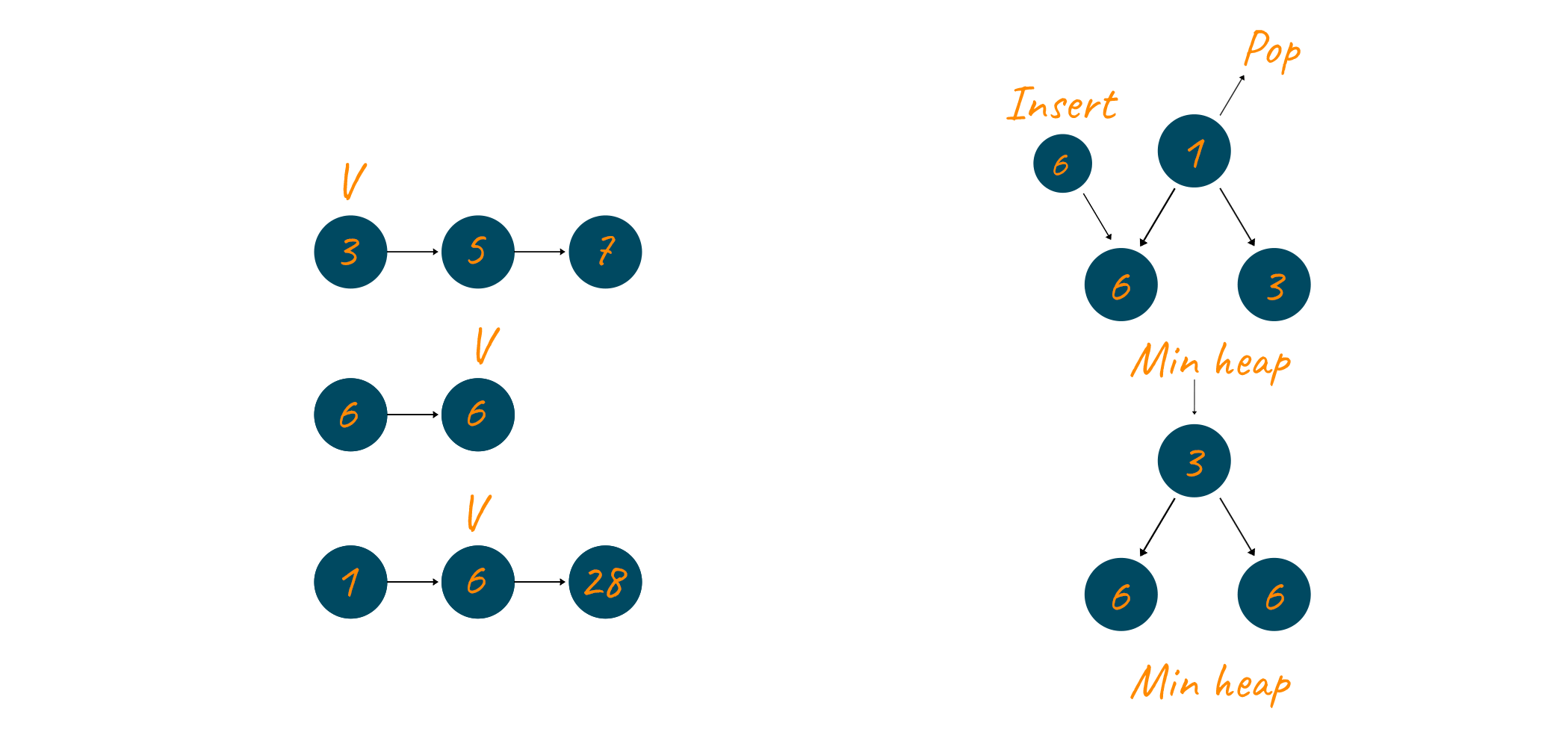
Now, 3 is now extracted from the min-heap and inserted into the result linked list. The pointer of the first linked list is updated to now point to the next element (5) and 5 is added to the min-heap.
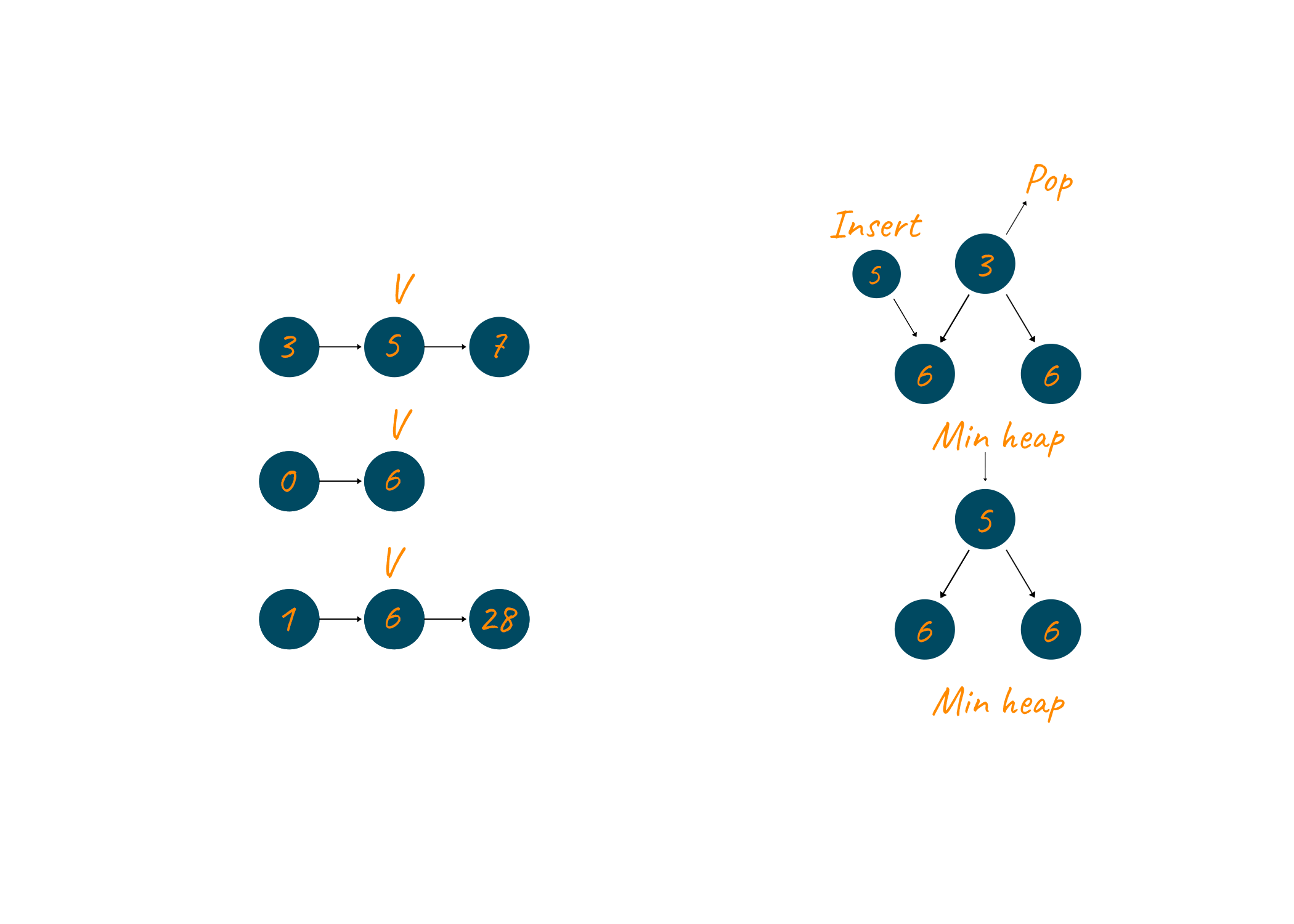
The number 5 is now extracted and it is added to the result linked list. Since 5 belonged to the first linked list therefore its pointer is updated to point to the next element (7) and this element is added to the min-heap.
The root node, 6, is again extracted and added to the min-heap. The second linked list’s pointer is updated since no element is present in this linked list therefore no element is added to the min-heap at this step.
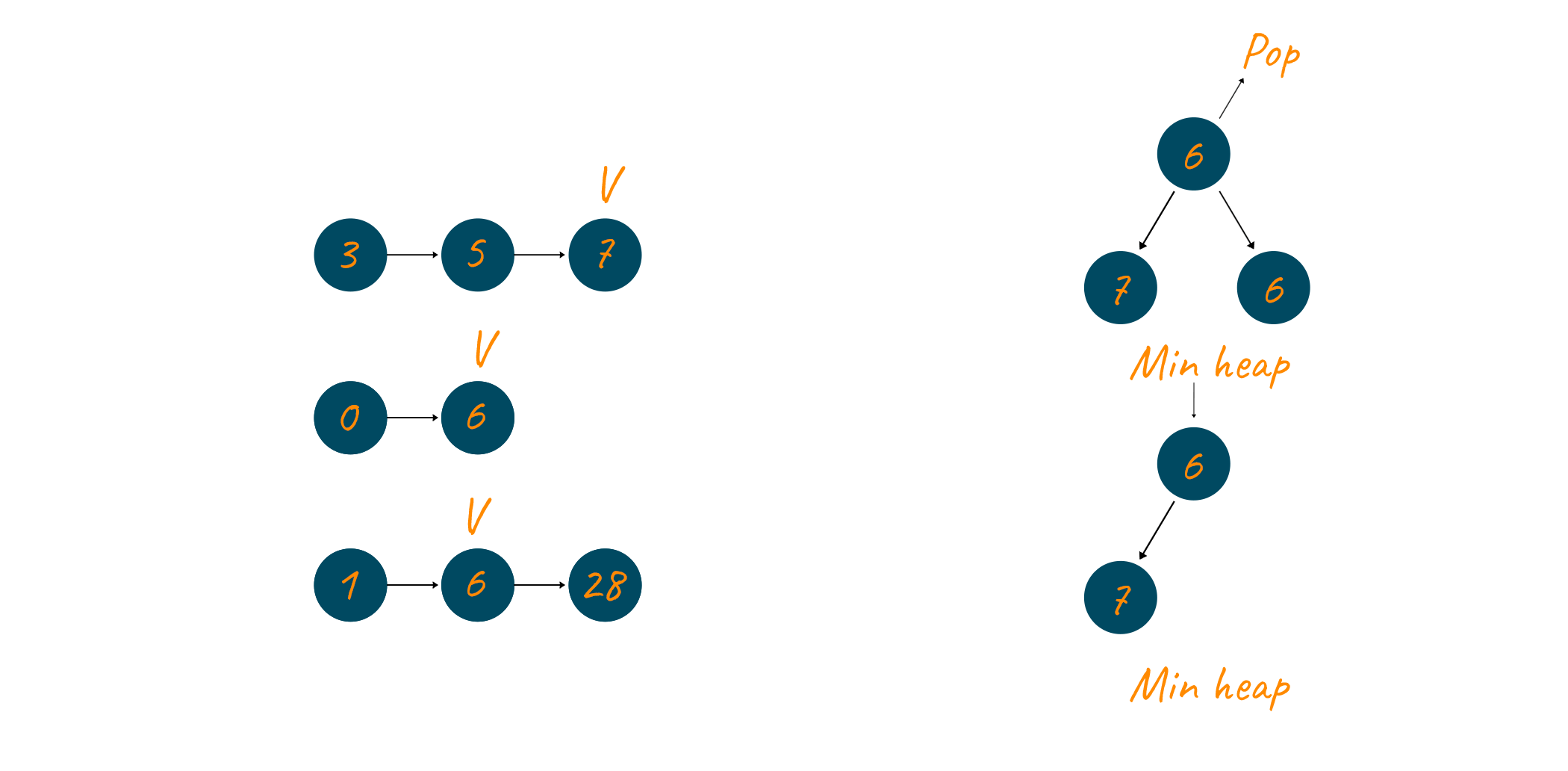
The number 6, this time from the third linked list is removed from the min-heap. The pointer of the third linked list is updated and the number 28 is added to the min-heap.
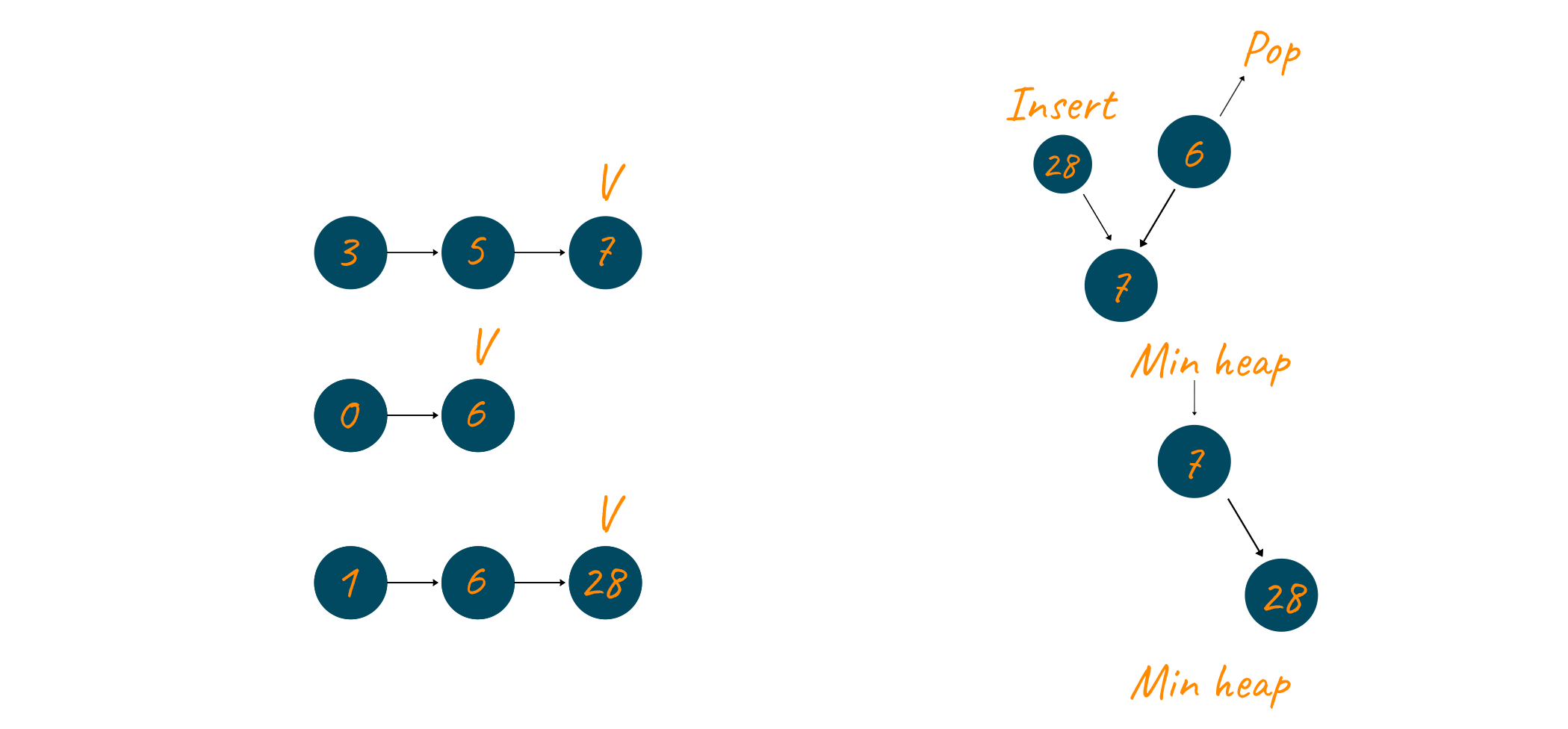
This time the number 7 is popped and the pointer of the first linked list is updated. Since this time also there are no more elements left in the first linked list, therefore, no element is inserted into the min-heap.
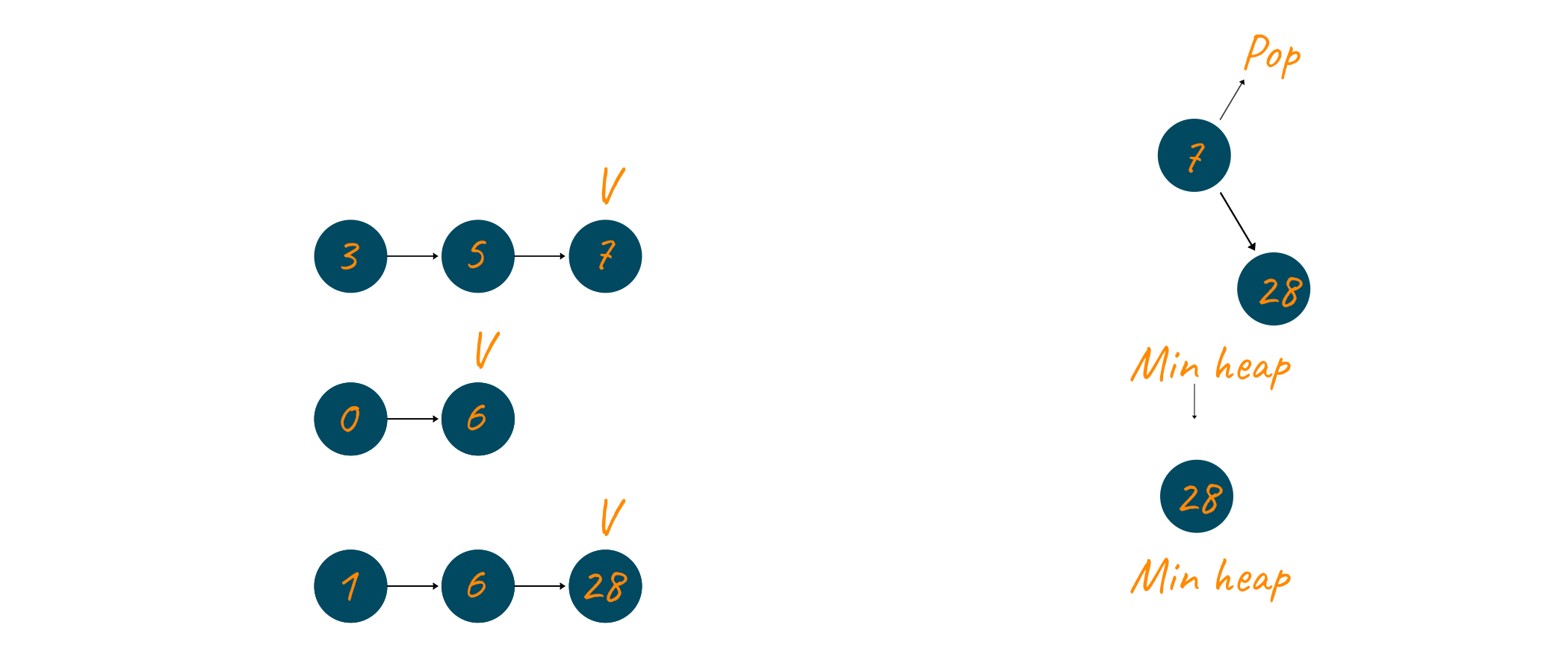
Now only one element is left in the min-heap and that element, 28, is extracted. The pointer of the third linked list is updated and because no more elements are present in the linked list that is why none are inserted.
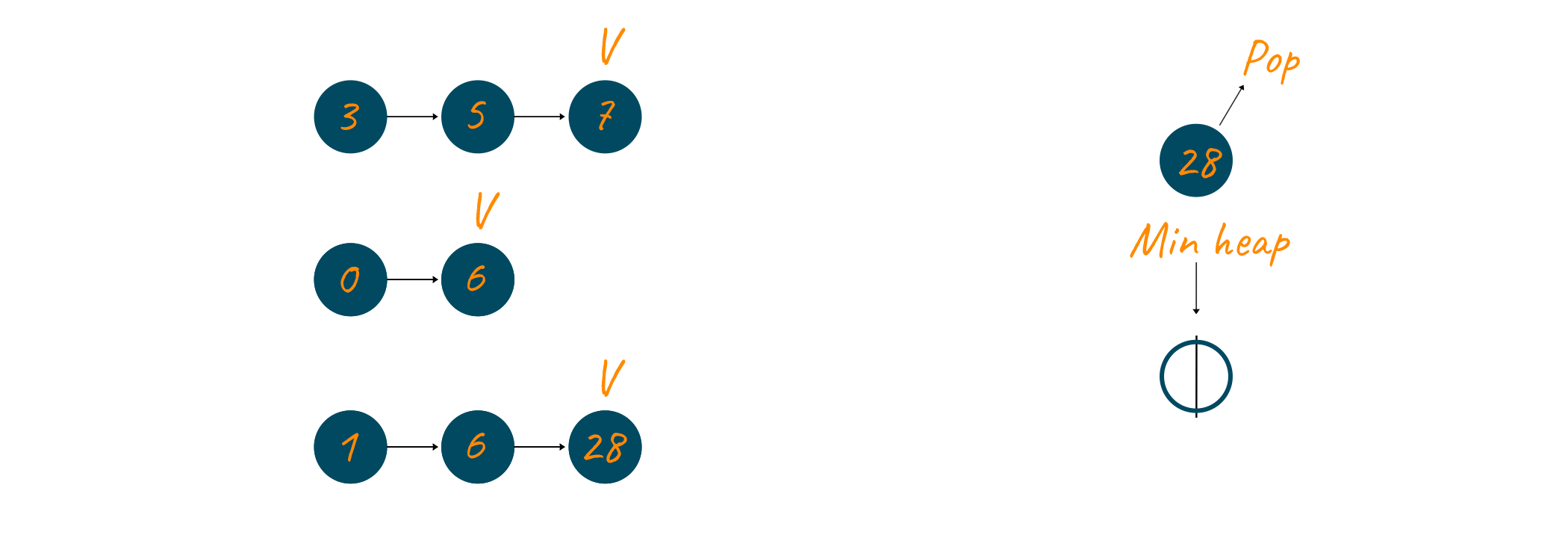
At this point the min-heap is empty and we get the result linked list as our merged linked list. At the end of this algorithm, the result linked list looks like this.

Implementation in Java
Here is the complete code in Java to merge K sorted lists using min heap:
import java.util.PriorityQueue; class Node{ int data; Node next; Node(int val){ data=val; next=null; } } public class mergeKSortedList { //function to merge k sorted linked lists. static public Node merge(Node[] arr,int k){ //PriorityQueue 'pq' implemented as min heap using lambda expression PriorityQueue<Node> pq=new PriorityQueue<>((a,b)->{ return a.data-b.data; }); //Pushing the head nodes of all //the k lists in 'pq' for(int i=0;i<k;i++){ if(arr[i]!=null){ pq.add(arr[i]); } } //Handling the case when k=0 or lists are empty. if(pq.isEmpty()) return null; //Creating dummy node Node dummy=new Node(-1); Node last=dummy; //Run while loop till priorityQueue(pq) is not empty while(!pq.isEmpty()){ //Get the top element of 'pq' //which is the minimum of all existing nodes. Node curr=pq.remove(); //Add top element of 'pq' // to the resultant merged list last.next=curr; last=last.next; // Check if there is a node // next to the 'top' node // in the list of which 'top' // node is a member if(curr.next!=null){ pq.add(curr.next); } } //return the next of dummy node // which the actual head of merged list. return dummy.next; } //function to print the sorted linked list static void printList(Node head){ while(head!=null){ System.out.print(head.data+" -> "); head=head.next; } System.out.print("none"); } public static void main(String[] args) { //Number of linked lists to be merged. int k=3; //An array of Node type storing head node of linked lists. Node[] arr=new Node[k]; //Linked List 1: 3->5->7 arr[0]=new Node(3); arr[0].next=new Node(5); arr[0].next.next=new Node(7); //Linked List 2: 0->6 arr[1]=new Node(0); arr[1].next=new Node(6); //Linked List 3: 1->6->28 arr[2]=new Node(1); arr[2].next=new Node(6); arr[2].next.next=new Node(28); //Calling the merge function to merge all the linked lists Node head=merge(arr,k); printList(head); } }
Implementation in C++
The following is the C++ program to merge K sorted lists:
#include <bits/stdc++.h> using namespace std; struct Node { int data; struct Node* next; }; struct Node* newNode(int data) { struct Node* new_node = new Node(); new_node->data = data; new_node->next = NULL; return new_node; } // 'compare' function used to build // up the priority queue struct compare { bool operator()( struct Node* a, struct Node* b) { return a->data > b->data; } }; // Function to merge k sorted linked lists struct Node* mergeKSortedLists( struct Node* arr[], int k) { // Priority_queue 'pq' implemented // as min heap with the help of // 'compare' function priority_queue<Node*, vector<Node*>, compare> pq; // Push the head nodes of all // the k lists in 'pq' for (int i = 0; i < k; i++) if (arr[i] != NULL) pq.push(arr[i]); // Handles the case when k = 0 // or lists have no elements in them if (pq.empty()) return NULL; struct Node *dummy = newNode(0); struct Node *last = dummy; // Loop till 'pq' is not empty while (!pq.empty()) { // Get the top element of 'pq' struct Node* curr = pq.top(); pq.pop(); // Add the top element of 'pq' // to the resultant merged list last->next = curr; last = last->next; // Check if there is a node // next to the 'top' node // in the list of which 'top' // node is a member if (curr->next != NULL) // Push the next node of top node // in 'pq' pq.push(curr->next); } // Address of head node of the required merged list return dummy->next; } // Function to print the linked list void printList(struct Node* head) { while (head != NULL) { cout << head->data << " "; head = head->next; } } int main() { // Number of linked lists int k = 3; // Number of elements in each list int n = 4; // An array of pointers storing the head nodes of the linked lists Node* arr[k]; arr[0] = newNode(1); arr[0]->next = newNode(3); arr[0]->next->next = newNode(5); arr[0]->next->next->next = newNode(7); arr[1] = newNode(2); arr[1]->next = newNode(4); arr[1]->next->next = newNode(6); arr[1]->next->next->next = newNode(8); arr[2] = newNode(0); arr[2]->next = newNode(9); arr[2]->next->next = newNode(10); arr[2]->next->next->next = newNode(11); struct Node* head = mergeKSortedLists(arr, k); printList(head); return 0; }
Implementation in Python
In Python, we use the built-in heapq module:
import heapq from heapq import heappop, heappush # Node of linked list class Node: def __init__(self, data, next=None): self.data = data self.next = next def __lt__(self, other): return self.data < other.data # function to print contents of a linked list def printList(node): while node: print(node.data, end=' —> ') node = node.next print('None') def mergeKLists(lists): # create a min-heap using the first node of each list pq = [x for x in lists] heapq.heapify(pq) head = last = None while pq: # extract node from the min-heap min = heappop(pq) # add the minimum node to the output list if head is None: head = min last = min else: last.next = min last = min # take the next node from the "same" list and insert it into the min-heap if min.next: heappush(pq, min.next) # return head node of the merged list return head k = 3 lists = [None] * k lists[0] = Node(3) lists[0].next = Node(5) lists[0].next.next = Node(7) lists[1] = Node(0) lists[1].next = Node(6) lists[2] = Node(1) lists[2].next = Node(6) lists[2].next.next = Node(28) # Merge all lists head = mergeKLists(lists) printList(head)
Output:
0 —> 1 —> 3 —> 5 —> 6 —> 6 —> 7 —> 28 —> None
Time Complexity
This method has a time complexity of O(n.log(k)). Where n is the total number of elements across all the lists and k is the number of linked lists in the question. Let's now discuss how this complexity is calculated.
A min-heap is essentially a complete binary tree and a complete binary tree has 1 + floor( log x) levels. Where x is the total number of elements in the tree. Since in this algorithm, the min-heap can have at max k element at any given instant, therefore, x is equal to k here.
So, in this case, we are going to have 1+ floor(log k) levels, which is O(log k). Now for all the elements (n), we are going to perform insertion in the binary tree. The cost insertion for an element in a heap is equal to the number of levels in the heap.
Since the number of levels is log k in this case, therefore the cost of insertion per element is log k. Now for adding n elements the total cost will be n log k.
Let us now come to the removal of elements. Removal also takes the same time as insertion in a binary heap, therefore, the time required to remove n elements from the binary heap is n log k. Now the total time to remove and insert n elements in a binary heap is equal to 2 n log k. Therefore, the time complexity of this algorithm calculates to be O(n.log(k))
A major advantage of this method is its adaptability. This method can be appointed to merge K-sorted arrays as well, with some small tweaks here and there. This method works well even when all the linked lists are not of the same size, which some of the other methods fail to achieve.
Merge k-sorted lists using the Divide and Conquer
We can merge k sorted lists using divide and conquer involves a recursive technique that merges pairs of linked lists periodically until all k lists have been merged into a single sorted list can be used to address this problem.
In Python, we can iteratively split the list of linked lists into smaller sub-problems until we only have two linked lists. We then use a simple merging technique to combine these two linked lists and return the result. We repeat this method until all of the linked lists have been combined into a single sorted list. Learn more about Divide & Conquer algorithm in Python here.
Here's an example implementation in Python:
def mergeKLists(lists): if len(lists) == 0: return None if len(lists) == 1: return lists[0] if len(lists) == 2: return mergeTwoLists(lists[0], lists[1]) mid = len(lists) // 2 left = mergeKLists(lists[:mid]) right = mergeKLists(lists[mid:]) return mergeTwoLists(left, right) def mergeTwoLists(l1, l2): if not l1: return l2 if not l2: return l1 if l1.val < l2.val: l1.next = mergeTwoLists(l1.next, l2) return l1 else: l2.next = mergeTwoLists(l1, l2.next) return l2
In this approach, the length of the input-linked list is first established. We return None if the length is zero. We just put a linked list into the list if the length is one. If the length is 2, we use a simple merging technique called'mergeTwoLists' to merge the two linked lists and provide the result.
When the length of the list approaches 2, we partition it recursively into two sub-problems until we only have two linked lists. We then use the'mergeTwoLists' method to combine these two linked lists and return the result. This technique is repeated until all linked lists have been merged into a single sorted list.
This technique has a temporal complexity of O(n log k), where n is the total number of items in all linked lists and k is the number of linked lists. The space complexity is O(log k) due to the recursive call stack.
Conclusion
This problem tests a candidate's problem-solving skills and his or her grasp on the concepts of linked list and heap. We highly encourage you to have a good grasp of major data structures. Also, if you need help with your data structures assignments then our experts are available 24/7. In this article, we first discussed the problem statement.