Longest Consecutive Sequence (with C++, Java & Python code)

There are several complex programming problems that have very interesting solutions. One such problem is the Longest Consecutive Sequence, which we will learn about in this article, with an algorithm to solve it. Learning some such algorithms may help one to increase problem-solving skills and crack many technical interviews with ease.

What is the Longest Consecutive Sequence?

The Longest Consecutive Sequence is a continuous sequence of values, a series of numbers from a specified list or array with no gaps or interruptions. In this context, " longest " refers to the most extended sequence in the selected index or array. For example, the most extended consecutive series in a given list will be [5, 6, 7, 8, 9], containing five successive integers.

The simplest way to discover the LCS is to reorder the list in ascending order and traverse through it while keeping track of the length of the current sequence. Another method is to use a hash table or set to record the list elements and then a loop to check if each component is preceded and succeeded by a consecutive piece.

These two methods can help you keep track of the length of the current sequence and the longest sequence you've ever recorded. 

Now we know what it is, let's look at the problem statement: "If we are given an unsorted array of integers, we have to find the longest consecutive sequence in the array."

Algorithm

The following is the step-by-step algorithm to solve LCS problem:

1. First, sort the array using any one of the in-place sorting algorithms.
2. Then declare two variables to track the current length and maximum length of consecutive numbers found in the array.
3. If the length of the array is zero then return zero as the output
4. Else, iterate through the array and check whether the next element to the current element is consecutive and increment the current value.
5. If the next element is not consecutive to the current element then stop the iteration.
6. Compare and check the current and longest, and store the maximum value in the longest.
7. Repeat the steps till the length of the array.
8. The final value in the longest variable is the result.

Example of Longest Consecutive Sequence

To understand the working of our approach better, let us take an example and look into the step-by-step execution.

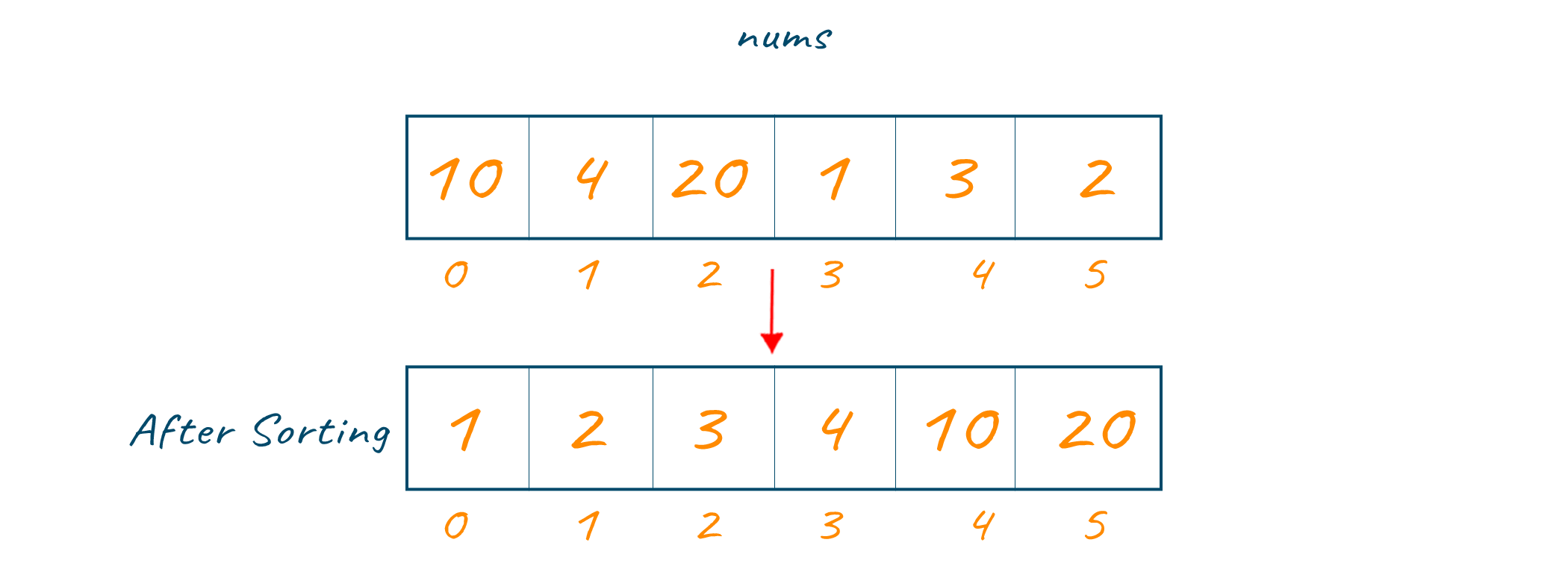
In the first step, the input is sorted in increasing order.

Then at each step, the current element is checked with the next element to verify whether it is a consecutive number. Then the current and longest variables are incremented. Finally, the maximum length is returned as output. Refer to the below image for a better and clear understanding of the steps.

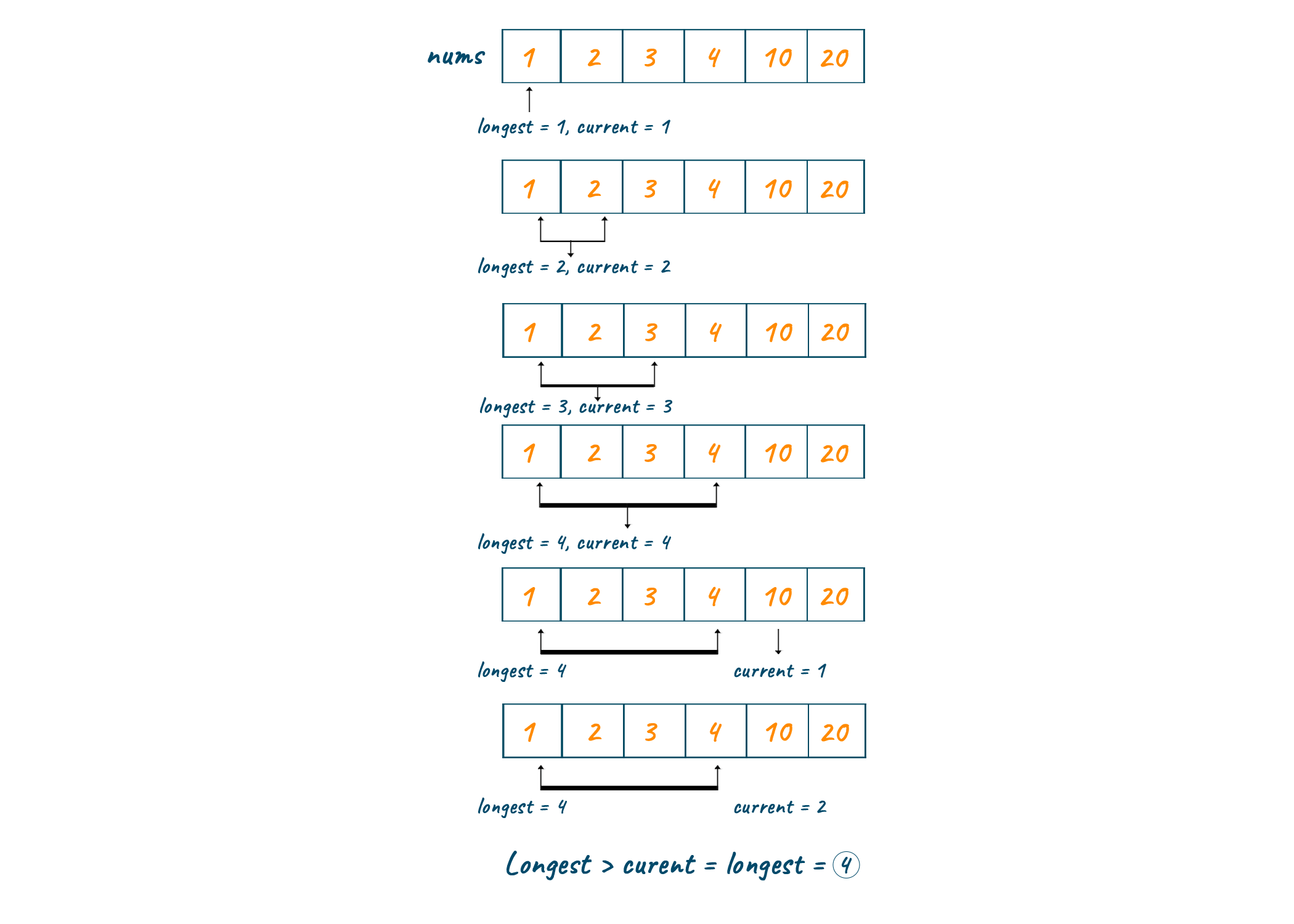
Longest Consecutive Sequence in Java

The following code in Java will help us find the LCS in ana array:

import java.util.*;
public class Solution
{
public static int longestConsecutive(int[] nums) {
  if (nums.length == 0) return 0;
  Arrays.sort(nums);
  int longSequence = 1;
  int currentSequence = 1;
  for (int i = 1; i < nums.length; i++) {
    if (nums[i] != nums[i-1]) {
      if (nums[i] == nums[i-1]+1) {
        currentSequence += 1;
      }
      else {
        longSequence = Math.max(longSequence, currentSequence);
        currentSequence = 1;
      }
    }
  }
  return Math.max(longSequence, currentSequence);
}
public static void main(String[] args) {
  int nums[]={10,4,20,1,3,2};
  System.out.println(longestConsecutive(nums));
}
}

Output:

4

Longest Consecutive Sequence in C++

Below is the C++ Program to find Longest Consecutive Sequence in an array:

#include <bits/stdc++.h>
using namespace std;
 

int findLongestConseqSubseq(int arr[], int n) {
    unordered_set<int> S;
    int ans = 0;
    for (int i = 0; i < n; i++)
        S.insert(arr[i]);
    // check each possible sequence from the start then update optimal length
    for (int i = 0; i < n; i++) {
        // if current element is the starting element of a sequence
        if (S.find(arr[i] - 1) == S.end()) {
            // Then check for next elements
            int j = arr[i];
            while (S.find(j) != S.end())
                j++;
            // update length if new length is more
            ans = max(ans, j - arr[i]);
        }
    }
    return ans;
}
 
int main() {
    int n = 7;
    int arr[] = { 10,4,20,1,3,2 };
    cout << "Length of the Longest contiguous subsequence is :"
         << findLongestConseqSubseq(arr, n);
    return 0;
}

Output:

4

Time  & Space complexity

The execution time varies according to the input values and has to be analyzed for the solution we build to check the efficiency of the approach. The respective time complexity to find the Longest Consecutive Sequence will be O(nlogn). Since the sorting algorithm takes the logarithmic time complexity and we are iterating through a single loop.

The extra space required to execute the program is the space complexity of the program. In our case, we are using the in-place sorting algorithm for arranging the elements and no new array is used so the space complexity will be O(1). That is constant space complexity which remains constant irrespective of the input size.

Longest Consecutive Sequence using Hashing

To find the most extended consecutive sequence using Hashing, we use a set to store the elements of the list and check if each component has a next part, either before or after it.

An empty set is created using hash_set, and all the elements of the given list are inserted into it. Then we initialize two variables, one to store the length of the most extended consecutive sequence, called max_len, and the other to keep the size of the current arrangement being checked, labeled curr_len. 

We then iterate through the hash set elements and check if each list component has a consecutive aspect before and after it. If the part has straight features, we increment the curr_len variable. Otherwise, we update max_len if curr_len is greater than max_len and reset curr_len to 1. Finally, we return max_len as the length of the most extended consecutive sequence.

Below is a Python code to showcase this approach:

def longest_consecutive_sequence(arr):
    hash_set = set(arr)
    max_len = 0
    for num in hash_set:
        If num-1  not in hash_set:
            curr_len = 1
            while num+1 in hash_set:
                curr_len += 1
                num += 1
            max_len = max(max_len, curr_len)
    return max_len

This function takes a list ‘arr’ as input and returns the length of the longest consecutive sequence in the list using the hashing approach.

Find the LCS using Priority Queue

The approach we shall present here may be used to find the longest sequence in the queue.

The first step is to construct a min heap priority queue, which is described as a data structure used to store things in a certain order. The min heap priority queue is a sequence that saves the arrangement's smallest element. The elements are subsequently added to the input list and, as a result, to the line.

The variables "max_len" and "curr_len" are set to their default values. The variable max_len holds the longest serial sequence discovered to date, whereas curr_len holds the length of the current serial series. The variable "curr_len" is set to 1 because it is the smallest value.

While eliminating an element from the priority queue, we compare the last part. The test is to see if the current element equals the previous component plus one, in which case the variable curr_len rises. If not, the variables max_len and curr_len are set to the maximum extent and reset to 1. 

The operation is repeated until the priority queue is empty, at which point max_len yields the length of the list's longest stretched sequence.

Here is the Python code to implement this approach:

def longest_consecutive_sequence(arr):
    heap = []
    for num in arr:
        heapq.heappush(heap, num)
    max_len = 0
    curr_len = 1
    while heap:
        num = heapq.heappop(heap)
        if heap and num == heap[0]-1:
            curr_len += 1
        elif curr_len > 1:
            max_len = max(max_len, curr_len)
            curr_len = 1
    if curr_len > 1:
        max_len = max(max_len, curr_len)
    return max_len

This function takes a list arr as input and returns the length of the longest consecutive sequence in the list using the priority queue approach.

Conclusion

In this article, we solve the Longest Consecutive Sequence problem in programming using different approaches. LCS is particularly useful in cryptography for generating random number sequences in encryption and decryption procedures. Still, if you are confused, our online Python tutors are available 24/7 to assist you.