Sorting in computer science refers to the process of arranging data in a specific order. In this article, we will learn about Insertion Sort thoroughly, with implementation in C++.
Insertion Sort Algorithm
Sorting is a fundamental operation in computer science that every beginner should be good at, often required in databases, search algorithms, computer graphics, and data analysis. There are many different algorithms that can be used for sorting, each with its own advantages and disadvantages. The most popular sorting techniques include heap sort, bubble sort, selection sort, or merge sort.
Insertion sort is a simple and efficient sorting algorithm that sorts an array or a list of elements by repeatedly inserting each unsorted element into its appropriate position within the sorted portion of the list. The algorithm works by iterating through the list, starting with the second element, and comparing each element with the elements that come before it.
Step-by-Step Approach
Here are the detailed steps of the insertion sort algorithm:
-
Start with the second element of the list, assuming the first element is already sorted.
-
Compare the second element with the first element. If the second element is smaller, swap the two elements.
-
Move on to the third element, compare it with the second element, and then with the first element. If it is smaller than either of these, swap it with the appropriate element(s).
-
Repeat this process for each subsequent element in the list, comparing it with all of the elements that come before it and inserting it into its correct position within the sorted portion of the list.
-
Once all the elements have been processed, the list will be fully sorted.
Insertion Sort Example
Let's consider the following example for understanding insertion sort thoroughly.
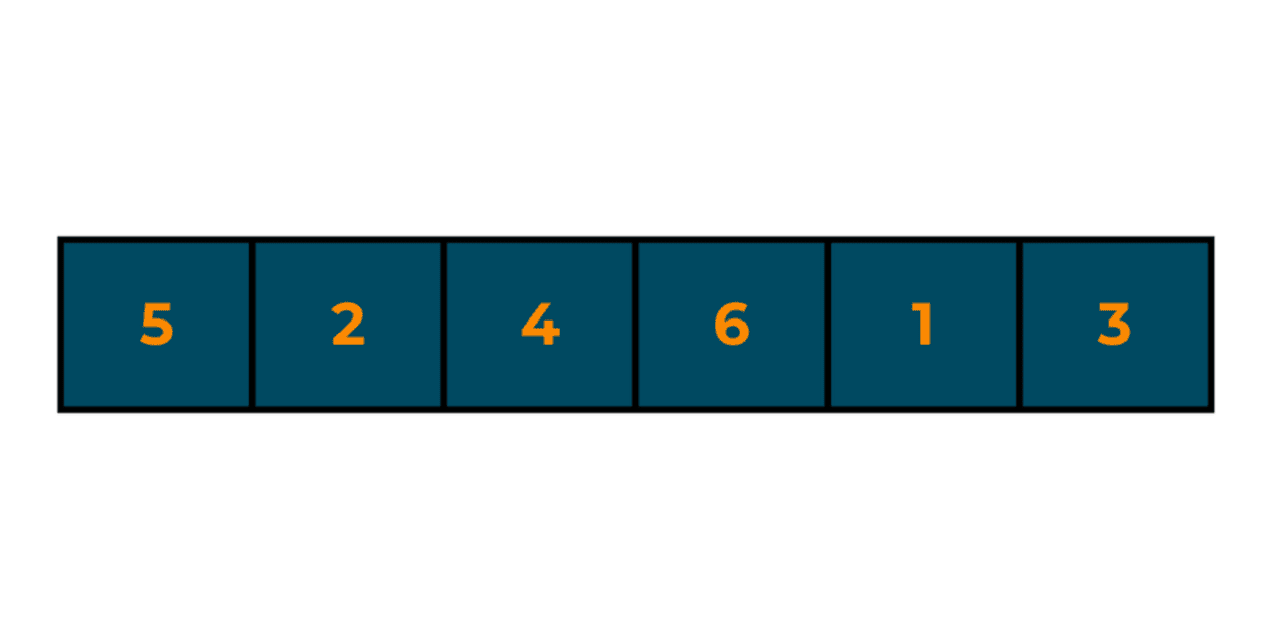
Start with the second element (2). Compare the second element (2) with the first element (5). Since 2 is smaller, swap the two elements.
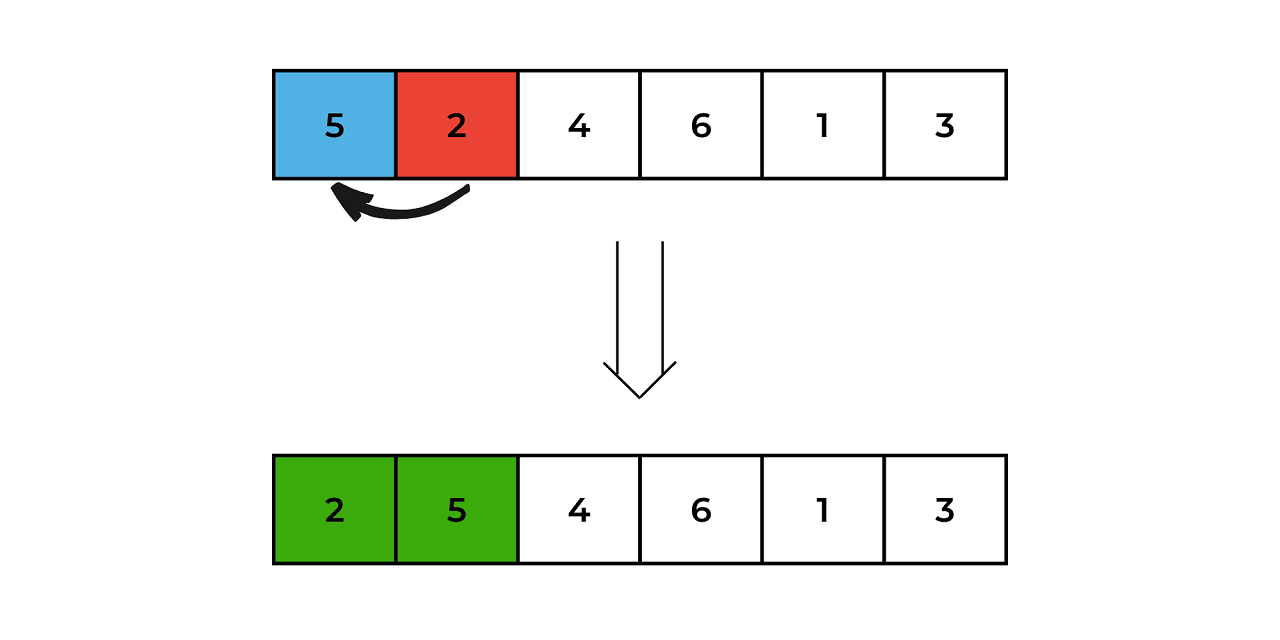
Move on to the third element (4), and compare it with the second element (5). Since 4 is smaller, swap the two elements. Further compare it with the first element(2), since 4 is larger we leave it as it is.
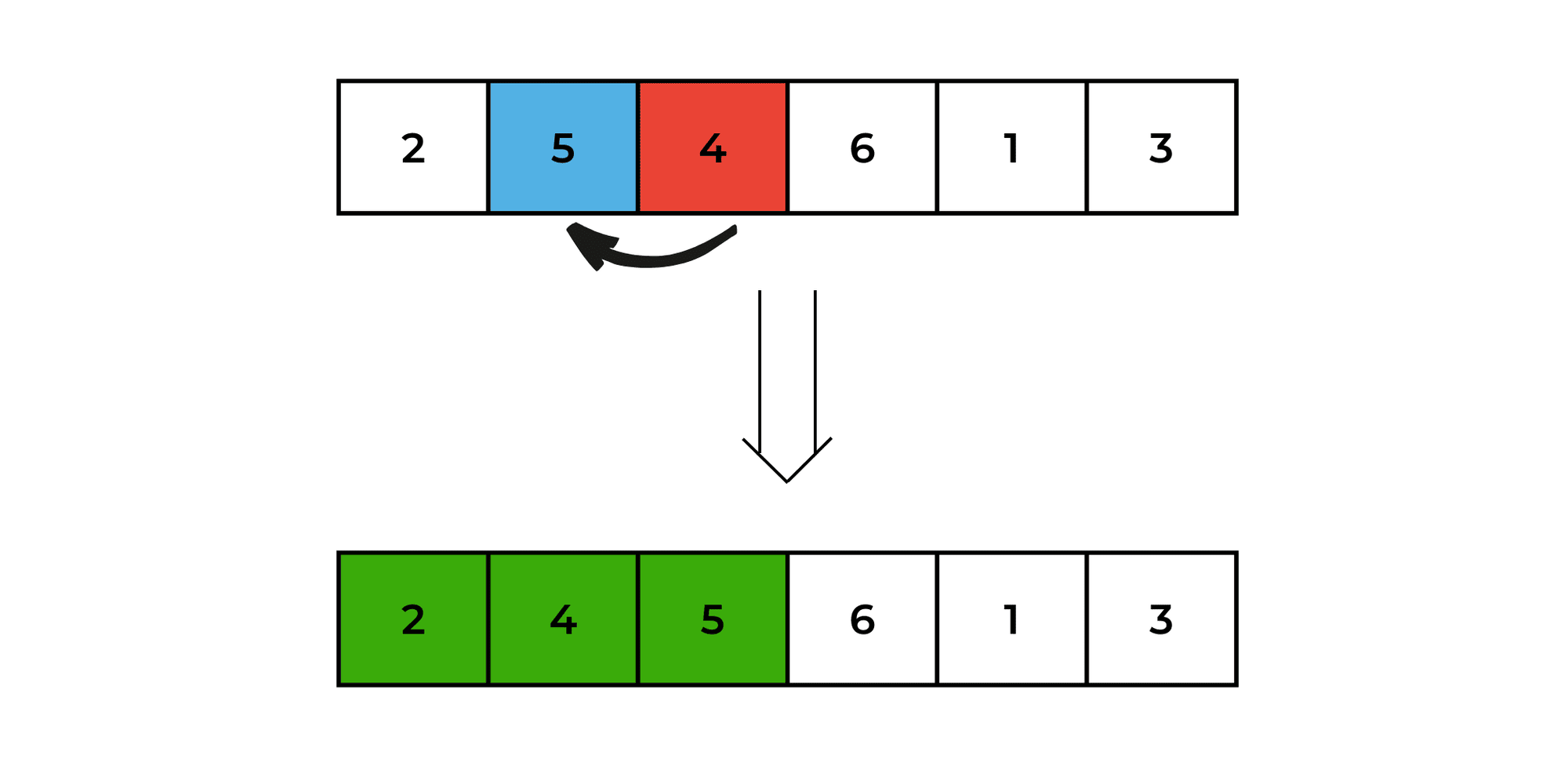
Move on to the fourth element (6), and compare it with the third element (5). Since 6 is larger, leave it where it is.
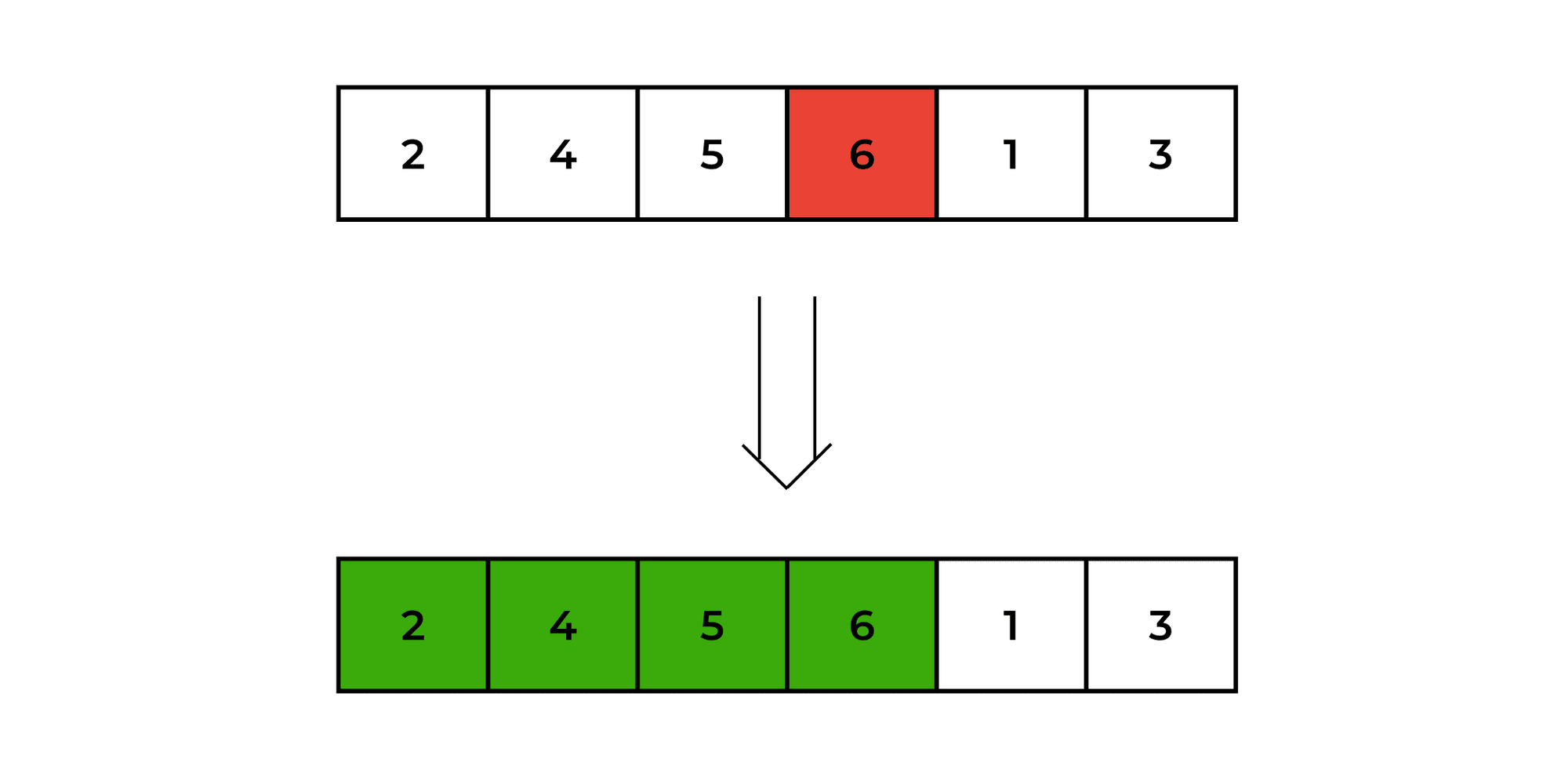
Move on to the fifth element (1), and compare it with the fourth element (6). Since 1 is smaller, swap it with the fourth element (6), and then compare it with the third element (5).
Since 1 is smaller, swap it with the third element (5), and then compare it with the second element (4). Since 1 is smaller, swap it with the second element (4), and then compare it with the first element (2). Since 1 is smaller, swap it with the first element (2).
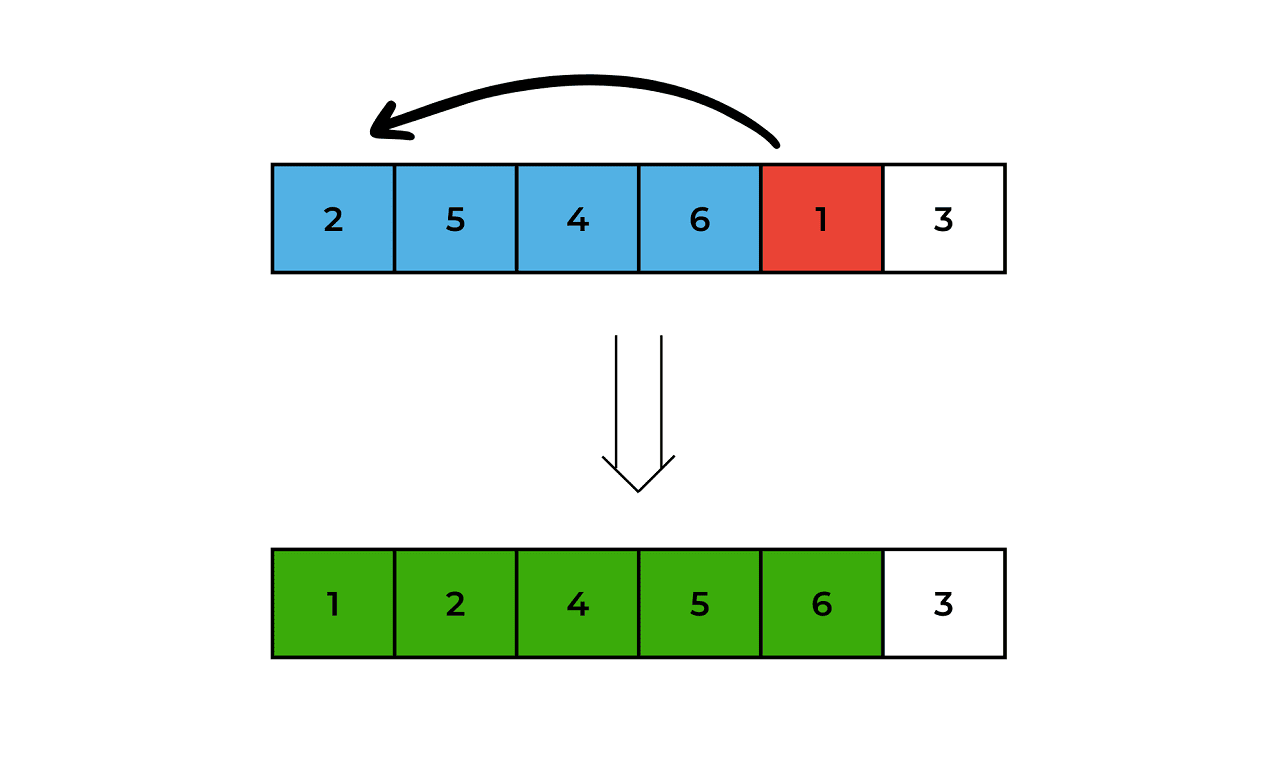
Move on to the sixth element (3), and compare it with the fifth element (6). Since 3 is smaller, swap it with the fifth element (6), and then compare it with the fourth element (5). Since 3 is smaller, swap it with the fourth element (5), and then compare it with the third element (4). Since 3 is smaller, swap it with the third element (4), and then compare it with the second element (2). Since 3 is larger, leave it where it is.
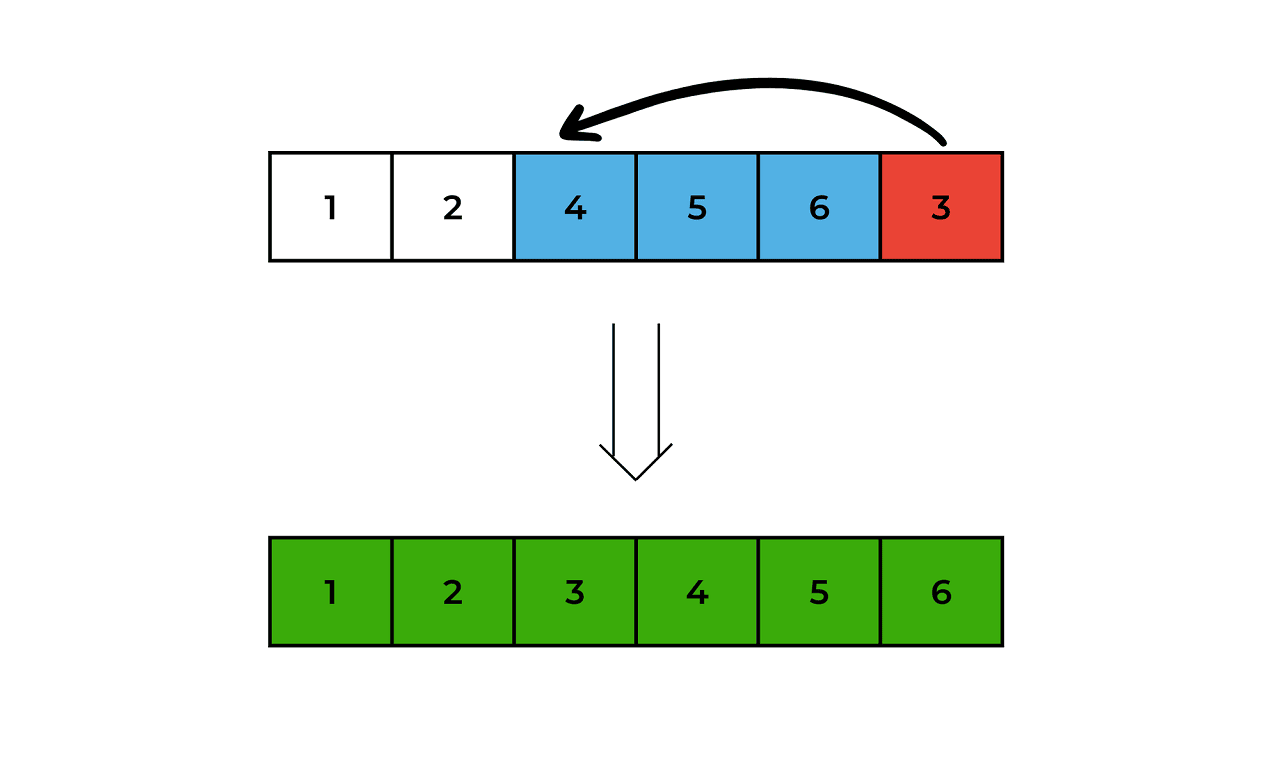
The array is now fully sorted.
So the final sorted array is 1, 2, 3, 4, 5, 6.
C++ code for Insertion Sort
Below is the complete program to implement insertion sort in C++. In this implementation, the insertionSort function takes an array arr of size n as input, and sorts it using the insertion sort algorithm. The sorted array is then printed out in the main function.
Ascending order:
#include <iostream> using namespace std; void insertionSort(int arr[], int n) { int i, j, key; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } } int main() { int arr[] = {5, 2, 4, 6, 1, 3}; int n = sizeof(arr) / sizeof(arr[0]); cout << "Original array: "; for (int i = 0; i < n; i++) { cout << arr[i] << " "; } cout<<endl; insertionSort(arr, n); cout << "Sorted array: "; for (int i = 0; i < n; i++) { cout << arr[i] << " "; } cout << endl; return 0; }
Output:
Original array: 5 2 4 6 1 3 Sorted array: 1 2 3 4 5 6
Time Complexity: O(N^2), where N is the number of nodes
Space Complexity: O(1), we do not require any extra space.
Descending Order:
#include <iostream> using namespace std; void insertionSort(int arr[], int n) { int i, j, key; for (i = 1; i <n ; i++) { key = arr[i]; j = i - 1; while (j >=0 && arr[j] < key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } } int main() { int arr[] = {5, 2, 4, 6, 1, 3}; int n = sizeof(arr) / sizeof(arr[0]); cout << "Original array: "; for (int i = 0; i < n; i++) { cout << arr[i] << " "; } cout<<endl; insertionSort(arr, n); cout << "Sorted array: "; for (int i = 0; i < n; i++) { cout << arr[i] << " "; } cout << endl; return 0; }
Output:
Original array: 5 2 4 6 1 3 Sorted array: 6 5 4 3 2 1
Time Complexity: O(N^2), where N is the number of nodes
Space Complexity: O(1), we do not require any extra space.
Insertion Sort in C++ using Linked Lists
The recommended sorting method for linked lists is insertion sort, which only needs a fixed amount of extra memory for pointers and, in the worst case, has an O(n^2) time complexity.
Here's a step-by-step algorithm for insertion sort on a linked list in C++:
- If the linked list is empty or contains only one element, it is already sorted. Hence, we return the linked list's head.
- Create a new empty sorted linked list.
- Traverse the original linked list, starting from the head node.
- For each node in the original linked list, remove it from the original linked list and insert it into the correct position in the sorted linked list.
- Once all nodes have been inserted into the sorted linked list, return the head of the sorted linked list.
Below is the C++ code to implement insertion sort using linked lists.
#include <iostream> using namespace std; class Node { public: int data; Node* next; Node(int val) { data = val; next = NULL; } };
//function to print the linked list void printList(Node* head) { while (head != NULL) { cout << head->data << " "; head = head->next; } cout << endl; }
//function to insert nodes in the linked list void insertNode(Node*& head, Node* newNode) { Node* curr = head; Node* prev = NULL; while (curr != NULL && curr->data < newNode->data) { prev = curr; curr = curr->next; } if (prev == NULL) { newNode->next = head; head = newNode; } else { prev->next = newNode; newNode->next = curr; } }
//fucntion to sort the linked list void insertionSort(Node*& head) { if (head == NULL || head->next == NULL) { return; } Node* sortedList = NULL; Node* curr = head; while (curr != NULL) { Node* nextNode = curr->next; insertNode(sortedList, curr); curr = nextNode; } head = sortedList; } int main() {
//create the linked list Node* head = new Node(5); head->next = new Node(2); head->next->next = new Node(4); head->next->next->next = new Node(6); head->next->next->next->next = new Node(1); head->next->next->next->next->next = new Node(3);
//print the original linked list cout << "Original List: "; printList(head); insertionSort(head);
//print the original linked list
cout << "Sorted List: ";
printList(head);
return 0;
}
Output:
Original List: 5 2 4 6 1 3 Sorted List: 1 2 3 4 5 6
Is Insertion Sort a Stable Algorithm?
Insertion sort is a stable sorting algorithm, which means that it preserves the relative order of equal elements in the sorted array. It is also an in-place sorting algorithm, which means that it sorts the array in place without requiring any additional memory. This can be an advantage in situations where memory usage is a concern.
Advantages & Disadvantages
One of the best advantages of Insertion Sort is that is very efficient for small arrays. This is because the time complexity of insertion sort is O(n^2), which can be slower than more advanced algorithms like quicksort and mergesort for large arrays but is faster than them for small arrays.
It is also adaptive, which means that it performs well on partially sorted arrays or almost sorted arrays. In fact, for a partially sorted array, insertion sort has a time complexity of O(n), which is much faster than the O(nlogn) time complexity of most other sorting algorithms.
But that also makes it a little inefficient for large arrays. It is not suitable for random access files and parallel processing.
It is the preferred sorting algorithm for linked lists because it requires only a constant amount of additional memory for pointers and has a time complexity of O(n^2) for the worst case.
Conclusion
Overall, insertion sort is a good choice when we need to sort small arrays, partially sorted arrays, or linked lists, and when we need to perform online sorting. It is a simple and intuitive algorithm that is easy to implement and understand.








