In binary search trees (BSTs), the concept of the in-order successor plays a significant role in navigating and manipulating the tree. In this article, we will delve into the concept of traversing the in-order successor in a BST and explore various approaches to finding it.
Inorder Successor in BST
The inorder successor of a node is defined as the next node that would be visited in an inorder traversal after the given node.
Inorder traversal is a popular traversal technique used to visit nodes in a BST. In this traversal, the left subtree is traversed first, followed by the root node, and finally the right subtree. This traversal pattern visits the nodes in ascending order, making it ideal for performing operations such as searching, sorting, or evaluating expressions stored in a BST.
In the context of a BST, the in-order successor of a node is the node that follows the given node in the in-order traversal. It is the smallest node that is greater than the given node. If a node has a right subtree, its in-order successor will be the leftmost node in the right subtree. If a node does not have a right subtree, its in-order successor will be the closest ancestor whose left subtree contains the given node.
Let's consider the following Binary Search Tree (BST) as an example:
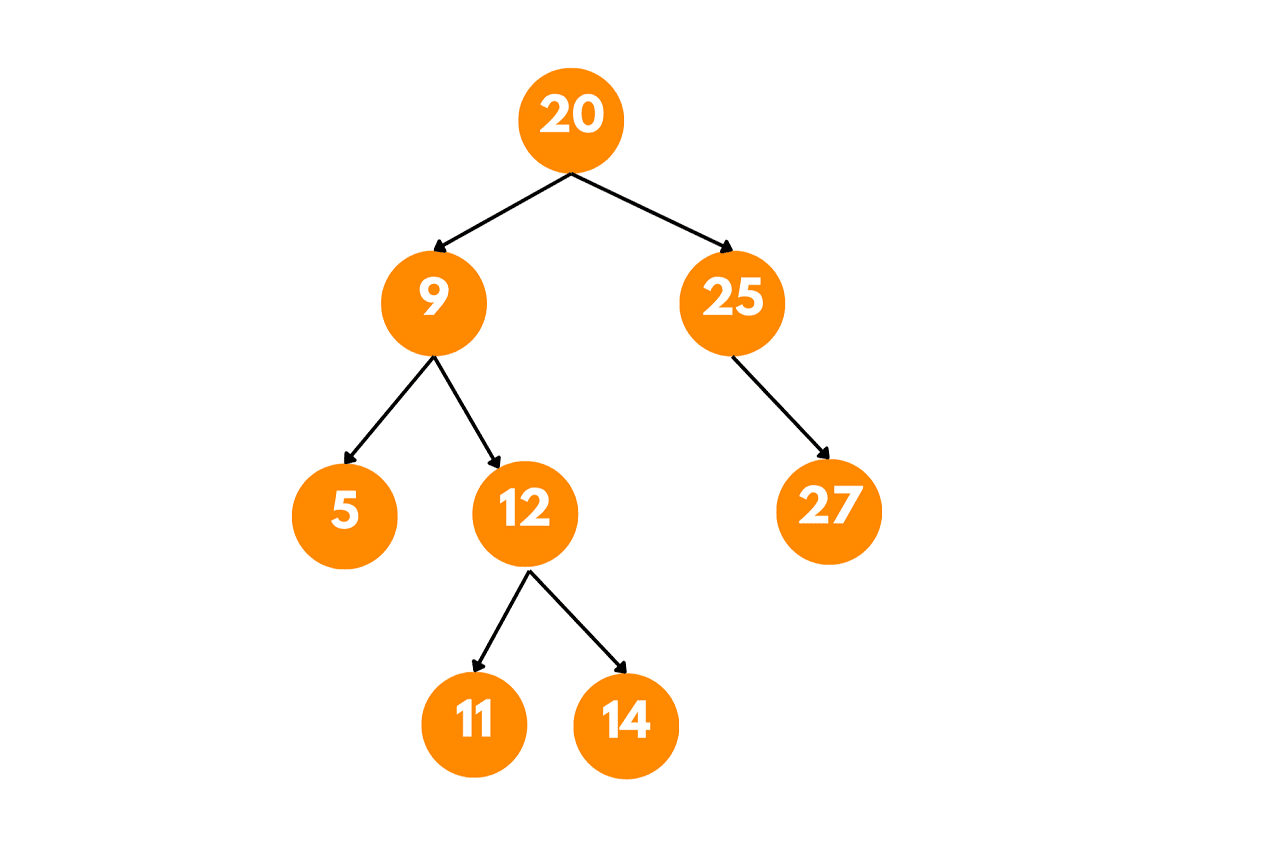
In this BST, we want to find the inorder successor of a given node.
Let's say we want to find the inorder successor of the node with value 12.
First, we start at the root of the tree, which is 20. Since 12 is less than 20, we move to the left subtree.
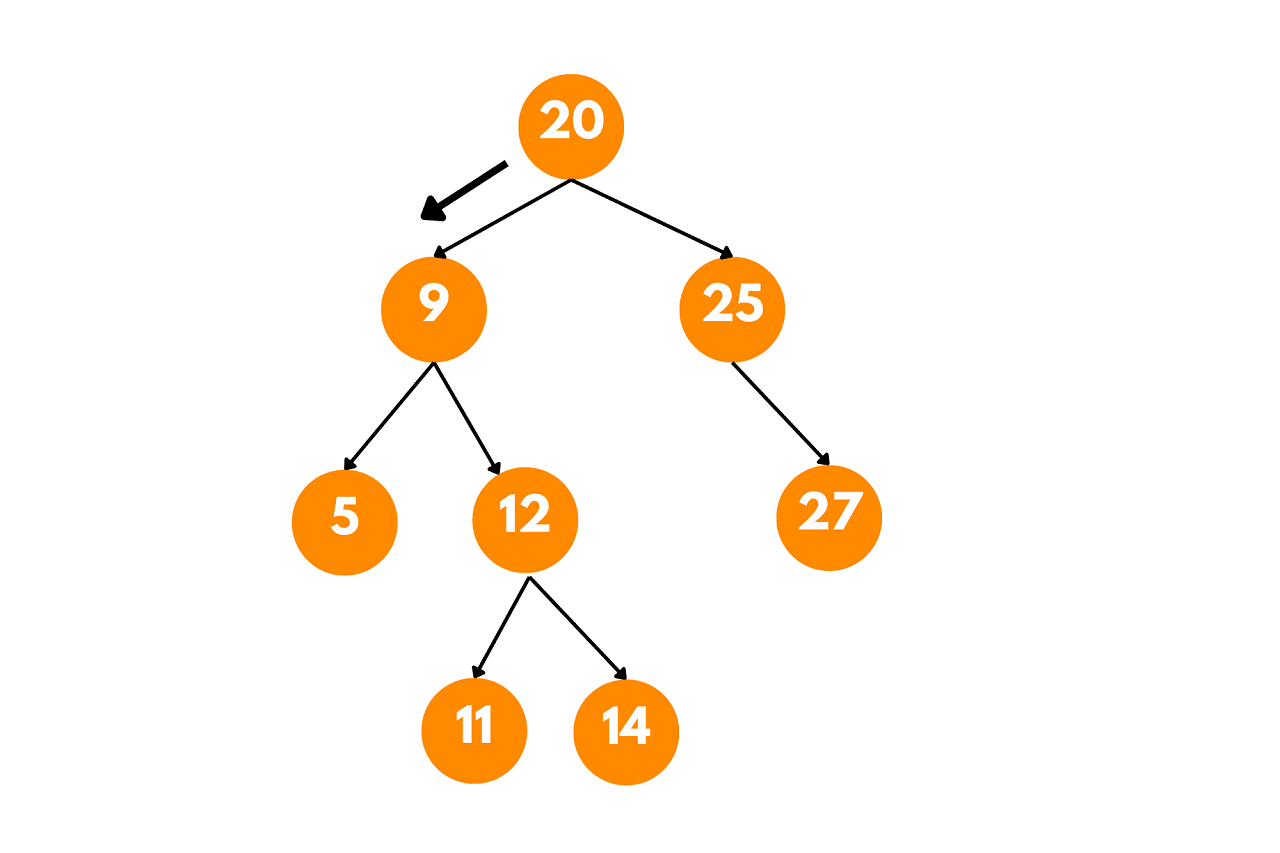
Next, we reach the node with value 9. Again, 12 is less than 9, so we move to the left subtree.
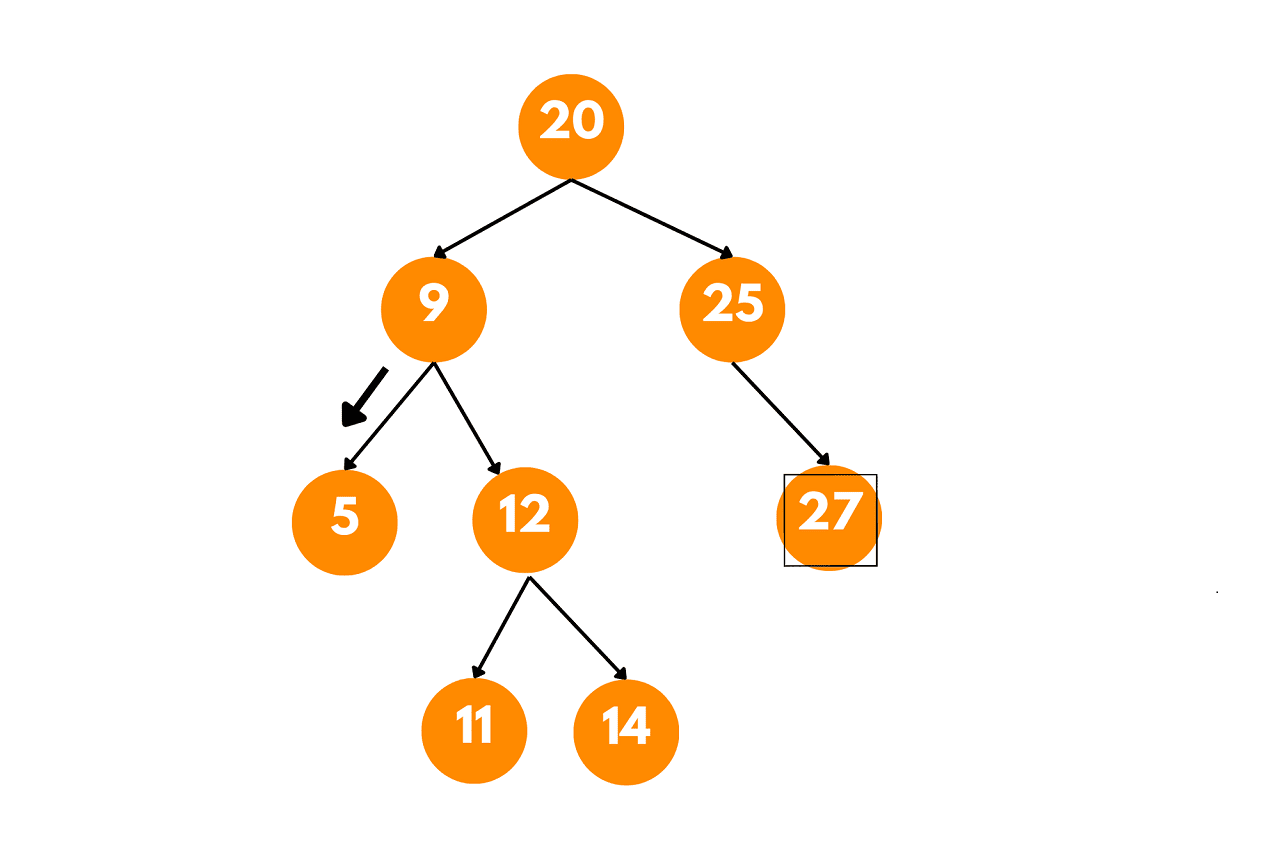
We arrive at the node with the value 5, but 12 is greater than 5, so we move to the right subtree.
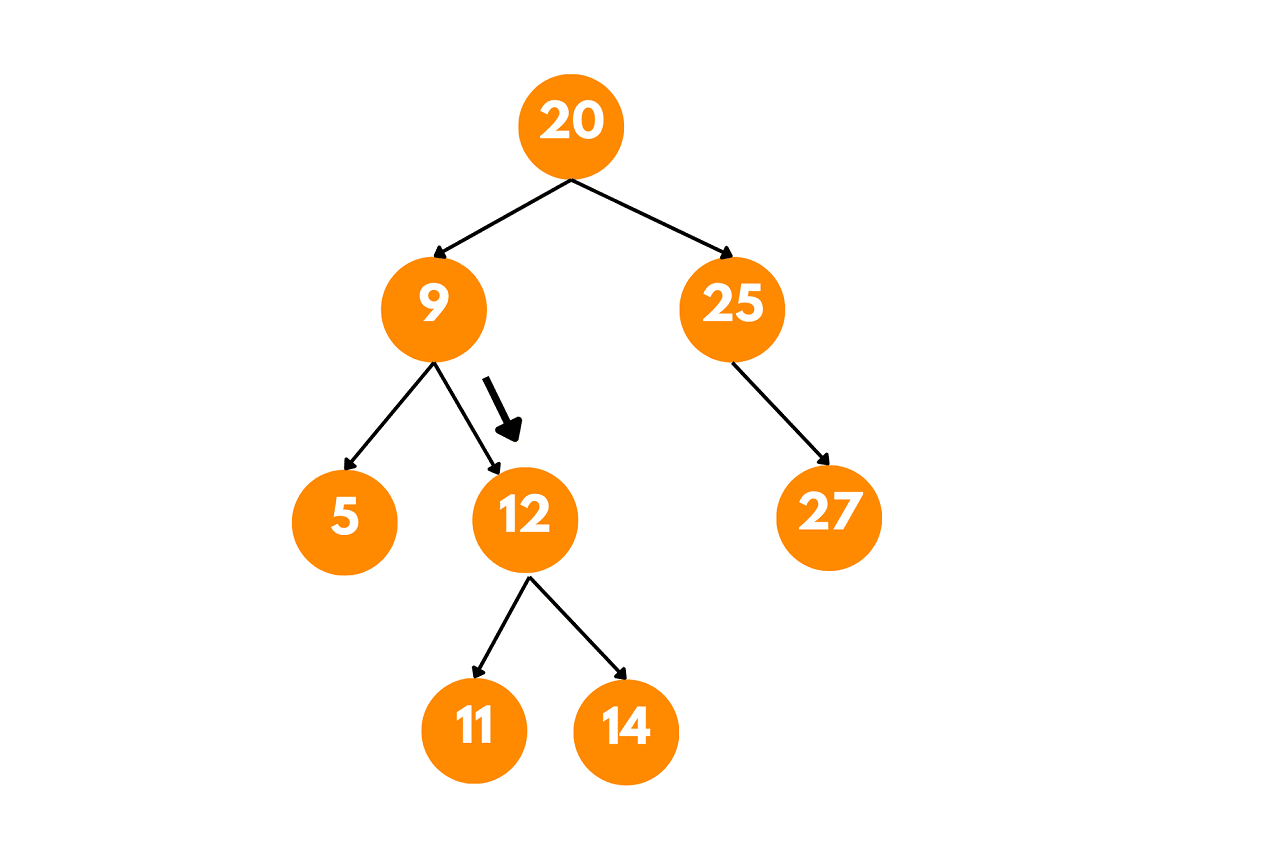
Now, we reach the node with value 12. Since we are looking for the inorder successor, we need to consider two cases:
-
If the node has a right subtree: In this case, we find the leftmost (minimum) value in the right subtree. In our example, the node with value 12 has a right subtree.
So, we move to the right subtree of the node with value 12, which leads us to the node with value 14. However, 14 does not have a left subtree, so it is the leftmost node in the right subtree of 12. Therefore, 14 is the inorder successor of 12.
-
If the node does not have a right subtree: In this case, there is no node with a value greater than the current node in the BST. We need to backtrack to the nearest ancestor for which the given node is in the left subtree. The parent node of the current node is the inorder successor.
In our example, if we were to find the inorder successor of the node with value 9, we would move up to its parent, which is the root node 20. So, the inorder successor of 9 is 20.
In conclusion, the inorder successor of the node with value 12 in the given BST is 14.
To find the inorder successor of a node in a BST, we can employ various techniques based on the structure and properties of the tree. Here are two common approaches.
Recursive Approach of Inorder Successor of a BST
Here is the step-by-step algorithm to find the inorder successor of a Binary Search Tree
- Perform an inorder traversal of the BST, keeping track of the previously visited node.
- When the desired node is found, check if it has the right subtree.
- If a right subtree exists, return the leftmost node in the right subtree.
- If there is no right subtree, return the previously visited node.
Here's a C++ code implementation of the recursive approach:
#include // Definition of a BST Node struct Node { int data; Node* left; Node* right; Node(int value) { data = value; left = nullptr; right = nullptr; } }; // Function to insert a new node in BST Node* insertNode(Node* root, int value) { if (root == nullptr) { return new Node(value); } if (value < root->data) { root->left = insertNode(root->left, value); } else { root->right = insertNode(root->right, value); } return root; } // Function to find the leftmost node (minimum value) in a BST Node* findMin(Node* node) { if (node->left == nullptr) { return node; } return findMin(node->left); } // Function to find the inorder successor of a node in BST Node* findInorderSuccessor(Node* root, Node* target) { if (root == nullptr || target == nullptr) { return nullptr; } if (target->right != nullptr) { // Case 1: If the target node has a right subtree, // the inorder successor is the leftmost node in the right subtree return findMin(target->right); } else { // Case 2: If the target node does not have a right subtree, // the inorder successor is the closest ancestor whose left subtree contains the target node Node* successor = nullptr; Node* current = root; while (current != nullptr) { if (target->data < current->data) { successor = current; current = current->left; } else if (target->data > current->data) { current = current->right; } else { break; // Found the target node } } return successor; } } // Function to display the inorder traversal of a BST void inorderTraversal(Node* root) { if (root == nullptr) { return; } inorderTraversal(root->left); std::cout << root->data << " "; inorderTraversal(root->right); } // Test the code int main() { Node* root = nullptr; // Insert nodes into the BST root = insertNode(root, 20); insertNode(root, 9); insertNode(root, 25); insertNode(root, 5); insertNode(root, 12); insertNode(root, 27); insertNode(root, 11); insertNode(root, 14); std::cout << "Inorder Traversal: "; inorderTraversal(root); std::cout << std::endl; // Find the inorder successor of a node Node* target = root->left->right; // Target node: 12 Node* successor = findInorderSuccessor(root, target); if (successor != nullptr) { std::cout << "Inorder Successor of " << target->data << ": " << successor->data << std::endl; } else { std::cout << "Inorder Successor of " << target->data << " not found." << std::endl; } return 0; }
Output:
Inorder Traversal: 5 9 11 12 14 20 25 27 Inorder Successor of 12: 14
In this code, we first define the structure for a BST node. Then, we implement the insertNode function to insert nodes into the BST. The findInorderSuccessor function uses an iterative approach to find the inorder successor.
Overall, the time complexity of the code depends on the specific operations performed on the BST, but it can range from O(log n) to O(n) depending on the tree's balance.
The space complexity of the code is O(n) in the worst-case scenario when the tree is skewed. In a balanced BST, the space complexity is O(log n) due to the recursive calls on the height of the tree.
Iterative Approach
Here is the step-by-step algorithm to find the inorder successor of BST using interaction:
- Start from the root and traverse the BST while maintaining a reference to the potential inorder successor.
- Compare the node's value with the given node:
- If the current node's value is greater, update the potential inorder successor and move to the left subtree.
- If the current node's value is smaller or equal, move to the right subtree.
- Repeat until reaching the desired node or a null reference.
- Return the potential inorder successor.
Get the code for the Iterative Approach of Inorder Successor:
#include using namespace std; // Definition of a BST Node struct Node { int data; Node* left; Node* right; Node(int value) { data = value; left = nullptr; right = nullptr; } }; // Function to insert a new node in BST Node* insertNode(Node* root, int value) { if (root == nullptr) { return new Node(value); } if (value < root->data) { root->left = insertNode(root->left, value); } else { root->right = insertNode(root->right, value); } return root; } // Function to find the leftmost node (minimum value) in a BST Node* findMin(Node* node) { if (node->left == nullptr) { return node; } return findMin(node->left); } // Function to find the inorder successor of a node in BST Node* findInorderSuccessor(Node* root, Node* target) { if (root == nullptr || target == nullptr) { return nullptr; } Node* successor = nullptr; while (root != nullptr) { if (target->data < root->data) { successor = root; root = root->left; } else if (target->data > root->data) { root = root->right; } else { if (root->right != nullptr) { // Case 1: If the target node has a right subtree, // the inorder successor is the leftmost node in the right subtree successor = findMin(root->right); } break; } } return successor; } // Test the code int main() { Node* root = nullptr; // Insert nodes into the BST root = insertNode(root, 20); insertNode(root, 9); insertNode(root, 25); insertNode(root, 5); insertNode(root, 12); insertNode(root, 27); insertNode(root, 11); insertNode(root, 14); // Find the inorder successor of a node Node* target = root->left->right; // Target node: 12 Node* successor = findInorderSuccessor(root, target); if (successor != nullptr) { cout << "Inorder Successor of " << target->data << ": " << successor->data << endl; } else { cout << "Inorder Successor of " << target->data << " not found." << endl; } return 0; }
Output:
Inorder Successor of 12: 14
In this code, we first define the structure for a BST node. Then, we implement the insertNode function to insert nodes into the BST. The findMin function is used to find the leftmost (minimum value) node in a BST. Finally, the findInorderSuccessor function uses an iterative approach to find the inorder successor of a given node in the BST.
The time complexity of the code depends on the specific operations performed on the BST, but it can range from O(log n) to O(n) depending on the tree's balance.
The overall space complexity of the code is O(n) in the worst-case scenario when the tree is skewed. In a balanced BST, the space complexity is O(h), where h is the height of the tree.
Conclusion
In conclusion, understanding the concept of the in-order successor in a binary search tree is fundamental to mastering tree traversal and manipulation. You can connect with our DSA Tutors online for more assistance or personal tutoring.








