In this article, we will study what is the minimum spanning tree and how to convert a graph into a minimum spanning tree using Prim’s Algorithm. We will learn the algorithm and python code for prim’s algorithm and an example for better understanding. Lastly, we will study the running time complexity and applications of prim's algorithm in real life. So, let’s get started!
What is a Minimum Spanning Tree?
As we all know, the graph which does not have edges pointing to any direction in a graph is called an undirected graph and the graph always has a path from a vertex to any other vertex. A spanning tree is a subgraph of the undirected connected graph where it includes all the nodes of the graph with the minimum possible number of edges. Remember, the subgraph should contain each and every node of the original graph. If any node is missed out then it is not a spanning tree and also, the spanning tree doesn’t contain cycles. If the graph has n number of nodes, then the total number of spanning trees created from a complete graph is equal to n^(n-2). In a spanning tree, the edges may or may not have weights associated with them. Therefore, the spanning tree in which the sum of edges is minimum as possible then that spanning tree is called the minimum spanning tree. One graph can have multiple spanning-tree but it can have only one unique minimum spanning tree. There are two different ways to find out the minimum spanning tree from the complete graph i.e Kruskal's algorithm and Prim’s algorithm. Let us study prim’s algorithm in detail below:
What is Prim’s Algorithm?
Prim’s algorithm is a minimum spanning tree algorithm which helps to find out the edges of the graph to form the tree including every node with the minimum sum of weights to form the minimum spanning tree. Prim’s algorithm starts with the single source node and later explore all the adjacent nodes of the source node with all the connecting edges. While we are exploring the graphs, we will choose the edges with the minimum weight and those which cannot cause the cycles in the graph.
Prim's Algorithm for Minimum Spanning Tree
Prim's algorithm basically follows the greedy algorithm approach to find the optimal solution. To find the minimum spanning tree using prim's algorithm, we will choose a source node and keep adding the edges with the lowest weight.
The algorithm is as given below:
- Initialize the algorithm by choosing the source vertex
- Find the minimum weight edge connected to the source node and another node and add it to the tree
- Keep repeating this process until we find the minimum spanning tree
Pseudocode
T = ∅; M = { 1 }; while (M ≠ N) let (m, n) be the lowest cost edge such that m ∈ M and n ∈ N - M; T = T ∪ {(m, n)} M = M ∪ {n}
Here we create two sets of nodes i.e M and M-N. M set contains the list of nodes that have been visited and the M-N set contains the nodes that haven’t been visited. Later, we will move each node from M to M-N after each step by connecting the least weight edge.
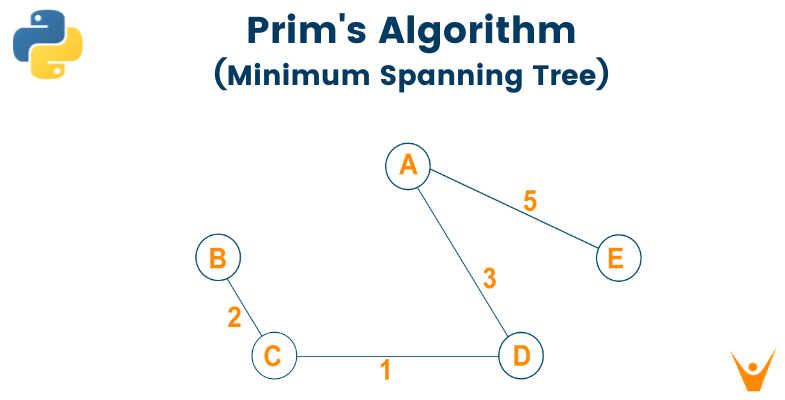
Example
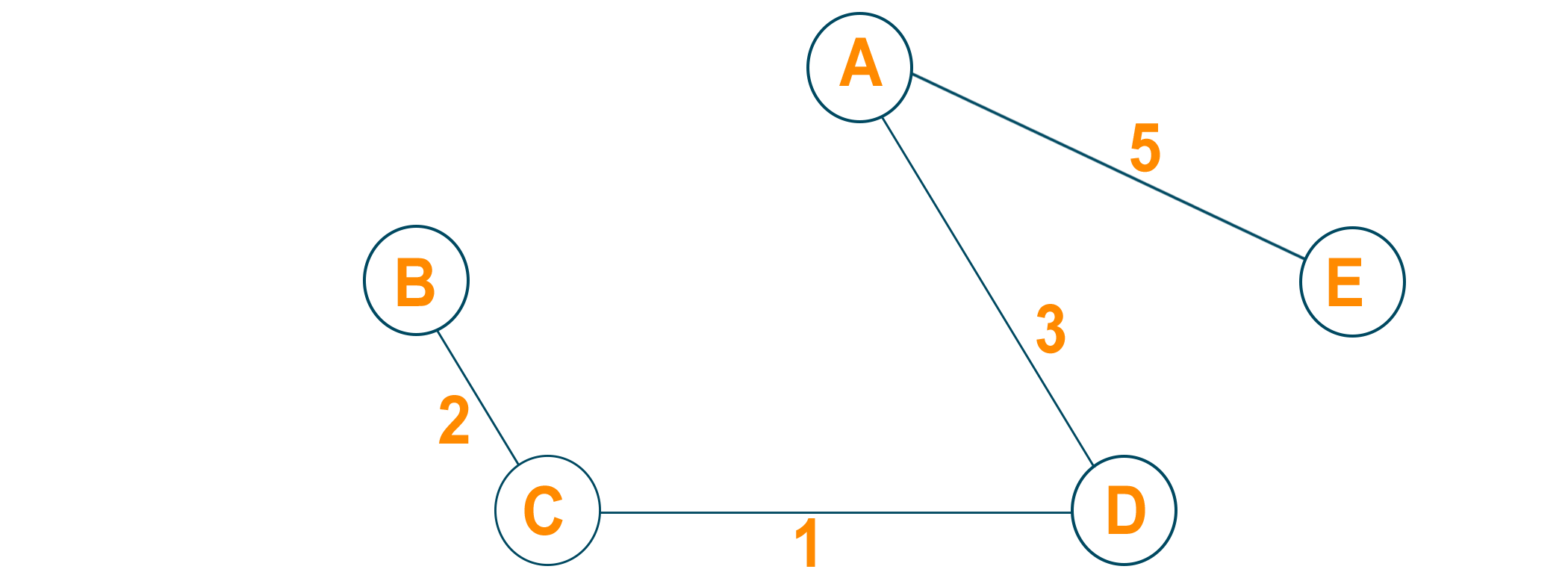
Let us consider the below-weighted graph
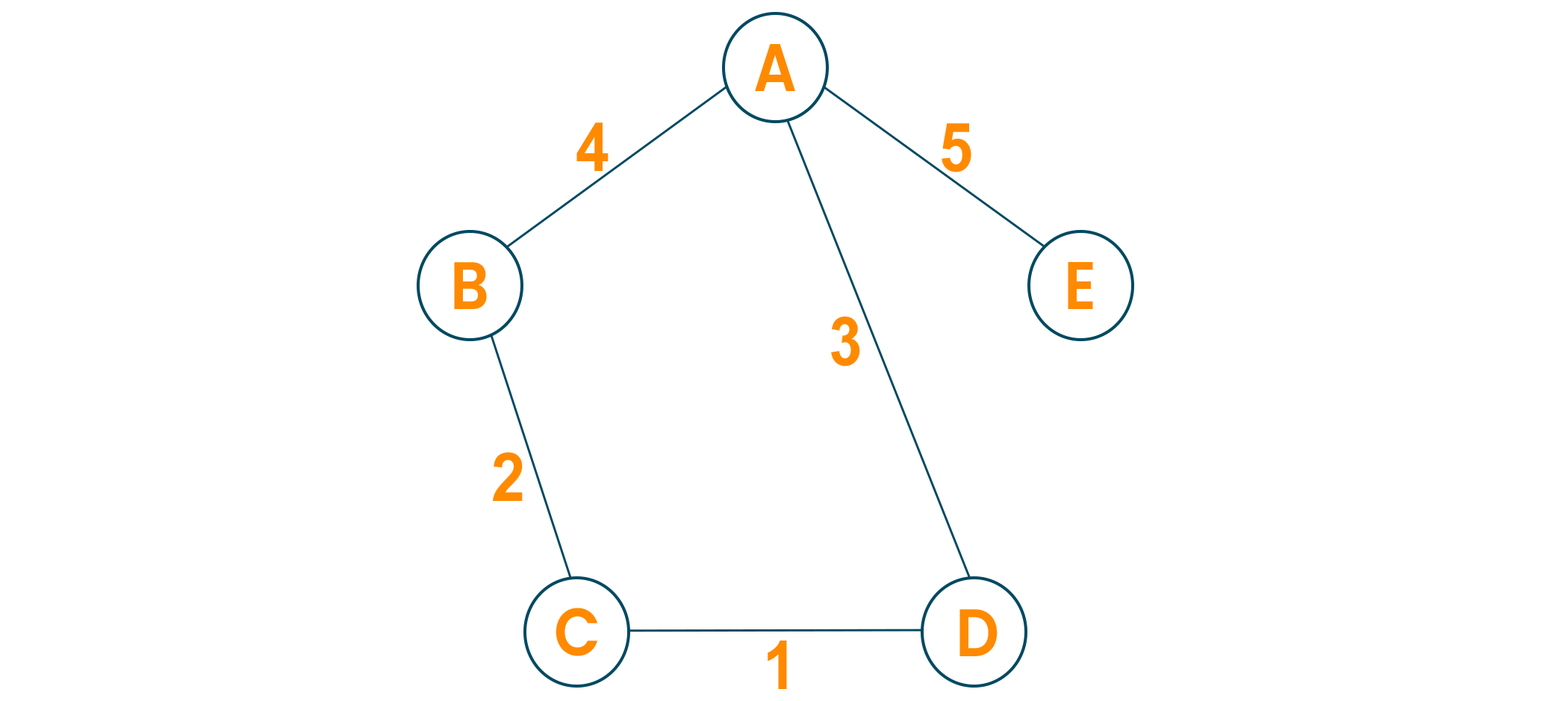
Later we will consider the source vertex to initialize the algorithm

Now, we will choose the shortest weight edge from the source vertex and add it to finding the spanning tree.
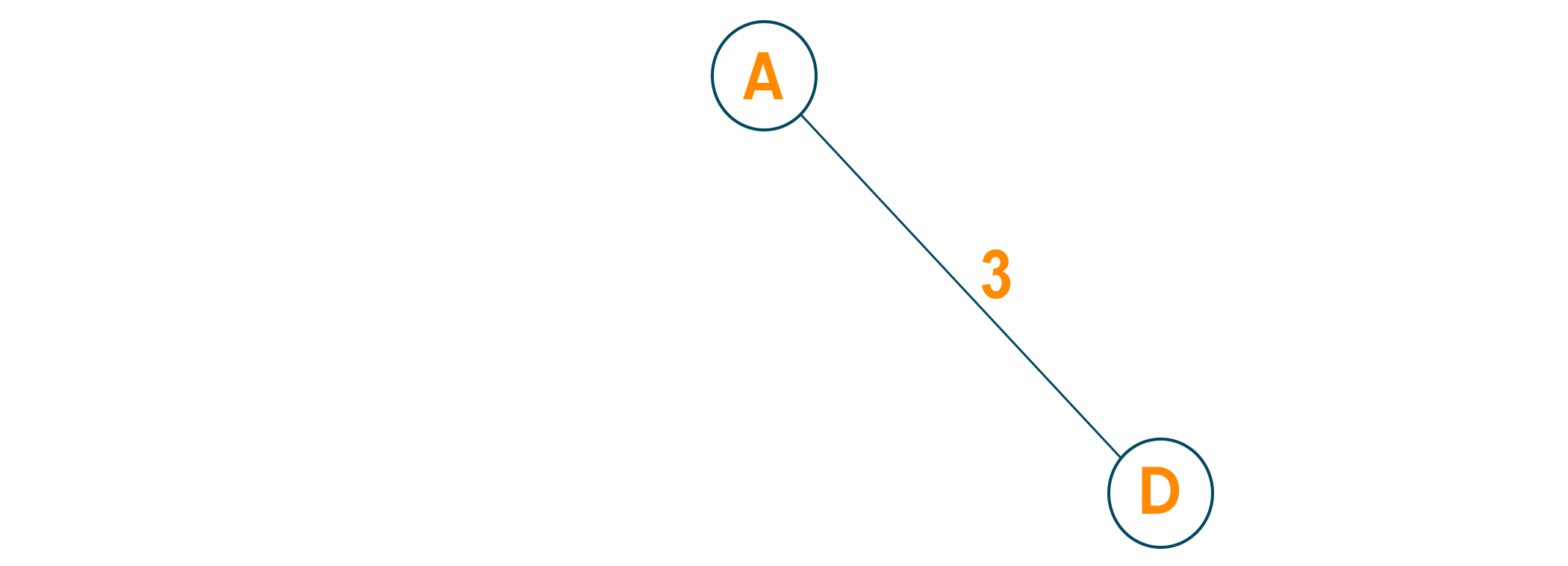
Then, choose the next nearest node connected with the minimum edge and add it to the solution. If there are multiple choices then choose anyone.
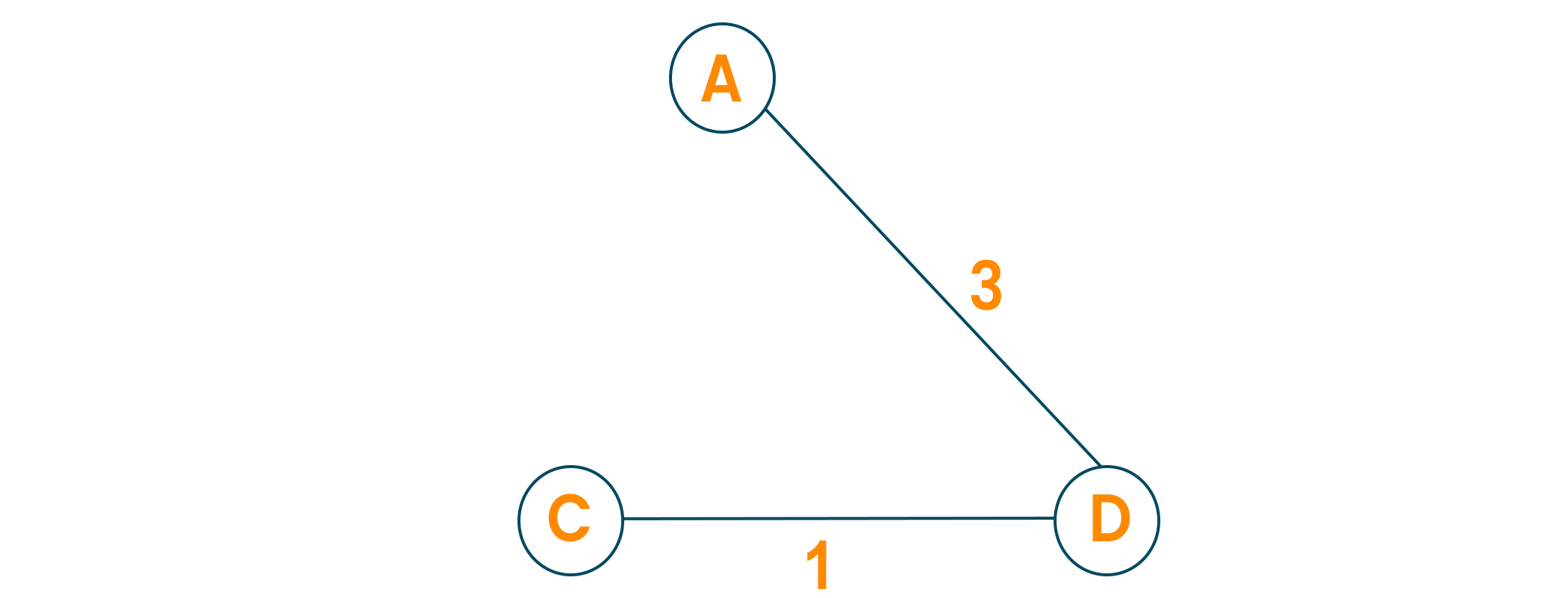
Continue the steps until all nodes are included and we find the minimum spanning tree.
Python Code for Prim’s Algorithm
# Prim's Algorithm in Python INF = 9999999 # number of vertices in graph N = 5 #creating graph by adjacency matrix method G = [[0, 19, 5, 0, 0], [19, 0, 5, 9, 2], [5, 5, 0, 1, 6], [0, 9, 1, 0, 1], [0, 2, 6, 1, 0]] selected_node = [0, 0, 0, 0, 0] no_edge = 0 selected_node[0] = True # printing for edge and weight print("Edge : Weight\n") while (no_edge < N - 1): minimum = INF a = 0 b = 0 for m in range(N): if selected_node[m]: for n in range(N): if ((not selected_node[n]) and G[m][n]): # not in selected and there is an edge if minimum > G[m][n]: minimum = G[m][n] a = m b = n print(str(a) + "-" + str(b) + ":" + str(G[a][b])) selected_node[b] = True no_edge += 1
Time Complexity:
The running time for prim’s algorithm is O(VlogV + ElogV) which is equal to O(ElogV) because every insertion of a node in the solution takes logarithmic time. Here, E is the number of edges and V is the number of vertices/nodes. However, we can improve the running time complexity to O(E + logV) of prim’s algorithm using Fibonacci Heaps.
Applications
- Prim’s algorithm is used in network design
- It is used in network cycles and rail tracks connecting all the cities
- Prim’s algorithm is used in laying cables of electrical wiring
- Prim’s algorithm is used in irrigation channels and placing microwave towers
- It is used in cluster analysis
- Prim’s algorithm is used in gaming development and cognitive science
- Pathfinding algorithms in artificial intelligence and traveling salesman problems make use of prim’s algorithm.
Conclusion
As we studied, the minimum spanning tree has its own importance in the real world, it is important to learn the prim’s algorithm which leads us to find the solution to many problems. When it comes to finding the minimum spanning tree for the dense graphs, prim’s algorithm is the first choice.