Dijkstra's Algorithm in C++ | Shortest Path Algorithm

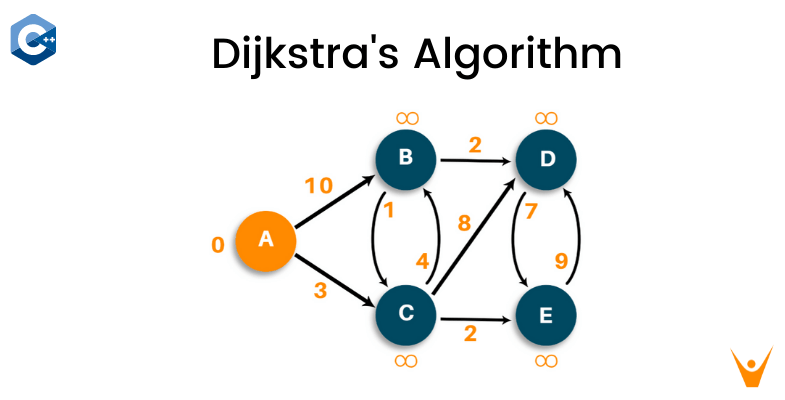
In this article, we will study what is the graph and what is Dijkstra's algorithm. Further, we will study the example of Dijkstra's algorithm and its c++ code along with its corresponding output. We will also further study the practical application of this algorithm in the real world. So let's get started!

What is Graph?

The graph is a non-linear data structure that involves nodes and edges. The nodes are the vertices and edges are the lines that connect the two nodes in the graph. Therefore, the graph can be defined as a set of vertices and a set of edges that connect the nodes. If we consider Facebook as a graph then the collection of people on Facebook is considered as nodes and the connection between them can be considered as edges. Therefore, graphs are the data structures used to display the "connection" between the pairs of elements. The below image shows the graphical representation of the graph.

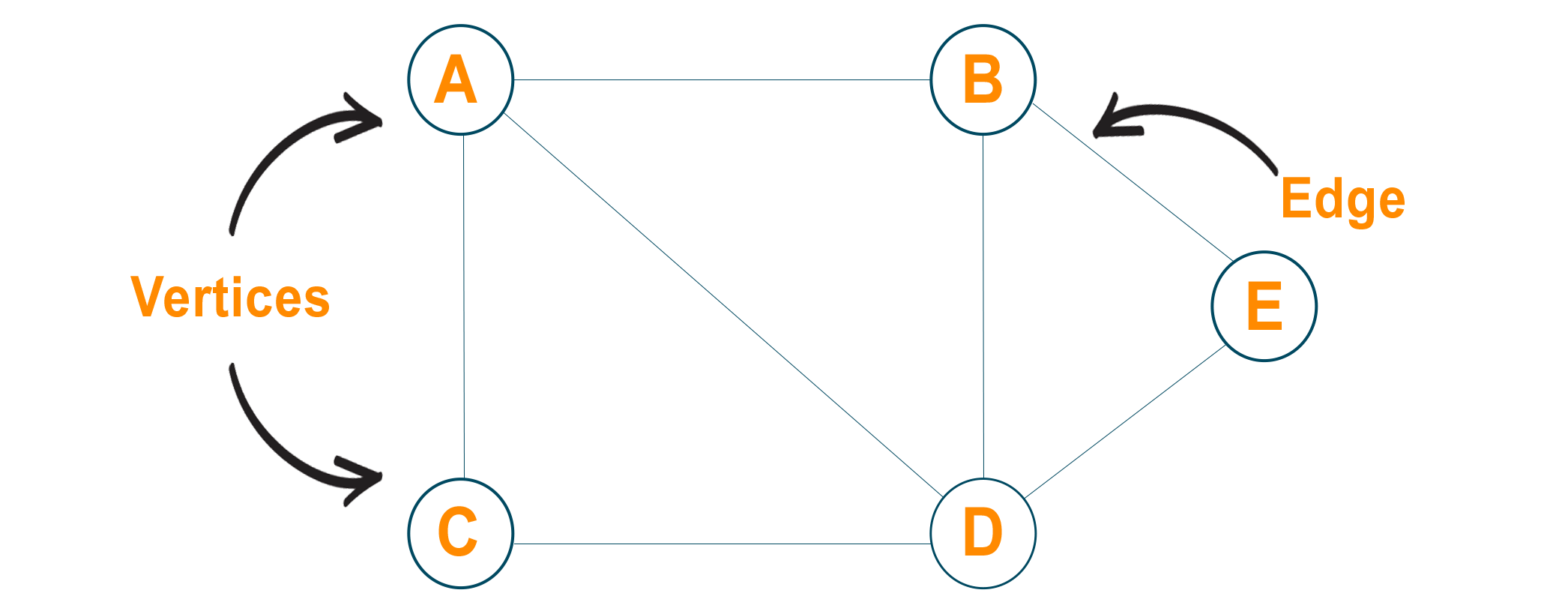
Generally, there are two types of graph possible: 

1. Undirected Graph: Using an Undirected graph, for every pair of connected nodes, you can go from one node to another in both directions.
2. Directed Graph: You can only go from one node to another in a specific direction for every pair of connected nodes using the directed graph. You can make use of arrows as an edge connecting two nodes. 
   Moreover, a weighted graph is a graph that consists of edges with some specific "weight" or "cost." The weight of the edge can represent time, distance, or anything that models the "connection" between pair of nodes.

What is Dijkstra’s Algorithm?

Dijkstra’s algorithm is also known as the shortest path algorithm. It is an algorithm used to find the shortest path between nodes of the graph. The algorithm creates the tree of the shortest paths from the starting source vertex from all other points in the graph. It differs from the minimum spanning tree as the shortest distance between two vertices may not be included in all the vertices of the graph. The algorithm works by building a set of nodes that have a minimum distance from the source. Here, Dijkstra's algorithm uses a greedy approach to solve the problem and find the best solution.

When Does Dijkstra's Algorithm Fail

Dijkstra's algorithm only works with the graph that possesses positive weights. While running an algorithm, the weights of the edges have to be added to find the shortest path between the nodes. If there is negative weight in the graph, then the algorithm will fail to work. Remember that once you mark the node as "visited," the current path to the node is the shortest path to reach that node. Therefore, if you have negative weights, it can alter this step if the total weight is decreased.

Moreover, while understanding Dijkstra's algorithm, the question arises that whether it is BFS or DFS? Well, it is neither. Dijkstra's algorithm is a priority first algorithm. However, between BFS and DFS algorithms, the priority will be more to BFS rather than DFS. Basically, you can find some essential structure of BFS inside Dijkstra's algorithm, but honestly, it is much more than the BFS algorithm.

Algorithm for Dijkstra’s in C++

To know how Dijkstra's algorithm works behind the scene, look at the below steps to understand it in detail:

1. First of all, we will mark all vertex as unvisited vertex
2. Then, we will mark the source vertex as 0 and all other vertices as infinity
3. Consider source vertex as current vertex
4. Calculate the path length of all the neighboring vertex from the current vertex by adding the weight of the edge in the current vertex
5. Now, if the new path length is smaller than the previous path length then replace it otherwise ignore it
6. Mark the current vertex as visited after visiting the neighbor vertex of the current vertex
7. Select the vertex with the smallest path length as the new current vertex and go back to step 4.
8. Repeat this process until all the vertex are marked as visited.

Once we go through the algorithm, we can backtrack the source vertex and find our shortest path.

Pseudocode of Dijkstra’s Algorithm in C++

function dijkstra(G, S)
    for each vertex V in G
        dist[V] <- infinite
        prev[V] <- NULL
        If V != S, add V to Priority Queue Q
    dist[S] <- 0
    
    while Q IS NOT EMPTY
        U <- Extract MIN from Q
        for each unvisited neighbour V of U
            temperoryDist <- dist[U] + edgeWeight(U, V)
            if temperoryDist < dist[V]
                dist[V] <- temperoryDist
                prev[V] <- U
    return dist[], prev[]

Example

Let us consider the below example to understand the algorithm. Here we are given a weighted graph, and we will choose vertex 'A' as the source vertex of the graph. 

As the algorithm generates the shortest path from the source vertex to every other vertex, we will set the distance of the source vertex to itself as '0'. The distance from the source vertex to all other vertex is not determined yet, and therefore, we will represent it using infinity. 

For now, the list of unvisited nodes will be: {B, C, D, E}

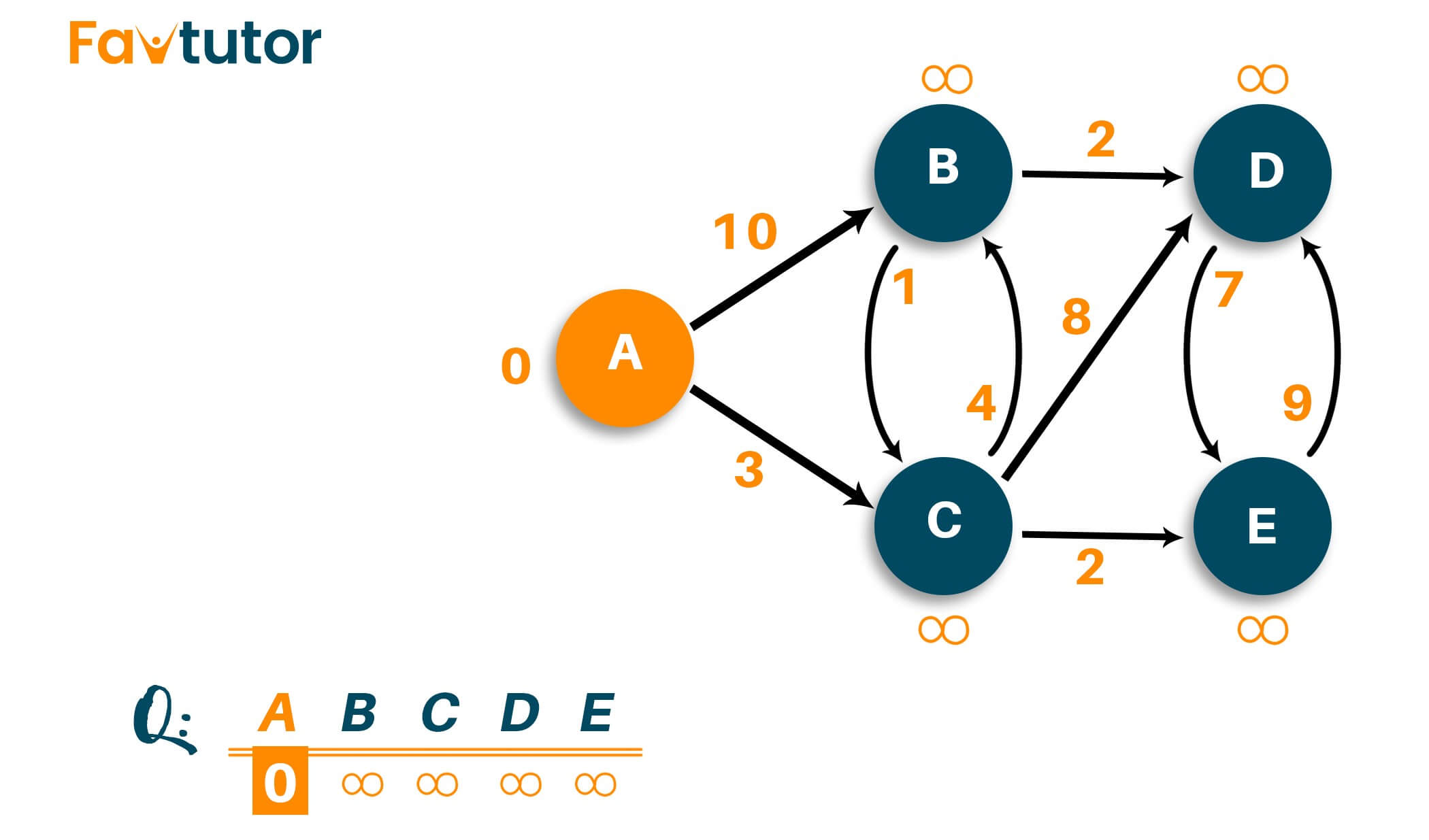
Here, we will start checking the distance from node 'A' to its adjacent vertex. You can see the adjacent vertexes are 'B' and 'C' with weights '10' and '3', respectively. Remember that you don't have to add the two vertexes to the shortest path immediately.

Firstly, we will update the distance from infinity to given weights. Then we have to select the node closest to the source node depending on the updated weights. Mark it as visited and add it to the path. 

As shown below, we update vertex B from infinity to 10 and vertex C from infinity to 3.

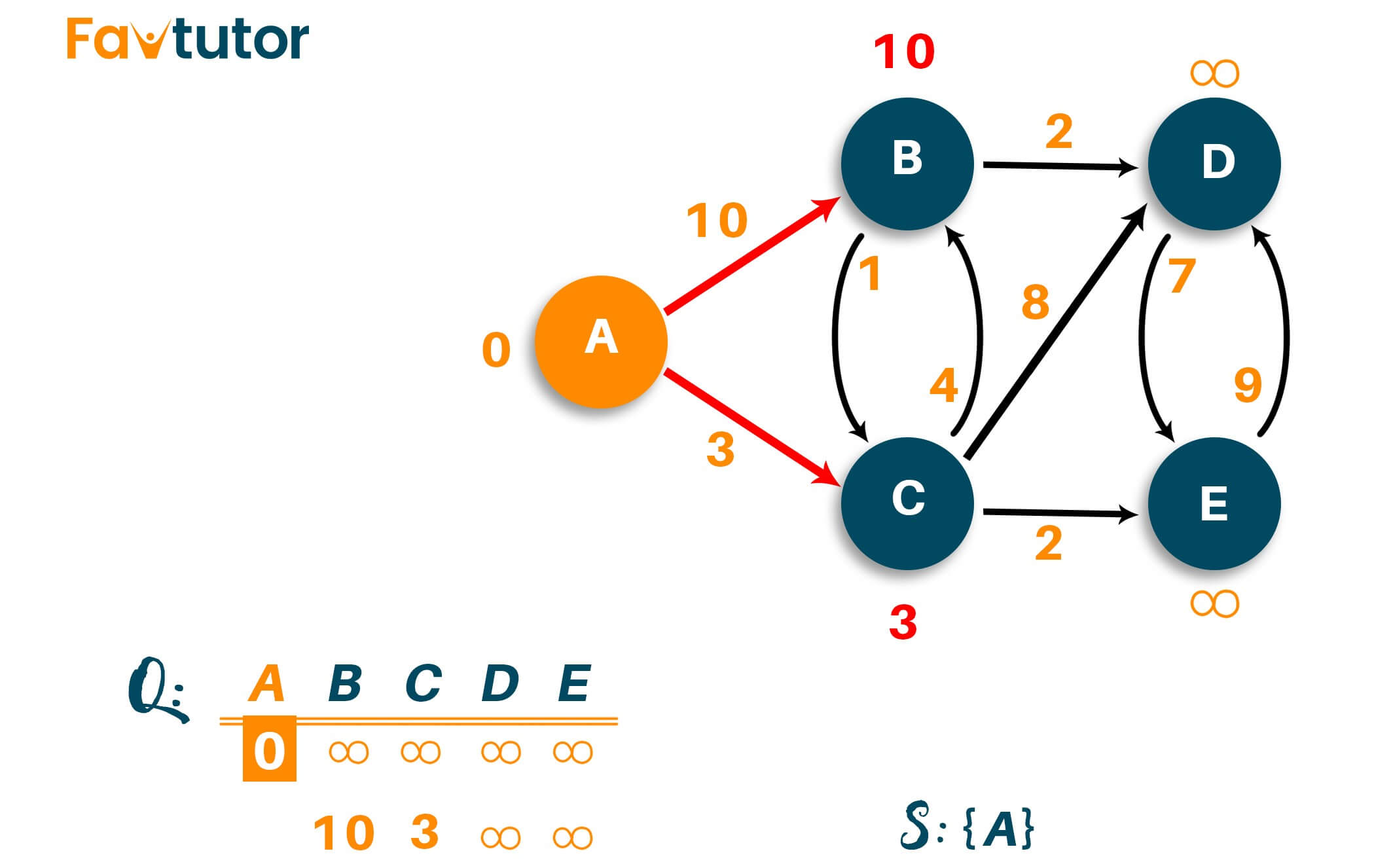
Now select the vertex with the smaller path length as visited vertex and put it in the answer. Therefore, the list of unvisited nodes is {B, D, E}

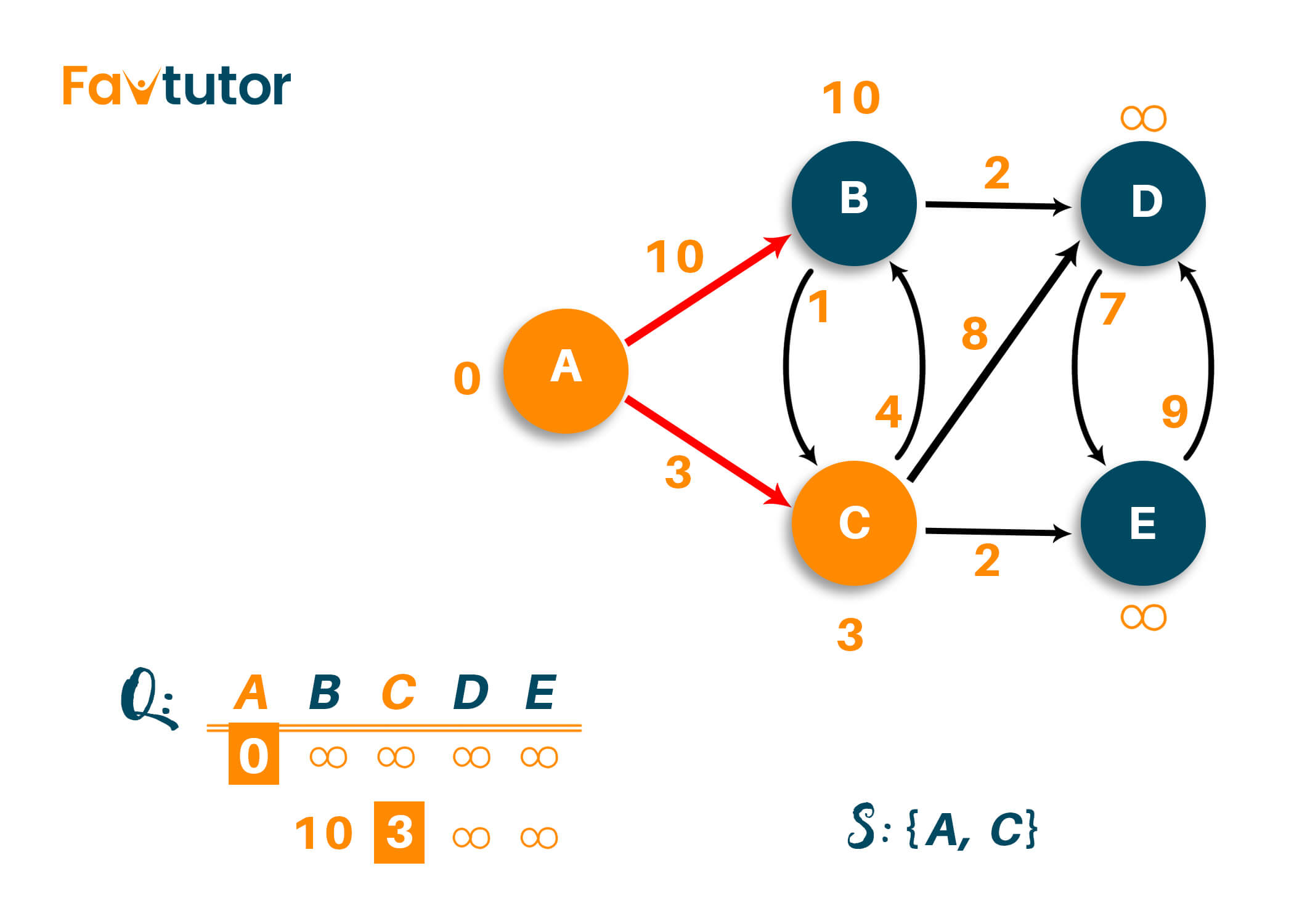
Now, we have to analyze the new adjacent vertex to find the shortest path. So we will visit the neighboring nodes of the visited vertex and update the path lengths as required. Here, we have B, D, and E as adjacent vertex to node 'A' and node 'C.' Therefore, we will update the path of all three vertexes from infinity to their respective weights as shown in the image below.

Note that node 'B' is directly connected adjacent to node 'A,' hence, node 'B' weight will be the same as displayed. But for Node 'D' and node 'E,' the path is calculated via node 'C,' and hence the weight of that vertex will be 11 and 5 because we add the weight of the edges from path A->C->D and A->C->E respectively.

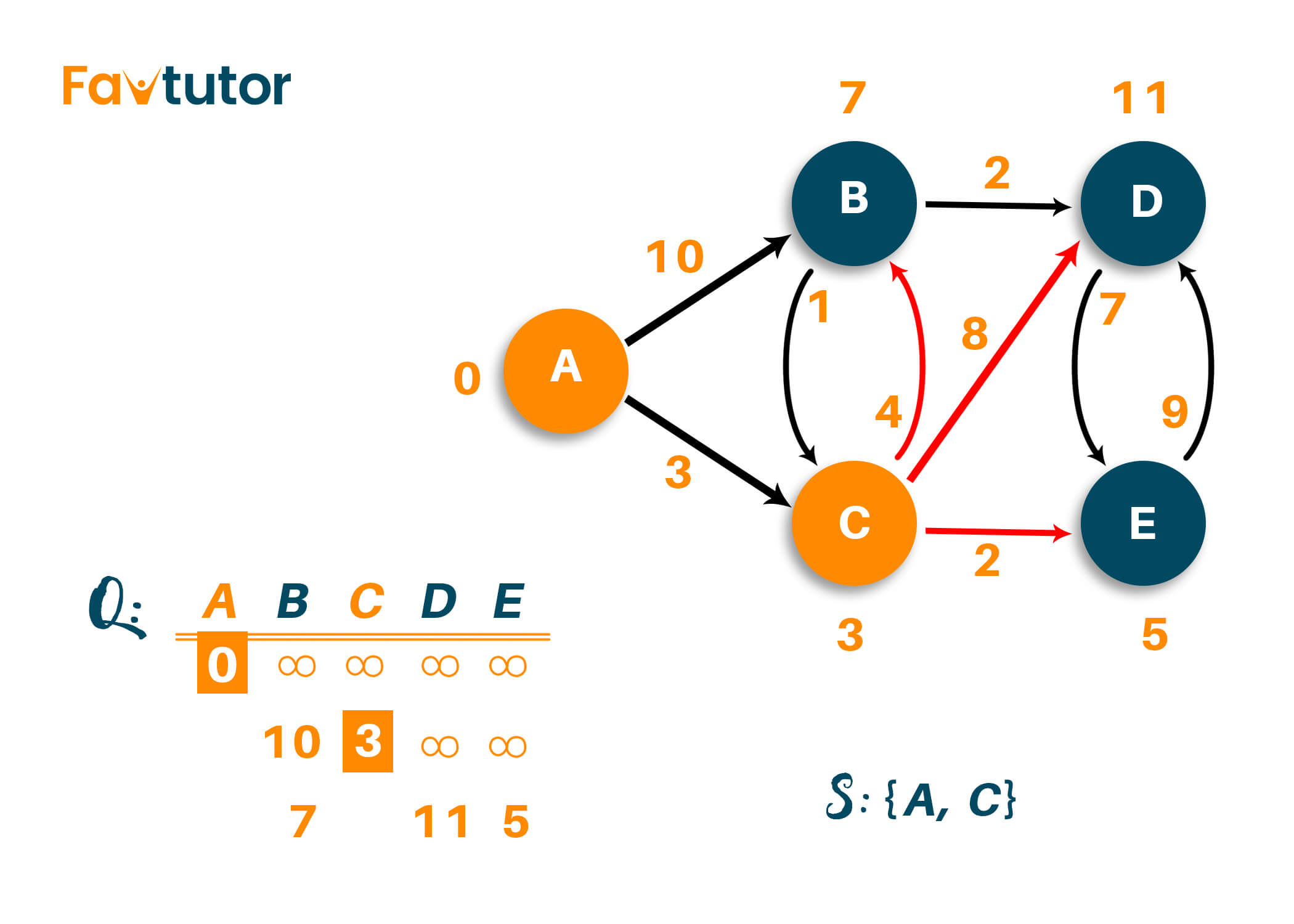
Now, choosing the shortest path from the above table results in choosing the node 'E' with the shortest distance of 5 from the source vertex. And hence the list of unvisited nodes is {B, D}

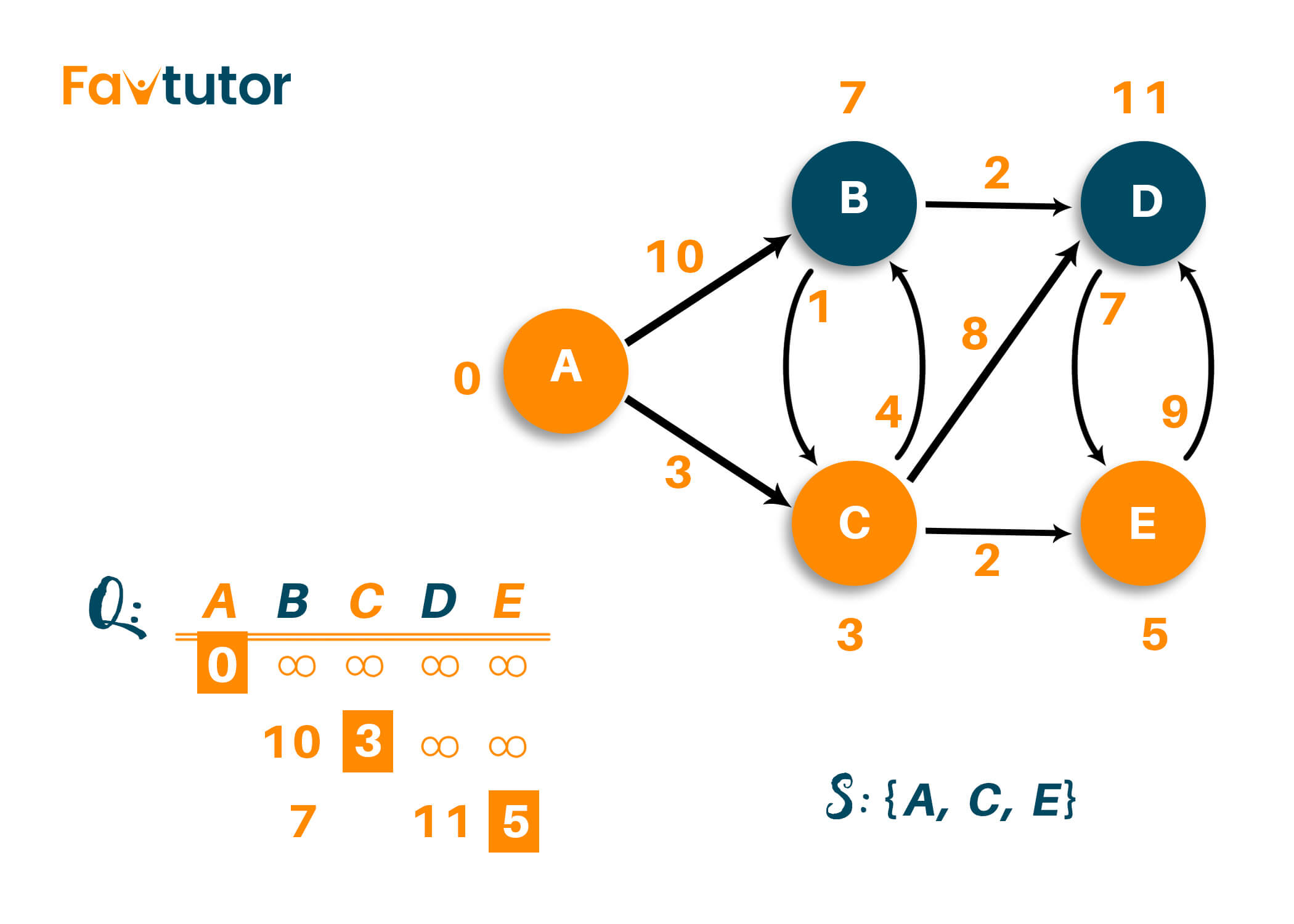
Repeat the process until all vertices have been visited. Here, vertex 'B' and vertex 'D' are both considered adjacent vertex, and the shortest distance of both the vertex from the source node does not change, as shown in the figure below.

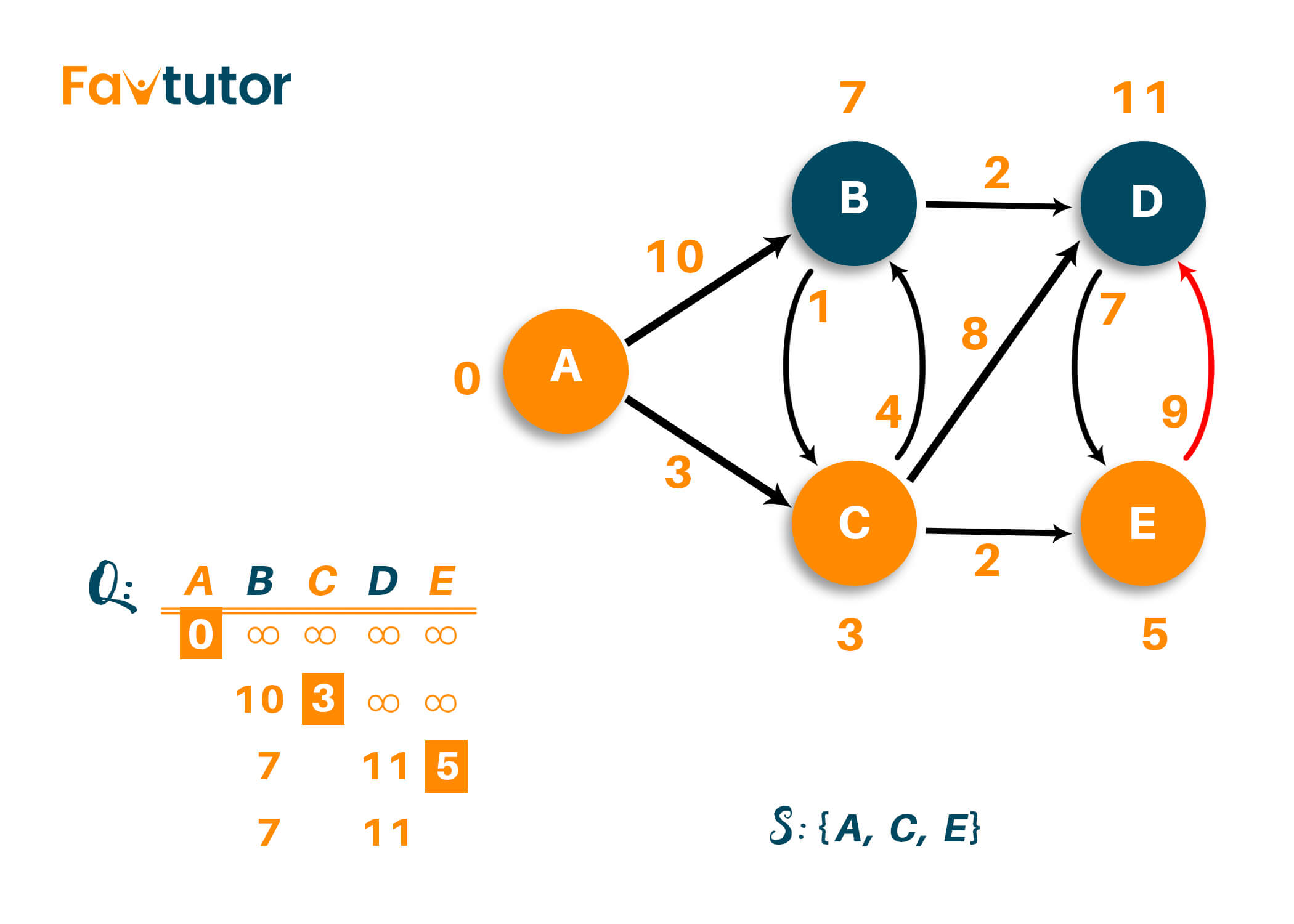
Therefore, the weight of vertex 'B' is minimum compared to vertex 'D,' so we will mark it as a visited node and add it to the path. The list of the unvisited nodes will be {D}

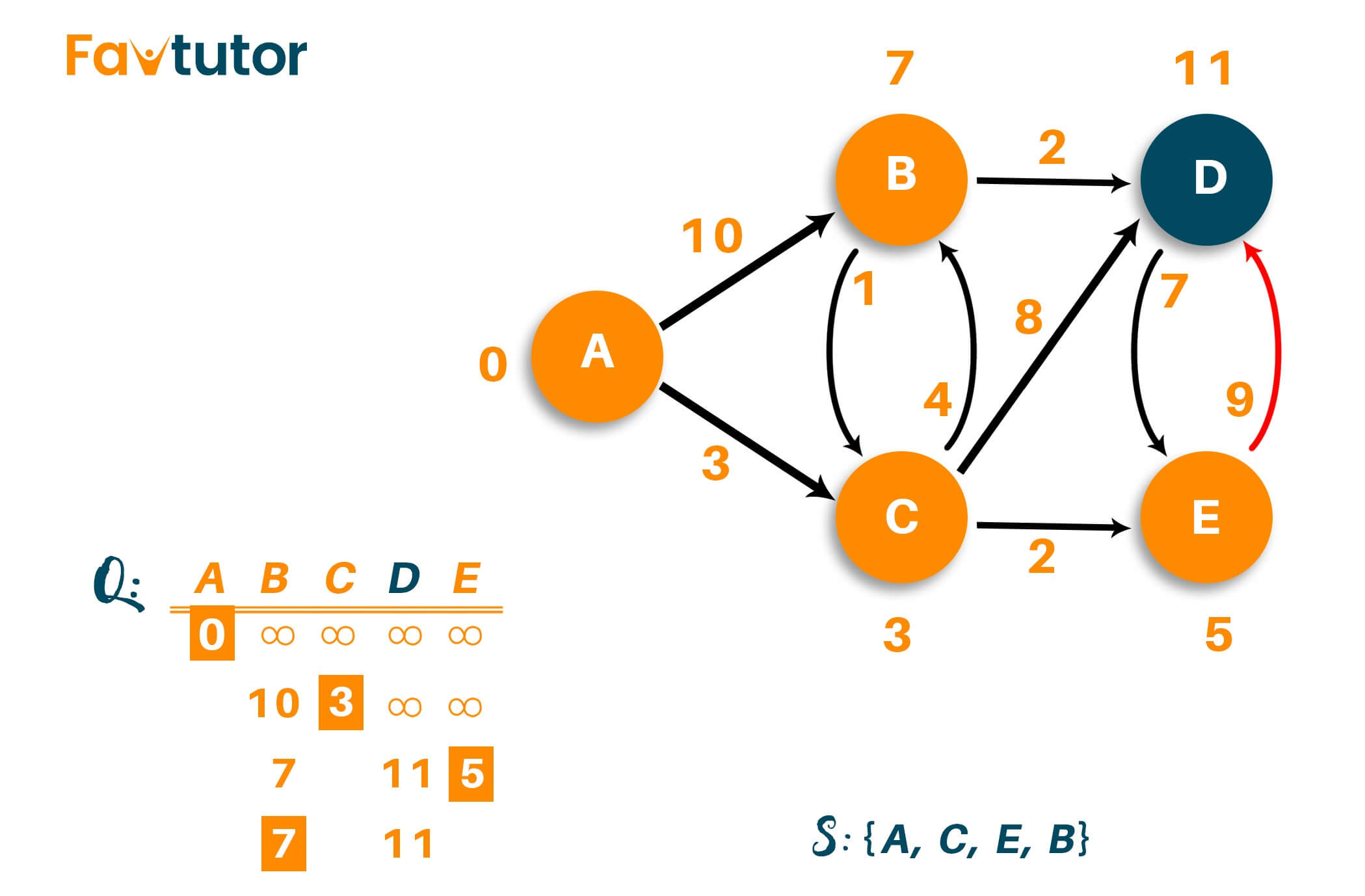
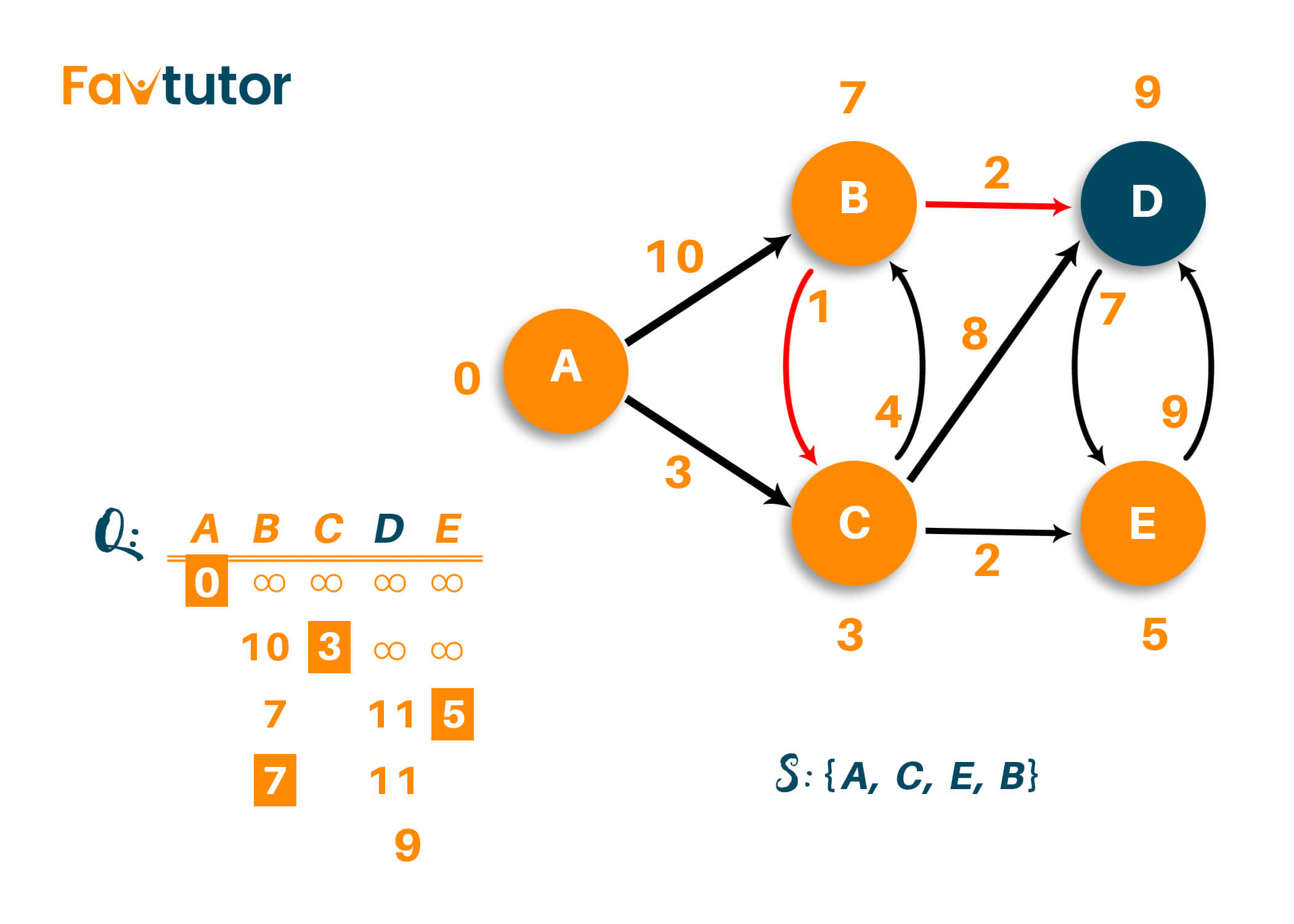
After visiting vertex 'B,' we are left with visiting vertex 'D.' If you carefully notice, the distance from source vertex to vertex 'D' can be modified from the previous one, i.e., instead of visiting vertex 'D' directly via vertex 'C,' we can visit it via vertex 'B' with the total distance of 9. That is because we add the weight of the edges like A->C->B->D (3+4+2=9) as shown below.

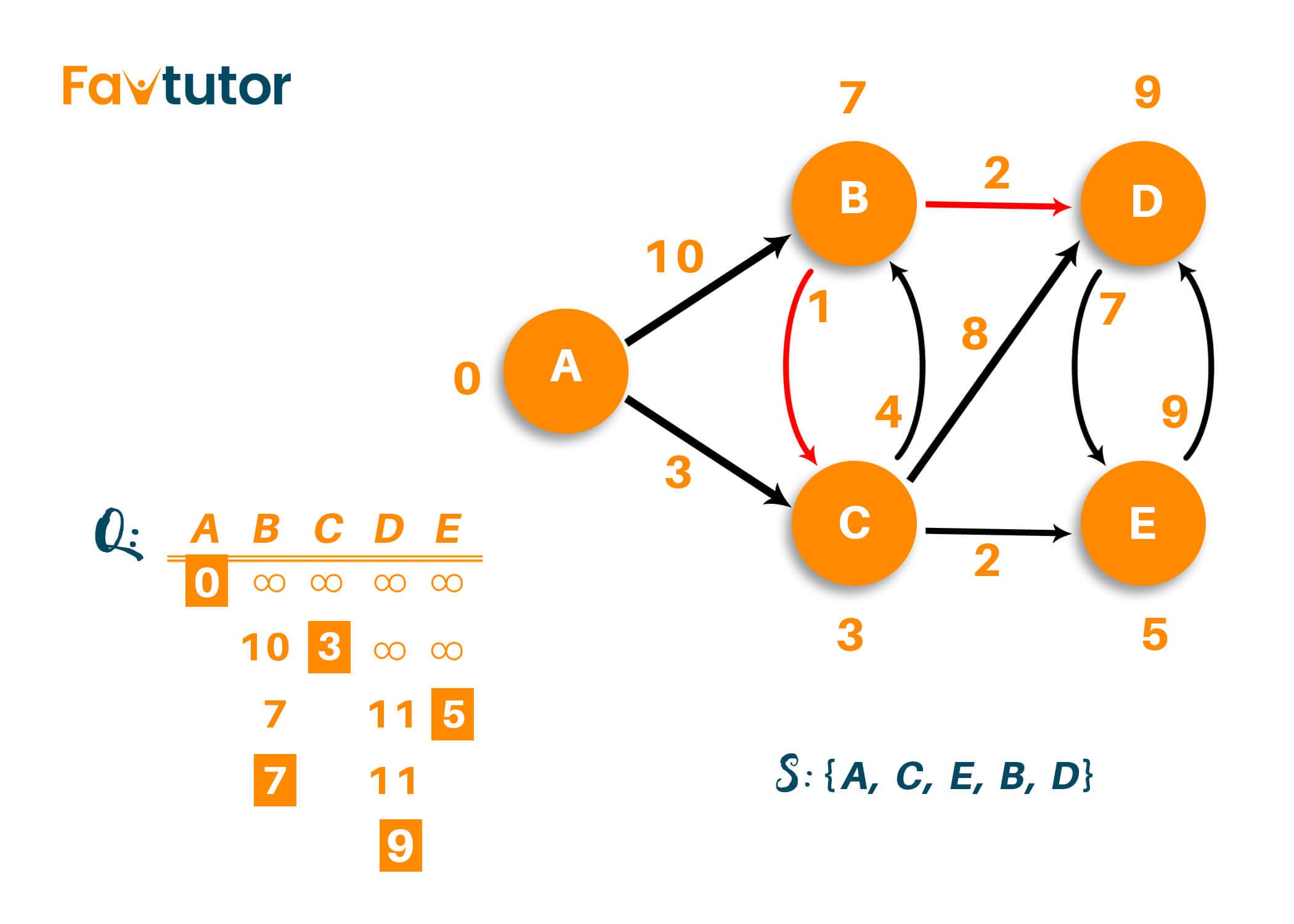
Therefore, the final output of the algorithm will be {A, C, E, B, D}

C++ code for Dijkstra’s Algorithm

#include
#include
using namespace std;

int miniDist(int distance[], bool Tset[]) // finding minimum distance
{
    int minimum=INT_MAX,ind;
              
    for(int k=0;k<6;k++) 
    {
        if(Tset[k]==false && distance[k]<=minimum)      
        {
            minimum=distance[k];
            ind=k;
        }
    }
    return ind;
}

void DijkstraAlgo(int graph[6][6],int src) // adjacency matrix 
{
    int distance[6]; // // array to calculate the minimum distance for each node                             
    bool Tset[6];// boolean array to mark visited and unvisited for each node
    
     
    for(int k = 0; k<6; k++)
    {
        distance[k] = INT_MAX;
        Tset[k] = false;    
    }
    
    distance[src] = 0;   // Source vertex distance is set 0               
    
    for(int k = 0; k<6; k++)                           
    {
        int m=miniDist(distance,Tset); 
        Tset[m]=true;
        for(int k = 0; k<6; k++)                  
        {
            // updating the distance of neighbouring vertex
            if(!Tset[k] && graph[m][k] && distance[m]!=INT_MAX && distance[m]+graph[m][k]<distance[k])
                distance[k]=distance[m]+graph[m][k];
        }
    }
    cout<<"Vertex\t\tDistance from source vertex"<<endl;
    for(int k = 0; k<6; k++)                      
    { 
        char str=65+k; 
        cout<<str<<"\t\t\t"<<distance[k]<<endl;
    }
}

int main()
{
    int graph[6][6]={
        {0, 1, 2, 0, 0, 0},
        {1, 0, 0, 5, 1, 0},
        {2, 0, 0, 2, 3, 0},
        {0, 5, 2, 0, 2, 2},
        {0, 1, 3, 2, 0, 1},
        {0, 0, 0, 2, 1, 0}};
    DijkstraAlgo(graph,0);
    return 0;                           
}

Output

Vertex         Distance from source

A                     0

B                     1

C                     2

D                     4

E                     2

F                     3

Time Complexity

The time complexity of Dijkstra's algorithm is O(V^2), where V is the number of vertices in the graph. However, if the input graph is represented using an adjacency list (method of representation of graph), then the time complexity can be reduced to O(E log V) using a binary heap.

The space complexity of Dijkstra's algorithm is O(V), where V is the total number of vertices of the graph. This is because we have to store all these vertices in the list as an output.

Applications

1. Dijkstra’s algorithm is used as a routing protocol required by the routers to update their forwarding table.
2. It is used to find the shortest distance between two locations along the path on google maps.
3. It is used in telephone networking to find the shortest path for finding the nearest switching station for transmission.
4. Dijkstra’s algorithm is used to find the shortest path between users measured through handshakes or connections among them.
5. Dijkstra’s algorithm is used to minimize the number of hops in computer networks.

Conclusion

Graphs are used as a connection between objects, people, or entities, and Dijkstra's algorithm will help you find the shortest distance between two points in a graph. As Dijkstra's algorithm has its own importance in the real world, it is most recommended to learn and understand it in detail.