Find Distance between Two Nodes of a Binary Tree (with code)

In computer science and data structures, a binary tree is a fundamental data structure that consists of nodes connected by edges. One common task when working with binary trees is determining how far are two nodes from each other. In this article, we will explore different approaches to calculating the distance between two nodes in a binary tree.

Distance between Two Nodes in Binary Tree

First, let's revise some basics of a binary tree. It is a hierarchical structure that consists of nodes connected by edges. Each node in a binary tree contains a value and can have at most two children: a left child and a right child.

The left child represents a node that is less than or equal to the current node's value, while the right child represents a node that is greater than the current node's value. The children of a node can themselves be binary trees, forming sub-trees of the overall structure.

In the above image, there is a binary tree with a root node as A.

So, let's now understand our problem. Here is the problem statement: "Given a root of a binary tree and two nodes. We need to find the distance between these 2 nodes. The distance here is the minimum number of edges to be traversed to reach from one node to another."

Let's understand the problem with an example:

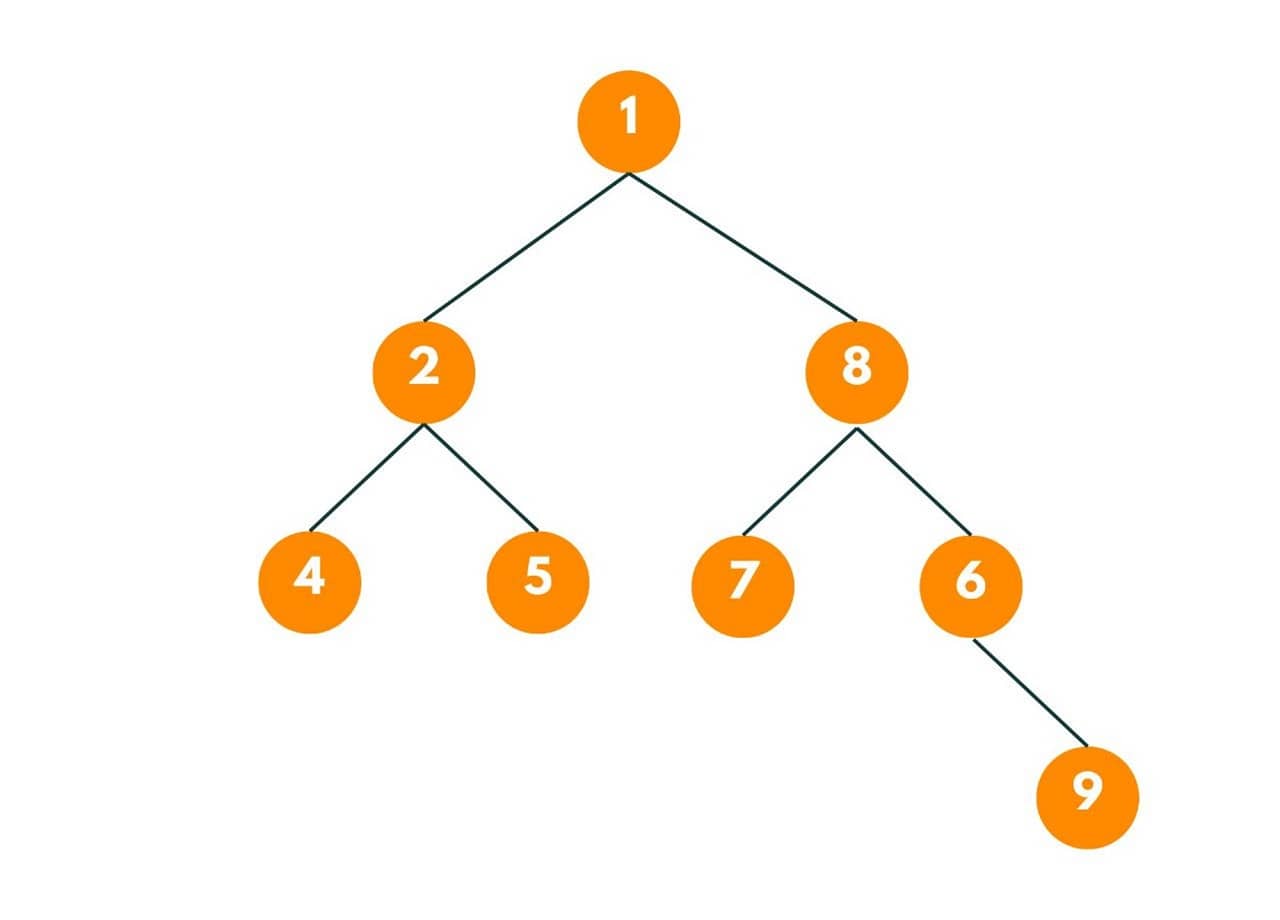
Here we need to find the distance between Node 7 and Node 8. Both nodes are 3 edges away from each other, so the answer is 3.

Algorithm to Find Distance between Two Nodes

Here is the step-by-step algorithm to find the distance between two nodes in a binary tree:

1. First, we will find the node-to-root path for both nodes in the form of two ArrayLists.
2. Then we begin from the last indices of both the ArrayLists.
3. If the value at both indices is the same, we decrease the pointers.
4. If both indices have different indices, we break and increase the pointer count by 1.
5. The pointers are pointing to the node where the path diverged for both the given nodes.
6. In the end, we return the answer by adding the length of ArrayList - pointer of both array lists.

Code for Implementation

Following is the simple programming code to find the distance between two nodes in a binary tree:

public static int distanceBetweenNodes(Node node, int d1, int d2) {
    // finding node to root path for both the nodes
    ArrayList< Integer> path1 = nodeToRootPath(node, d1);
    ArrayList< Integer> path2 = nodeToRootPath(node, d2);
    
    // setting the pointer to the last index of arraylists
    int pointer1 = path1.size() - 1;
    int pointer2 = path2.size() - 1;
    
    // finding the diverging node 
    while (pointer1 >= 0 && pointer2 >= 0 && path1.get(pointer1) == path2.get(pointer2)) {
      pointer1--;
      pointer2--;
    }
    pointer1++;
    pointer2++;
    
    //returning the edges
    return pointer1 + pointer2;
  }
  
  public static ArrayList< Integer> nodeToRootPath(Node node, int data) {
    if (node.data == data) {
      ArrayList< Integer> path = new ArrayList< >();
      path.add(node.data);
      return path;
    }

    for (Node child : node.children) {
      ArrayList< Integer> list = nodeToRootPath(child, data);
      if (list.size() > 0) {
        list.add(node.data);
        return list;
      }
    }

    return new ArrayList< >();
  }

Time & Space Complexity

The time complexity of the given code is O(N), where N is the number of nodes in the binary tree. This is because in the worst case, we may need to traverse the entire tree to find the node-to-root paths for both nodes.

The space complexity of the code is O(N), where N is the number of nodes in the binary tree. This is because we are using ArrayLists to store the node-to-root paths, and in the worst case, the paths can contain all the nodes in the tree. Therefore, the space required is proportional to the number of nodes in the tree.

Applications

This task is commonly used in many scenarios in the programming world. Here are some common applications:

• Network Routing: The distance between nodes in a binary tree can be utilized in network routing algorithms. For example, in a hierarchical routing scheme, where nodes are organized in a binary tree structure, the distance between nodes can help determine the shortest path or the most efficient route for transmitting data between two specific nodes.
• Tree Traversals: The distance between two nodes can be used to define the relative position of nodes during tree traversals. For example, in an in-order traversal, the distance between two nodes can help identify the order in which they appear in the traversal.
• Binary Tree Diameter: The distance between the two farthest nodes is known as the diameter of the binary tree. By finding the distance between every pair of nodes in the tree, we can determine the maximum distance and hence the diameter of the tree.

Conclusion

By understanding these approaches, you can efficiently determine the distance between two nodes in a binary tree and solve related problems in various applications.