Container With Most Water (With C++, Java and Python Code)

Product-based companies like Google, Amazon, and Microsoft have started hiring students for their problem-solving abilities rather than just programming skills. Be it online assessments, technical rounds, or interviews they are gradually refraining from asking questions directly. Questions that are a combination of daily activities and programming concepts like dynamic programming, recursion, etc are being asked quite frequently. One such question that is gaining popularity around the subject is Container with Most Water. Today, we'll be discussing this problem, its approach, and how you can devise its solution. So, let's get started!

Problem Statement

You are given an array 'height' having 'n' non-negative integers. 'n' vertical lines are drawn so that the ending points of the ith line are (I,0) and (i, height[I]). Your task is to find the two lines forming a container that contains the most water inside it. Return the amount of water inside them. 

Note: You cannot slant the container. 

Example:

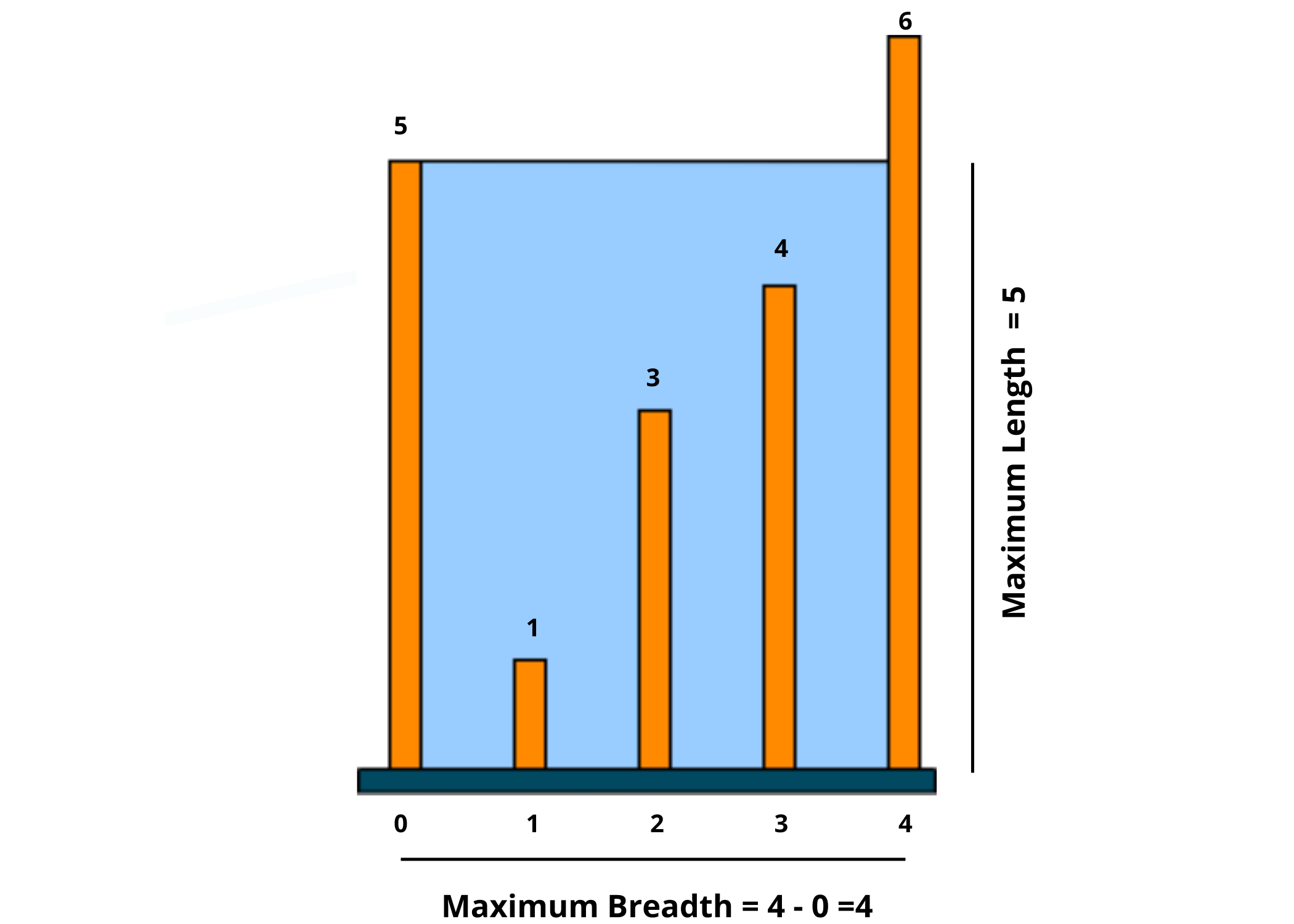
height=[5,1,3,4,6]

output=20

Let's take a look at the below image to understand how the output came out to be 20. 

Solutions

We have given 2 approaches to solve this question: the brute force method and the optimal solution. Although the first method works perfectly fine, its time complexity is longer than the second one. See for yourself!

Method 1: Brute Force Approach

The first naive approach that comes into our mind is called Brute Force Approach. It's not efficient yet we get the answer. The main idea here is to return the maximum area between the two lines, and observe that even though containers have a volume of water, you cannot express the answer as volume since we're in a 2D plane. Therefore, we need to find the area. 

Now, what determines the area? Its length and breadth. Hence, here we'll check each element pairing with the next element in the loop and calculate the area between them. If the area is larger than the previous one, we'll update it. Finally, the answer will be displayed as the output.

Algorithm:

Create a nested loop with the elements specified below and a variable for calculating the area:

Inner Loop Counter - inCount ; Outer Loop Counter - outCount ; Area Variable - maxWater

Now, the outCount moves from 0 to the end of the height array (n), and the inCount from outCount+1 to the end. At every iteration, calculate the water(area) between the 2 counter variables and store it in the maxWater variable. While moving ahead, if the value of maxWater becomes more than its previous value, update its value. Later, return the answer. 

area= (inCount-outCount) * min(height[inCount] * height[outCount]).

Time Complexity:

The time complexity of this method is O(n^2). Why? Because we are using a nested loop and the counter variables traverse over the array twice, making it x2. 

Space Complexity:

During this whole program, we are not creating any other array or data structure so its space complexity remains constant O(1). 

Method 2: Optimal Approach

The previous approach was using a nested loop, therefore the time complexity was O(n^2). What if there was a better solution that performed the same work in lesser time? Let's take a look at this solution. 

In this method, we take 2 variables that point towards the beginning and end of the given array respectively. We set a particular condition at which the first or second variable will move. At the point where the state breaks, we get our answer. Let's see how we can solve this question using this approach. 

Algorithm:

Declare two variables, first=0 and end=n-1, and another variable called maxWater to store the answer(most water in a container). Now, calculate the water between the first and end, taking them as two lines. But, there is a possibility that a greater amount of water is there in other containers. So, you increase the first variable by 1 if height[first] < height[end], otherwise you bring the end variable towards the left by 1. This will ensure you get the right answer by finding out the maximum water and ruling out all the possible answers. 

Time Complexity:

The time complexity here reduces to O(n), making it more efficient than the previous one. Why? Since it does all the checking in a single go, the time gets reduced. 

Space Complexity:

As we are not using any extra space, just like the previous solution, here also it remains constant. 

C++ Code for Finding Container With Most Water

#include
using namespace std;

int maxWater(int height[], int n)
{
    int first = 0;        
    int end = n -1;
    int ans = 0;
    while (first < end){        //putting the condition
        ans = max(ans, min(height[first], height[end]) * (end - first));    //finding out area
	if (height[first] < height[end])
            first += 1;  
        else
	    end -= 1;
	}
    return ans;
}

int main()
{
    int height[]={5,1,3,4,6};
    int n = sizeof(height) / sizeof(height[0]);    //finding size of array
    cout << maxWater(height, n);
	
}

Java Code for Finding Container With Most Water

import java.util.*;
class Water{
	public static int maxWater(int height[], int n)
	{
		int first = 0;
		int end = n -1;
		int ans = 0;
		while (first < end)                  //condition to check
		{
			ans = Math.max(ans, Math.min(height[first], height[end]) * (end - first));	
			//Math.max is a Java function to calculate the maximum amongst the two
			if (height[first] < height[end])               
				first += 1;
			else
				end -= 1;
               }
		return ans;
	}
	
	public static void main(String[] args)
	{
		int height[]={5,1,3,4,6};
		int n = 5;
		System.out.print(maxWater(height, n));
	}
}

Python Code for Finding Container With Most Water

def maxWater(height):
	first = 0
	end = len(height) -1
	ans = 0
	
	while first < end:                   //condition applied
		ans = max(ans, min(height[first], height[end]) * (first - end))
		if height[first] < height[end]:
			first += 1
		else:
			end -= 1
	return ans

# Working Part
height=[5,1,3,4,6]
print(maxWater(height))

Output

20

Summing Up

In this competitive world with more than 23 million software developers, having a cutting edge over other students is crucial for you to land in a product-based company. Companies like Microsoft, Meta, etc are expecting their future employees to have efficient programming skills. Therefore, going for optimal solutions is a good way to ensure your presence at a good company. We, at FavTutor, bring to you the most complex questions with the easiest approach so that you can get not just the solution but the intuition behind it too!