The N-Queens problem is a classical problem that is very important for coding interviews. It demands a deep and crystal clear understanding of the backtracking concept to solve it. So, let's dive deep into N-Queens Problem, but before learning its approach, let's go through the basics. If you are a huge chess fan, you are certainly going to enjoy the journey to the solution.
What is Backtracking?
Let's understand it through an example. Imagine you want to go to a grocery store, but you somehow forget the path and end up at a crossroads. You know that one of the paths is certainly going to take you to the store. What would you do in such a situation? Explore each path one by one.
Well, that's the only option you have. So, you will choose one of the paths and start searching for the store. If the store is not found on path 1 you go back from where you started and explore other paths. This kind of concept is called backtracking.
So, in backtracking we try out one of the moves out of the available moves and try to solve the problem with the selected move. If the problem does get solve we print the solution else we explore all the other moves. And if no move leads you to the solution, we declare that the problem has no solution.
Here are some of the other more popular Backtracking problems to understand the importance of it.
What is N-Queen's problem?
N Queen problem demands us to place N queens on a N x N chessboard so that no queen can attack any other queen directly.
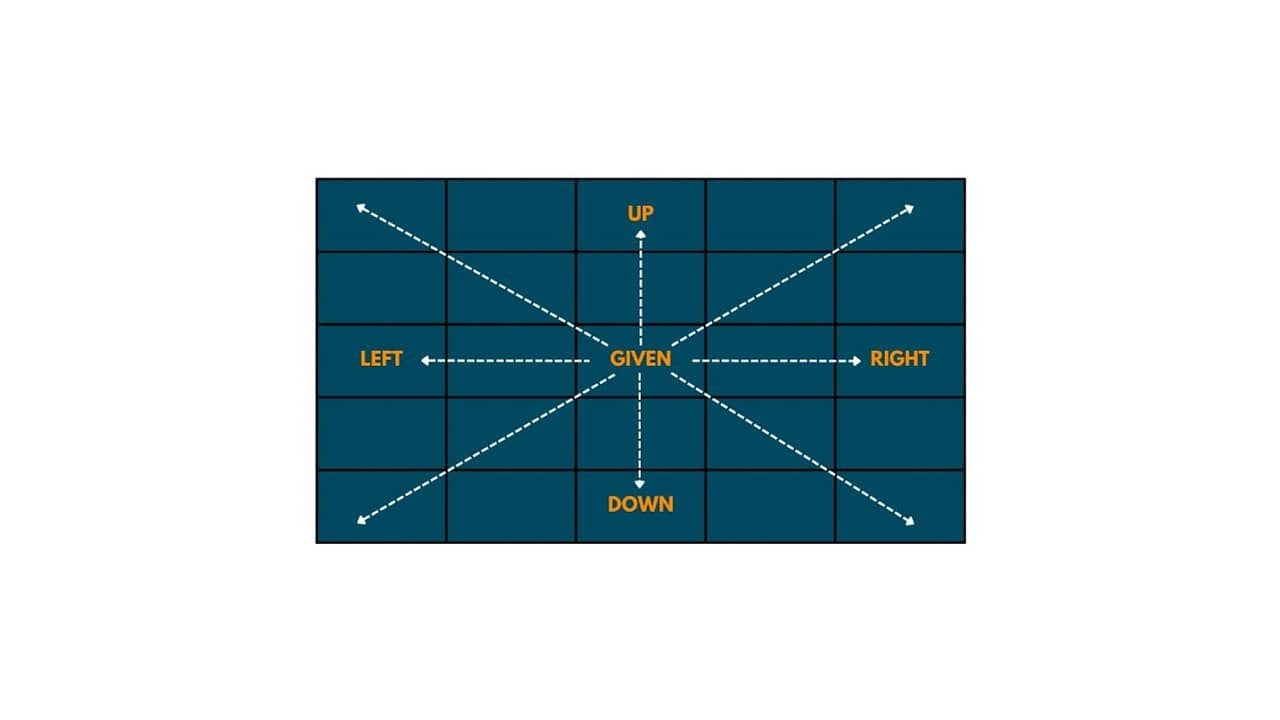
Problem Statement: We need to find out all the possible arrangements in which N queens can be seated in each row and each column so that all queens are safe. The queen moves in 8 directions and can directly attack in these 8 directions only.
Before starting with the actual N queen problem, let's shorten it down to 4 - Queen problem, and then we will generalize it for N.
4 - Queen Problem
This problem demands us to put 4 queens on 4 X 4 chessboard in such a way that one queen is present in each row and column and no queen can attack any other queen directly. this means no 2 or more queens can be placed in the same diagonal or row or column.
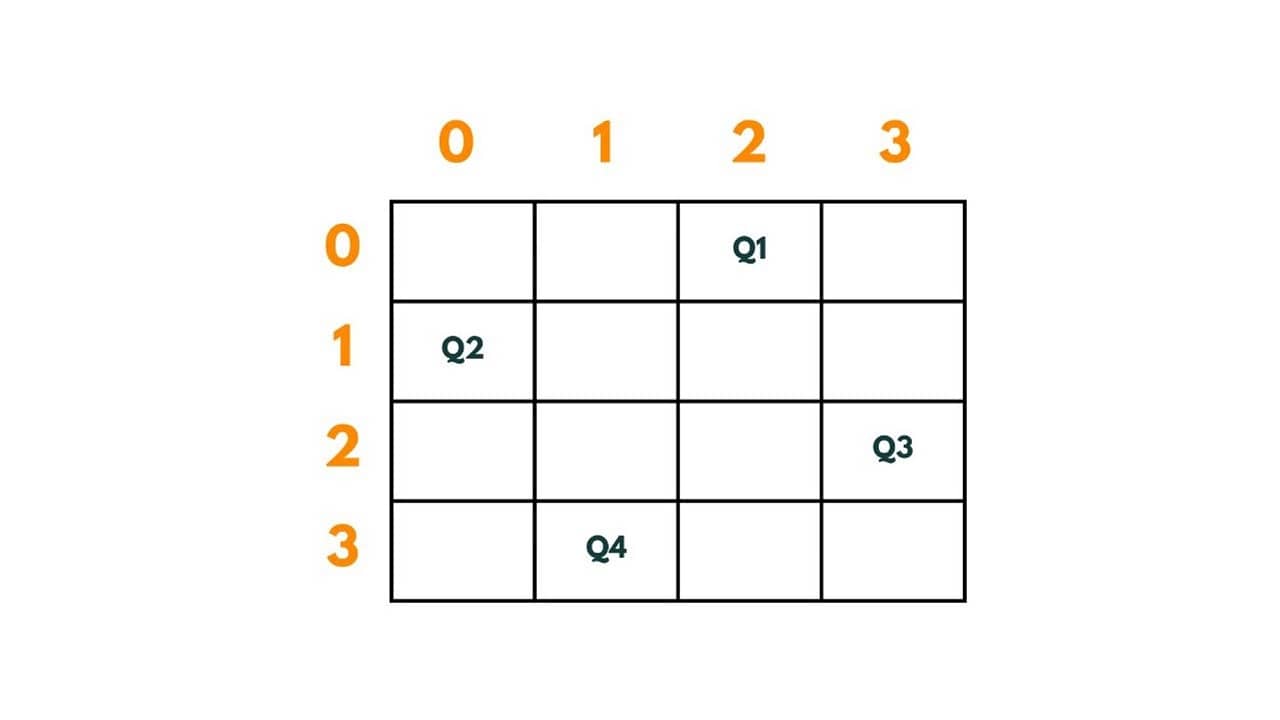
Let's try to put queens Q1, Q2, Q3, and Q4 in the above present chessboard. The first queen i.e. Q1 can be put anywhere on the chessboard as there is no other queen present on the board and hence no restrictions. Therefore putting Q1 at position (0,0). So the path so far is| (0,0)|.
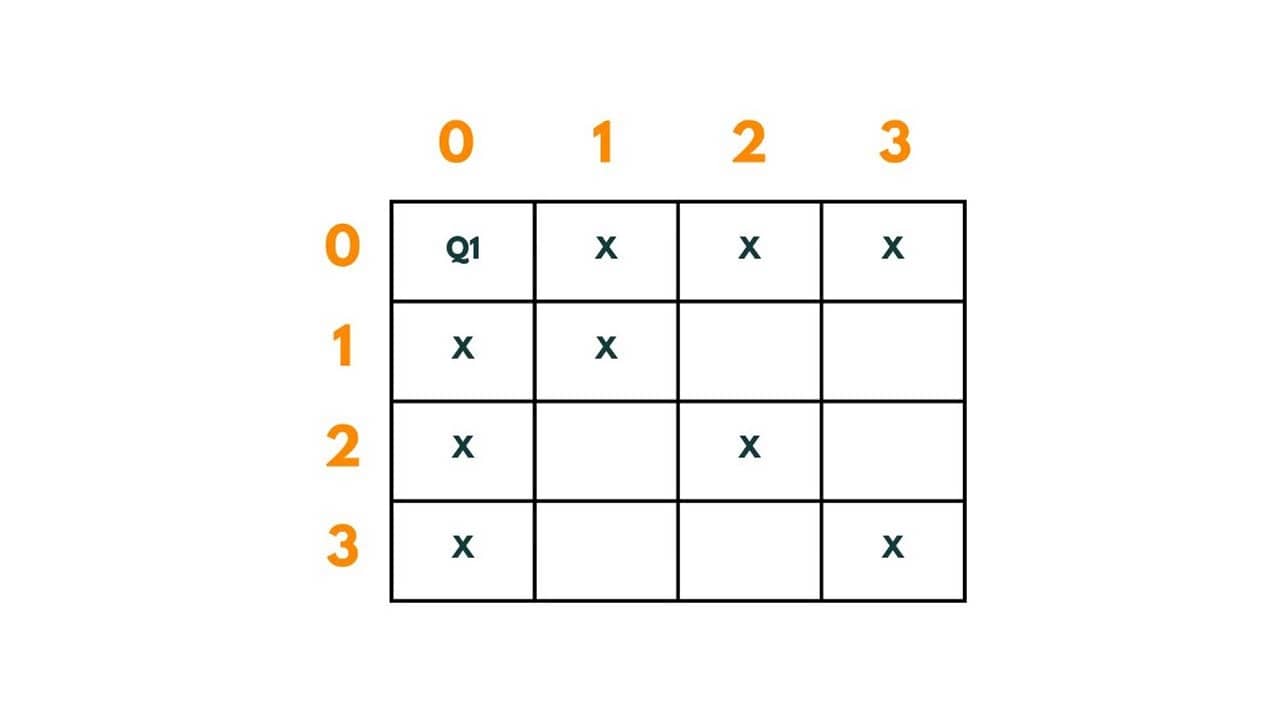
When Q1 has been placed there are some places where the next queens can't be placed to fulfill given conditions. So to put queen Q2 in the second row we have positions - (1,2) and (1,3). Let's put it at (1,2).The path so far is | (0,0) -> (1,2)|
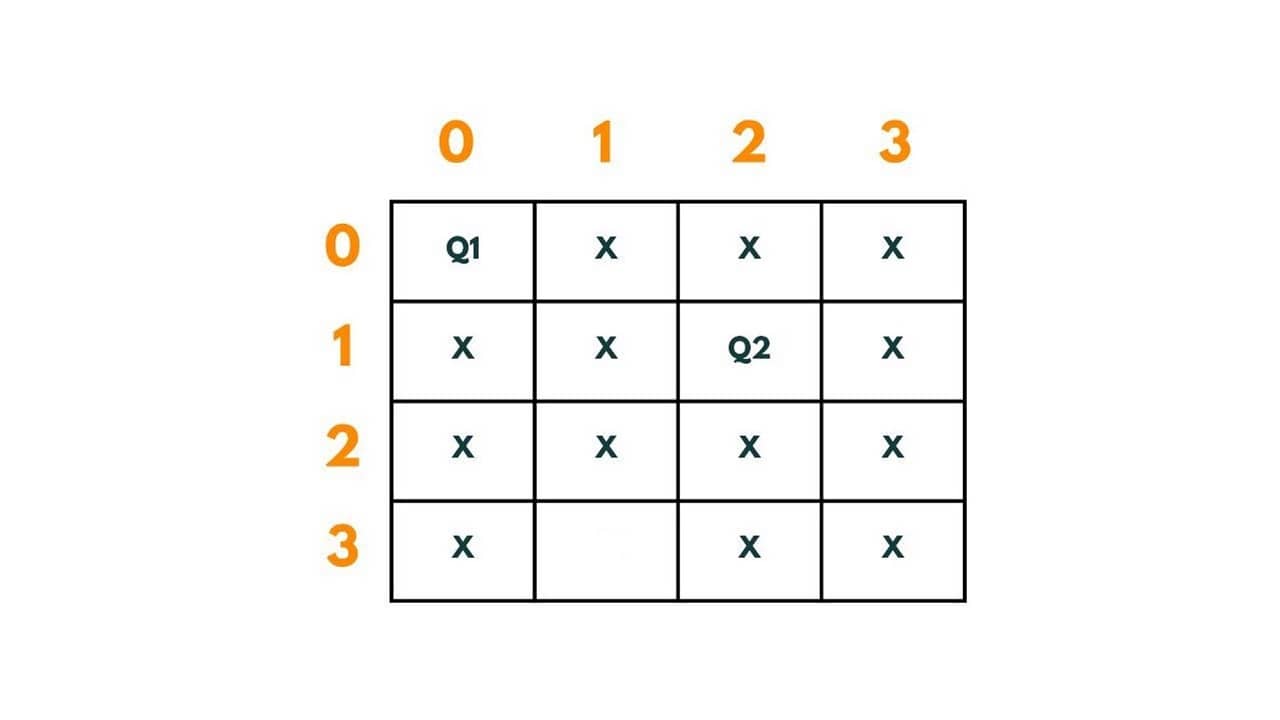
Now this placement of Q2 blocks all the boxes of row 3 and hence there is no way to put Q3. If we put it at (2,0) or (2,2), Q1 will attack it, and at (2,1) and (2,3) Q2 attacks it. Therefore we backtrack from here and revisit the previous solution by readjusting the position of Q2. So instead of putting it at (1,2), we put it at (1,3). The path so far is | (0,0) -> (1,3)|
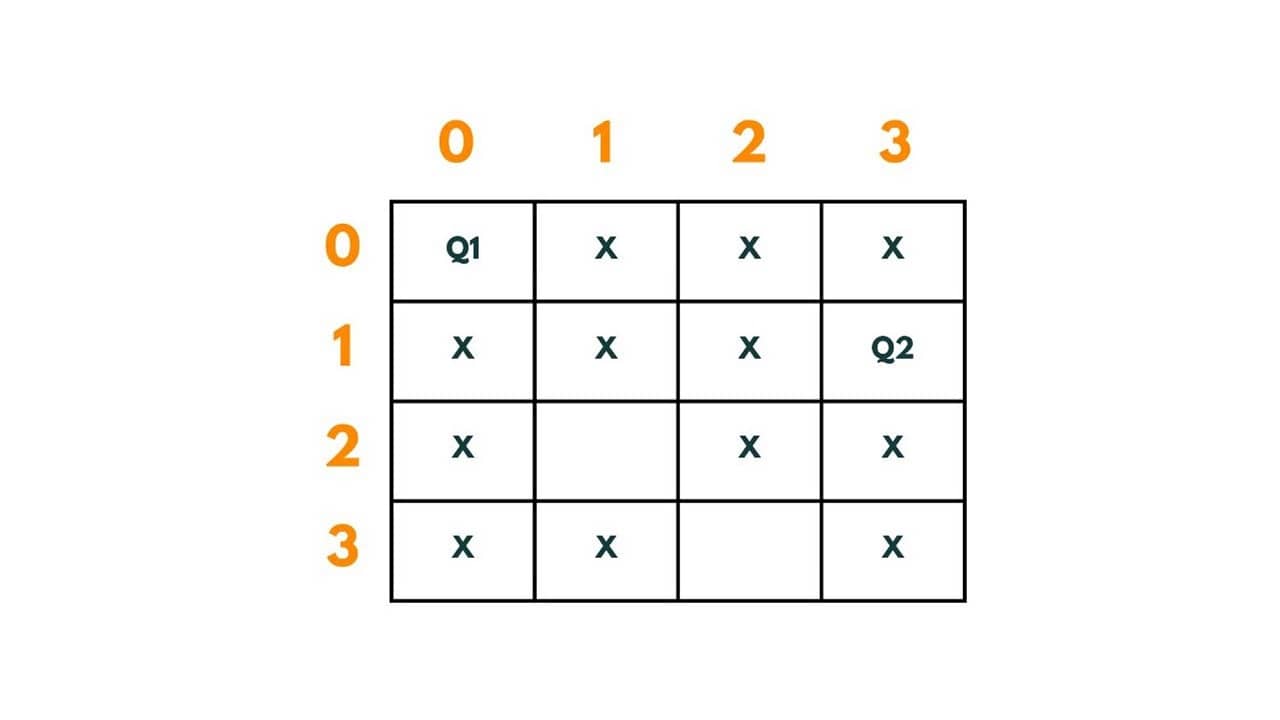
We put Q3 at (2,1). Hence, the path so far is | (0,0) -> (1,3) -> (2,1)|.
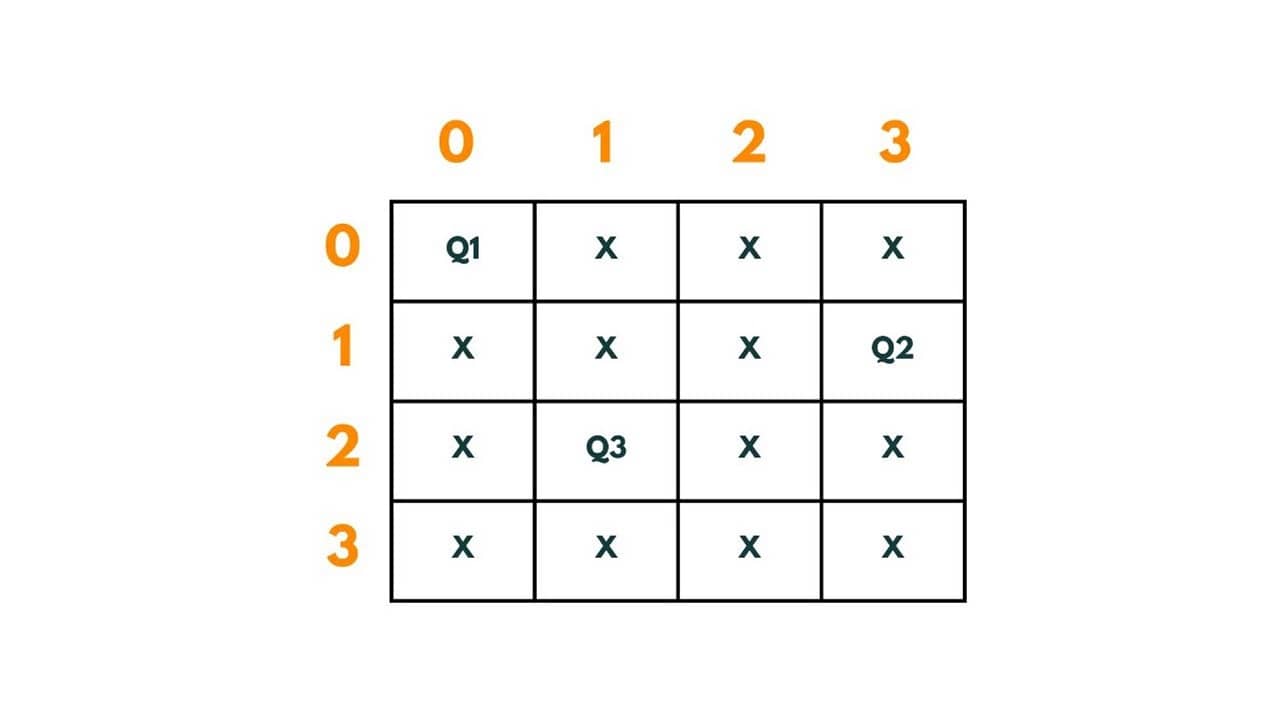
Now again the same problem occurs, there left no box to place Q4. There was only 1 way to place Q3 and all placements of Q2 have been explored, so now we come to Q1 for re-adjustment. We move it from (0,0) to (0,1). The path so far is | (0,1)|.
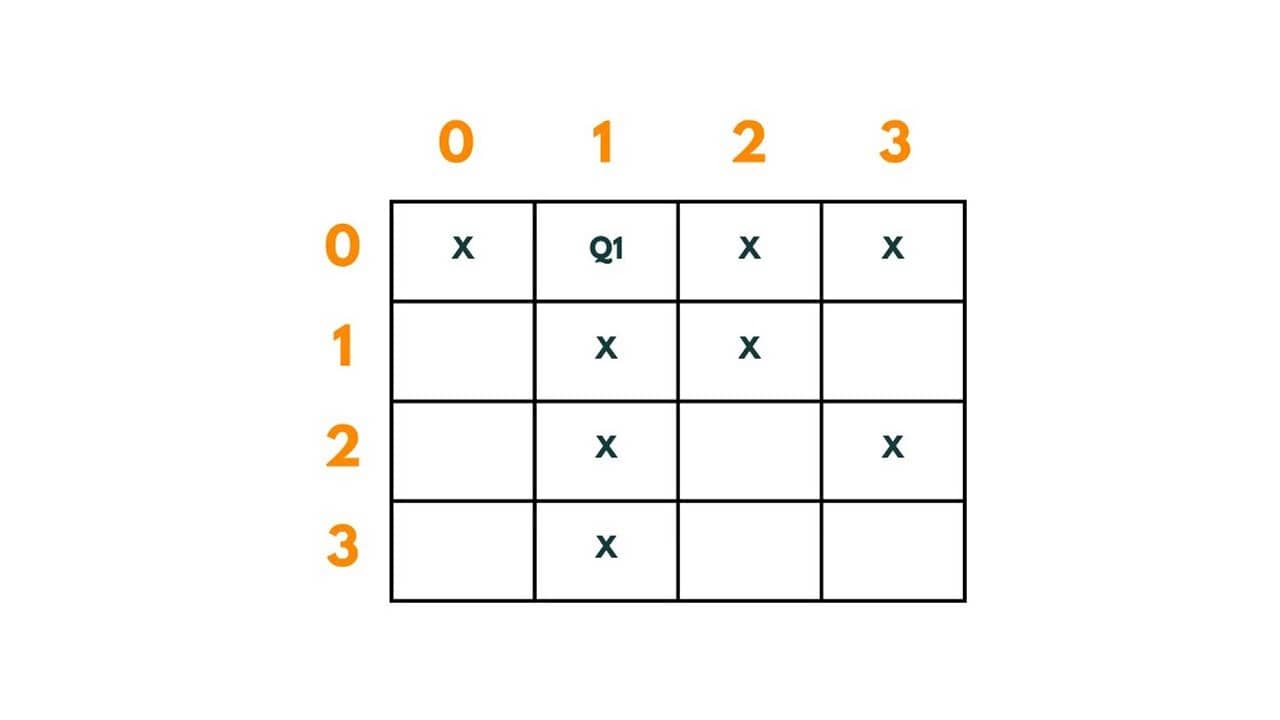
We put Q2 at (1,0). The path so far is | (0,1) -> (1,0)|.
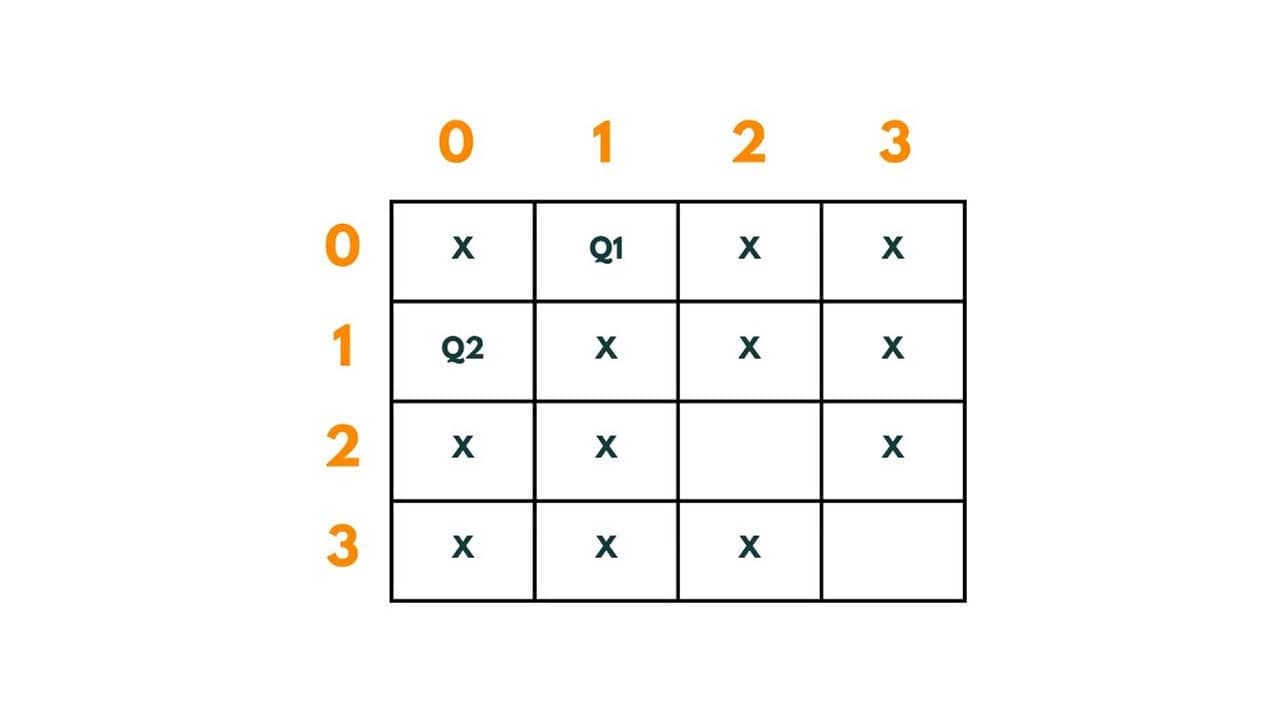
Q3 is put at (2,2). The path so far is | (0,1) -> (1,0) -> (2,2)|.
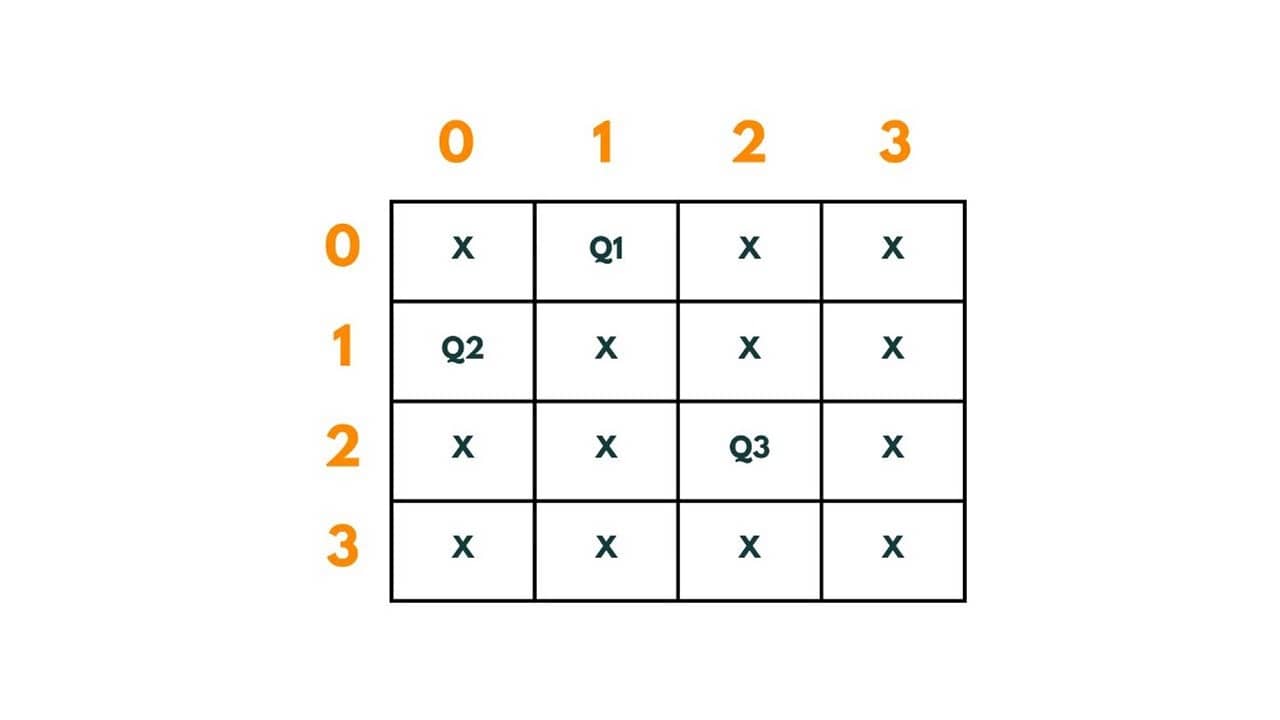
Now again there is no space left for placement of Q4 in row 4. Therefore we again backtrack and readjust position of Q2 from (1,0) to (1,3).The path so far is | (0,1) -> (1,3)|.
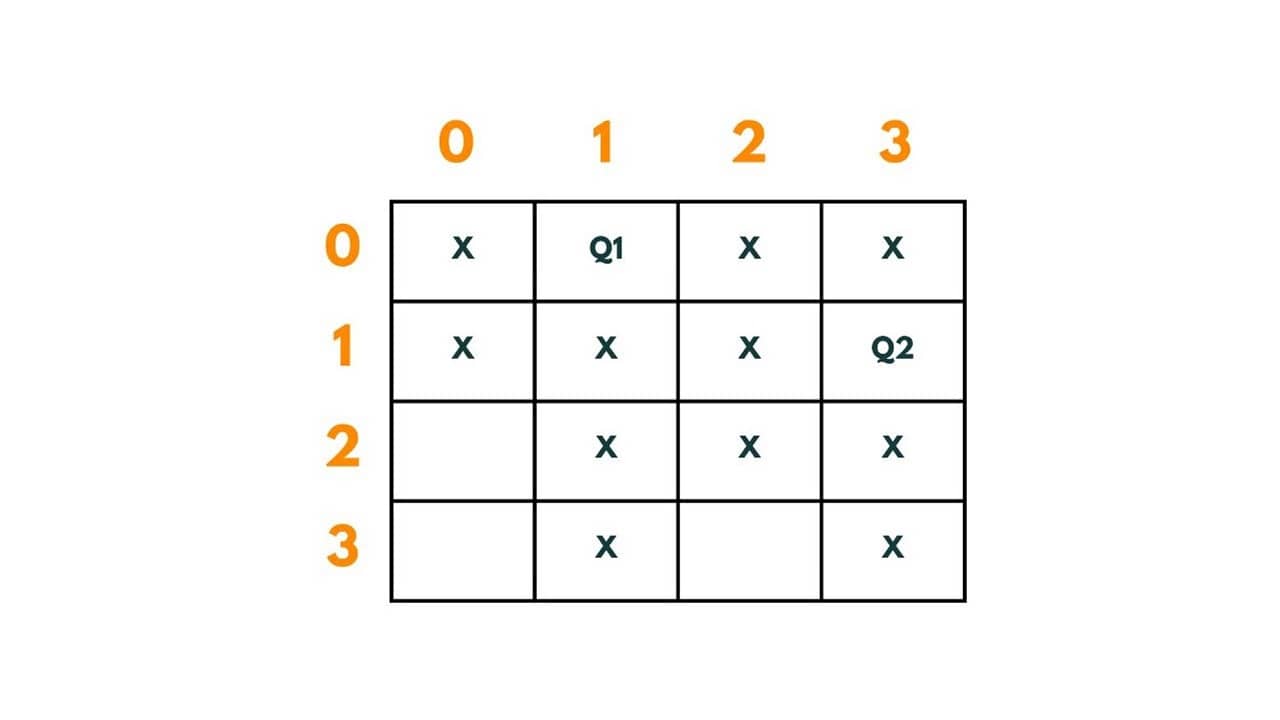
Q3 is put at (2,0). The path so far is | (0,1) -> (1,0) -> (2,0)|.
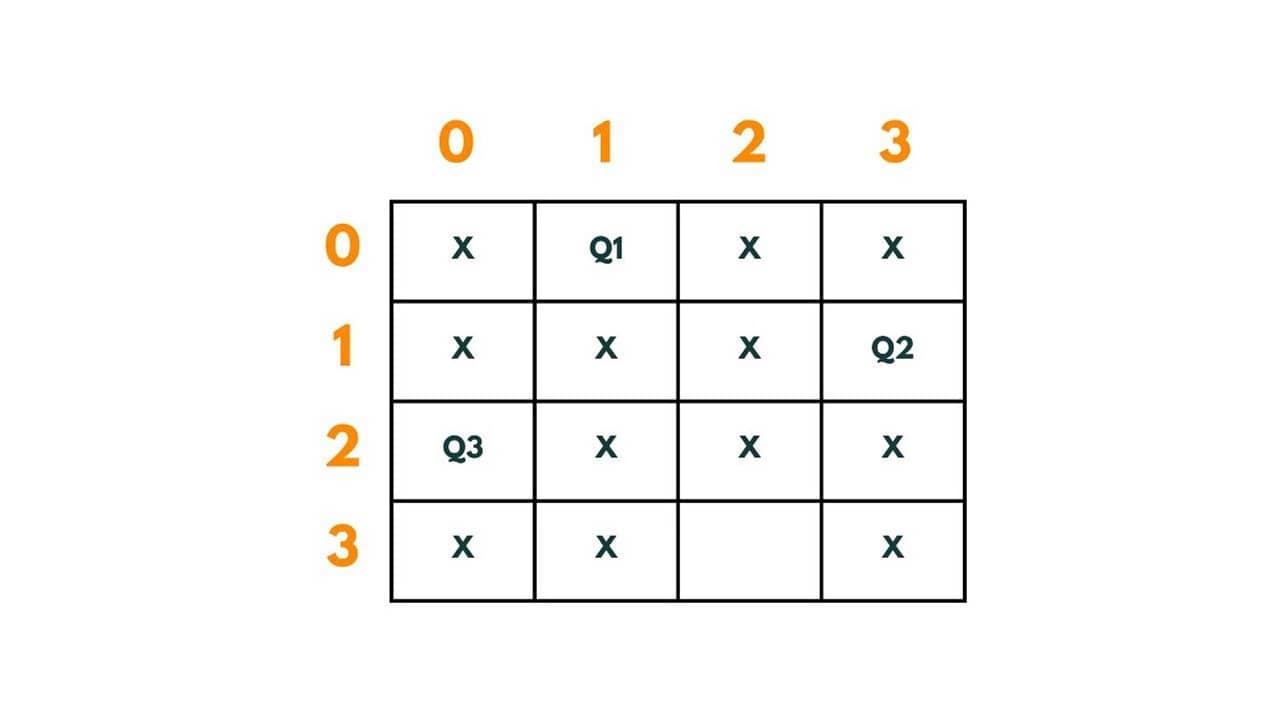
We put Q4 at (3,2). The path so far is | (0,1) -> (1,0) -> (2,0) -> (3,2)|.
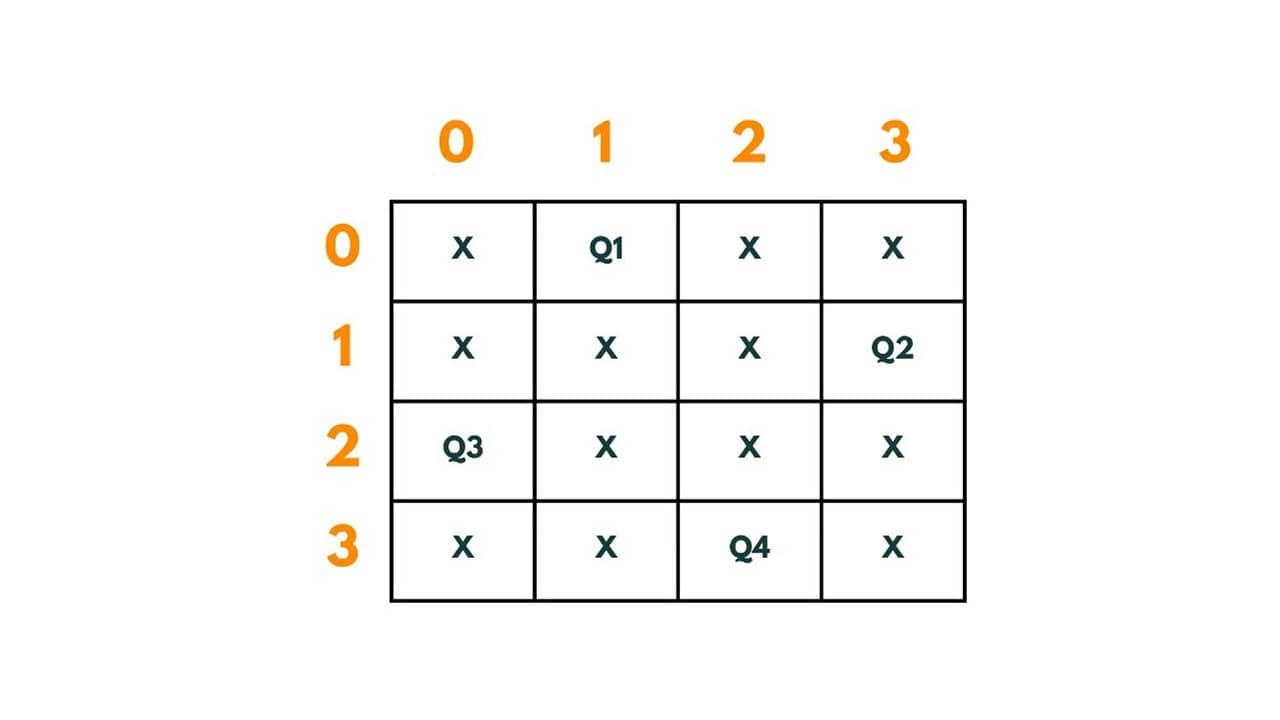
Therefore through backtracking, we reached a solution where 4 queens are put in each row and column so that no queen is attacking any other on a 4 X 4 chessboard.
Another solution can be:
The Easiest Backtracking Approach
The most intuitive approach to solve this problem could be to find out all the possibilities until we find the appropriate arrangement. So whenever we will place any queen on the board we will check if any other queen has been placed in that row/column/diagonal.
N Queen Problem Algorithm
- We create a board of N x N size that stores characters. It will store 'Q' if the queen has been placed at that position else '.'
- We will create a recursive function called "solve" that takes board and column and all Boards (that stores all the possible arrangements) as arguments. We will pass the column as 0 so that we can start exploring the arrangements from column 1.
- In solve function we will go row by row for each column and will check if that particular cell is safe or not for the placement of the queen, we will do so with the help of isSafe() function.
- For each possible cell where the queen is going to be placed, we will first check isSafe() function.
- If the cell is safe, we put 'Q' in that row and column of the board and again call the solve function by incrementing the column by 1.
- Whenever we reach a position where the column becomes equal to board length, this implies that all the columns and possible arrangements have been explored, and so we return.
- Coming on to the boolean isSafe() function, we check if a queen is already present in that row/ column/upper left diagonal/lower left diagonal/upper right diagonal /lower right diagonal. If the queen is present in any of the directions, we return false. Else we put board[row][col] = 'Q' and return true.
Here is the Java code to implement N Queen Problem:
import java.util.*; public class HelloWorld { //this functio checks if the cell in which queen is to placed is safe or not. public static boolean isSafe(int row, int col, char[][] board) { //checking horizontally, if any other queen has been already placed in that row. for(int j=0; j<board.length; j++) { if(board[row][j] == 'Q') { return false; } } //checking vertically, if any other queen has been already placed in that column. for(int i=0; i<board.length; i++) { if(board[i][col] == 'Q') { return false; } } //checking if queen has been already placed in that upper left diagonal int r = row; for(int c=col; c>=0 && r>=0; c--, r--) { if(board[r][c] == 'Q') { return false; } } //checking if queen has been already placed in that upper right diagonal r = row; for(int c=col; c<board.length && r>=0; r--, c++) { if(board[r][c] == 'Q') { return false; } } //checking if queen has been already placed in that lower left diagonal r = row; for(int c=col; c>=0 && r<board.length; r++, c--) { if(board[r][c] == 'Q') { return false; } } //checking if queen has been already placed in that lower right diagonal for(int c=col; c<board.length && r<board.length; c++, r++) { if(board[r][c] == 'Q') { return false; } } return true; } // to save each arrangement present in board of characters, we first convert it as board of string and then save the list in all boards (which is list of lists of string) public static void saveBoard(char[][] board, List<List<String>> allBoards) { String row = ""; // this will contain the arrangement of board as string List<String> newBoard = new ArrayList<>(); //traversing through the board of characters and saving each row as string in newBoard for(int i=0; i<board.length; i++) { row = ""; for(int j=0; j<board[0].length; j++) { if(board[i][j] == 'Q') row += 'Q'; else row += '.'; } newBoard.add(row); } // adding the list "new board" to list of lists of string called "allBoards" allBoards.add(newBoard); } //recursive function that explore possible moves to place a queen column by column public static void solve(char[][] board, List<List<String>> allBoards, int col) { // if column length becomes equal to board.length, that implies all the columns have been explored and function solve is ready with its solution. if(col == board.length) { // when we have one of the ways to put queens, we save it as a list called "board" in list of lists "allboards" that contains all the possible solutions. saveBoard(board, allBoards); return; } // here we move column by column to place each queen in each column for(int row=0; row<board.length; row++) { // if the queen is safe to be put in the cell, we put 'Q' in that cell to know that queen has been placed if(isSafe(row, col, board)) { board[row][col] = 'Q'; //we again call the solve function by incrementing the column by 1. solve(board, allBoards, col+1); // while backtracking, we put '.' in each cell showing that no queen has been placed there as in to again, to explore other solution or moves we need a clear board. board[row][col] = '.'; } } } public static void solution(int n) { //all boards will contain lists that are the possible solutions. List<List<String>> allBoards = new ArrayList<>(); // each board would be of character so that we can put 'Q' to refer to queen placement and '.' to refer that no queen is placed there. char[][] board = new char[n][n]; // calling the solve function to begin finding the possible arrangements solve(board, allBoards, 0); //printing the list of all solutions. for(List<String> aboard : allBoards){ for(int i=0; i < aboard.size(); i++){ System.out.println(aboard.get(i)); } System.out.println(); } } public static void main(String[] args){ solution(4); } }
Output:
..Q. Q... ...Q .Q.. .Q.. ...Q Q... ..Q.
Time & Space Complexity
As we got to know in the algorithm for each cell, to check if the queen can be placed there or not, we are iterating for N times. So the recurrence relation comes out to be:
T(N) = N * T(N-1) + N.
T(N-1) = N * T(N-2) + N
---------------------------
----------------------------
T(1) = 1
This totals T(N) = N* N!. therefore, the time complexity comes out to be O(N * N!).
And as we have used an extra board of characters of N x N Size, The space complexity comes out to be O(N *N).
Optimized Branch and Bound Approach
As we saw in the previous approach that for each cell we check all the possible directions if the queen has been placed there or not. We again and again check these directions due to which the time complexity increases. So we can optimize it well by taking into count some important mathematical phenomena.
We will optimize the isSafe() function by keeping track if, for a cell, the queen has been placed in any of the directions. We found the directions in which the queen has been already placed therefore this approach is popularly known as the branch and bound approach.
N Queen Problem Algorithm for Branch & Bound Approach
Step 1: To block the path of upcoming queens in a column where a queen is already present, we will maintain a boolean array colCount that keeps track of queens present in every column. It will hold true for all the columns having a queen.
Step 2: To block normal diagonals, in every cell of the chessboard we will put rowNumber + colNumber as:
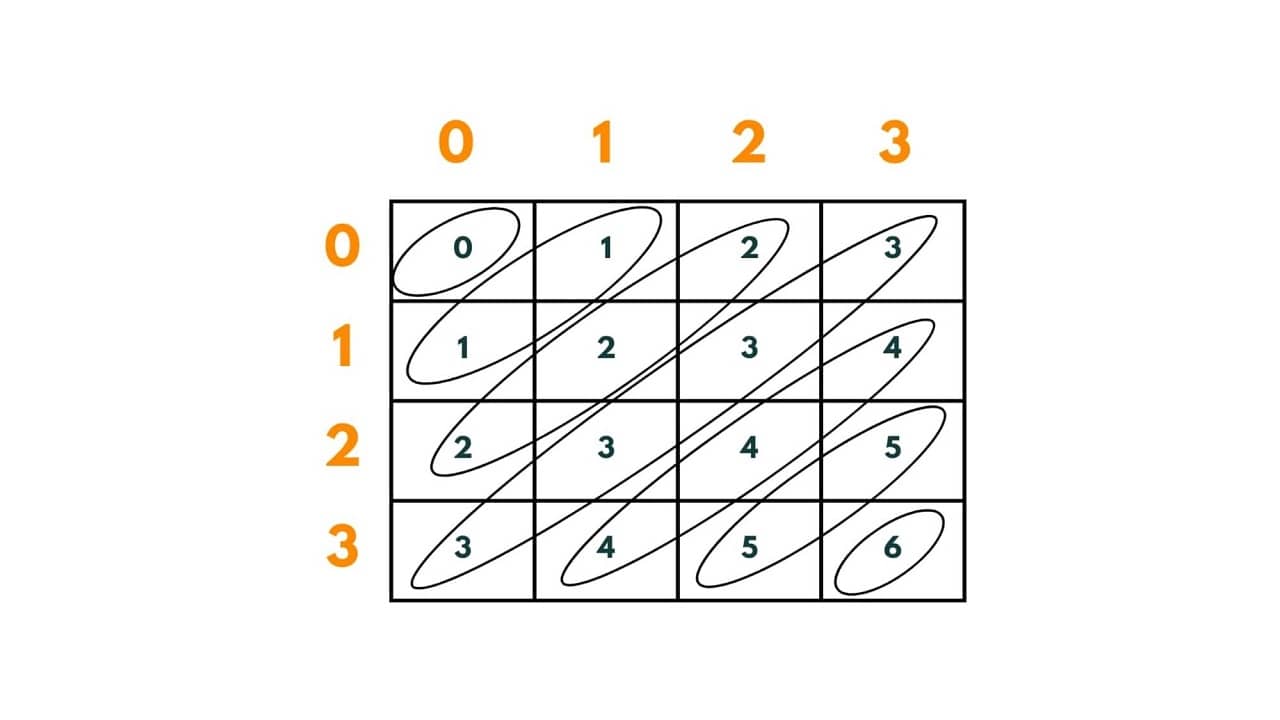
There is an important thing to notice here that is, every diagonal has a unique value. Total (normal) diagonals in any N x N chessboard = 2* (N-1). We will create a boolean array of size 2*(N-1) and map the array index with the row+column of the cell. It will keep track of the queen sitting in a diagonal by putting true at the index that equals to row+col where the queen is sitting.
Therefore, whenever placing a queen we will check if the normal diagonal array at the row+column index is false or not.
Step 3: To block reverse diagonals, in every box of the chessboard we will put rowNumber - colNumber as:-
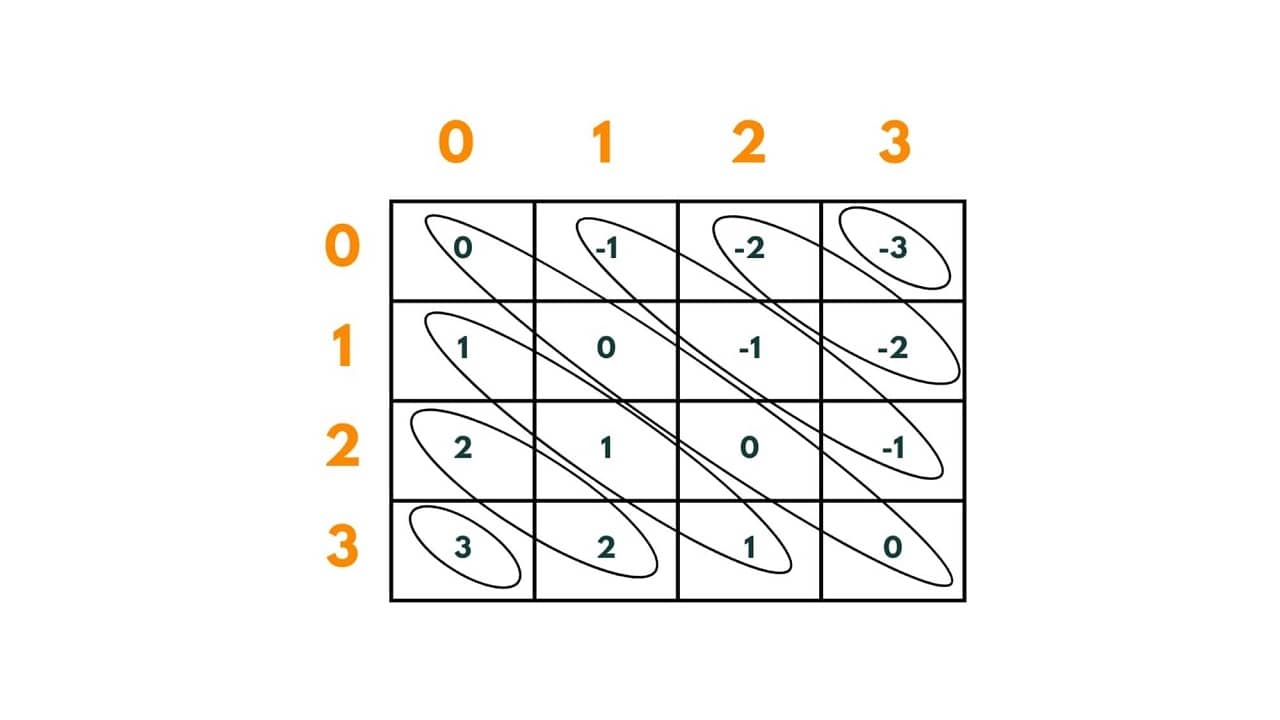
Again, there is an important thing to notice here that every diagonal has a unique value. Total (reverse) diagonals in any N x N chessboard = 2* (N-1).
But as you can see here, we have negative values too and it is impossible to map them to any index of the array. To remove negative values we add (chessboard length - 1 ) to each (row-column) number so that we can adjust and easily map these values to the index of an array.
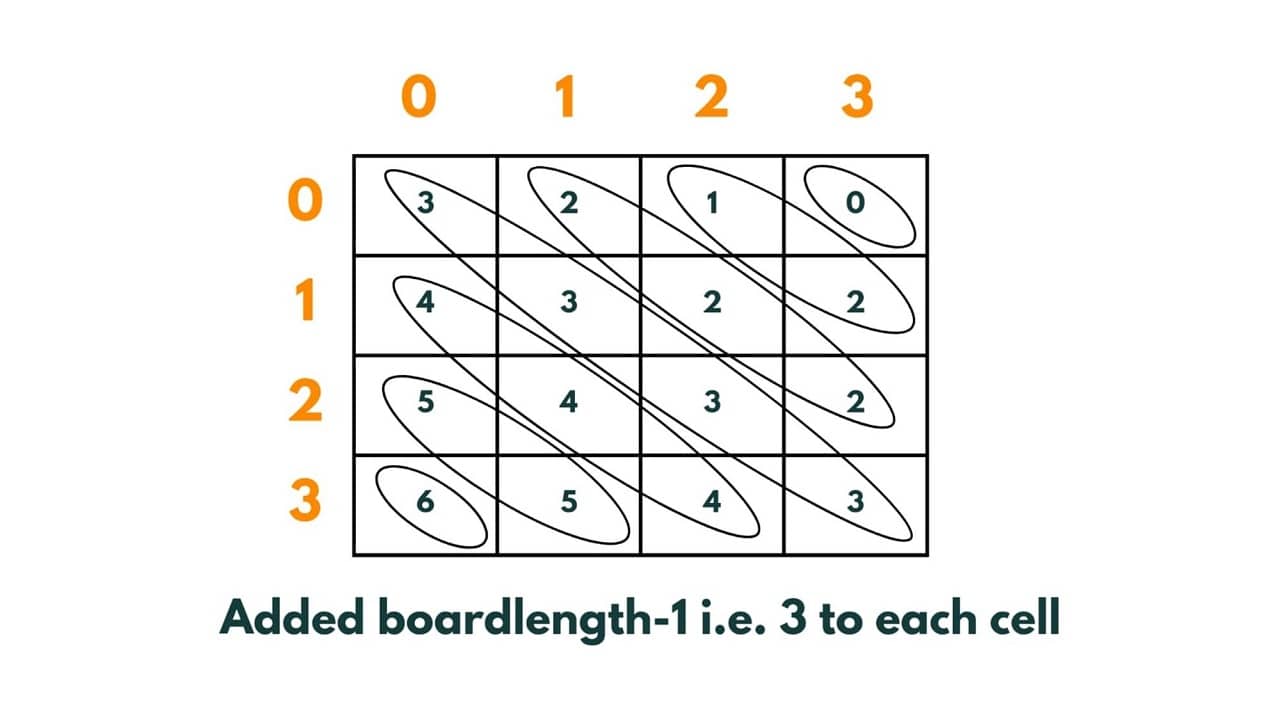
So now the values vary from 0 to 6 and can be easily mapped to an array. We will create a boolean array of size 2*(N-1) that will keep track of the queen sitting in a reverse diagonal by putting true at the index that equals to [ (row-col) + (boardlength -1) ]where the queen is sitting.
Step 4: Then we create a recursive function solve and pass board, row index as 0 and all the 3 boolean arrays and a string named path so far.
Step 5: Now we explore all the columns present on board and try to place the queen at every possible position.
Step 6: if { colCount [column] and normal Diagonal [row + col] and reverseDiagonal[row - col +board.length -1] is false} then the queen can be placed at that row and col.
Step 7: We mark the column, normal diagonal, and reverse diagonal as true where the queen has been seated. And then we again call solve() function and pass the row as row+1 and add (row,col) to the path so far string.
Step 8: The base case for the recursive function would be -> If row becomes equal to board.length, that means the solution has been found and hence we print the path so far and return.
Here is the code in Java for branch and bound approach to solve N Queen Problem:
class nQueens { public static void main(String[] args) { int n = 4; //creating a boolean matrix to place true at places where queen is being placed. boolean board[][] = new boolean [n][n]; // to keep a count of the columns where queens have been placed. boolean[] colCount = new boolean[board[0].length]; //it keeps a track of all the normal diagonals where next queens can't be or can be put. boolean[] normalDiag = new boolean [2*(n-1)]; //it keeps a track of all the reverse diagonals where next queens can't be or can be put. boolean[] reverseDiag = new boolean [2*(n-1)]; //to print the arrangement where queens can be put on board. String pathSoFar = ""; //calling a recursive function which through backtracking, provide us a solution. //passing row as 0 so that we start exploring the options from base i.e row1 i.e 0. solve(board,0,colCount,normalDiag,reverseDiag,pathSoFar); } public static void solve(boolean[][] board, int row, boolean[] colCount, boolean[] normalDiag, boolean[] reverseDiag, String pathSoFar) { // if row becomes equal to board length that implies all the available options have been explored and the function "solve" is ready with its solution. if (row == board.length) { System.out.print("Queens can be seated as "+ pathSoFar + "." +"\n"); return; } // we will try exploring all the columns of a row where queen can be seated. for (int col = 0; col < board.length; col++) { // if a certain column has no restrictions and any other queen can't attack it, we place the queen at that col,in that particular row. if (colCount[col] == false && normalDiag[row + col] == false && reverseDiag[row - col + board.length - 1] == false) { // marking the col and row of that board matrix true showing that queen has been placed here. board[row][col] = true; //blocking the column, normal diagonal and reverse diagonal where queen has been placed so that no other queen can be placed there. colCount[col] = true; normalDiag[row + col] = true; reverseDiag[row - col + board.length - 1] = true; // we call solve function again with an increment in row count so that we explore the next row and next queen can be seated. solve(board, row + 1, colCount, normalDiag, reverseDiag, pathSoFar + row + "-" + col + ", "); // after we return, we mark all the places false which were marked true before, as to again explore a new path we need a clear board. board[row][col] = false; colCount[col] = false; normalDiag[row + col] = false; reverseDiag[row - col + board.length - 1] = false; } } } }
Output:
Queens can be seated as 0-1, 1-3, 2-0, 3-2. Queens can be seated as 0-2, 1-0, 2-3, 3-1.
Time & Space Complexity
As in the optimized approach, we need not iterate over rows or columns or diagonals for each cell if it is valid or not, we get the recurrence relation as:
T(N) = N * T(N-1)
T(N-1) = N * T(N-2)
---------------------------
----------------------------
T(1) = 1
This totals T(N) = N! Therefore, the time complexity comes out to be O(N!).
And as we have used a 2-D array of boards and three 1-D arrays, the space taken by them is - N^2, 2*(N-1), 2*(N-1), N. The total space complexity comes out to be O(N^2).
Conclusion
The N-Queens is a classical problem that beautifully uses the concept of backtracking and provides us an in-depth knowledge of this concept. The approaches we learned in this problem can be used in other problems too and they are important from an interview point of view too.








