Symmetric Tree: How to Check if a Binary Tree is Symmetric?

The symmetric tree is an interesting topic in programming and data structures, where the symmetry gives rise to intriguing algorithms for the traversal of the tree structure. In this article, we will learn about the concept of a symmetric tree, and how to implement it recursively and iteratively.

What is a Symmetric Tree?

A symmetric tree is a binary tree where the left and right sub-trees of each node are identical in structure and the values of the corresponding nodes are also equal. In simpler terms, a symmetric tree can be folded in half along its center and the two halves match each other. It is also called a mirror tree.

For example, consider the following binary tree:

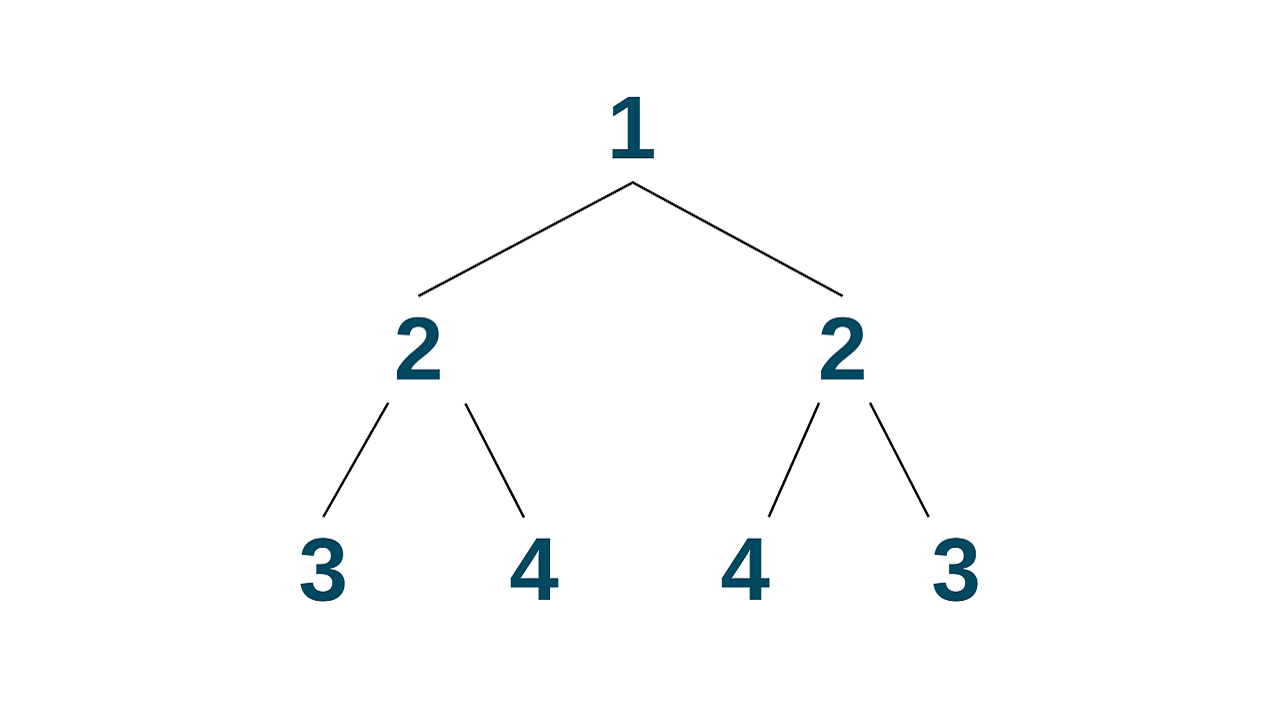
This is a symmetric tree since the left and right sub-trees of each node are identical and the corresponding nodes have equal values.

To check if a given binary tree is symmetric or not, we can recursively compare the left and right sub-trees of the root node. If both the sub-trees are identical and the corresponding nodes have equal values, then the binary tree is symmetric.

Let's take an example to understand the concept in a better way. Consider the following binary tree:

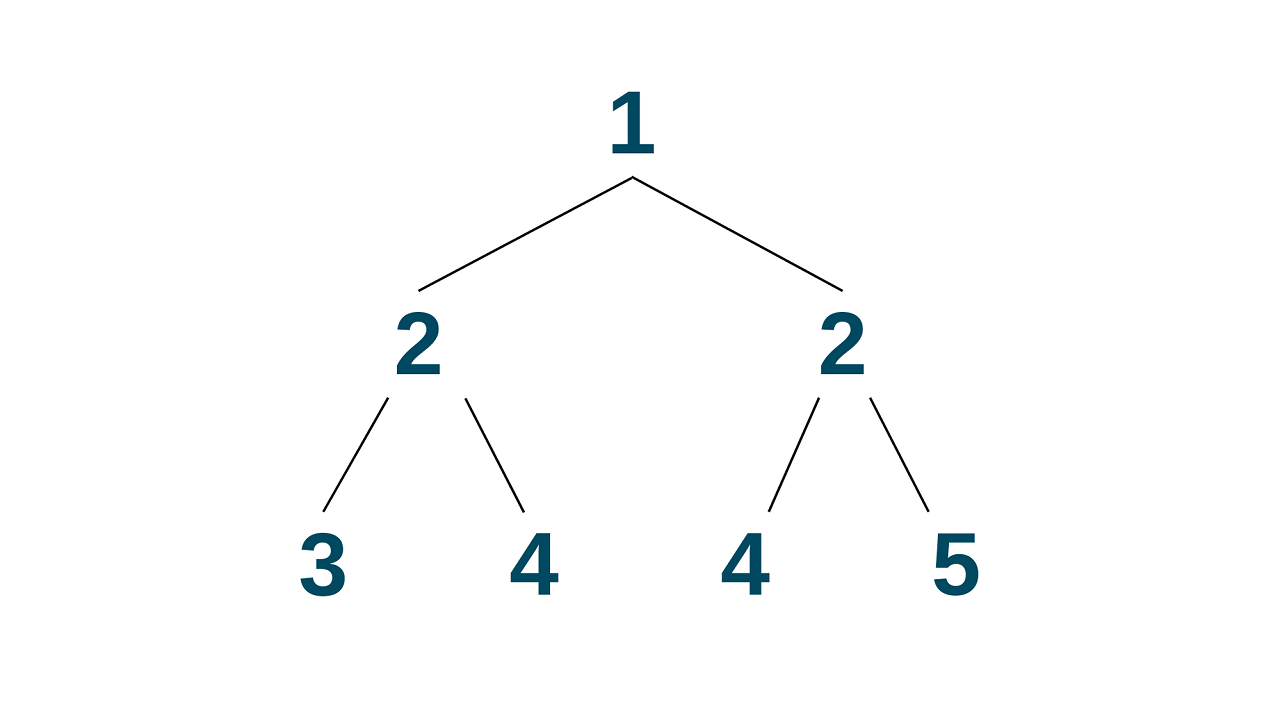
This is not a symmetric tree since the left and right sub-trees of the root node are not identical. The left sub-tree has a node with a value of 3, while the right sub-tree has a node with a value of 5.

How to Check if the Binary Tree is Symmetric?

We can check if a given binary tree is symmetric or not by comparing the left and right sub-trees of the root node. If both the sub-trees are identical and the corresponding nodes have equal values, then the binary tree is symmetric.

To check if the left and right sub-trees of a node are identical, we can recursively compare their respective left and right sub-trees.

Now, let's see how to check if a given binary tree is symmetric or not. Here is the algorithm for this purpose:

1. Check if the root node is NULL. If it is NULL, then the binary tree is symmetric. Return true.
2. Recursively compare the left and right sub-trees of the root node.
3. If both the sub-trees are identical and the corresponding nodes have equal values, then the binary tree is symmetric. Return true.
4. If either of the sub-trees is NULL or the corresponding nodes have unequal values, then the binary tree is not symmetric. Return false.

C++ Implementation

Below is the C++ code to implement the above algorithm to check if a tree is symmetric or not:

#include
using namespace std;

// Definition of binary tree node
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

bool isMirror(TreeNode* left, TreeNode* right) {
    if (left == NULL && right == NULL) {
        return true;
    }
    if (left == NULL || right == NULL) {
        return false;
    }
    return (left->val == right->val) && isMirror(left->left, right->right) && isMirror(left->right, right->left);
}

bool isSymmetric(TreeNode* root) {
    if (root == NULL) {
        return true;
    }
    return isMirror(root->left, root->right);
}

int main() {
    // Creating a sample binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(2);
    root->left->left = new TreeNode(3);
    root->left->right = new TreeNode(4);
    root->right->left = new TreeNode(4);
    root->right->right = new TreeNode(3);

    // Checking if the binary tree is symmetric or not
    if (isSymmetric(root)) {
        cout << "The given binary tree is symmetric." << endl;
    }
    else {
        cout << "The given binary tree is not symmetric." << endl;
    }
    return 0;
}

Output:

The given binary tree is symmetric.

The given C++ code checks whether a binary tree is symmetric or not using a recursive approach. The time and space complexity of this algorithm depends on the number of nodes in the binary tree.

Space & Time Complexity

The time complexity of the isMirror function is O(N), where N is the number of nodes in the binary tree. This is because we are visiting each node only once and performing constant time operations on each node. The isSymmetric function calls isMirror twice, once for the left and once for the right sub-tree, so its time complexity is also O(N).

The space complexity of the isMirror function is O(H), where H is the height of the binary tree. This is because the function calls itself recursively for the left and right sub-trees, and the maximum depth of the recursive call stack is the height of the binary tree. The isSymmetric function also calls isMirror recursively twice, once for the left and once for the right sub-tree.

Iterative Approach

To check if a binary tree is symmetric iteratively, we can use a queue to perform a level-order traversal of the tree. At each level, we compare the values of the nodes in pairs, starting from the outermost nodes and moving inwards.

Here is the algorithm to check if a binary tree is symmetric iteratively:

1. Check if the root node is NULL, if so return true.
2. Create a queue and push the root node and its mirror node (right node followed by left node) onto the queue.
3. While the queue is not empty, dequeue two nodes and compare their values: a. If both nodes are NULL, continue to the next pair of nodes. b. If only one node is NULL or their values are not equal, return false. c. If both nodes are not NULL and their values are equal, push their left and right sub-trees onto the queue in the following order: the left node of the first node followed by the right node of the second node, and the right node of the first node followed by the left node of the second node.
4. If the queue is empty and all pairs of nodes were found to be symmetric, return true.

Here is the C++ code for checking if a binary tree is symmetric iteratively:

#include
#include

using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

bool isSymmetric(TreeNode* root) {
    if (root == NULL) {
        return true;
    }
    queue<TreeNode*> q;
    q.push(root);
    q.push(root);
    while (!q.empty()) {
        TreeNode* node1 = q.front();
        q.pop();
        TreeNode* node2 = q.front();
        q.pop();
        if (node1 == NULL && node2 == NULL) {
            continue;
        }
        if (node1 == NULL || node2 == NULL || node1->val != node2->val) {
            return false;
        }
        q.push(node1->left);
        q.push(node2->right);
        q.push(node1->right);
        q.push(node2->left);
    }
    return true;
}

int main() {
    // Create a binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(2);
    root->left->left = new TreeNode(3);
    root->left->right = new TreeNode(4);
    root->right->left = new TreeNode(4);
    root->right->right = new TreeNode(3);

    // Check if the binary tree is symmetric
    if (isSymmetric(root)) {
        cout << "The binary tree is symmetric." << endl;
    } else {
        cout << "The binary tree is not symmetric." << endl;
    }

    return 0;
}

Output:

The binary tree is symmetric.

The time complexity of this algorithm is O(N), where N is the number of nodes in the binary tree since we are visiting each node once. The space complexity is O(N/2) since the maximum number of nodes in the queue at any given time is N/2 (for a complete binary tree).

Also, learn how to burn a binary tree as well.

Conclusion

We explained what is a symmetric tree and how to check if a binary tree is symmetric or not. Symmetric trees are very useful in cryptography as a form of encryption, computer graphics, and natural language processing. They can be used to efficiently represent complex shapes and objects. In Natural language processing, they can also represent the syntactic structure of sentences in natural language.