Burning a Binary Tree Problem (Find Minimum Time Taken)

Binary trees are a fundamental data structure in computer science. While traversing a binary tree is a common operation, sometimes we need to destroy a binary tree quickly and efficiently, such as when we want to free up memory. In this article, we will explore the minimum time required to burn a binary tree.

What is a Binary Tree?

Before we delve into this problem, let's first understand what a binary tree is.

A binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. The first node in a binary tree is called the root node. The nodes that do not have any children are referred to as leaf nodes. 

The main characteristic of a binary tree is that each node can have a maximum of two child nodes. It is used to represent hierarchical relationships between objects. These are commonly used to implement other data structures and algorithms.

What is Burning Binary Tree?

A burning binary tree is where each node represents a house, and the value in each node represents the time it takes for that house to catch fire. The fire spreads from one node to its left and right children in one unit of time. Once a house catches fire, it cannot be extinguished.

So, let's now understand the problem statement for this burning tree problem.

You are given a binary tree and a target node that has been set on fire. The fire spreads to all nodes connected to the target in one second, including its parent, left child, and right child. You need to find the minimum time required to burn the complete binary tree.

So, given a binary tree and a target node, we need to implement a function to find the minimum time required to burn the complete binary tree if the target is set on fire, where in 1 second, all nodes connected to a given node get burned.

Understanding the problem through an example:

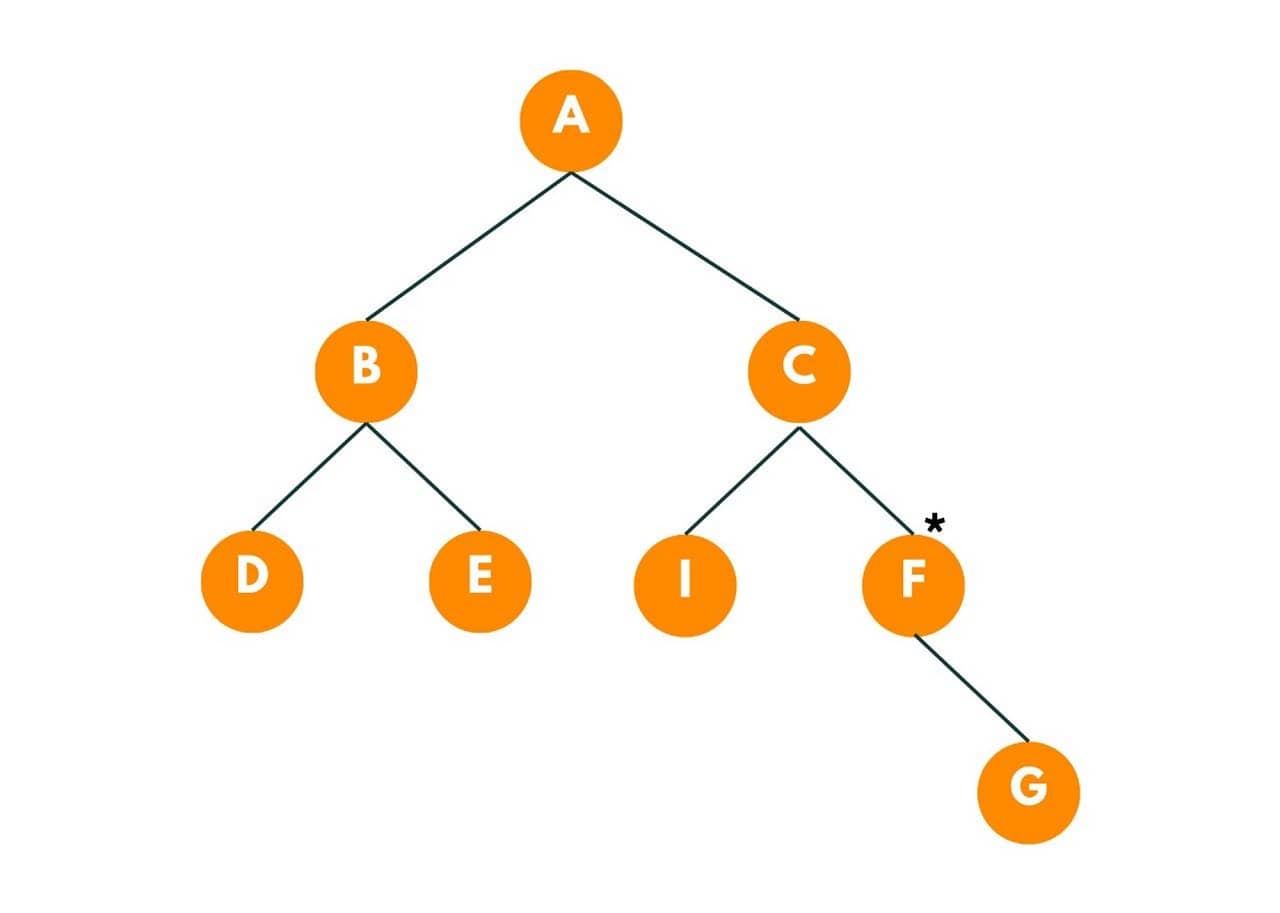
Given this binary tree and the target as 'F', let's see how much time the burning takes place in this tree. Here, the star symbol,*, represents that the node is on fire.

So in the 1st second, all its adjacent neighbors of the given node will burn. So, G and C nodes get burnt. Time = 1 second.

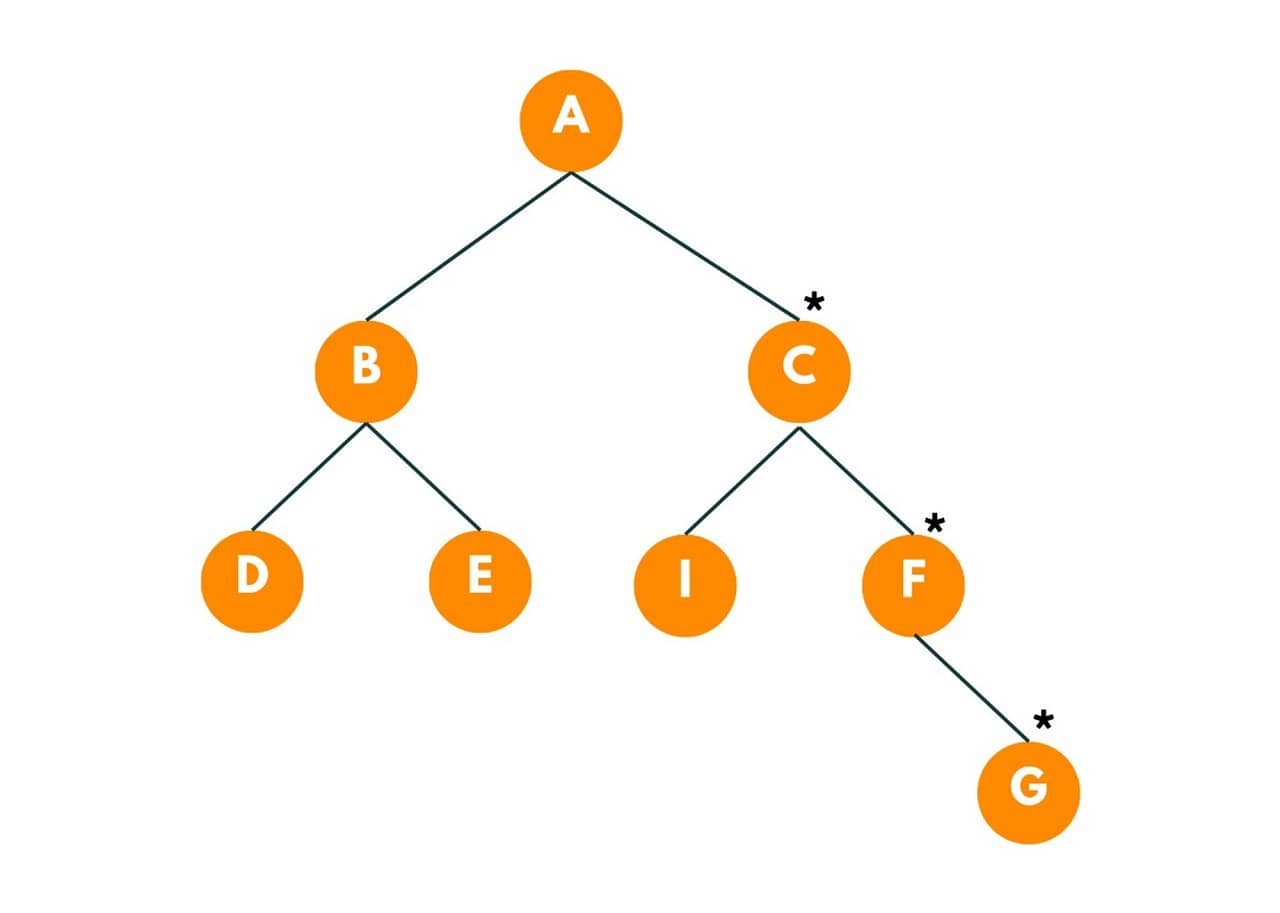
In the next second, A and I burn. Time = 2 seconds.

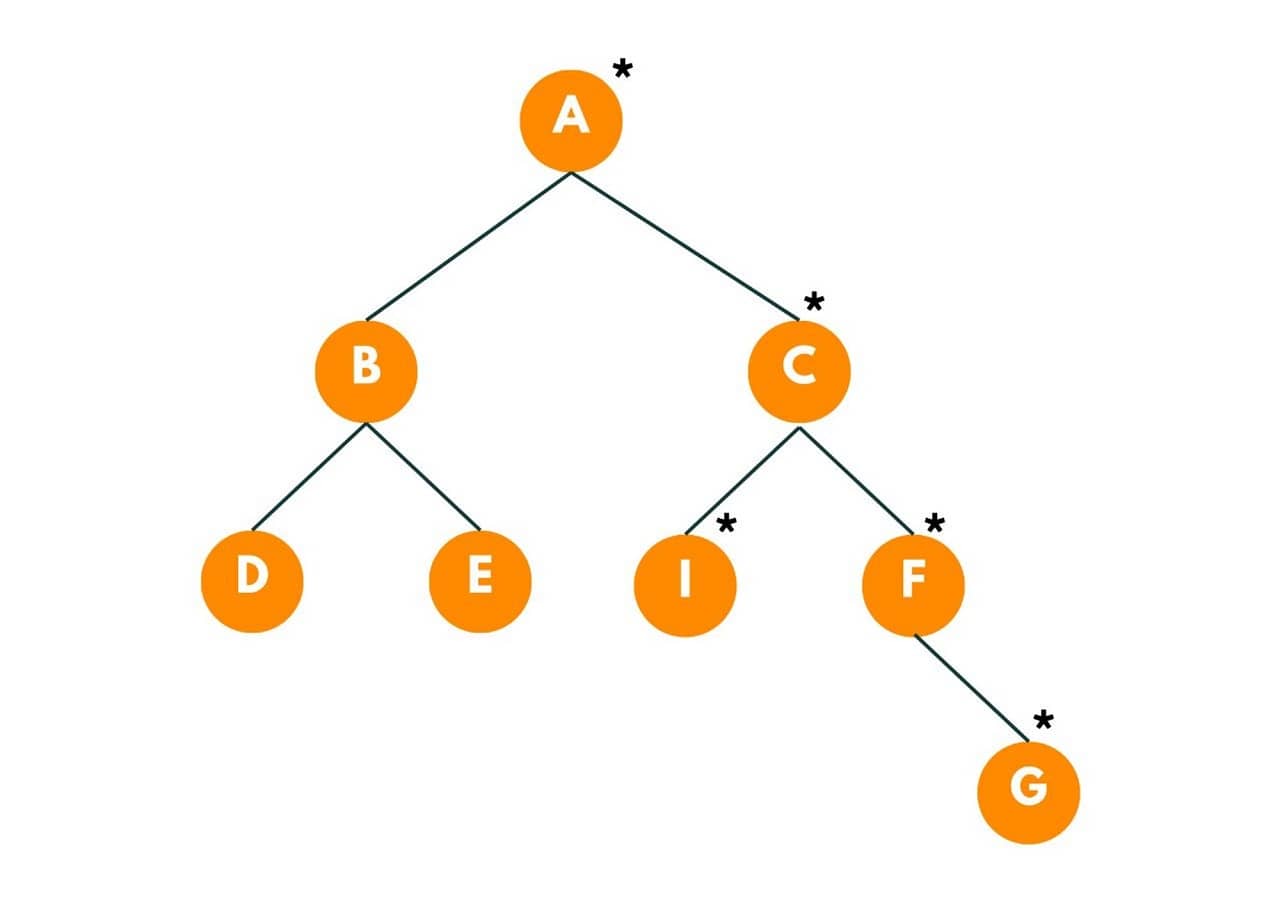
Now fire will move towards the neighbors of A, i.e., B. Time = 3 seconds.

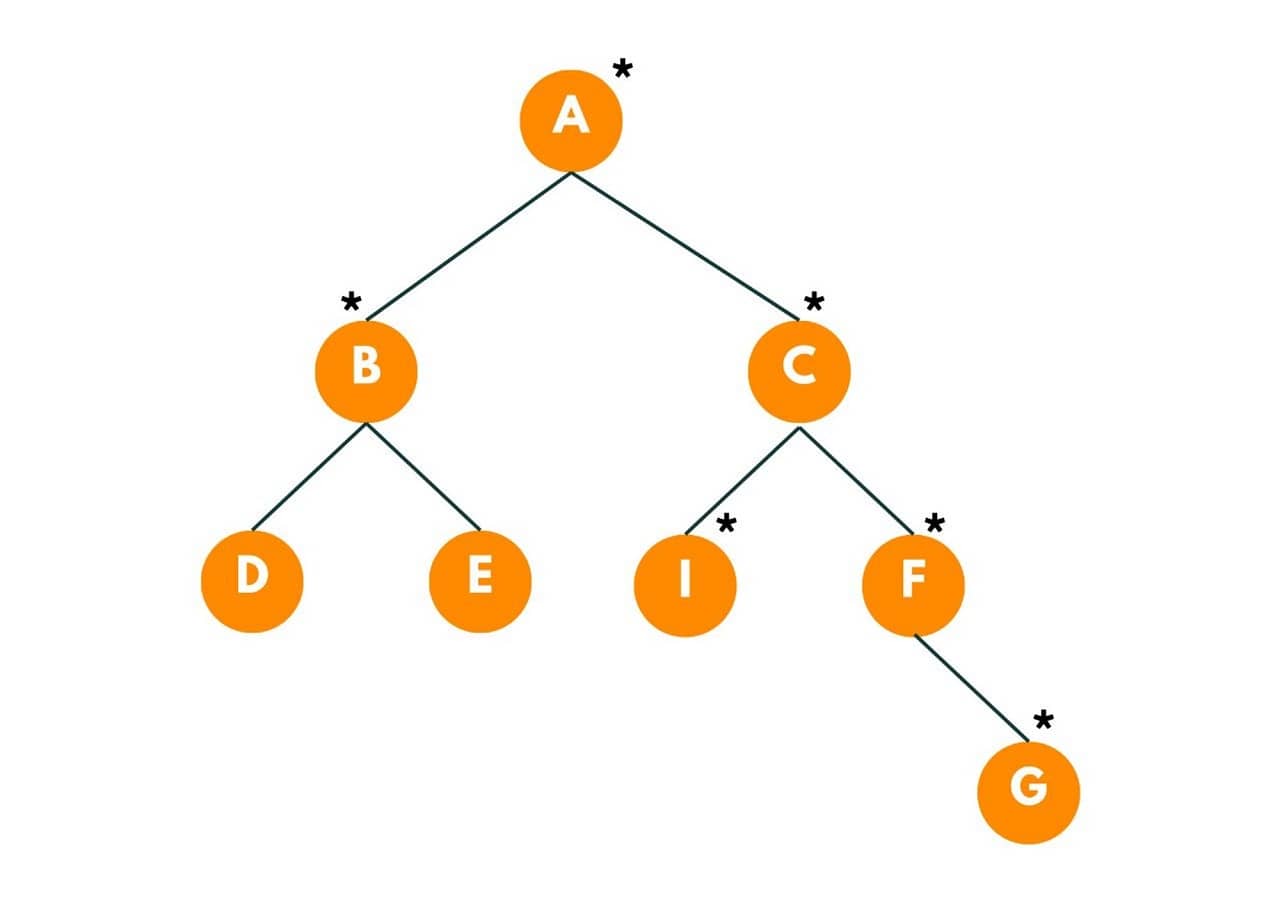
Now D and E will be burnt as fire move towards neighbors of B. Time = 4 seconds.

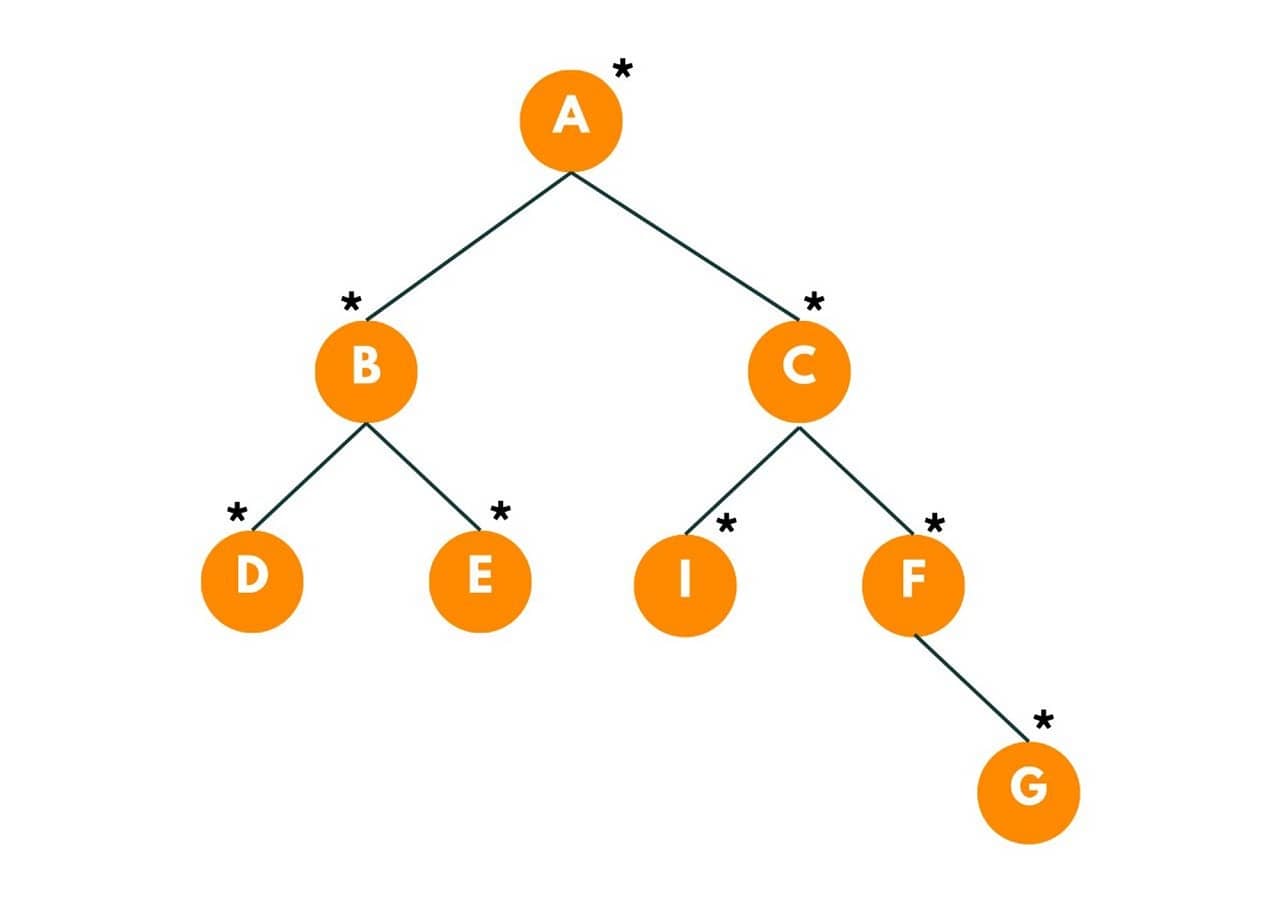
So the total minimum time taken to burn the binary tree is 4 seconds.

So here we are going to use a recursive approach.

First, we try to find out the time taken by fire to spread from the given node to the nodes in its left and right subtree. So we move toward its left subtree first and increase the time count by one and similarly, we explore the right subtree of the given target. We keep doing so unless we have our call stack empty.

Now we need to find out the time taken to burn the upper half tree. To do so we use the concept of blocker node. In the above tree, F was the target, so in order to burn the upper tree, fire spreads from F to C and then to I.

But can this fire be again spread to F? Obviously not, so we use F as the blocker node here, implying that if the fire is spread from child to parent, it can't again spread towards the child.

So, We use the concept of the node to root path in order to travel upwards using the concept of blocker node.

Minimum Time Taken to Burn the Binary Tree

Here is an algorithm to find the minimum time take for burning a binary tree:

1. We create a static variable called 'minTime' which would contain the minimum time to burn the whole binary tree.
2. Then we create a function called 'burningTree()' that has two arguments - the root node and the target node (or the node that has been set on fire).
3. We make a call to a function called 'nodeTorootPath(root, FireNode)' that would do the task of traveling to fireNode . It is basically the node to root path finding function.
4. In this function, we will make a call to the left and the right subtree and we are going to find out the value passed to this function. In Short, we find the path from root to the fireNode.
5. After we find the fireNode, we move to call another function  'burnTree()' that would find the minimum time taken to burn the tree. Initially we pass, time as 0, root node as fireNode and a blocker node as null.

Here is the Java code to implement this algorithm:

public static int minTime = 0;
  
  public static void burnTree(TreeNode root, int time , TreeNode block){
      //base case
      if(root == null || root == block) return;
      
      //updating the time 
      minTime = Math.min(minTime, time);
      
      //spreading the fire to left and right subtree.
      burntTree(root.left, time + 1, block);
      burntTree(root.right, time + 1, block);
  } 
  public static int burningTree(TreeNode root, int fireNode) {
      
      minTime = 0;
      
      //this function would do the task of traveling to fireNode and start burning the whole tree 
      burnTree(root, fireNode);
      
      //at the end we return the minimum time taken to burn the binary tree.
      return minTime;

  }
  //this function will be similar to find node to root path.
  public static nodeToRootPath(TreeNode root, int fireNode){
      
      //base case1 when we reach till the last of tree.
      if(root == null) return -1;
      
      //base case2 when we found the fireNode
      if(root.val == fireNode) {
          //we call a another function named burnTree that would find the minimum time taken to burn the tree.
          burnTree(root, 0, null);
          return 1;
      }
      
      //left time
      int lt = burnTree(root.left, fireNode);
      if(lt != -1){
          burnTree(root, lt, root.left);
          return lt + 1;
      }
      
      //right time 
      int rt = burnTree(root.right, fireNode);
      if(rt != -1){
          burnTree(root, rt, root.right);
          return rt + 1;
      }
      
      //we return -1 if we don't find the fireNode
      return -1;
  }

Time & Space Complexity  

The time complexity of the provided code depends on the size of the binary tree. The time complexity of visiting every node in a binary tree of size n is O(n), and the time complexity of calling the burnTree function on each node in the tree is also O(n).

Therefore, the overall time complexity of the above code is O(n^2). The burningTree function first calls the burnTree function, which visits every node in the binary tree once. Then, for each node, it calls the burnTree function on its left and right subtrees, which can also visit every node in those subtrees once. The total number of nodes visited is proportional to the size of the binary tree.

The space complexity of the provided code is O(1) because it only uses a constant amount of space, regardless of the size of the input. The space used is independent of the size of the input list, as it only uses a fixed number of variables to keep track of the values found so far.

One more interesting problem to solve for new programmers is how to invert a binary tree, which you can also try.

Conclusion

This Burning Binary Tree problem requires a good understanding of binary trees and recursion. While the algorithm presented here works for a specific scenario, there may be variations of the problem that require different approaches. If you still have any doubts, our Data Structures Tutors are available 24/7 to help you anytime.