Deep in the roots of a binary tree lies a crucial node, known as the lowest common ancestor, holding the key to unlocking a myriad of computational puzzles. Let's delve into the fascinating world of binary trees and explore the puzzle of finding the LCS.
Lowest Common Ancestor of a Binary Tree
Before we delve into the concept of the lowest common ancestor of a binary tree, let's first understand what a binary tree is. A binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. The first node in a binary tree is called the root node. The nodes that do not have any children are referred to as leaf nodes.
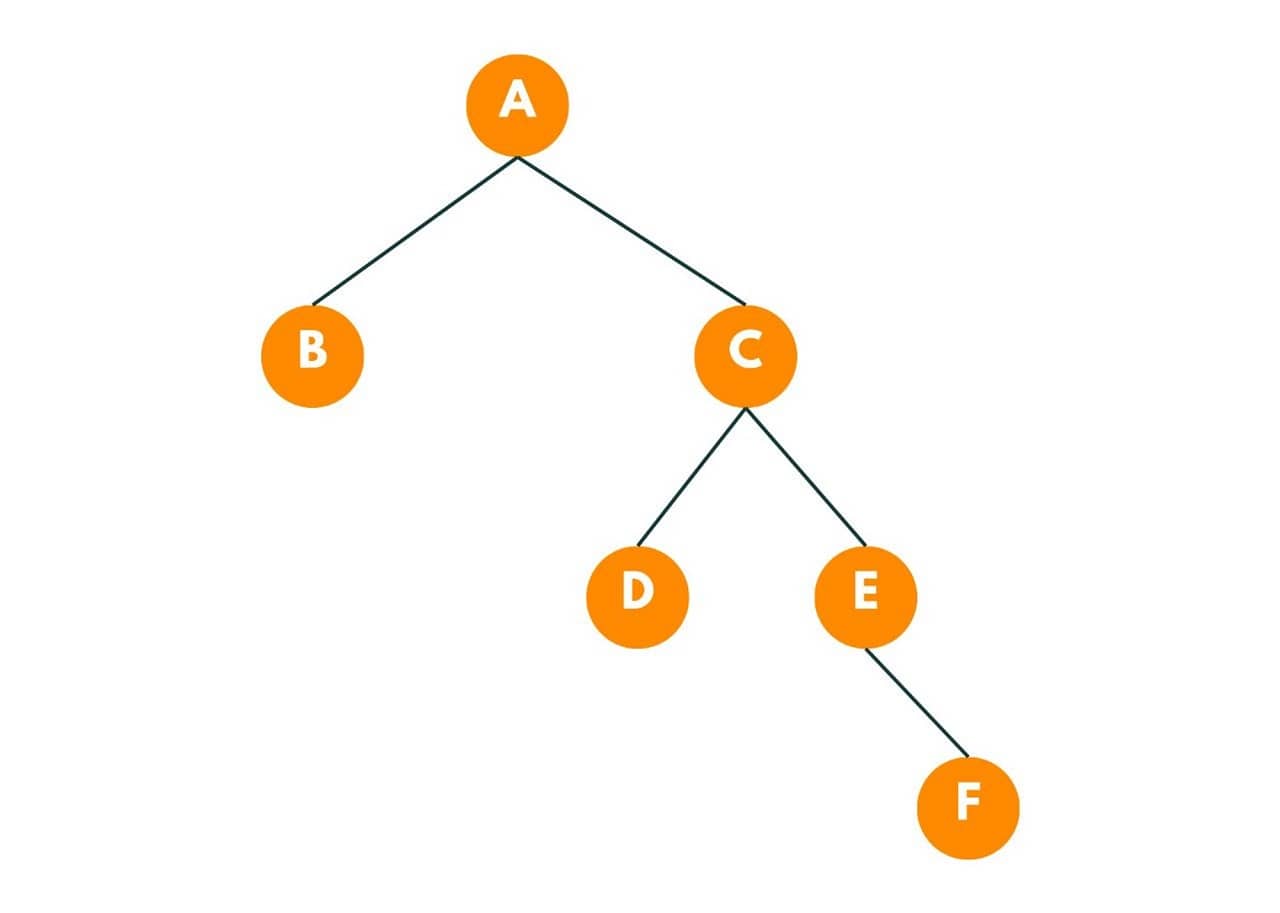
The above is a representation of a binary tree. Here A is the root node and B, D, and F are the leaf nodes.
The lowest common ancestor of a binary tree is the lowest node that has both the given nodes as descendants. In other words, it is the node that is furthest from the root node but still has both the given nodes as descendants.
Let's see an example:
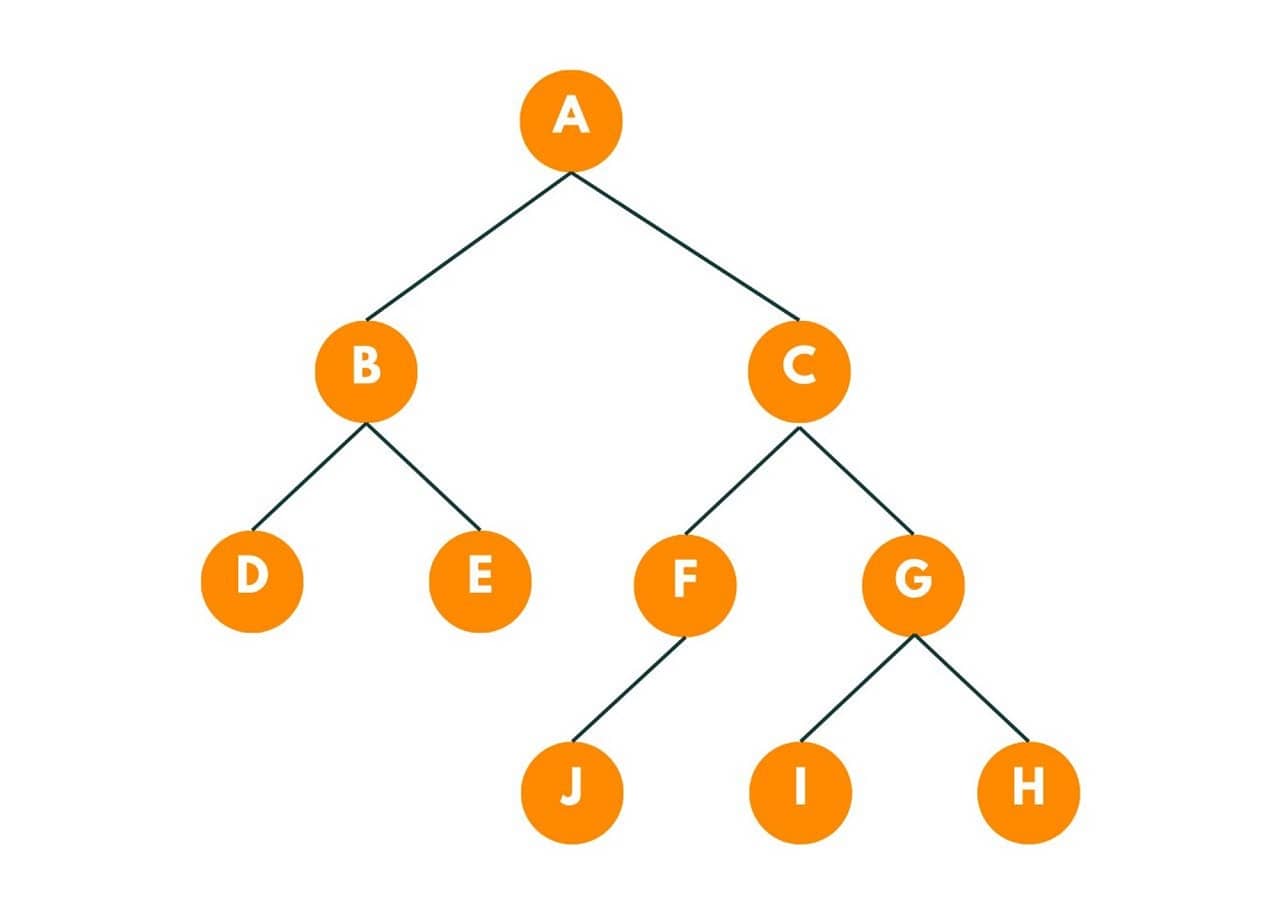
In the above binary tree, the lowest common ancestor of Node I and Node J is C, as it is the lowest node that has both of the given nodes.
Now, we know what it is, let's declare the problem statement: "Given a binary tree and two nodes, n1, and n2, we need to find the lowest common ancestor of these nodes with their values as n1 and n2. If no lowest common ancestor exists, return NULL. "
How to Find LCS in a Binary Tree?
If we need to find the lowest common ancestor, we would go to each parent node and will check if that node exists in the left subtree and same we will check for the right subtree. If both the nodes exist in the left and right subtree respectively, we return the parent node as the lowest common ancestor.
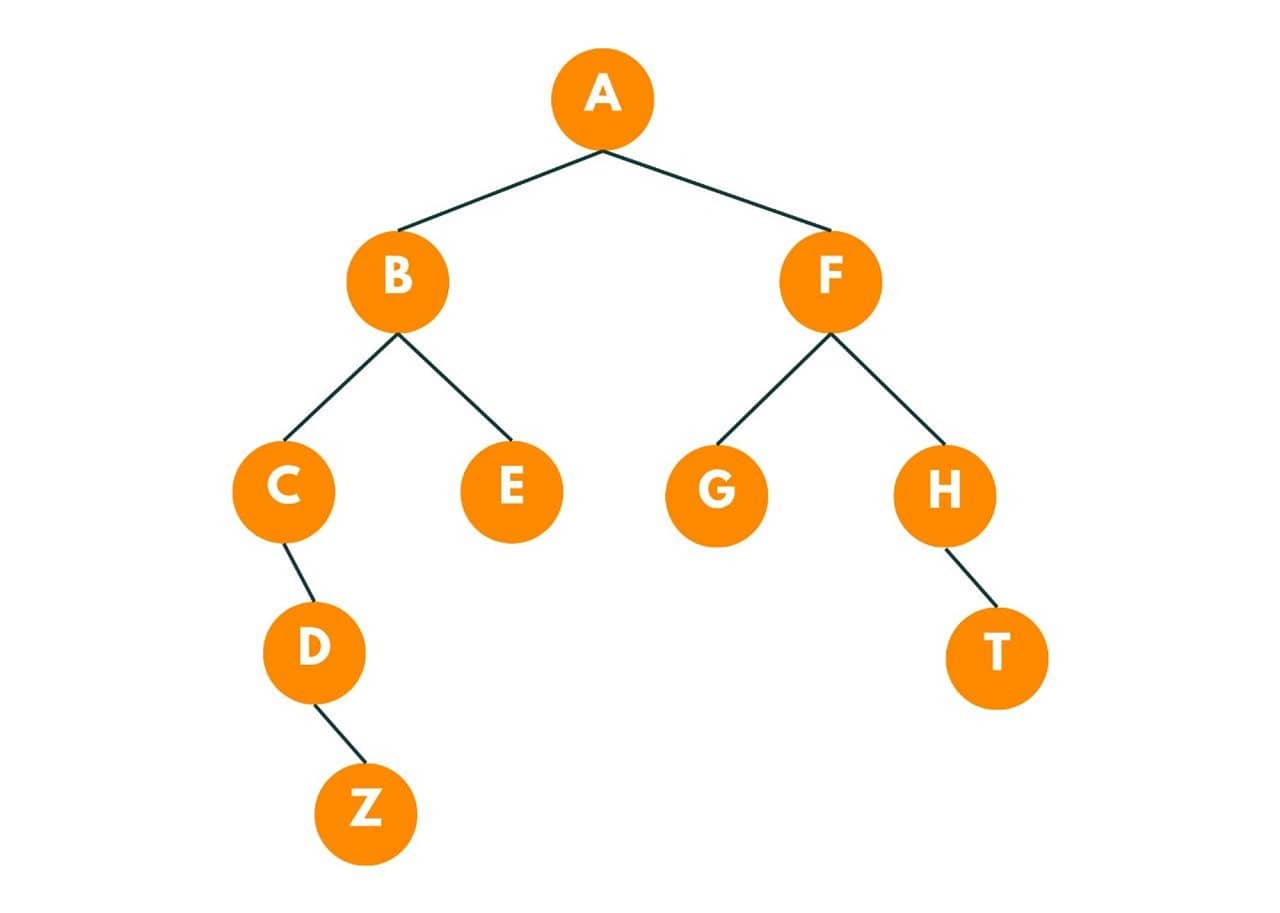
In the given image, we need to find out the lowest common ancestor of node 'D' and node 'E'.
So for each parent node, we check the right and left sub-tree, if both node exists, we return the parent node. Node 'B' has node 'D' in the left subtree and node 'E' in the right subtree, so the lowest common ancestor here is node 'B'.
Here is the algorithm to find the Lowest Common Ancestor in a Binary Tree:
- We create a global variable, LCA, containing our answer.
- We create three boolean variables, namely, self (checks if the parent node is equal to the given node), right(checks whether a node is present in the right subtree), and left(checks whether a node is present in the left subtree).
- First, we check if the node is equal to NULL, which implies, no child exists, we return false.
- Then we check if the value of the node is equal to one of the given data.
- Then by recursion, we call the same function by passing the left subtree as the current node.
- After checking the left subtree, we call the same function by passing the right subtree as the current node.
- We mark the current node as true if we get the following situation:
- left and right variables are true.
- left and self variables are true.
- right and self variables are true.
- At the end we return any of these three variables which is true.
- After passing the call to the left and right subtree, we check the base condition as - when the variable LCA is not null, that implies, already we have found the lowest common ancestor, so we return true.
Note that this algorithm also handles the case when one of the given nodes doesn't exist in the tree.
Here is the Java code to find LCS in a binary tree:
// taking the result as LCA private static TreeNode LCA = null; //this function returns true if the lowest common ancestor is found public static boolean LCA_DFS(TreeNode node, int p, int q) { //if node doesn't exist return false; if(node == null) return false; //check if the current node is equal to given data or not. boolean self = (node.val == p || node.val == q); //check if the left subtree of current node contains one of the given data or not. boolean left = LCA_DFS(node.left, p, q); // if we found both the nodes in the left subtree, we return true if(LCA != null) return true; //check if the right subtree of current node contains one of the given data or not. boolean right = LCA_DFS(node.right, p, q); // if we found both the nodes in the right subtree, we return true if(LCA != null) return true; //checking the scenarios where the current node can be the given data. if((left && right) || (left && self) || (right && self)){ LCA = node; } //at the end, we return the variable which is true. return self ||left || right; } public static TreeNode lowestCommonAncestor(TreeNode node, int p, int q) { LCA_DFS(node, p, q); return LCA; }
Testing Algorithm to Find Lowest Common Ancestor
Here is the example we are going to take:
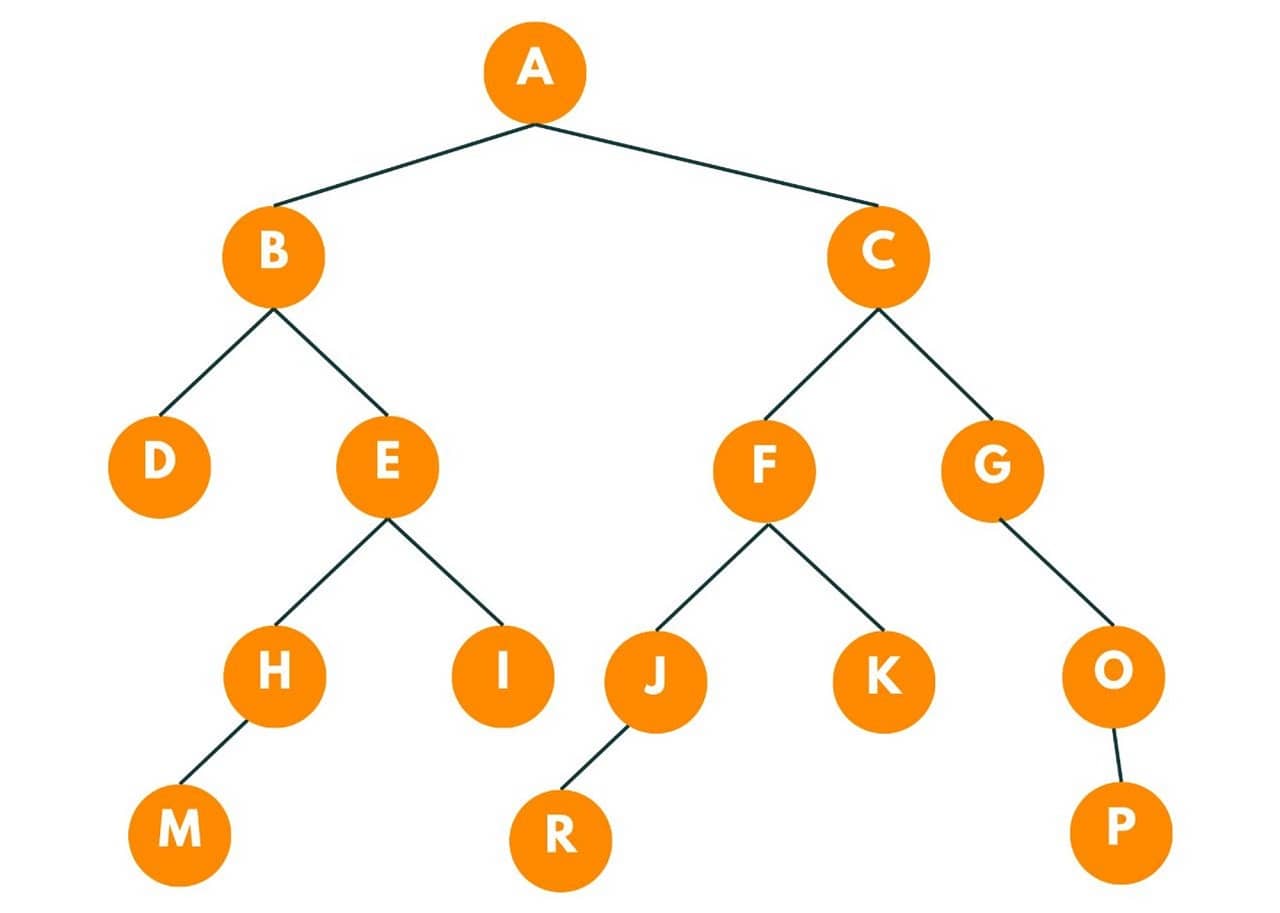
To find the lowest common ancestor of node 'E' and node 'F'.
At each node we reach, we ask three questions from that node:
- Is that node equal to the given data?
- Does one of the given nodes exist in its left subtree?
- Does one of the given nodes exist in its right subtree?
1) We start from the root node and we keep three variables self, left and right corresponding to the questions. So as the root node is not equal to the given data, we move to its left.
The stack contains the current node and the variable we are shifting to - self, left, or right.
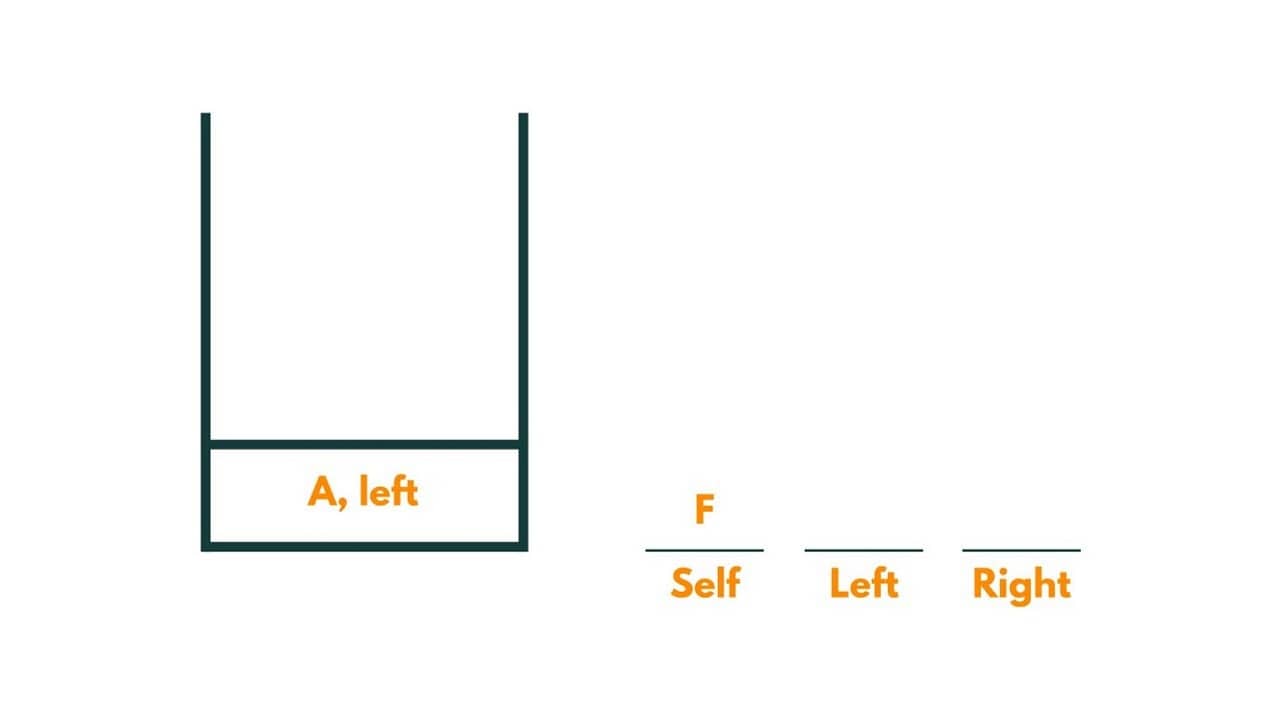
2) The current node is B. As B is not equal to the data, we move to its left.
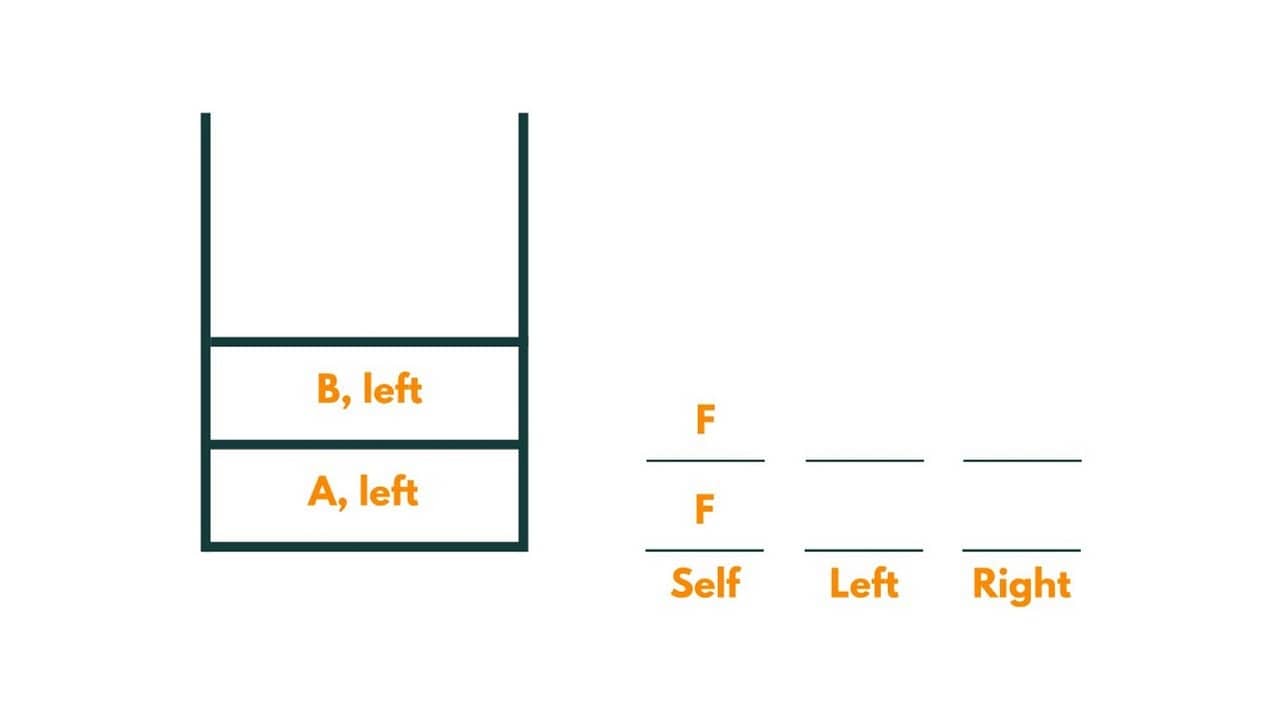
3) The current node is D. As D is not equal to the data, we move to its left.
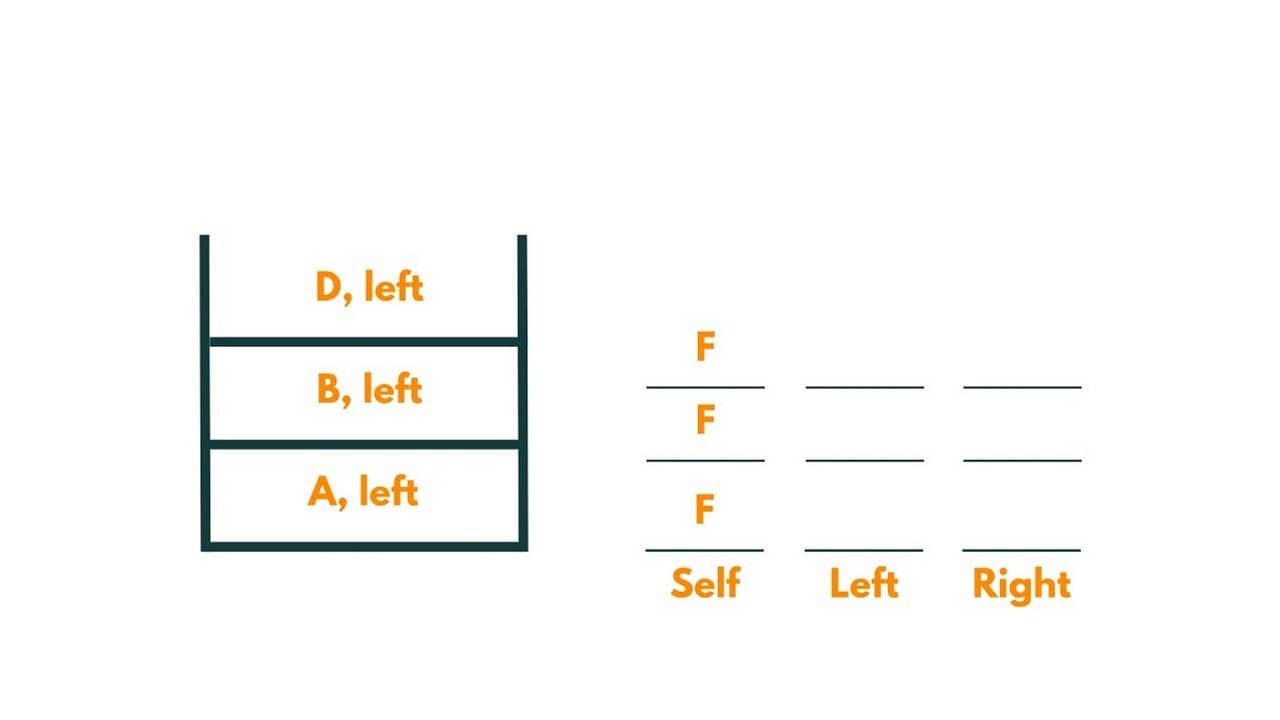
As D has no child in the left subtree, it returns false and we move to the right subtree of D. It again returns false, as no child is present in the right subtree.
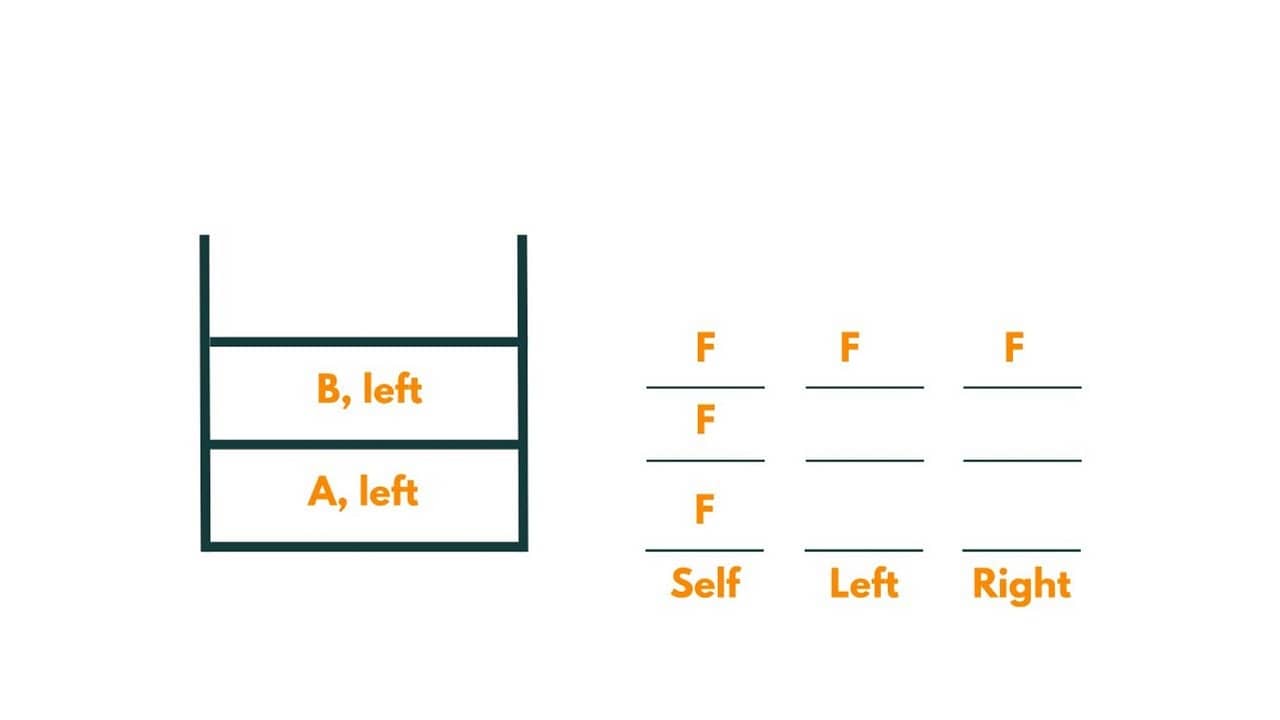
4) Now we move to the right subtree of B, i.e., node E. As node E is equal to the given data, it returns true. B further returns true to A.
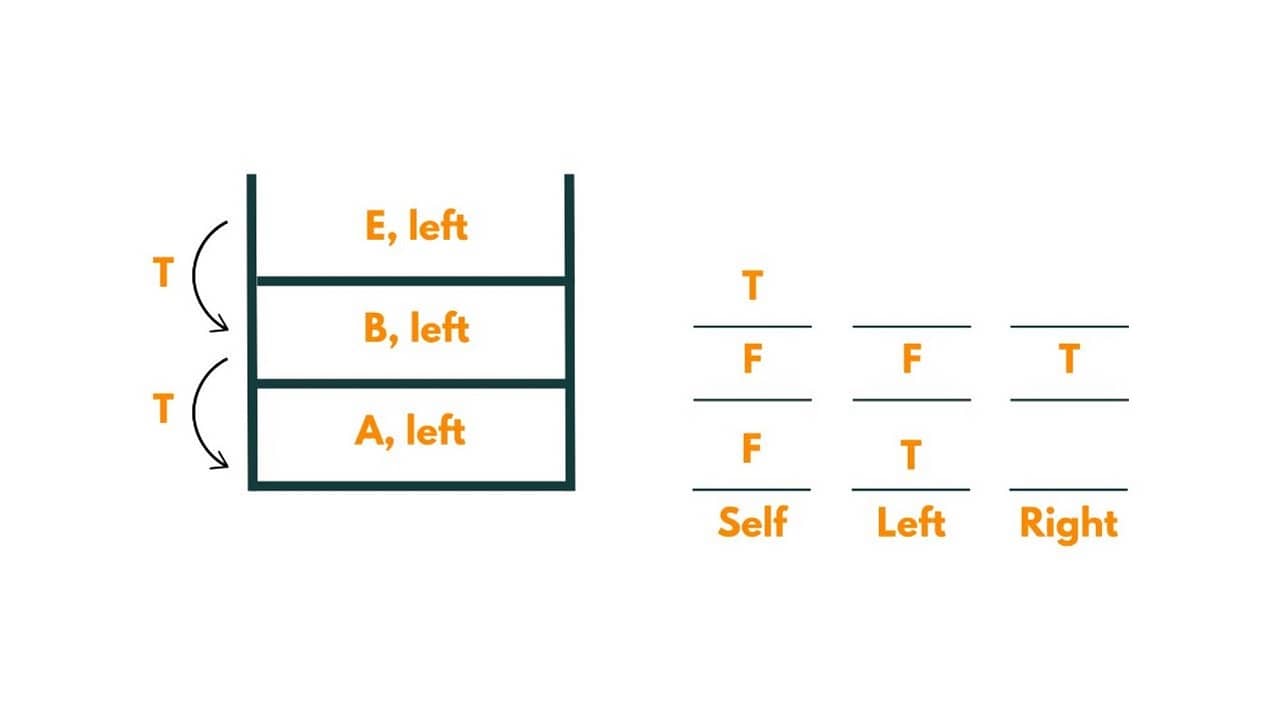
5) Then we move to the right subtree of A, i.e., node C.
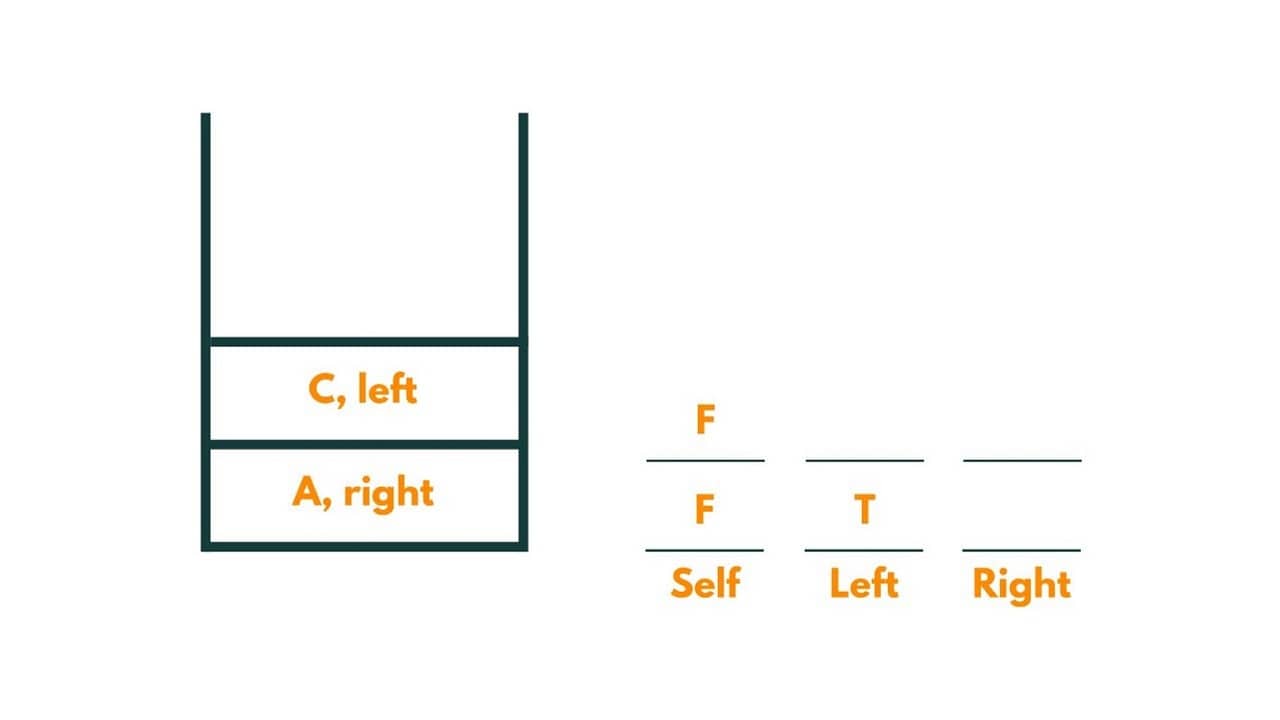
6) As it is not equal to the given data, we move to its left,i.e., node F.
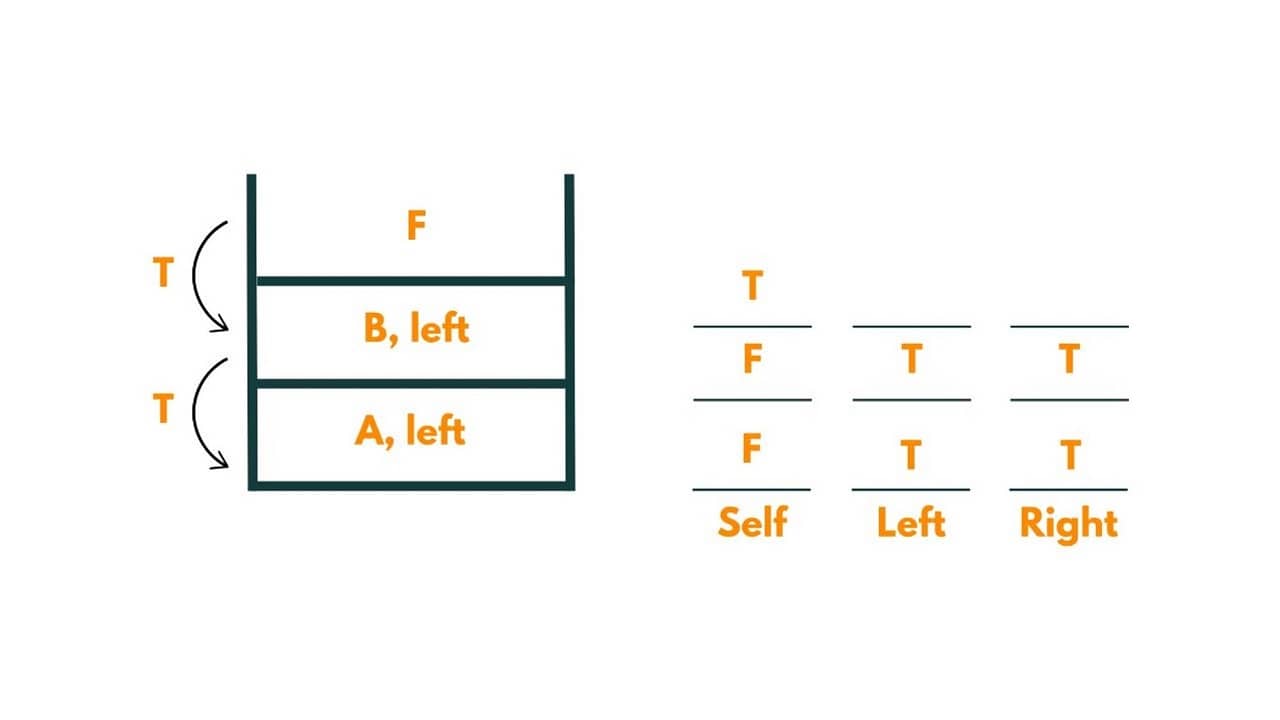
As node F is equal to the given data, it returns true. Further node C returns true to A.
And we return the lowest common ancestor as 'A'.
Space & Time Complexity
The space complexity to find the lowest common ancestor would be O(H) where H is the height of the binary tree. This is because the recursive calls to LCA_DFS function will be pushed onto the call stack and the maximum number of recursive calls on the call stack would be equal to the height of the binary tree.
The above code traverses through all the nodes of the binary tree once and performs constant time operations at each node. The LCA_DFS function is called on each node of the binary tree, and the total nodes visited in the worst-case scenario would be equal to the number of all the nodes in the binary tree, say, N. So the total time complexity comes out to be O(N).
Also, learn how to find the Height of the Binary Tree here.
Conclusion
Overall, the LCA of a binary tree is a fundamental concept in computer science with a wide range of applications such as networking, graph theory, and genetics. It's worth noting that there are various algorithms available to find the LCA of the binary tree, each with its own time and space complexity trade-offs. Therefore, it is essential to choose the right algorithm depending on the specific use case.








