The Longest Palindromic Substring is a classic problem of dynamic programming with strings. This question is of a certain type and if you understand it, you can solve many similar problems. In this blog, we will explore different approaches to solving the Longest Palindromic Substring problem, ranging from brute-force methods to more optimized algorithms.
What is Longest Palindromic Substring?
In the Longest Palindromic Substring problem, we have to find the longest contiguous substring within a string that is a palindrome. The substring will be called a palindrome when characters in it read the same forwards and backward.
First, we would be given a string and we have to return the length longest palindromic substring. For example, the substrings of the string "accbc" are: a, ac, acc, accb, accbc, c, cc, ccb, ccbc, c, cb, cbc, b, bc, c. The palindromic substrings are - a, c, cc, cbc, b. The longest palindromic substring is cbc. So, we return 3.
In the realm of computer science, there are multiple approaches to solving this problem. Let's discuss them one by one.
Brute Force Approach
The easiest approach that can we think of would be exploring all the substrings and checking if they are palindromic or not. It is a straightforward but not efficient method for larger strings due to its high time complexity.
Here is the code in Java to implement Brute Force Approach:
public class LongestPalindromicSubstring { public static void main(String[] args) { String s= "abccbc"; int maxLen = findLongestPalindromicSubstring(s); System.out.println("The longest palindromic substring is of length : " + maxLen); } public static int findLongestPalindromicSubstring(String s) { int maxLen = Integer.MIN_VALUE; String longestSubstring = ""; // taking out each substring for (int i = 0; i < s.length(); i++) { for(int j = i + 1; j <= s.length(); j++) { String subString = s.substring(i, j); //checking if the substring is palindromic or not boolean isPalindromic = checkPalindrome(subString); //if substring is palindromic, we compare its length with maxSubstring length. if(isPalindromic) { if(maxLen < subString.length()) { maxLen = subString.length(); longestSubstring = subString; } } } } return maxLen; } public static boolean checkPalindrome(String s) { int i = 0; int j = s.length() - 1; while( i < j) { char ch1 = s.charAt(i); char ch2 = s.charAt(j); if(ch1 != ch2) { return false; } i++; j--; } return true; } }
Output:
The longest palindromic substring is of length : 4
For each character at the i-th position, we iterate over i+, i+2---n i.e. length of the substring. For each substring, we check if it is palindromic or not which is done in O(LogN) time. So, the total time complexity comes out to be O(N^2 LogN). As no extra space has been used, the space complexity is O(1).
Optimized Approach using Dynamic Programming
Here are the steps to solving the Longest Palindromic Substring with an Optimized approach:
We create a 2D array of size-string.length() * string.length(). Say, taking the example of string abccbc.
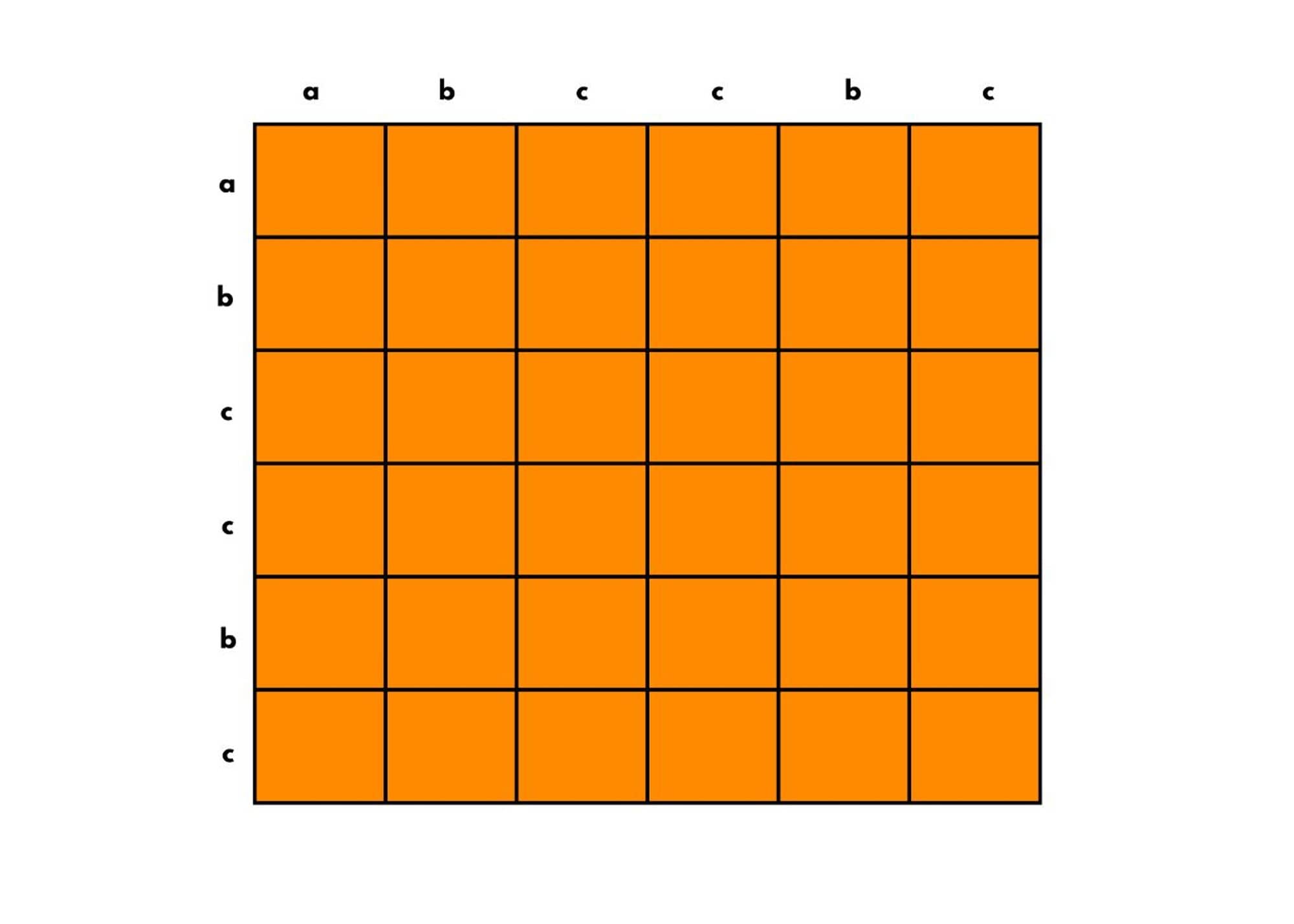
Each of these cells is representing the substring that has been assigned to it that starts from the corresponding row element and ends at the corresponding column element.
So the cell (0,0) says that the substring will start from 'a' and ends at 'a', so we fill the box as a. The cell (0,1) tells that it starts at a and ends at b in the string, so we put "ab" in that cell. Likewise, we fill each cell.
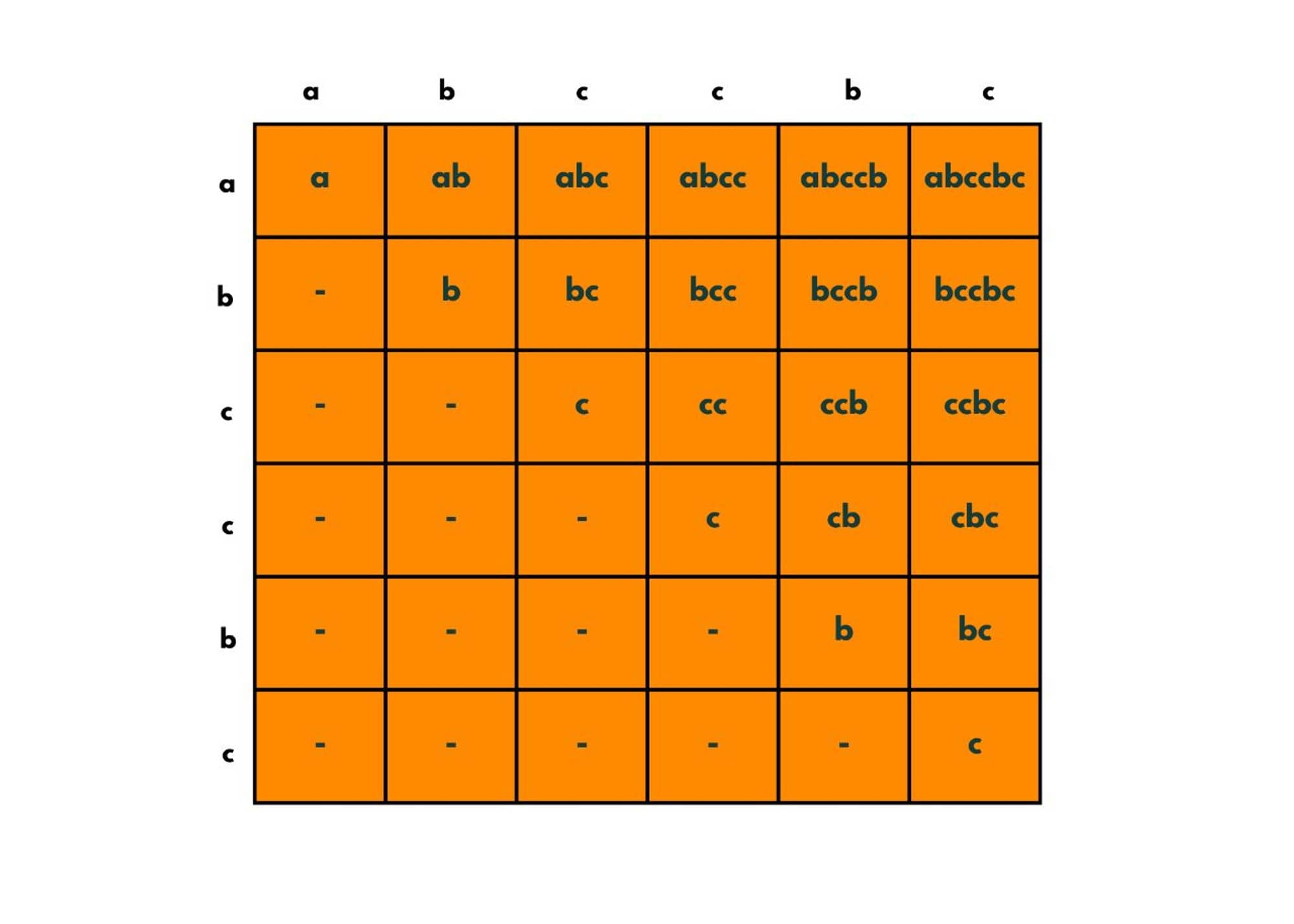
The cells in the lower triangle are not filled as their starting element occurs after the ending element. So a string can't be formed.
Here, from this image, we can notice some important points. The diagonal starting from the cell (0,0) has all the substrings of length 1. The diagonal across the cell (0,1) has all substrings of length 2 and so on.
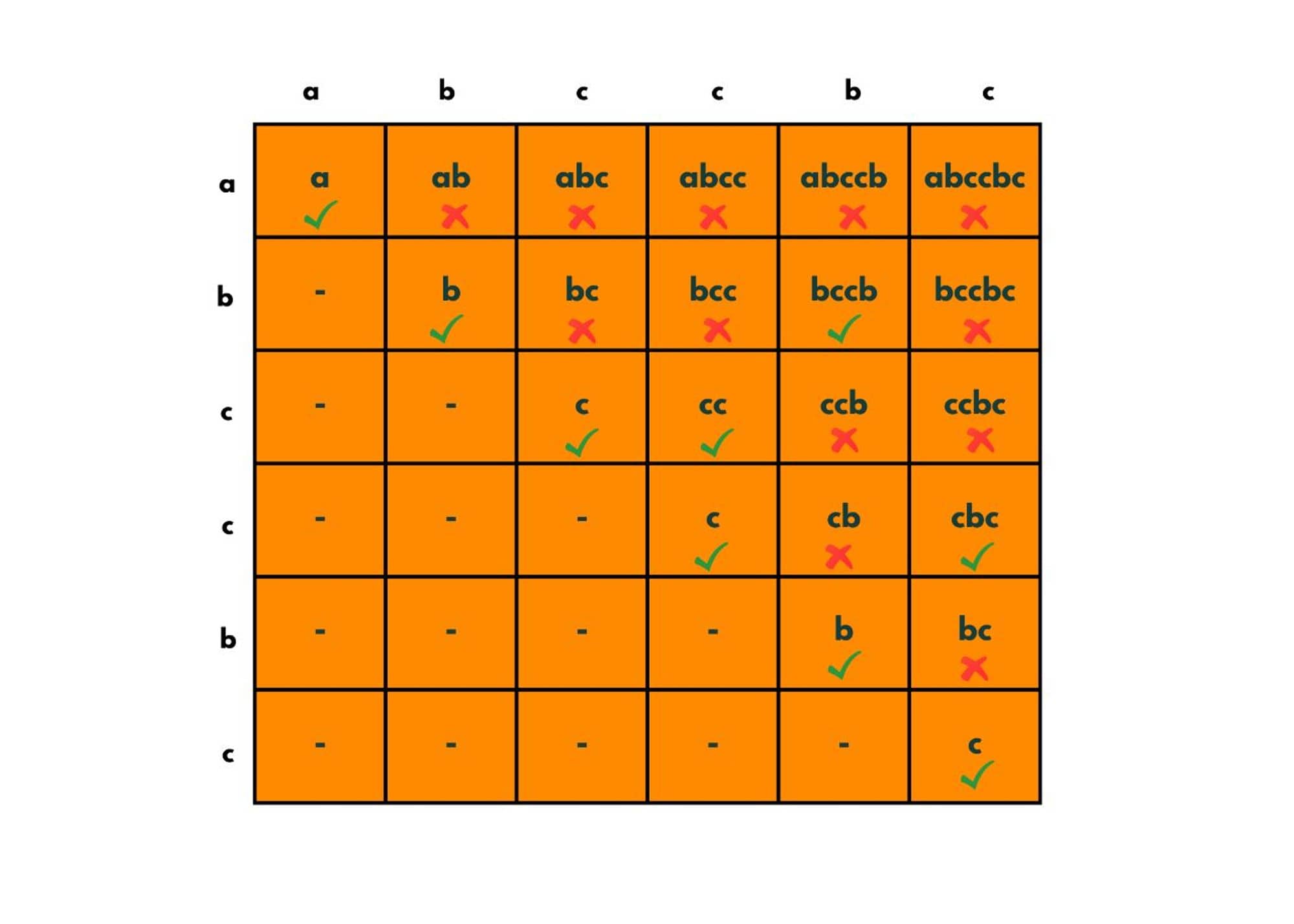
All the substrings across the 0-th diagonal are palindromic. In 1st diagonal, all the substrings of the same characters are palindromic as they are of size = 2.
In the diagonals 2nd, 3rd, 4th, and 5th we check their extremes and the middle if the characters are the same or not. So we place truly in the cells where we found palindromic substrings.
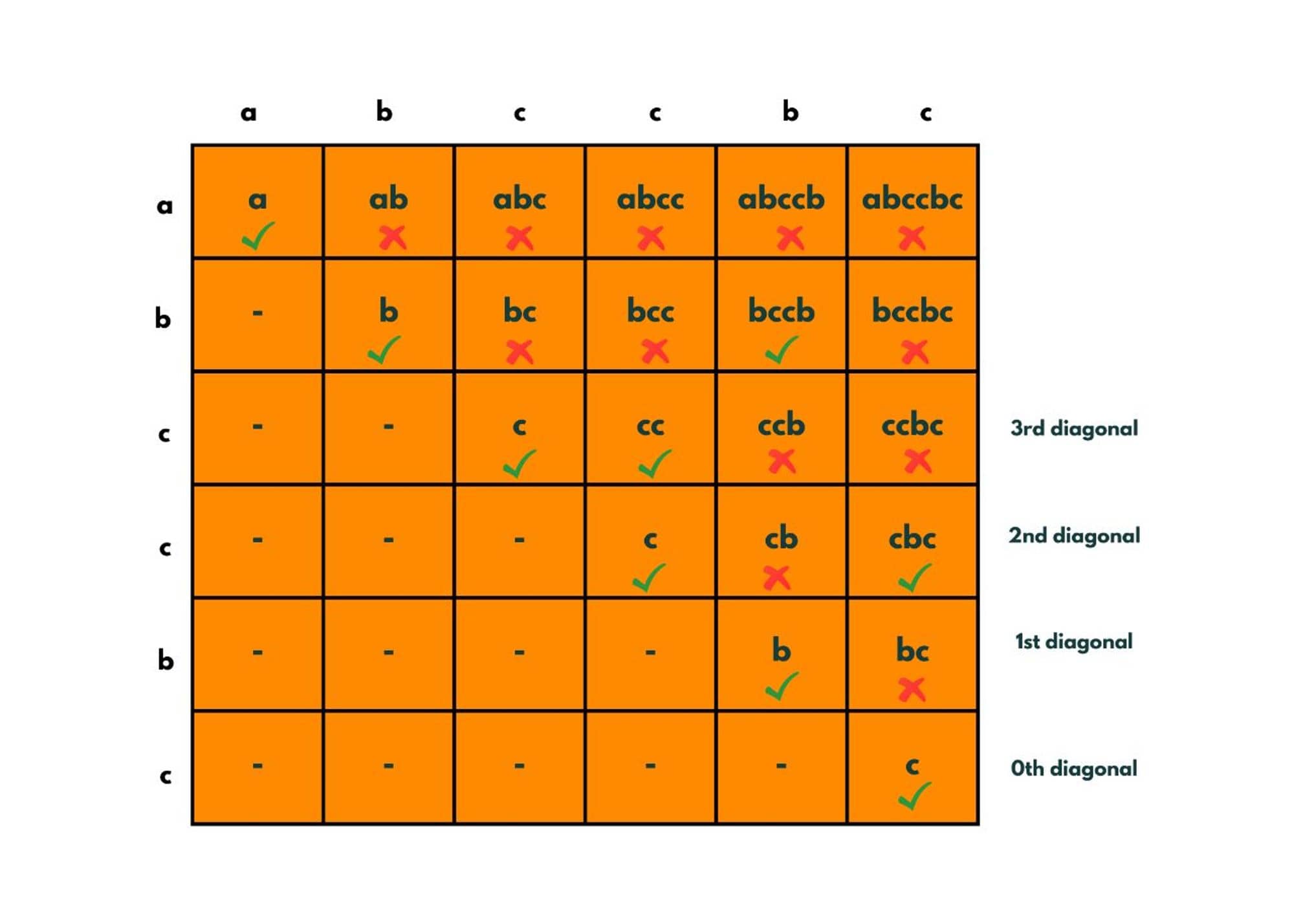
Now the greatest diagonal having true will be the answer. So we return the answer as diagonal + 1. So here, we have the 3rd diagonal to have the greatest length of the palindromic substring. So we return the answer as diagonal + 1.
The following is the Java Code for the Optimized Approach to solve this problem:
public class LongestPalindromicSubstring { public static void main(String[] args) { String s= "abccbc"; LongestPalindromicSubstring(s); } public static void LongestPalindromicSubstring(String str) { // creating a boolean dp array boolean[][]dp = new boolean[str.length()][str.length()]; //initializing maximum length of palindromic substring int maxLen = 0; //filling the 2D array with the following gaps. for (int gap = 0; gap < str.length(); gap++) { // for each gap we fill the dp array as starting point as i and ending point as gap. for (int i = 0, j = gap; j < str.length(); i++, j++) { // if gap is 0 , this implies we are at 0th diagonal, where all substrings are palindromes. if (gap == 0) { dp[i][j] = true; } else if (gap == 1) { //checking if both the characters are equal or not. if (str.charAt(i) == str.charAt(j)) { dp[i][j] = true; } else { dp[i][j] = false; } } else { //checking the middle and extreme parts of substring if they are equal or npt . if (str.charAt(i) == str.charAt(j) && dp[i + 1][j - 1] == true) { dp[i][j] = true; } else { dp[i][j] = false; } } //storing the maximum palindromic substring length. if (dp[i][j]) { maxLen = gap + 1; } } } System.out.println("The maximum length of palindromic substring is : " + maxLen); } }
Output:
The maximum length of palindromic substring is : 4
As we traverse over the 2-D array, the time complexity comes out to be O(N^2). And as we take extra space for creating a 2-D dp array, the time complexity comes out to be O(N^2).
Check other Dynamic Programming problems to learn and practice more.
Conclusion
This Longest Palindromic Substring problem is important not only from an interview point of view but also for building concepts. We discussed both the Brute Force approach and the Optimized approach using Dynamic Programming.








