Ever wondered how a computer playing as a chess player improves its algorithm to defeat you in the game? In this article, we will learn about the Knight's Tour Problem, the various ways to solve it along with their time and space complexities. So, let's get started!
What is Knight's Tour Problem?
Just for a reminder, the knight is a piece in chess that usually looks like a horse and moves in an L-shaped pattern. This means it will first move two squares in one direction and then one square in a perpendicular direction.
The Knight's Tour problem is about finding a sequence of moves for the knight on a chessboard such that it visits every square on the board exactly one time. It is a type of Hamiltonian path problem in graph theory, where the squares represent the vertices and the knight's moves represent the edges of the graph.
This problem has fascinated many mathematicians for centuries, but the solutions they found were very difficult. The simple solution will be to find every conceivable configuration and selecting the best one is one technique to solve this problem. But that will take a load of time.
One popular solution to solve the Knight's tour problem is Warnsdorff's rule, which involves choosing the next move that leads to a square with the fewest available moves. There is also a backtracking approach.
But first moving to all that, let's take a quick understanding of the Hamiltonian path problem.
Hamiltonian Path Problem
The Hamiltonian path problem is a well-known problem in graph theory that asks whether a given graph contains a path that visits every vertex exactly once.
A path that visits every vertex exactly once is called a Hamiltonian path, and a graph that contains a Hamiltonian path is called a Hamiltonian graph.
Let's take an example of the Hamiltonian path problem. Suppose we have a graph with five vertices and the following edges:
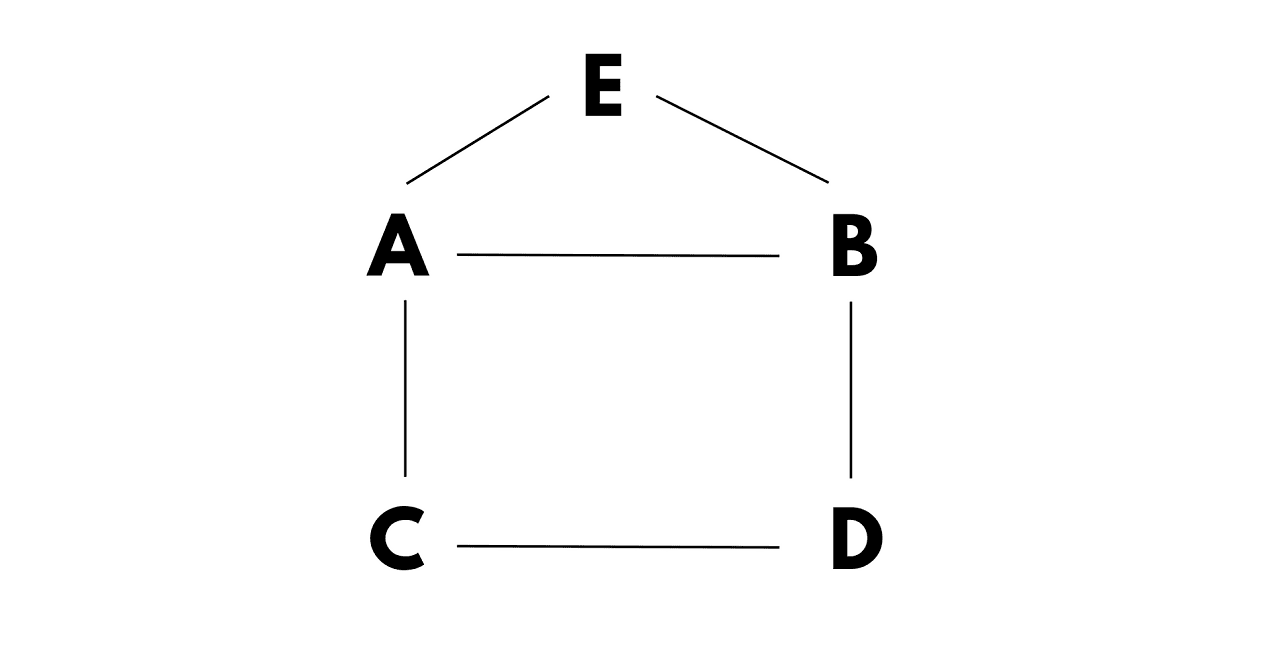
This graph can be represented as:
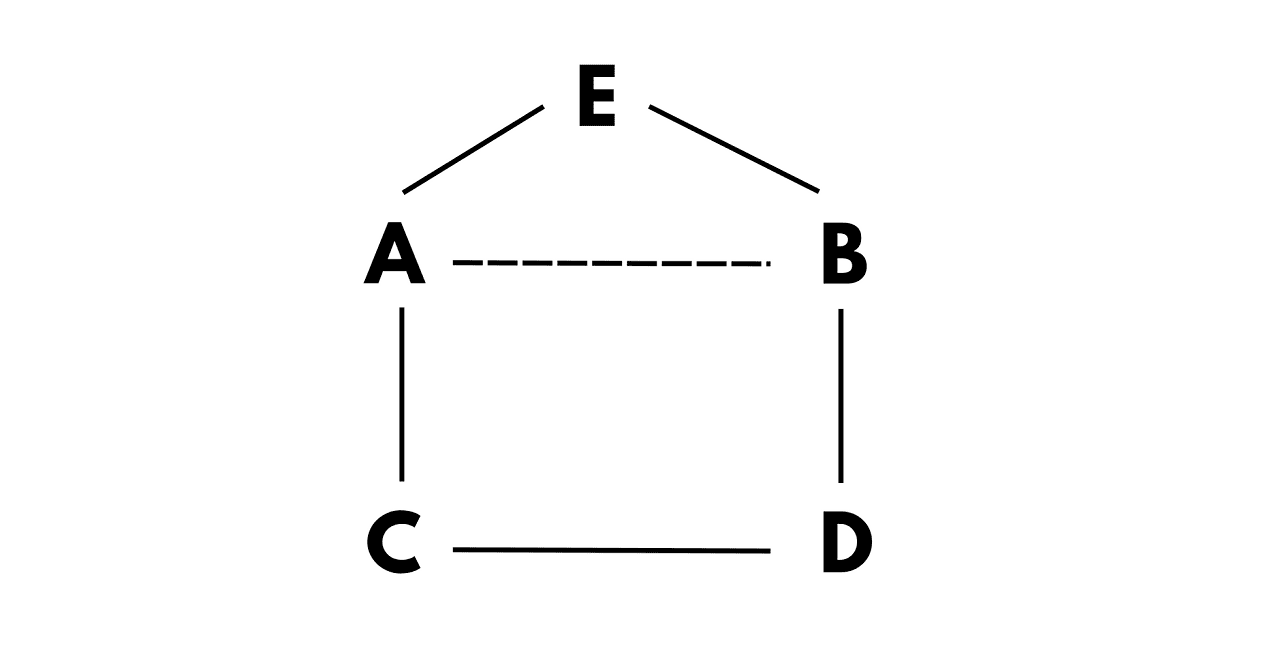
Knight's Tour Backtracking Algorithm
The backtracking algorithm works by exploring all possible moves for the knight, starting from a given square, and backtracking to try different moves if it reaches a dead end.
Here's the basic outline of the backtracking algorithm to solve the Knight's tour problem:
- Choose a starting square for the knight on the chessboard.
- Mark the starting square as visited.
- For each valid move from the current square, make the move and recursively repeat the process for the new square.
- If all squares on the chessboard have been visited, we have found a solution. Otherwise, undo the last move and try a different move.
- If all moves have been tried from the current square and we have not found a solution, backtrack to the previous square and try a different move from there.
- If we have backtracked to the starting square and tried all possible moves without finding a solution, there is no solution to the problem.
We have given the full C++ program for Backtracking Algorithm to solve Knight's Tour Problem below:
#include #include using namespace std; const int N = 8; int board[N][N]; int moveCount = 0; vector<pair<int, int>> validMoves(int row, int col) { vector<pair<int, int>> moves; int rowMoves[] = {-2, -1, 1, 2, 2, 1, -1, -2}; int colMoves[] = {1, 2, 2, 1, -1, -2, -2, -1}; for (int i = 0; i < 8; i++) { int newRow = row + rowMoves[i]; int newCol = col + colMoves[i]; if (newRow >= 0 && newRow < N && newCol >= 0 && newCol < N && board[newRow][newCol] == 0) { moves.push_back(make_pair(newRow, newCol)); } } return moves; } bool solve(int row, int col, int moveNum) { board[row][col] = moveNum; moveCount++; if (moveNum == N*N) { return true; } vector<pair<int, int>> moves = validMoves(row, col); for (pair<int, int> move : moves) { int newRow = move.first; int newCol = move.second; if (solve(newRow, newCol, moveNum+1)) { return true; } } board[row][col] = 0; moveCount--; return false; } int main() { int startRow = 0, startCol = 0; solve(startRow, startCol, 1); cout << "Number of moves: " << moveCount << endl; for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { cout << board[i][j] << " "; } cout << endl; } return 0; }
Output:
Number of moves: 64 1 38 55 34 3 36 19 22 54 47 2 37 20 23 4 17 39 56 33 46 35 18 21 10 48 53 40 57 24 11 16 5 59 32 45 52 41 26 9 12 44 49 58 25 62 15 6 27 31 60 51 42 29 8 13 64 50 43 30 61 14 63 28 7
Check the image below before we explain the code:
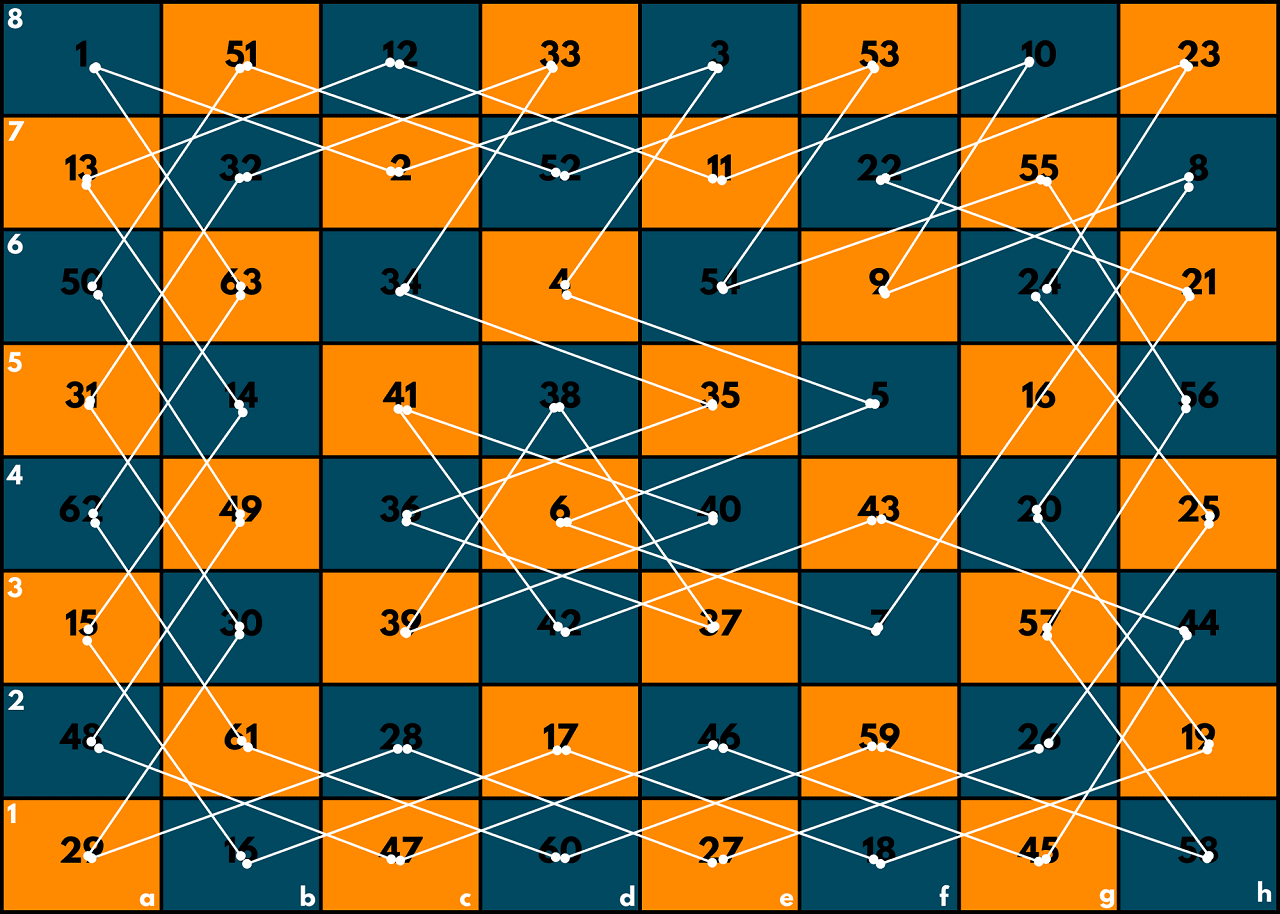
In this implementation, we first define a function validMoves which takes the current row and column of the knight as input and returns a vector of pairs representing all the valid moves that the knight can make from that position.
The solve function is a recursive function that takes the current row and column of the knight, as well as the current move number, as input. We mark the current square as visited by setting board[row][column] it to the current move number, and then we recursively try all possible moves from the current position.
If we reach the last move, then we found a solution and return true. If no valid move is found from the current position, we backtrack by setting the current square to 0 and returning false.
In the main function, we start the solve function at a specified starting position and then output the number of moves it took to find a solution and print the final chessboard with the solution.
Time & Space Complexity for Backtracking
The backtracking algorithm used to solve the Knight's Tour problem has an exponential time complexity. The number of possible paths for the knight grows very quickly as the size of the chessboard increases, which means that the time taken to explore all possible paths grows exponentially.
The exact time complexity of the Knight's Tour Backtracking algorithm is O(8^(n^2)), where n is the size of the chessboard. This is because each move has a maximum of 8 possible directions, and we have to explore all possible moves until we find a solution.
The space complexity of the backtracking algorithm is O(n^2), where n is the size of the chessboard. So, we can say that the backtracking algorithm is efficient for smaller chessboards.
Warnsdorff's Rule
Warndorff's rule is a heuristic greedy algorithm used to solve this problem. It tries to move the knight to the square with the fewest valid moves, hoping that this will lead to a solution.
Here's an overview of how Warndorff's rule algorithm works:
- Start with a random square on the chessboard.
- From the current square, consider all possible moves and count the number of valid moves from each adjacent square.
- Move to the square with the lowest number of valid moves. In case of a tie, move to the square with the lowest number of valid moves from its adjacent squares.
- Repeat steps 2 and 3 until all squares on the chessboard have been visited.
Here is the pseudocode for Warndorff's rule algorithm:
initialize the chessboard choose a random starting square while there are unvisited squares: mark the current square as visited for each adjacent square to the current square: count the number of valid moves from that square move to the adjacent square with the lowest count
The time complexity of Warndorff's rule algorithm is O(n^2 log n), where n is the size of the chessboard. This is because we have to visit each square once, and for each square, we have to compute the number of valid moves from each adjacent square. The space complexity of the algorithm is O(n^2) since we need to store the chessboard and the current position of the knight.
Overall, The Knight's Tour problem is related to chess, and solving it can help chess players improve their strategy and become better at the game. In the real world, you can also use it to design efficient algorithms for finding the shortest path between two points in a network.
Conclusion
Now we know The Knight's Tour Problem and its solutions using Backtracking and Warnsdorff's Rule. It has several applications in various fields such as Game theory, Network Routing etc, making it an important problem to study in computer science and mathematics.








