In this article, we will study what is kadane’s algorithm and its problem-solving property to solve the “Maximum Subarray Sum” problem. We will go through the algorithm and python code for the same along with the example and its corresponding output. Lastly, we will study the time complexity of the algorithm and the real-life application of kadane’s algorithm. So, let’s get started!
What is Kadane’s Algorithm?
Kadane’s algorithm is one of the famous approaches to solve the problem using dynamic programming. As we all know, the maximum subarray problem is one of the famous problems in the field of dynamic programming. You must be thinking that the problem seems to be easy and the result of the problem will be the sum of all elements in an array. But this is not correct. There will be negative integer elements in the array that can decrease the sum of the entire array. Therefore, to solve this problem, we will use the kadane’s algorithm.
Here the algorithm will find the continuous subarray in the 1D integer array which has the largest sum possible. The first approach for everyone after understanding the problem statement will be applying the brute-force approach and solving the problem. But by doing so, the time complexity of the solution will be O(n2) which is not very good. Therefore, we will apply the kadane’s algorithm which solves the problem by traversing over the whole array using two variables to track the sum so far and maximum total. The most important thing to pay attention to while using this algorithm is the condition using which we will update both variables.
Algorithm for Maximum Subarray Sum:
- Initializing max_till_now = 0
- Initializing max_ending = 0
- Repeat steps 4 to 6 for every element in the array
- Set max_ending = max_ending + a[i]
- if (max_ending<0) then set max_ending = 0
- if (max_till_now < max_ending) then set max_till_now = max_ending
- return max_till_now
In the above algorithm, max_ending is used to look for all the positive elements of the array, and max_till_now is used to look for the maximum sum of elements among all positive segments. Therefore, each time we get the positive-sum while comparing with max_till_now, we will update it with the greater sum.
Therefore, when the max_ending becomes negative, we set it to zero, and at each iteration, we check for max_till_now < max_ending to update max_till_now if the condition returns true.
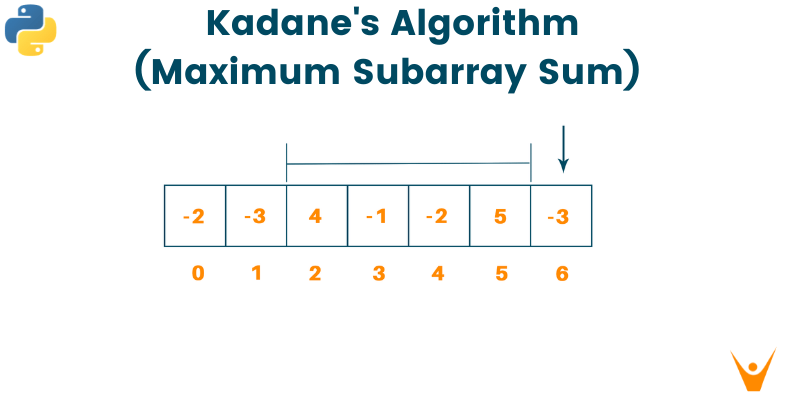
Example
Consider the following integer array:

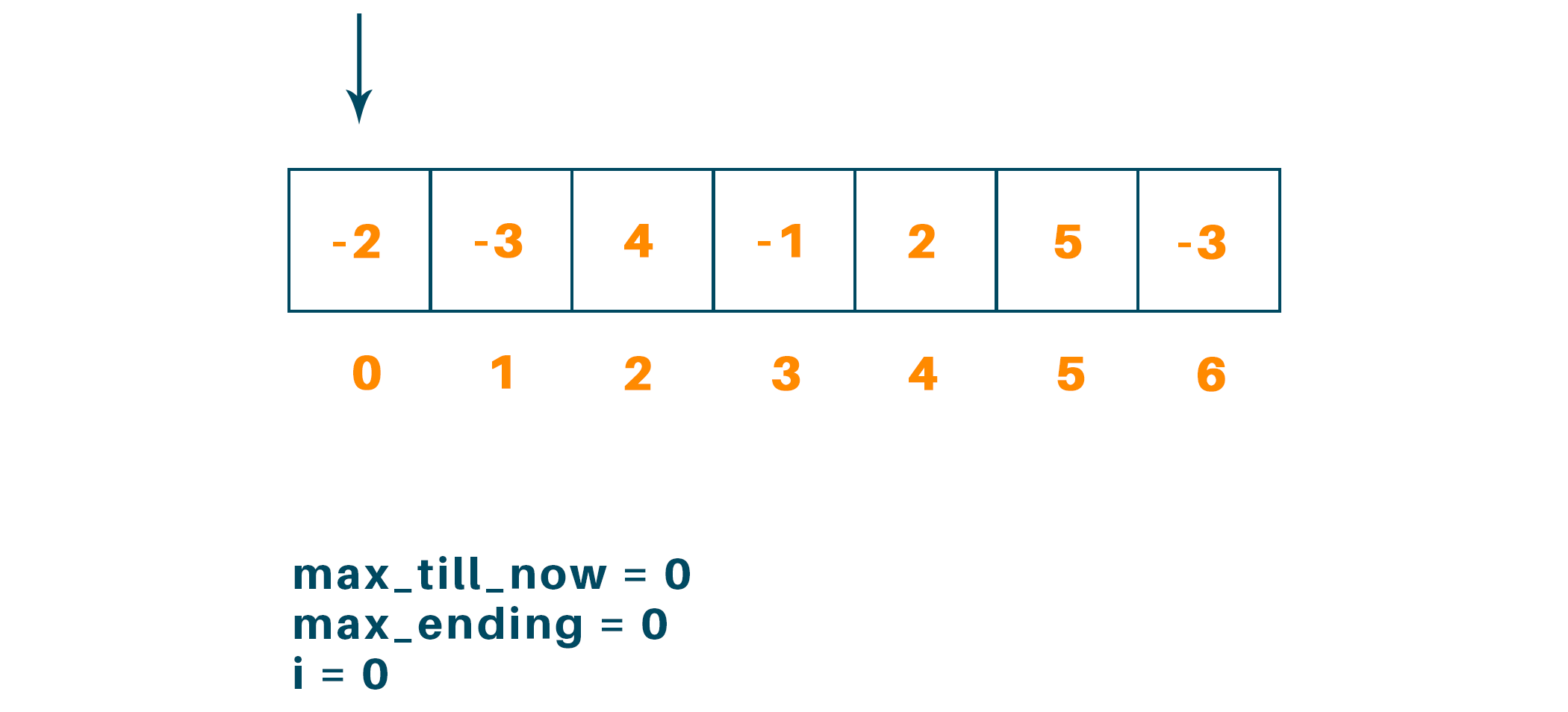
Initializing max_till_now = 0 and max_ending = 0 (i = 0)
Now, for i = 1 we get max_till_now = 0 and max_ending = 0 but for i = 2 max_till_now = 4 and max_ending = 4
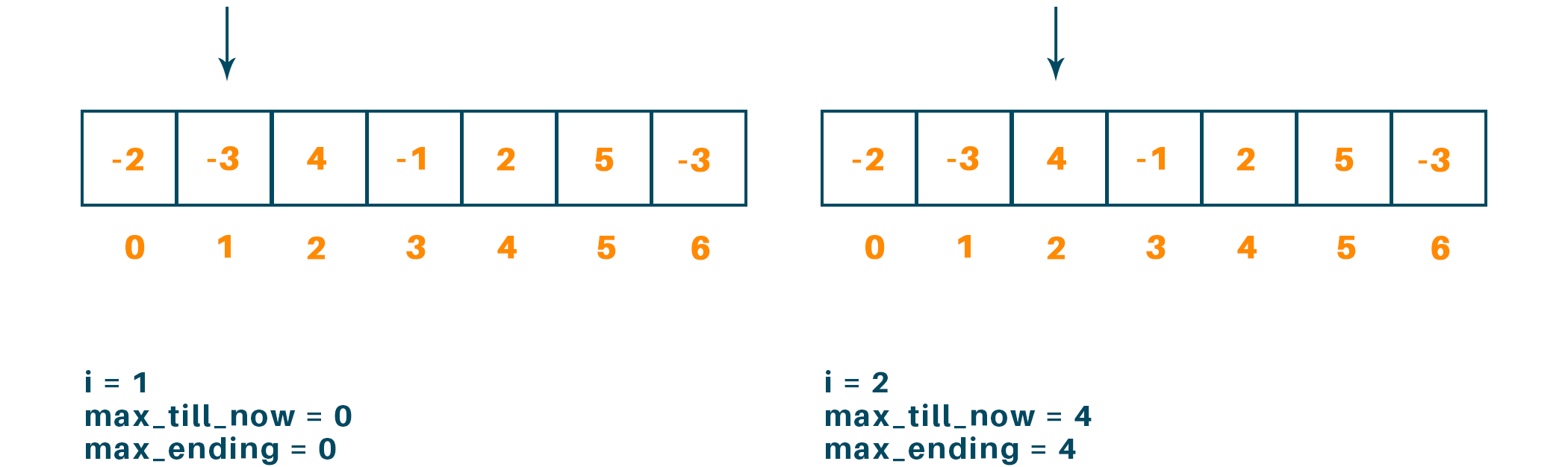
Now i = 3, i = 4, we get max_till_now = 4 and max_ending = 3, max_till_now = 4 and max_ending = 1 respectively.
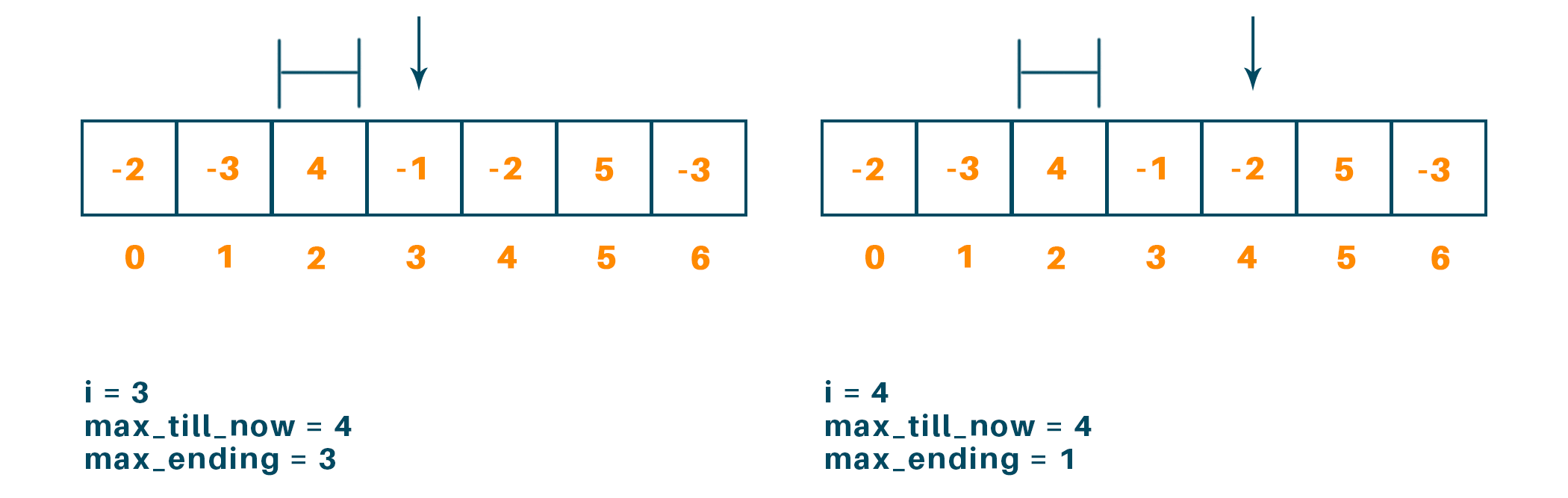
Now when i = 5 we get max_till_now = 6 (6>4) and max_ending = 6
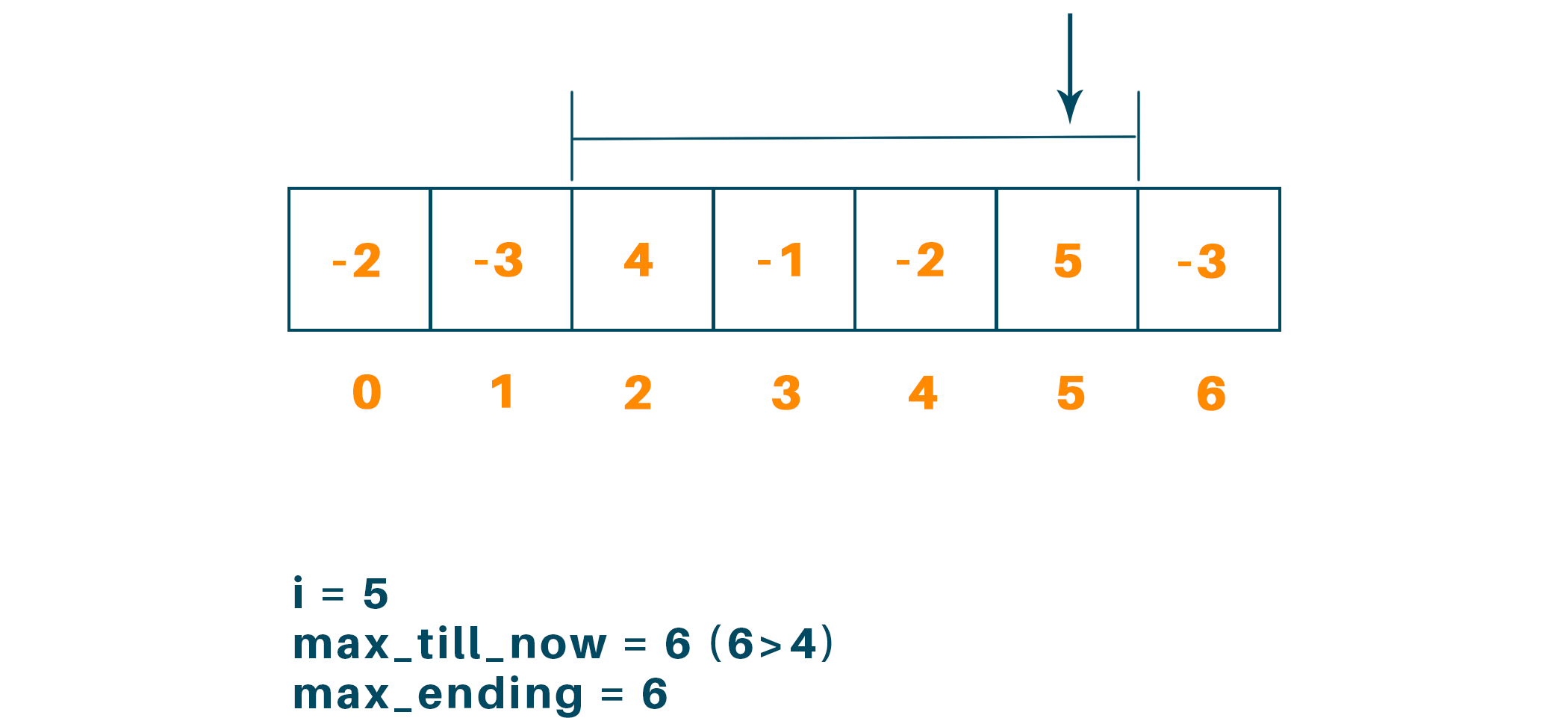
And when i = 6 we get max_till_now = 6 and max_ending = 3
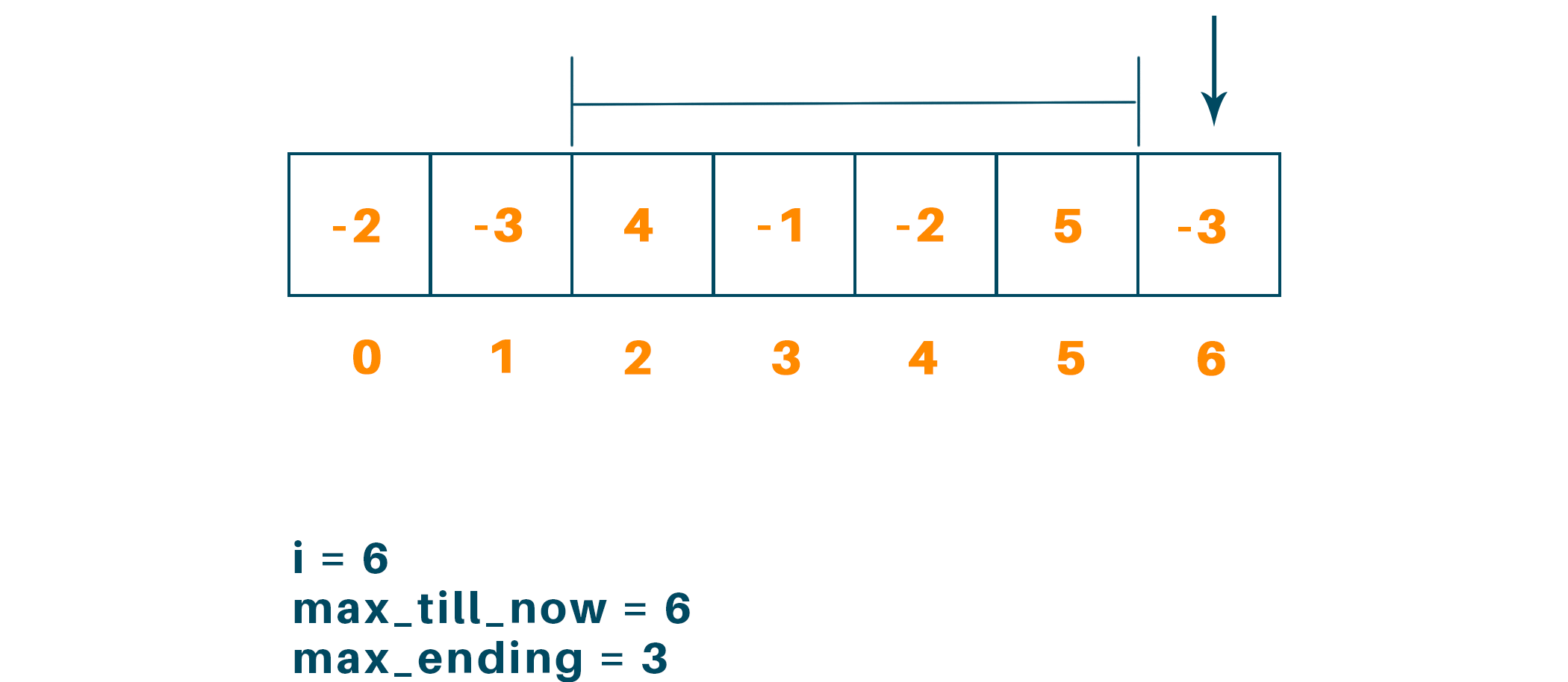
Therefore, from the above example, we get to find the maximum subarray is from i = 2 to i = 5 and the maximum sum is 6.
Python Code For Kadane’s Algorithm:
Below is the python code for kadane’s algorithm:
def maxSubArraySum(arr,size): max_till_now = arr[0] max_ending = 0 for i in range(0, size): max_ending = max_ending + arr[i] if max_ending < 0: max_ending = 0 elif (max_till_now < max_ending): max_till_now = max_ending return max_till_now arr = [-2, -3, 4, -1, -2, 5, -3] print("Maximum Sub Array Sum Is" , maxSubArraySum(arr,len(arr)))
Output
The output of the above code will be as given below:
Maximum Sub Array Sum Is 6
Time Complexity
The time complexity of kadane’s algorithm for an array containing n integer element is O(n) as only one for loop is to be executed throughout the program. Similarly, the auxiliary space complexity of the algorithm is O(1).
Applications
There are many applications of kadane’s algorithm and some of them are as mentioned below:
- Finding maximum subarray sum for a given array of integer
- Used as an image processing algorithm
- It can be used to solve the problems like “Station Travel in Order” and “Hotels Along the Coast”
- It is used for business analysis
Conclusion
Therefore, from the problem statement of finding the maximum subarray sum, the solution doesn’t seem to be this easy but using kadane’s algorithm we simplified it and achieved the solution with the least time complexity. This was possible because kadane’s algorithm uses the technique to gather the information which is required to reach the solution avoiding unnecessary storage of data and hence, this algorithm can be considered as a simple example of a dynamic programming approach with lots of practical application in the real world.