Find Peak Element (With Java and Python Code)

We are back with yet another competitive coding problem. Till now you must be aware of how important these problems are to get your dream job, as most companies like to assess their problem-solving skills. One way to do so is by giving them some variations of some major competitive problems. In this article, we are going to discuss a problem called “Find peak element”. We also discuss the naïve and efficient approach to solving this problem along with the code and time complexities.

Problem Statement

Before jumping straight to the approach, we must know what the problem is. So, let's discuss the problem.

The problem states that we are given an array of numbers and we are required to find a peak element from it.

Now, what is a peak element? A peak element is that number in the given array which is greater than its neighboring elements. And for an end element to be the peak element it just needs to be greater than the element before or after it.

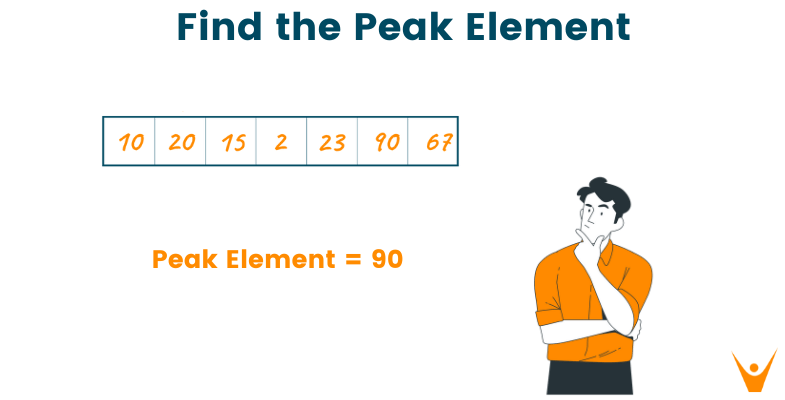
Let us take an example to illustrate this better. Suppose we are given the array arr that contains values as follows:
Arr= {10, 20, 15, 2, 23, 90, 67}

In this array, the peak element can be either 20 or 90. Why? because the neighbors of both the elements (10, 15 in case of 20 and 23, 67 in case of 90) are smaller than the element itself.

In some special cases, like if the array is sorted in ascending order. Then, the last element of the array is the peak element. However, if the array is sorted in descending order then the first element is the peak element.

Naive Approach

The first solution that might come into your mind is that we can traverse through the array from the second element to the second last element. And for each element, we can check the element before and after it. And if both the elements are smaller than the current element then congratulations, we have our peak element. But before traversing the whole array we need to rule out the possibility of the first and last element being the peak element. To do this, we need to check the value of the second element and if this value is greater than the first element then the first element is the peak element. The same is done for the last element except for the second element we check the value of the second last element.

Now, this approach works very well and achieves the task we are aiming for. But it has a time complexity of O(n), since all the elements need to be traversed once in the worst case, and we have a more efficient approach available to solve this.

Using Modified Binary Search

We employ a modified concept of binary search to solve this problem more efficiently. We suggest you go through the binary search article before continuing. However, if you are already familiar with it then you can continue.

In this approach, we check the value of the middle element with its neighboring elements. If it is greater then we have found the peak element and return it. If this is not the case, then we check the value of the element left to the middle value. If the left value is greater than the middle value then the peak element must be present on the left side. This algorithm is then called recursively on the left side of the array.

However, if the left element is smaller then the right element is checked. If the value of the right element is greater than the middle element then the algorithm is recursively called on the left side of the array. This process is continued until we find a peak element or the lowerbound is smaller than the upperbound.

Algorithm

Let us now discuss the algorithm of this approach.

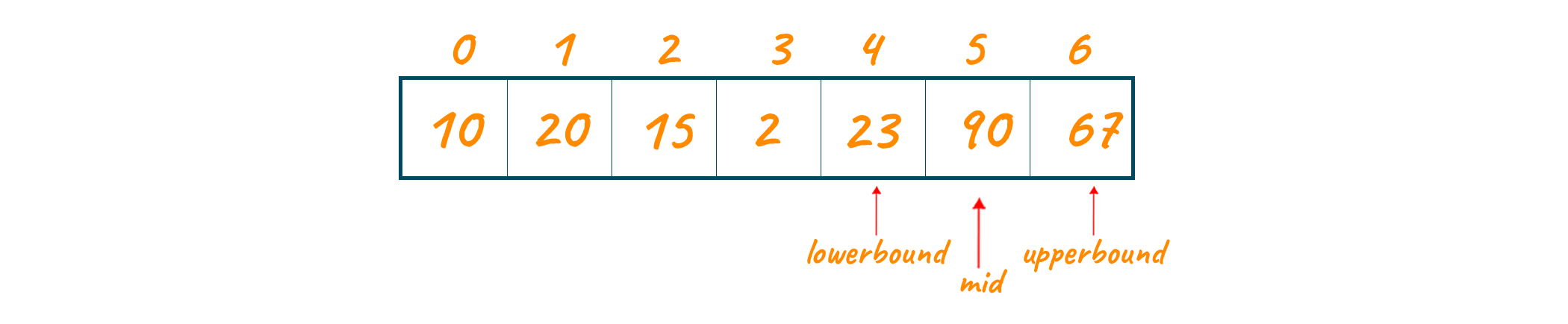
1 Create two variables, LowerBound and UpperBound, and set them to 0 and n-1, respectively.
2. Iterate the steps below until the lowerbound is less than the upperbound and LowerBound = UpperBound.
3. Check whether the mid-value or index mid = (LowerBound+UpperBound)/2, is the peak element; if it is, print the element and exit the loop.
4. Otherwise, if the element on the right side of the middle element is larger, look for the peak element on the right side, i.e. update LowerBound = mid + 1.
5. Otherwise, if the element on the left side of the middle element is greater, look for the peak element on the left, i.e. update UpperBound = mid – 1.

How to Find Peak Element in Array?

In the first recursion since the mid element is smaller than its neighboring elements, therefore, it cannot be the peak element. The element of the right to the mid is checked, and since its value is greater than the mid element, that is why we continue to check for the peak element on the right side of the array. The LowerBound variable is made to store the mid+1 index i.e. 4.

In the second recursive call, the element at the mid index is 90 and since it is greater than both of its neighboring elements, it is returned and we get our answer as 90.

Java Code for Finding Peak Element

public class findPeakElement {

    private static int findPeakUtil(int[] arr,int low,int high,int n){

        //finding the middle element of array
        //this method is more reliable
        int mid=low+(high-low)/2;

        //Compare middle element with its neighbours
        if((mid==0 || arr[mid-1]<=arr[mid]) && (mid==n-1 || arr[mid+1]<=arr[mid]))
            return mid;

        // If middle element is not peak and its
        // left neighbour is greater than it,
        // then left half must have a peak element
        else if(mid>0 && arr[mid-1]>arr[mid])
            return findPeakUtil(arr,low,(mid-1),n);
        // Similarly,if the middle element is not the peak and
        // its right side element is greater than it,
        // then right half must have a peak
        else
            return findPeakUtil(arr,(mid+1),high,n);
    }

    public static void main(String[] args) {
        int[] arr={10,20,15,2,23,90,67};
        int n=arr.length;
        System.out.println("The peak point is "+arr[findPeakUtil(arr,0,n-1,n)]);
    }

}

Python Code for Finding Peak Element

def findPeakUtil(arr, lowerBound, upperBound, n):
	
    # Find the middle index
	mid = lowerBound + (upperBound - lowerBound)/2
	mid = int(mid)
	
	# Compare middle element with its
	# neighbours
	if ((mid == 0 or arr[mid - 1] <= arr[mid]) and
		(mid == n - 1 or arr[mid + 1] <= arr[mid])):
		return mid


	elif (mid > 0 and arr[mid + 1] > arr[mid]):
		return findPeakUtil(arr, (mid + 1), upperBound, n)

	else:
		return findPeakUtil(arr, lowerBound, (mid - 1), n)


arr = [10, 20, 15, 2, 23, 90, 67]
n = len(arr)
print("The peak point is", arr[findPeakUtil(arr, 0, n - 1, n)])

Output:

The peak point is 90

Time Complexity 

This approach has a time complexity of O( log n) because at each step the size of the array becomes half. You can also compare it with the binary search technique to understand it better.

Space Complexity

Since this algorithm employs no extra space therefore its space complexity is O(1).

Takeaway

In this article, we discussed how to find the peak element in an array along with its java and python code. While solving such type of problems it is necessary to understand that just solving them is not the key but solving them efficiently is.