Find Equilibrium Index of an Array (with code)

An array is a basic data structure in computer science that is used to hold a group of identically typed components. One interesting property of an array is the existence of an equilibrium index. In this article, we will discuss the Equilibrium Index of an array, and how to find it efficiently.

What is the Equilibrium Index of an Array?

As we know, the array is a collection of elements where each element has an index that tells us the position of it in the array.

The index at which the sum total of the items on the left side of the array equals the sum of the elements on the right side of the array is known as the equilibrium index.

Mathematically, if an array A has n elements, then the equilibrium index i is defined as follows:

A[0] + A[1] + ... + A[i-1] = A[i+1] + A[i+2] + ... + A[n-1]

Note that the sum of the elements at the equilibrium index i is not included in either side of the equation. An array can have multiple equilibrium indices or none at all. If there are multiple equilibrium indices, we only need to find one of them.

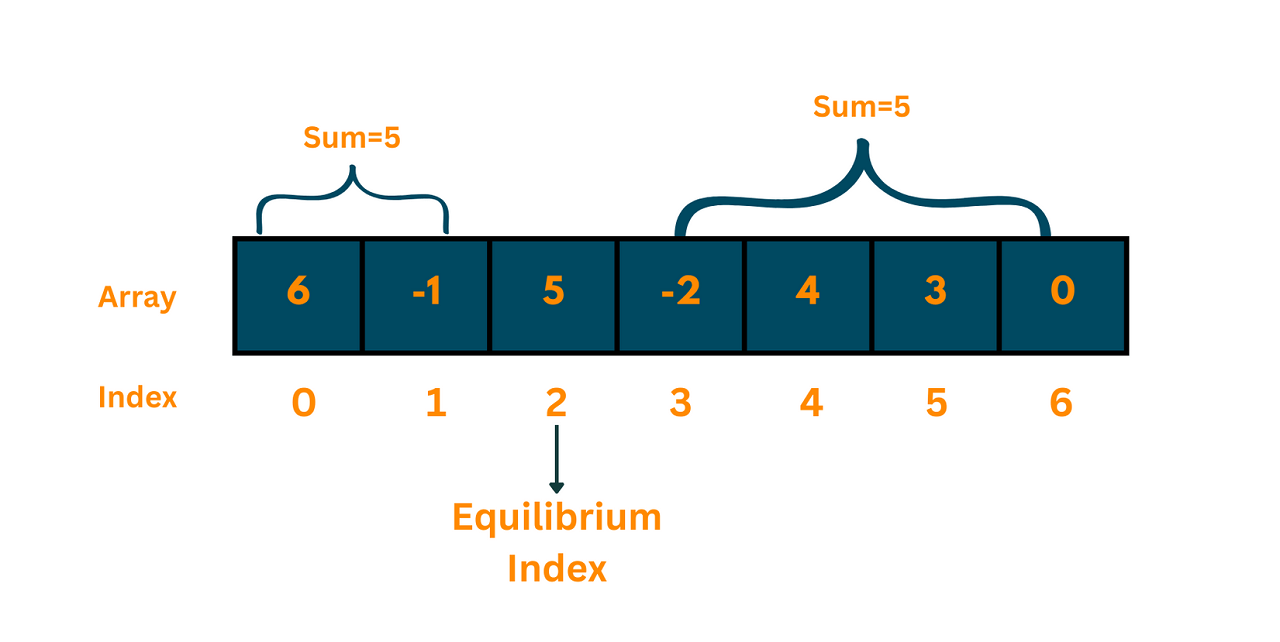
For example,  Let's consider the following array:

arr = [6, -1, 5, -2, 4, 3, 0]

The equilibrium index in the above array is 2.

Why is the Equilibrium Index Important?

Finding the equilibrium index of an array can be useful in various applications, such as finding the center of mass in a physical system, or optimizing the performance of an algorithm by partitioning data into two roughly equal parts.

For example, in the stock market, we can use the equilibrium index to identify a point in time where the supply and demand of a particular stock are balanced and make an informed decision about buying or selling that stock.

Algorithm to Find Equilibrium Index

We can find the equilibrium index of an array by iterating through the array and calculating the left and right sums at each index. However, this method has a time complexity of O(n^2), where n is the number of elements in the array because we need to calculate the sum for each index.

To improve efficiency, we can use a cumulative sum approach. We first calculate the cumulative sum of the array from left to right and store it in a new array. Then, we iterate through the original array from right to left and calculate the right sum at each index.

Finally, we compare the left sum and right sum at each index to find the equilibrium index. This method has a time complexity of O(n), because we only need to iterate through the array twice.

Here is an algorithm to find the equilibrium index of an array without using cumulative sum:

1. Initialize two variables, left_sum, and right_sum, to 0.
2. Calculate the total sum of the array and store it in a variable total_sum.
3. Loop through each element of the array:
   1. Subtract the current element from total_sum to get the right_sum.
   2. Check if left_sum is equal to right_sum. If they are equal, return the current index as the equilibrium index.
   3. Add the current element to left_sum.
4. If no equilibrium index is found, return -1.

Before we implement it, let's understand the logic and the pseudocode of the given problem: 

function equilibriumIndex(arr):
    left_sum = 0
    right_sum = 0
    
    # Calculate the total sum of the array
    total_sum = sum(arr)
    
    # Loop through each element of the array
    for i in range(len(arr)):
        # Subtract the current element from the total sum to get the right sum
        right_sum = total_sum - left_sum - arr[i]
        
        # Check if the left and right sums are equal
        if left_sum == right_sum:
            return i
        
        # Add the current element to the left sum
        left_sum += arr[i]
    
    # If no equilibrium index is found, return -1
    return -1

The idea behind this algorithm is to calculate the total sum of the array and then loop through each element of the array, keeping track of the left sum and the right sum.

At each iteration, we subtract the current element from the total sum to get the right sum and then check if the left and right sums are equal. If they are, we return the current index as the equilibrium index. If no equilibrium index is found, we return -1.

C++ Program to Find Equilibrium Index

Below is the full C++ code to find equilibrium index in an array:

#include 
#include 

using namespace std;

int equilibriumIndex(vector<int> arr) {
    int n = arr.size();
    int leftSum = 0, rightSum = 0;

    // Calculate sum of all elements in the array
    for (int i = 0; i < n; i++) {
        rightSum += arr[i];
    }

    // Iterate through the array and find equilibrium index
    for (int i = 0; i < n; i++) {
        // Subtract current element from right sum
        rightSum -= arr[i];

        // Check if left sum is equal to right sum
        if (leftSum == rightSum) {
            return i;
        }

        // Add current element to left sum
        leftSum += arr[i];
    }

    // Equilibrium index not found
    return -1;
}

int main() {
    vector<int> arr = {6, -1, 5, -2, 4, 3, 0};
    int index = equilibriumIndex(arr);

    if (index == -1) {
        cout << "No equilibrium index found\n";
    } else {
        cout << "Equilibrium index found at position " << index << "\n";
    }

    return 0;
}

Output:

Equilibrium index found at position 2

In this approach, we first calculate the sum of all elements in the array. Then, we iterate through the array from left to right and subtract the current element from the right sum, and add it to the left sum. If the left sum is equal to the right sum, we have found an equilibrium index.

The time complexity of finding the equilibrium index of an array using the two-pointer approach is O(n), where n is the size of the array. This is because we need to iterate over the array twice - once to calculate the total sum of the array and once to find the equilibrium index. Both iterations take O(n) time.

#include 
#include 
using namespace std;

int equilibriumIndex(vector<int>& arr) {
    int n = arr.size();

    // Calculate prefix sum
    vector<int> prefixSum(n, 0);
    prefixSum[0] = arr[0];
    for (int i = 1; i < n; i++) {
        prefixSum[i] = prefixSum[i-1] + arr[i];
    }

    // Calculate suffix sum
    vector<int> suffixSum(n, 0);
    suffixSum[n-1] = arr[n-1];
    for (int i = n-2; i >= 0; i--) {
        suffixSum[i] = suffixSum[i+1] + arr[i];
    }

    // Find equilibrium index
    for (int i = 0; i < n; i++) {
        if (prefixSum[i] == suffixSum[i]) {
            return i;
        }
    }

    // Equilibrium index not found
    return -1;
}

int main() {
    vector<int> arr = {6, -1, 5, -2, 4, 3, 0};
    int index = equilibriumIndex(arr);

    if (index == -1) {
        cout << "No equilibrium index found" << endl;
    } else {
        cout << "Equilibrium index found at position " << index << endl;
    }

    return 0;
}

Output:

Equilibrium index found at position 2

This code uses prefix sum to calculate the sum of all elements up to each index in the array, and suffix sum to calculate the sum of all elements after each index in the array. Then, it checks each index to see if its prefix sum is equal to its suffix sum and returns the first index that satisfies this condition. If no equilibrium index is found, the function returns -1.

The time complexity of finding the equilibrium index of an array using the prefix sum is O(n), where n is the size of the array. This is because we need to iterate over the array twice to calculate the prefix sum and suffix sum, which takes O(n) time, and then iterate over the array once more to find the equilibrium index, which also takes O(n) time in the worst case.

The space complexity of this approach is also O(n), as we need to store two additional arrays of size n to calculate the prefix sum and suffix sum.

Conclusion

So, basically, the equilibrium index is where the total of the items to its left and right, which are of the same data type, equals the sum of the elements to its right. Still confused? Our C++ homework help online is always open for you.