Binary trees are an essential data structure in computer science and traversing it means visiting each node exactly once in a specific order. In this article, we will explore diagonal traversal in a binary tree using C++.
What is Diagonal Traversal?
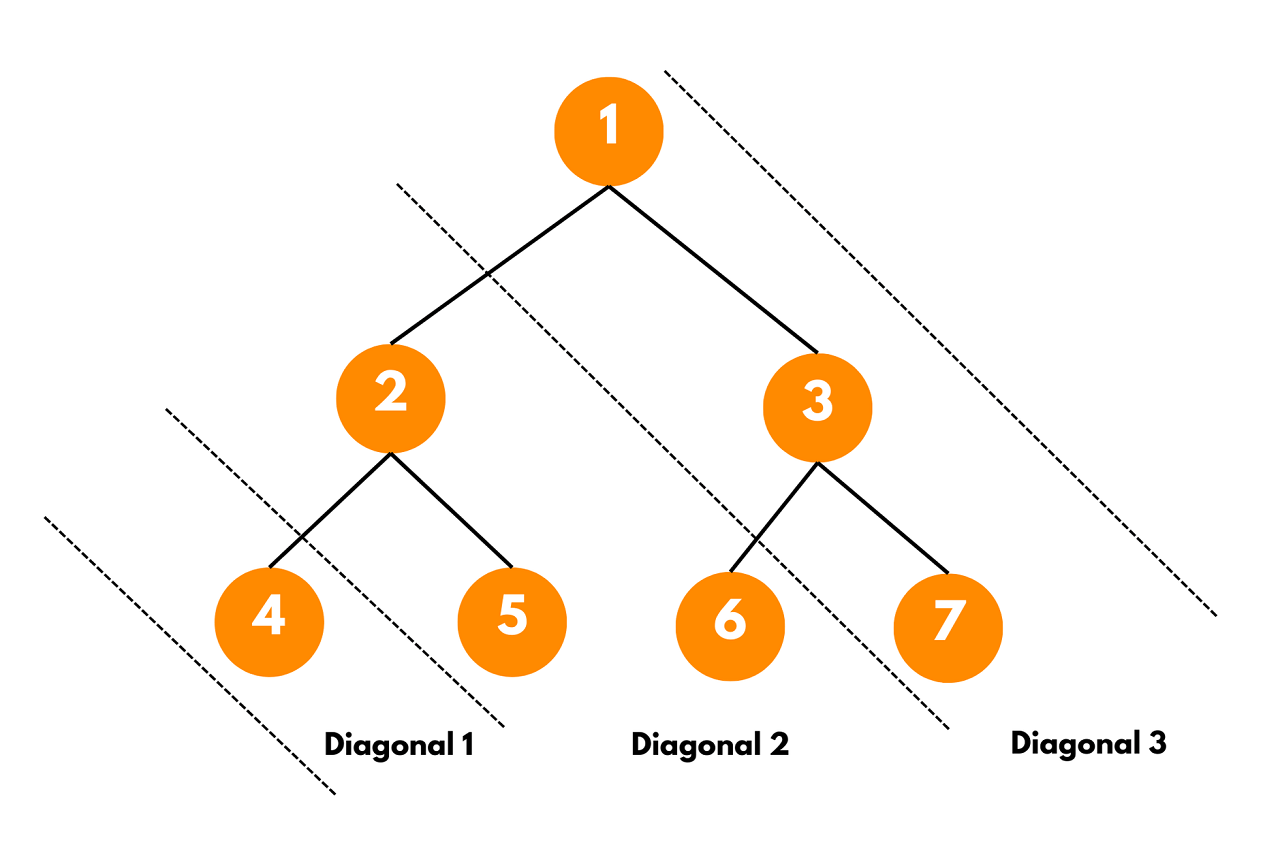
The diagonal traversal of a binary tree is a unique way of visiting its nodes. Unlike traditional traversal methods like pre-order, in-order, or post-order, which follow strict left-to-right or right-to-left approaches, diagonal traversal moves along the diagonals of the tree.
It means that at each step, we visit the left child (if it exists) before moving to the right child. The traversal moves diagonally from the root towards the bottom-right of the tree.
This unique traversal approach can be useful in specific scenarios, such as printing elements of a matrix stored in a binary tree or performing certain operations on nodes based on their diagonal positions in the tree.
The diagonal traversal algorithm can be best understood through an example. Consider the following binary tree:
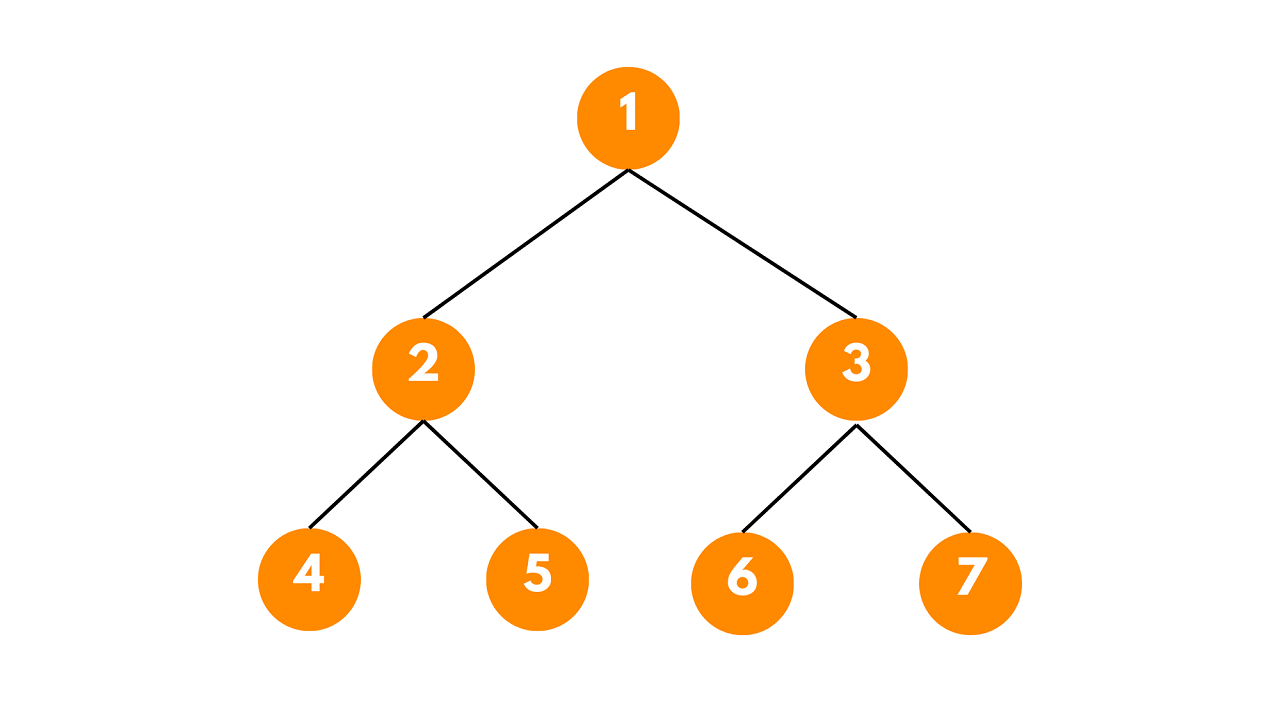
The diagonal traversal of this tree will be: 1 -> 3 -> 7 -> 2 -> 5 -> 6 -> 4
C++ Implementation
To perform diagonal traversal of a binary tree, we can use a modified version of depth-first search (DFS) that tracks the diagonal level and stores nodes in a map. The map is used to group nodes belonging to the same diagonal level.
Here is the C++ code to traverse a binary tree diagonally:
#include <iostream> #include <vector> #include <map> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; void diagonalTraversalHelper(TreeNode* root, int diagonalLevel, map<int, vector<int>>& diagonalMap) { if (!root) return; diagonalMap[diagonalLevel].push_back(root->val); diagonalTraversalHelper(root->left, diagonalLevel + 1, diagonalMap); diagonalTraversalHelper(root->right, diagonalLevel, diagonalMap); } vector<int> diagonalTraversal(TreeNode* root) { map<int, vector<int>> diagonalMap; diagonalTraversalHelper(root, 0, diagonalMap); vector<int> diagonalTraversalResult; for (const auto& it : diagonalMap) { for (const auto& val : it.second) { diagonalTraversalResult.push_back(val); } } return diagonalTraversalResult; } int main() { // Build the binary tree as shown in the example TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); vector<int> diagonalResult = diagonalTraversal(root); // Print the diagonal traversal result for (int val : diagonalResult) { cout << val << " "; } cout << endl; return 0; }
Output:
1 3 7 2 5 6 4
Time and Space Complexity
The time complexity of the provided diagonal traversal code is O(N), where N is the number of nodes in the binary tree. In the worst case, we need to visit all nodes once to perform the traversal. The space complexity of the code is O(N), where N is the number of nodes in the binary tree.
Diagonal Sum of a Binary Tree
The diagonal sum of a binary tree is the sum of all nodes that lie on the same diagonal line. A diagonal line starts from the root of the tree and moves down and to the right, crossing through the left and right subtrees along the way. At each level of the binary tree, nodes with the same diagonal distance from the root are added together to compute the diagonal sum.
To compute the diagonal sum of a binary tree, we can perform a depth-first traversal (DFS) while maintaining the diagonal distance of each node from the root. During the traversal, we keep a mapping of diagonal distances to their respective sums. For each node, we update the sum of the corresponding diagonal distance in the mapping and pass it to its children for further processing.
Here is the C++ code to find the diagonal sum of a binary tree:
#include <iostream> #include <map> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; void diagonalSumHelper(TreeNode* root, int diagonalDistance, map<int, int>& diagonalSumMap) { if (!root) return; // Update the diagonal sum for the current diagonal distance diagonalSumMap[diagonalDistance] += root->val; // Recur for the left and right subtrees with the updated diagonal distance diagonalSumHelper(root->left, diagonalDistance + 1, diagonalSumMap); diagonalSumHelper(root->right, diagonalDistance, diagonalSumMap); } map<int, int> diagonalSum(TreeNode* root) { map<int, int> diagonalSumMap; diagonalSumHelper(root, 0, diagonalSumMap); return diagonalSumMap; } int main() { // Build the binary tree as shown in the example TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); // Compute the diagonal sum of the binary tree map<int, int> diagonalSums = diagonalSum(root); // Print the diagonal sums cout << "Diagonal Sums:\n"; for (const auto& it : diagonalSums) { cout << "Diagonal " << it.first << ": " << it.second << "\n"; } return 0; }
Output:
Diagonal Sums: Diagonal 0: 11 Diagonal 1: 13 Diagonal 2: 4
The time complexity of the provided diagonal sum code for a binary tree is O(N), where N is the number of nodes in the binary tree.
Conclusion
Overall now we covered everything you need to know about this topic. The diagonal traversal follows the diagonals of the binary tree from the top-left to the bottom-right, visiting nodes at each diagonal level before moving on to the next diagonal.








